卸荷煤体分数阶渗透率模型参数探讨及其在渗流模拟中的应用

赵家巍，周宏伟，刘泽霖，谢森林，赵文慧，钟江城，5，史艳楠，王毅颖

(1.中国矿业大学(北京)力学与建筑工程学院，北京 100083；2.中国矿业大学(北京)能源与矿业学院，北京 100083；3.煤炭资源与安全开采国家重点实验室，北京 100083；4.中国矿业大学(北京)应急管理与安全工程学院，北京 100083；5.临沂大学 土木工程与建筑学院，山东 临沂 276000；6.河北工程大学 机械与装备工程学院，河北 邯郸 056038)

目前煤炭开采深度已达1 500 m，并且仍在继续延深，未来深部资源开采将成为常态，在深部赋存环境下，煤岩体的力学行为呈现出强烈的非线性和不可逆特征，深部煤岩体非线性力学响应等许多问题难以采用传统的岩石力学理论来解释和描述。深部开采扰动造成煤岩体强烈卸荷，煤体内原生裂隙快速扩展，产生严重的损伤破坏，引起渗透率急剧变化。目前开采卸荷煤岩体的渗透率演化问题逐渐引起众多学者的关注，并从不同角度分别建立了由体积应变表征和有效应力表征的两大类渗透率模型。

由体积应变表征的渗透率模型以KOZENY-CARMAN方程为基础，如谢和平等在综合考虑支承压力、孔隙压力和瓦斯吸附膨胀耦合作用的基础上，推导得出了煤体增透率表达式；程远平等在建立了考虑有效应力和瓦斯吸附解吸变形等因素的、以应变为变量的煤体卸荷损伤增透理论模型；荣腾龙等通过引入了内膨胀应变系数的概念，基于DRUCKER-PRAGER破坏准则，建立了考虑煤体损伤破裂的渗透率演化模型；ZHANG等在等效应变的框架下建立了双重孔隙介质各向同性损伤本构方程，采用标量损伤变量的概念，开发出渗透演化的动态模型。

由有效应力表征的渗透率模型以SHI-DURUCAN模型为基础，如杨天鸿等通过引入煤体变形过程中应力、损伤与渗透性演化的耦合作用方程，建立了渗流-应力渗透率模型，并据此分析了深部采动影响下瓦斯抽采过程中煤层渗透性的演化和抽采孔周围瓦斯压力的变化规律；薛熠等通过对峰前和峰后渗透率进行分段表达，在峰后阶段的模型中加入突变系数，结合煤体有效偏应力的变化，建立了峰后损伤煤体渗透率模型；张雷等基于CUI-BUSTIN模型(C-B模型)建立了平均有效应力作用下的渗透率演化模型；CHEN等利用改进的Logistic增长函数，建立了渗透率从弹性状态到破坏后状态变化的模型，提出的渗透率模型是关于控制煤体压缩的平均有效应力和控制煤体破裂的有效偏应力的函数。

另外，还有一类模型是从宏-细观双尺度关联研究的角度建立的，此类模型将细观力学与断裂力学相结合，考虑裂纹扩展和各项异性特征，明确宏-细观变量之间的关系，建立起裂隙损伤渗透率模型，如SHAO、MALEKI、陆银龙等所做的工作。这类模型一般具有相对清晰的物理背景，能够触及到问题的本质，但其表达式往往过于复杂而不方便用于数值模拟和工程应用。

为了适应采动煤岩体非线性力学响应特征，在前述研究基础上，ZHOU等构建了分数阶渗透率模型，体现了损伤效应对煤体渗透性的影响作用，将经典S-D模型的适用范围拓展至峰后。笔者进一步对分数阶渗透率模型所引入的2个参数进行深入探讨，揭示其物理意义，并将分数阶渗透率模型应用于充填采动瓦斯流动规律的数值模拟中。

1 卸荷煤体应力-渗透率模型分析

从力学本质上讲，应力状态改变是煤体渗透率变化的原因，因此，考虑应力-渗流耦合作用的S-D模型更能从本质上描述煤体渗透率演化规律，该模型的表达式为负指数关系式：

=exp[-3(-)]

(1)

式中，为渗透率;为有效应力;下标0表示初始状态，MPa；为割理压缩系数，MPa，=1/-1/，其中为煤体裂隙的体积模量，MPa，为煤体的体积模量，MPa。

对式(1)两边取对数，并令=ln()，则式(1)可改写为

=-3(-)

(2)

可以看出，以煤层气抽采为背景建立的S-D渗透率模型，与Δ构成线性关系，是可以回退的弹性模型。但该模型无法反映采动卸荷煤体的渗透率变化，根据现有渗透率研究成果，将卸荷渗透率演化趋势绘制成如图1所示的概化模型。

由图1可知，在峰前阶段，煤体渗透率随有效应力增加而缓慢降低，峰后阶段产生损伤扩容，渗透性质发生改变，在强烈卸荷作用下煤体渗透率急剧增加。

图1 煤体卸荷渗透率演化概念模型[3]

为定量描述卸荷引起的渗透率变化，其中一个思路是通过引入透气系数增大倍率和应力敏感因子，得到渗流-应力耦合模型，将透气系数变换为渗透率后得到

(3)

其模型表征的渗透率变化曲线如图2所示(以瓦斯压力=5 MPa，有效应力系数=0.8为例)，通过设定不同的应力敏感系数和透气性增大系数来适应不同条件下开采扰动煤体应力释放引起的渗透性变化。

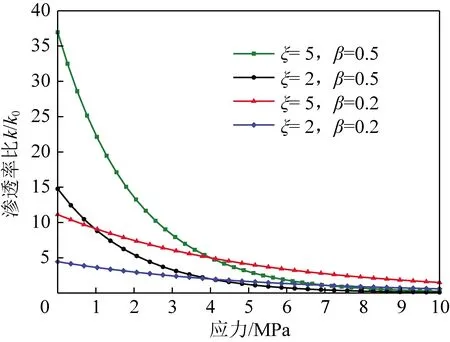
图2 不同ξ和β下渗透率比随应力变化分布

煤体峰后渗透率强烈变化的实质是卸荷导致煤体产生裂隙损伤，为此，有学者将损伤变量和突变系数嵌入S-D模型得到的渗透率模型为

(4)

其模型表征的渗透率变化曲线如图3所示(初始有效应力=40 MPa)，同样能够反映峰后渗透率的急剧变化。

图3 不同Cf和λD下渗透率比随应力变化分布

从唯象角度来看，原有的S-D模型表征的渗透率增大倍数有限，通过加入具有调节倍率功能的应力敏感因子或突变系数恰是释放了这种限度，从而得以在有关采动煤体瓦斯渗流的数值模拟和工程实践中应用。但是，从细观机理层面来看，现有应力-渗透率模型中的参数或替代参数所代表的煤体隔理压缩系数被设定为恒定值，即被视为不随力学过程变化的静态参数，与煤体损伤扩容、裂隙扩展过程中其割理压缩系数不断变化的事实不符，这也是S-D模型的适应性被局限在弹性阶段的原因。根据当前渗透率模型的发展趋势，考虑损伤变量的卸荷渗透率模型构建思路是可行的，但需要深入探讨新增参数与损伤变量之间的内在关系。

2 双/单参数分数阶渗透率模型

开采扰动煤体力学性质呈现出强烈的非线性特征，对此，在前述模型基础上进一步构建应力-损伤作用下的非线性渗透率模型。对于采动煤体，更多关注的是煤体峰后卸荷变形阶段的渗透率变化，为简化分析，假设损伤以应力峰值为起点，峰前与应力改变量Δ保持线性关系，峰后两者呈非线性关系。

构建非线性模型的方法有很多，而蕴含记忆效应或历史依赖性的分数阶导数模型具备独特优势，通过借鉴非达西渗流分数阶建模思想，文献[13]建立了满足上述条件的双参数分数阶渗透率模型：

=exp{[-(-)]1+(2+)}

(5)

式中，为与煤体割理压缩系数相关联的参数；为单位应力，MPa；为分数阶阶数；()为伽码函数。

该模型揭示了采动卸荷煤体的渗透率变化与应力之间的关系。分别以=05和=002为算例，借助Matlab计算程序可得出一组不同参数取值条件下渗透率的变化曲线(图4)。

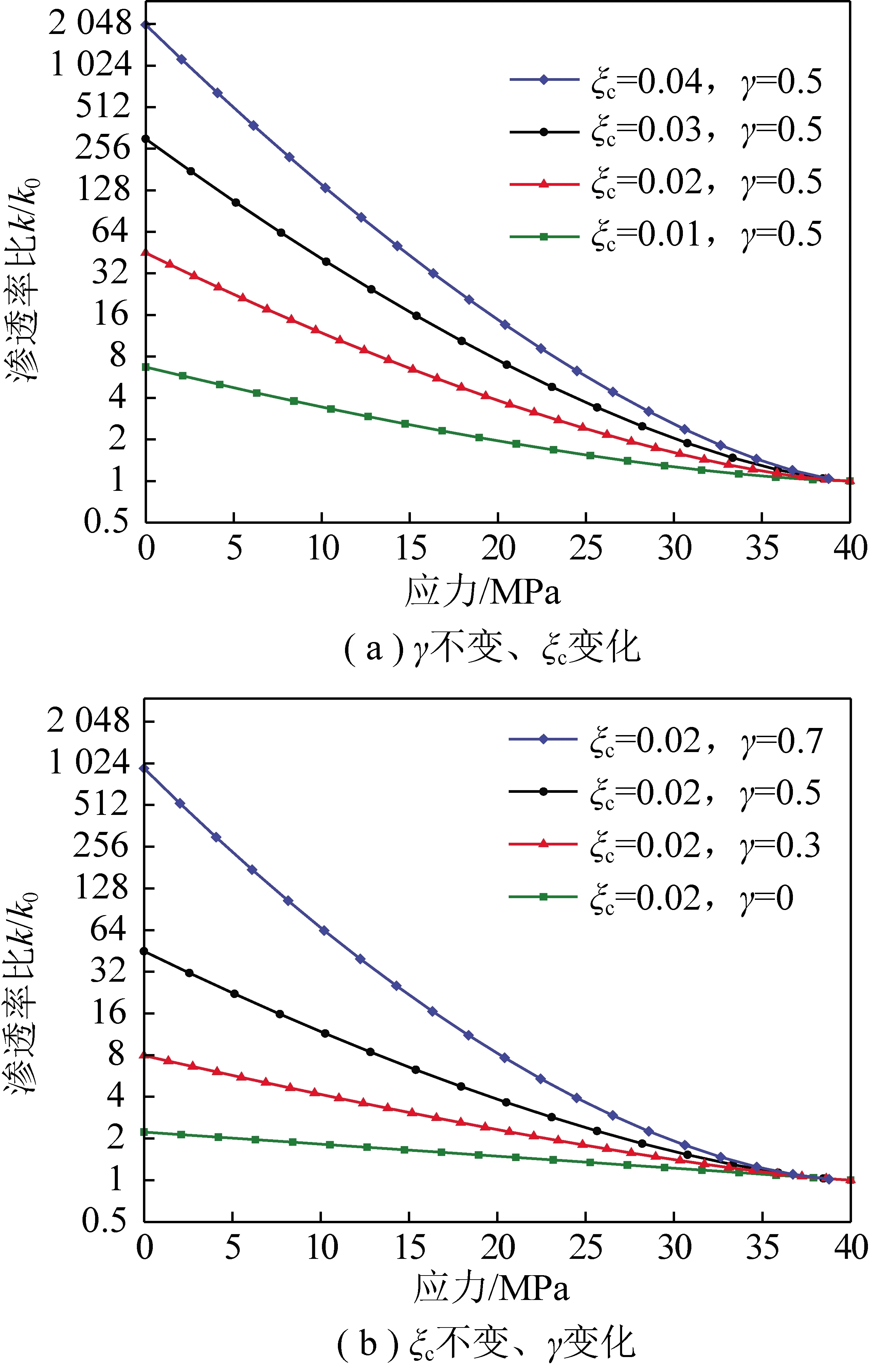
图4 不同参数下分数阶渗透率曲线

由图4可以看出，分数阶渗透率模型所描述的渗透率变化依赖于分数阶导数的阶数和割理压缩系数相关的，并且对2个参数的敏感度较高。特别地，当=0时，分数阶渗透率模型退化为经典的S-D模型，表明S-D模型是分数阶渗透率模型的一种特殊情形，=1时，分数阶渗透率模型表现为S-D模型的幂函数形式，展现峰后渗透率的强非线性变化特征。

2.1 模型验证与参数取值探讨

为验证所建立的卸荷煤体分数阶渗透率模型的有效性，利用课题组已进行的不同围压下煤岩试样的常规三轴压缩渗流试验的结果，进行拟合验证。试验煤块取自平煤12矿己-31030工作面(埋深992～1 118 m)，加工成尺寸为50 mm×100 mm的标准圆柱形煤样，利用MTS815岩石力学试验系统进行测试。

采用非线性最小二乘法，对分数阶渗透率模型和渗透试验数据进行拟合分析，确定相关参数，渗透率拟合结果如图5所示。

图5 分数阶渗透率模型验证结果

对于峰前阶段，由于假设煤体未产生损伤，=0，式(11)退回S-D模型，因此峰前采用S-D模型进行拟合，不再赘述。由图5可见，分数阶渗透率模型在峰后阶段的拟合效果非常好，3个围压条件下的确定系数均大于0.99，说明所建立的分数阶渗透率模型能够适应于卸荷煤体渗透率强烈非线性变化特征。

需要注意的是，模型中的是与煤体割理压缩系数相关联的参数，S-D模型之所以不能适应峰后渗透率的演化，正是由于在峰前阶段，煤的割理压缩系数是由其基本性质所确定的常数，而在峰后阶段，煤体产生损伤扩容而对割理压缩系数造成了影响。因此在确保渗透率模型有效的同时，还需要建立起和与损伤变量的关系。

为获得损伤变量的演化规律，需要构建损伤本构方程，在连续介质损伤力学中三维线弹性损伤本构方程可表示为

(6)

式中，为主应变;为切应变;为弹性模量;为泊松比;为主应力;为Kronecker符号。

由式(6)得到常规三轴加载路径下岩石的损伤本构方程

=2+(1-)

(7)

式中，为轴向应力;为围压;为轴向应变。

损伤变量的表达式采用MAZARS提出的混凝土材料在受压条件下的损伤演化方程，该方程应用简便，并且符合本文以峰值点为损伤起点的假设，其表达式为

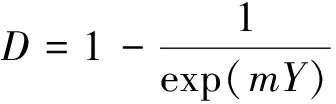
(8)

式中,为材料参数，由试验确定；为广义剪应变，其表达式为

(9)

式中，为偏应变张量；为应变张量；tr()为迹函数；为Kronecker符号张量。

常规三轴加载路径下的广义剪应变表达式为

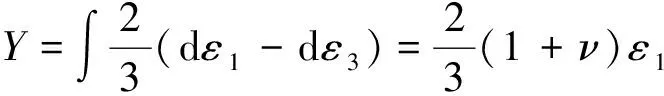
(10)

式中，为径向应变。

有学者对Mazars方程进行修正，将适用对象扩展到岩石，更好地展示岩石从低围压到高围压的脆-延性转化特征，提高对损伤阈值后岩石损伤演化过程的拟合精度，修正后的Mazars损伤演化方程为

(11)

式中，为材料参数，由试验确定。

根据损伤本构方程和损伤演化方程，对前述加卸载渗流试验得出的应力应变曲线进行拟合，确定损伤演化参数(表1)，得到的理论损伤本构曲线和损伤演化曲线如图6所示。

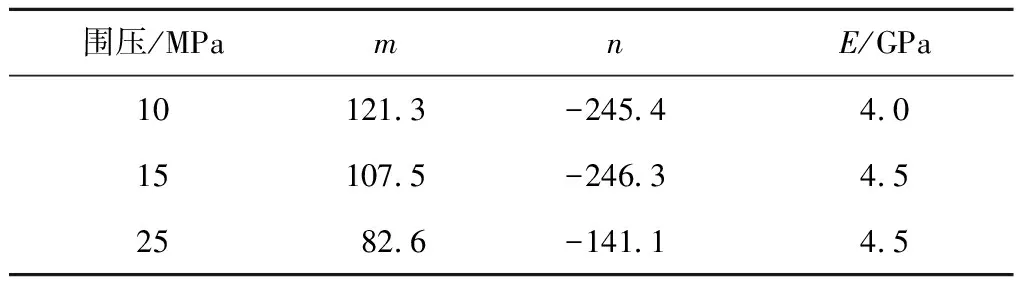
表1 损伤参数拟合结果

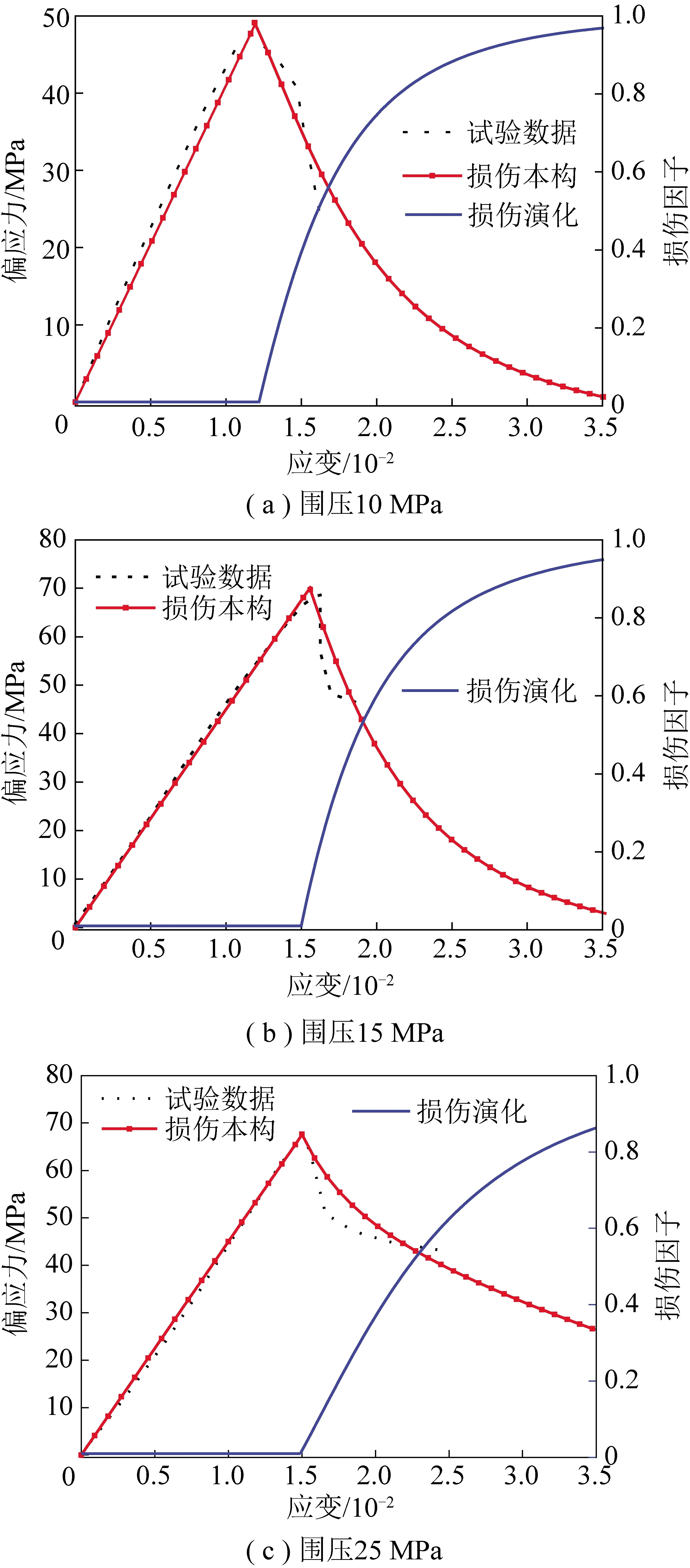
图6 理论损伤本构曲线和损伤演化曲线

由表1可以看出，围压由10 MPa增加至15 MPa，损伤应变阈值提高，围压由15 MPa增加至25 MPa，损伤应变阈值不变，但损伤演化曲线明显变缓，高围压增加了其延性。

2.2 单参数分数阶渗透率模型

分数阶渗透率模型对和这2个参数有着高度敏感性，2个参数共同决定着渗透率曲线的走势，尽管取得了不错的拟合精度，但通过试验数据拟合得出的参数值并非唯一确定，即对于峰后某个卸荷点处的渗透率比值，对应着多个和组合，而在该卸荷点处的损伤变量是唯一确定的，换句话说，和的组合关系受的控制，为此需借助损伤变量作为中间桥梁进一步探讨和的取值关系。

根据损伤演化曲线和分数阶渗透率曲线，可以确定峰后任意一点处的损伤变量值和该处的渗透率比值。在不唯一确定的情形中，其值随的变化而变化，由于阶数和损伤变量的取值范围都是[0,1]，不妨假设=，则的值可以反算得出，见表2，两参数关系的分布情况如图7所示。

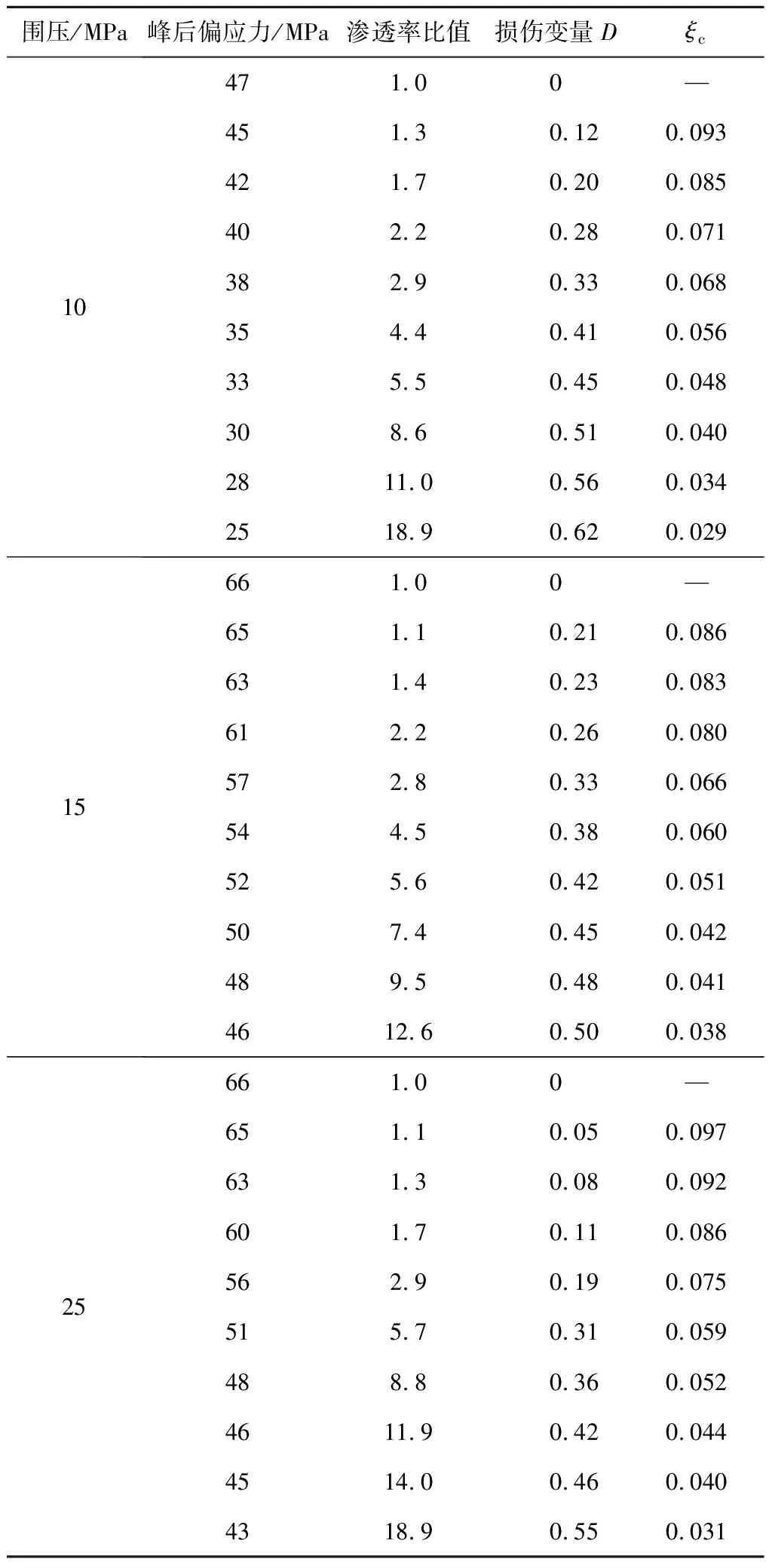
表2 模型参数计算结果

图7 γ,ξc分布关系

从图7可以看出，和这2个参数受围压变化影响较小，主要还是受损伤变量的影响，2者近似呈线性关系，由式(5)表达的分数阶渗透率模型可进一步写成

(12)

从而得到一个只含损伤变量的分数阶渗透率模型，将原模型中的静态参数修改为动态参数，更加符合卸荷煤体的实际情况。需要指出的是，对于不同性质的煤岩材料，和的关系式应根据试验重新确定。

至此，通过深入探讨分数阶渗透率模型所引入参数和的相互关系，得到了损伤变量作为中间控制条件的和的取值关系，将煤体隔理压缩系数的静态替代参数修正为符合峰后变形规律并受损伤变量所控的动态参数，弥补了现有应力-渗透率模型中所引入参数与损伤变量不关联的缺陷，使其物理意义更加清晰。

3 分数阶渗透率模型在数值模拟中的应用

3.1 煤体应力-损伤-渗流控制方程

将分数阶渗透率模型应用于充填采动煤体瓦斯渗流规律数值模拟，借助文献[13]建立的煤体应力-损伤-渗流控制方程展开研究，煤体流固耦合本构方程和流动方程分别为

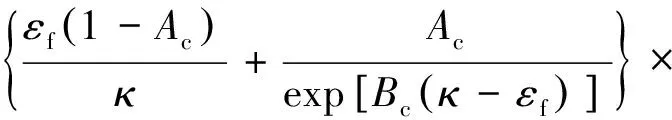
[∇+(+)∇∇·]+∇+=0

(13)

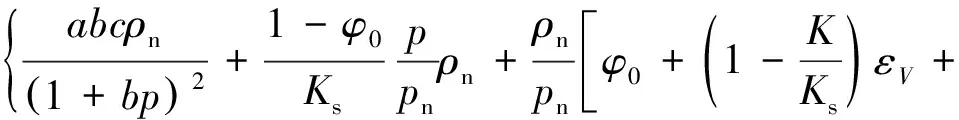
(14)

3.2 充填采动煤体瓦斯渗流规律

以山西焦煤集团东曲煤矿28802充填开采工作面为工程背景，建立充填采动瓦斯越层流动概化数值模型，采用多物理场仿真软件COMSOL Multiphysics中的平面应变模块(Solid Module)和偏微分方程模块(PDE Module)进行耦合求解，将前述煤体应力—损伤—渗流控制方程嵌入PDE模块中，分数阶渗透率模型由伽玛函数编译求解。计算域和边界条件如图8所示，充填工作面位于8号煤层，其下赋存9号煤层，煤岩体相关参数取值参考文献[13]。将充填体假设为弹性地基支承，分别模拟弹性地基系数为10，50，90 MN/m三种条件下上下2层煤体瓦斯渗流规律，重点分析充填体弹性地基系数对下邻近层煤体瓦斯流动的影响规律。

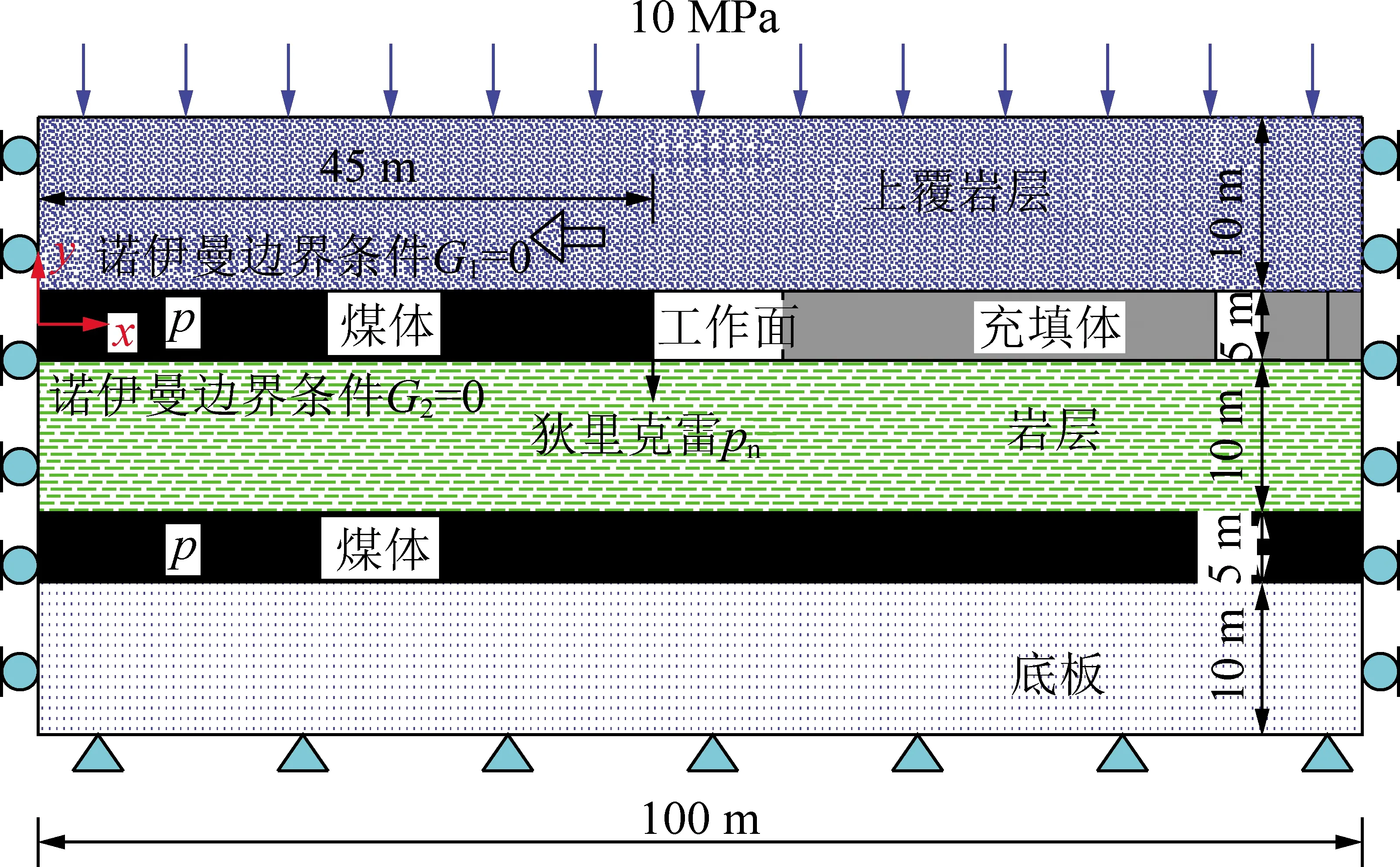
图8 充填采动瓦斯越层流动概化数值模型

采用瞬态求解器，时间步阶中的求解时间设为0～300 min，时间步长为1 min，采用全耦合算法对应力场和渗流场一次耦合求解。采用参数化扫描模拟随采充填过程，扫描步长设定为5 m。计算得出的固体力学部分(煤体损伤)和渗流力学部分(瓦斯流动)的结果分别如图9，10所示。

从图9可知，随弹性地基系数增大，充填体对顶板和底板的支承能力增强，采场整体扰动程度降低，本层煤体和下层煤体的损伤范围明显减小，充填体弹性地基系数由10 MN/m增加至90 MN/m时本层煤损伤范围由20 m减小至10 m，下层煤损伤范围由30 m减小至20 m。从图10可知，随弹性地基系数增大，瓦斯渗流速度减慢，煤体内瓦斯流出量减少。

图9 煤体损伤演化规律

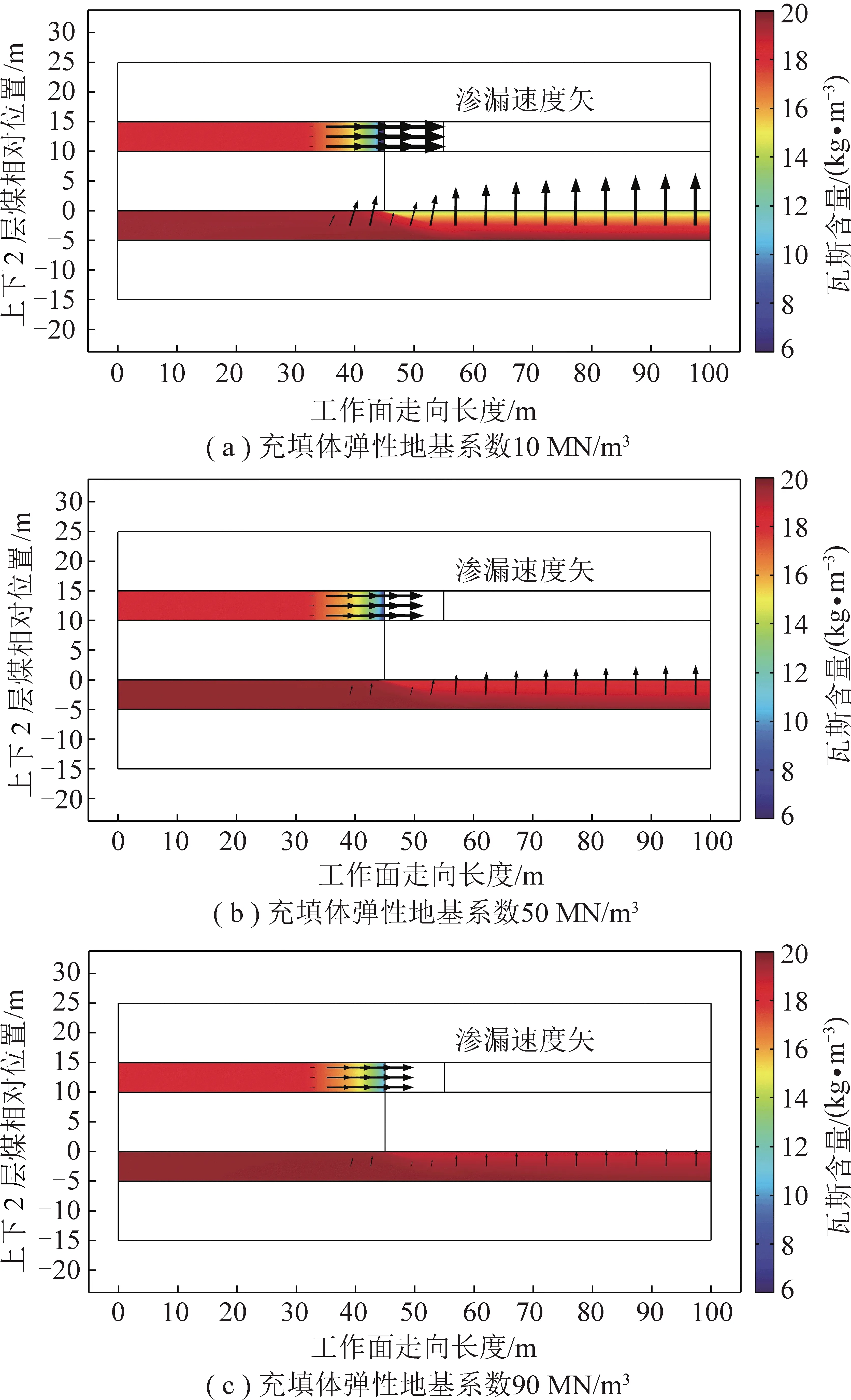
图10 瓦斯越层流动规律

根据图11显示结果，充填体弹性地基系数由10 MN/m增加至90 MN/m时，本层煤瓦斯渗流速度由0.13 m/s降低至0.045 mm/s，下层煤瓦斯渗流速度由0.018 mm/s降低至0.003 1 mm/s。根据图12显示结果，充填参数变化时，本层煤采动影响范围内的瓦斯含量的衰减总量一致而衰减速度不同，这是由采动和落煤共同影响导致的，本层煤瓦斯衰减总量均由20 kg/m减少至4 kg/m，随充填体弹性地基系数增加，瓦斯含量衰减速度减缓，临近工作面的瓦斯压力梯度大，从而增加了瓦斯突出风险；当充填体弹性地基系数为10 MN/m时，下层煤采动影响范围内的瓦斯含量衰减程度最大，由20 kg/m衰减至18.1 kg/m，当充填体弹性地基系数为90 MN/m时，下层煤采动影响范围内的瓦斯含量衰减程度最小，由20 kg/m衰减至19.2 kg/m。

图11 不同充填体弹性地基系数时上下层煤瓦斯渗流速度

图12 不同充填体弹性地基系数时上下层煤瓦斯衰减曲线

因此，提高充填体弹性地基系数，从岩层控制方面来说，有利于降低采场整体扰动程度，而从瓦斯流动方面来说，提高充填体弹性地基系数，本层煤体瓦斯流动能力变差，增加了瓦斯压力梯度，不利于瓦斯安全防治，但同时抑制住了邻近层瓦斯流动，又有利于瓦斯安全防治。总而言之，对于多煤层开采的高瓦斯矿井或瓦斯突出矿井，实施充填开采会减小采煤工作面瓦斯浓度，降低瓦斯浓度超限风险，但需要注意随之而来的本层煤瓦斯突出风险，必须加强本层煤采前预裂瓦斯抽采工作。

4 结 论

(1)分析了经典S-D模型不能适应开采卸荷煤体的原因是割理压缩系数不能随应力损伤改变，导致其表征的渗透率增大倍数有限，与采动卸荷煤体的实际不符，现有的渗透率模型通过加入具有调节倍率功能的应力敏感因子或突变系数恰是释放了这种限度而得以应用。

(2)根据改进的Mazars损伤准则，获得了煤体卸荷过程中损伤变量的演化规律，借此探讨了分数阶渗透率模型中2个参数的关系，进而得到了只含损伤变量的分数阶渗透率模型，将模型中的静态参数修正为动态参数，符合损伤扩容过程中煤体割理压缩系数不断变化的事实，弥补了现有应力-渗透率模型中所引入的静态参数与损伤变量不关联的缺陷，使其物理意义更加清晰，并且可以比较方便地应用于数值模拟和工程实践。

(3)将分数阶渗透率模型应用于充填采动煤体瓦斯渗流规律数值模拟，获得了充填采动煤体瓦斯渗流规律，提高充填体弹性地基系数，加剧了本层煤的瓦斯突出风险而减小了下层煤向本层煤涌入的采煤工作面瓦斯体积分数。因此，实施充填开采以后，存在利害两面性，特别是对于瓦斯突出矿井，充填前需加强瓦斯突出风险的评估工作。