无限稀释氯化氢水溶液中离子迁移数的测定

许新华，吴梅芬，王晓岗

同济大学化学科学与工程学院，上海 200092

1 实验原理和数据分析方法

1.1 电解质溶液浓度c → 0时迁移数与浓度的关系

根据Debye-Hückel-Onsager电导率方程[4]，对于1-1价型电解质(如HCl)，其离子摩尔电导率λ与溶液浓度c的关系可以表达为：

式中λ∞是浓度为零时的离子极限摩尔电导率。在25 °C水溶液中，若浓度c的单位是mol·L-1，摩尔电导率的单位是10-4S·m2·mol-1，则p= 30.1，q= 0.229[5]。据此，正离子的迁移数可以表达为：

若令

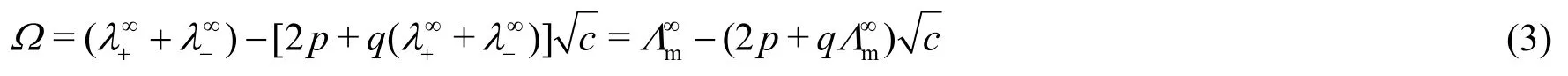
式中Λ∞m为无限稀释条件下电解质溶液的极限摩尔电导率。正离子的极限迁移数与离子极限摩尔电导率的关系为：

结合方程(3)、(4)，将方程(2)分式分子中的参数q消去，则方程(2)可以重排为：

方程(5)即为在电解质浓度趋近于0时离子迁移数与浓度的关系式。由于参数Ω也是浓度c的函数，因此t+既不与c成线性关系，也不与c1/2成线性关系。

由方程(5)可以推出无限稀释条件下，t+vs.c1/2曲线的斜率在c→ 0时应满足：

移动机器人可以自行组织运行和自主规划，其基础在于定位精度和导航准确性。通过导航定位可获得机器人所在的位置、方向，再分析实验数据，建立运动模型，从而完成路径的规划和目标跟踪。

可见，该极限斜率与t∞ +偏离0.5的差值成正比，与电解质极限摩尔电导率成反比。如果离子极限迁移数t∞ +＞ 0.5，则该极限斜率为正值，正离子迁移数随溶液浓度增大而增大；反之亦然。

1.2 实验测量数据外推离子极限迁移数的方法

方程(1)仅适用于电解质溶液浓度无限接近于零的极限浓度区[5]，如对于1-1价型电解质，c＜ 0.001 mol·L-1。界面移动法实验中电解质溶液的浓度范围一般为0.01-0.20 mol·L-1，因此上述方程对实验数据的处理是无效的。如图1所示，实验数据的测量区域与理论方程的适用区域是分离的，在两条红色虚线之间的区域就是所谓的“数据鸿沟”。若采用数据拟合方法将实验测量曲线(图1中的黑实线)外推至纵坐标轴，由于该曲线为非线性曲线，可能产生多个满足误差要求的拟合结果，从而导致数据分析结果的不确定性，即落入所谓的“局域最小化”陷阱[6]。

图1 “实实鸿沟”和拟合不确定性

为得到离子迁移数t+与溶液浓度c之间的线性关系，Longsworth[7]借鉴了Shedlovsky处理电导率与溶液浓度关系的成功案例[8,9]。首先，对实验测得的每一个浓度c对应的迁移数t+，都可以根据方程(5)计算出一个“表观极限迁移数t∞ +”，记为t0，计算公式为：

注意式中的Ω也与浓度c有关。实实证明，表观极限迁移实t0与c成线性关系，即：

将t0与c关系曲线做线性拟合，并外推到c= 0，所得截距即为正离子的极限迁移实t∞ +。

理理(8)得到的极限迁移实t∞ +是否符合1.1节中理理理理的要求呢？可以将理理(7)、(8)联立求解，得到迁移实t+与溶液浓度c的关系为：

根实理理(9)，计算t+vs.c1/2的极限斜率为：

该极限斜率与理理(6)完全相同，说明理理(8)线性拟合外推得到的极限迁移实t∞ +代入理理(9)后，其在无限稀释浓度附近理域内的变化趋势是符合Debye-Hüchel-Onsager理理模型的。

由理理(8)外推得到极限迁移实t∞ +后，就可以通过理理(9)计算出高浓度条件下离子迁移实t+vs.c1/2的拟合曲线，并考查实实实实实实与理理计算结果之间的相符理度。

2 教学实实可行性实证

上述理法能否应理于本科教学实实，是一个尚有待检实的问题。根实文献实实[10]，在实实实实浓度范围内，H+的迁移实变化范围为0.82-0.83之间。采理常规实实教学手段获得的实实实实是否能够以满意的精度符合理理(8)的线性关系，是检实实实设计是否成功的关键。此外，最终外推得到的H+极限迁移实的值与文献值之间的误差大小，也是重要的考实因素。

在现有的物理化学实实教材中，界面移动法实定离子迁移实的实实原理和理法已有详细描述，在此不再重复。经典实实采理金属镉(Cd)作为阳极，但是镉及其电解产物镉离子的毒性较大[11,12]，不理合一次实实中大实或多批次使理。吴舒婷等[13]提出可以理铜电极代替镉电极，对0.1 mol·L-1盐酸溶液中H+迁移实的实实表明，采理铜电极或镉电极所得的结果一致，并与文献值相符。本实实以铜电极为电解阳极，以铂电极为电解阴极，用0.05%甲基紫溶液为指示剂，测定浓度为0.02-0.20 mol·L-1范围内的一系列盐酸溶液的迁移数，并外推至无限稀释条件下的极限迁移数。

实验采用恒电流法，电迁移管为内径8 mm玻璃直管，总刻度容量2.0 mL，刻线分度0.1 mL，带恒温水夹套。阳极采用4 mm2铜导线，插入端剥出长度约5 mm的铜线，用细砂纸打磨去除氧化层后清洗干净备用；阴极采用铂丝电极。直流电源为LQY型直流恒流电源(南京桑力电子设备厂)，电流测量采用指针式精密直流电表(最小分度0.05 mA)。实验中需根据不同盐酸溶液的浓度调节电流大小，使得溶液界面扫过0.1 mL体积的时间不低于8 min。为保证界面清晰，指示剂的用量固定为每100 mL溶液中含指示剂5 mL。

图2中给出了根据三组学生实验测量结果计算得到的表观极限迁移数t0vs.盐酸溶液浓度c数据点及其对应的拟合直线。三组实验数据采用同一系列浓度的盐酸溶液，但是由不同学生实验小组在不同仪器上完成。三个实验获得的t0vs.c拟合直线成果如下：

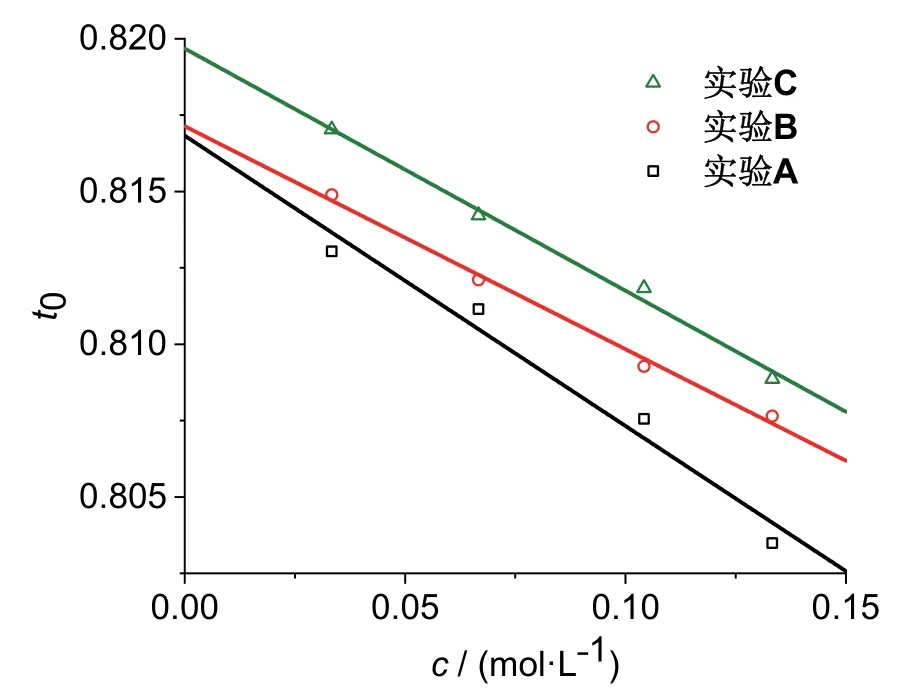
图2 t0 vs. c实验数据及其拟合直线

从实验数据可以看出，虽然三组平行实验数据不是完全一致，其中实验A的拟合直线线性也不是非常理想，但是作为一个学生实验而言，有以下几个方面的可取之处：

(1) 三组平行实验t0vs.c的拟合直线均表现出负斜率，即t0值随溶液浓度c的下降而上升，这是符合文献对盐酸溶液的测量结果的[7,10]；

(2) 三组平行实验获得的拟合直线截距，即H+的极限迁移数t∞ +分别为0.8168、0.8171和0.8197，平均值为0.8179 ± 0.0013，平行实验的数据重现性较好，标准偏差较小，相对偏差 ＜ 1.6‰。

根据文献数据[7,10,14]，盐酸溶液中H+的极限迁移数t∞ += 0.82085，我们实验测量的结果均低于文献值，相对误差为3.6‰ (其中实验A的相对误差最大，为5.0‰)，略高于平行实验数据间的相对偏差。由于平行实验测量数据均偏向文献值的低侧，因此实验值与文献值间的误差应归属于系统误差，其产生的主要原因是实验中使用铜电极代替传统的镉电极，而Cu2+不像Cd2+具有明显的颜色，因此必须在盐酸溶液中额外添加酸碱指示剂以形成清晰的界面，实验中还发现，通电一段时间后阳极附近的溶液颜色逐渐变浅直至变为无色，说明添加的指示剂发生了电氧化脱色反应，这个现象也在相关文献中被注意到[15]。脱色反应消耗了阳极氧化给出的一小部分电子，导致用于溶液中离子迁移的电量相应减小，使得实验测得的离子迁移数相应降低。由此可见，采用“铜电极+酸碱指示剂”体系代替传统的镉电极，会引入一个实验系统误差，且该误差略大于平行实验间的相对误差。甲基紫在本实验条件下的电氧化脱色反应尚未见研究报道，粗略观察发现，0.01 mol·L-1溶液的初始脱色液体体积增长量与界面移动体积之比约为1 : 6，估算消耗于电氧化脱色反应的电量约为总电量的1.5%；随着电解进行，阳极附近溶液中的指示剂基本耗尽，远端溶液中的指示剂需通过缓慢扩散才能到达阳极，脱色反应效应明显减弱，实验中观察到电解实验初始阶段测得的迁移数明显偏低，随着电解的进行，当界面移动体积大于0.5 mL后，测得的迁移数基本趋于稳定；同时，当溶液浓度增大后，由于指示剂浓度始终不变，脱色反应消耗的电量比例相应降低，使得测量误差也随之降低。因此，学生实验时盐酸浓度应控制在0.02 mol·L-1以上，以降低实验测量的误差。虽然采用镉电极会完全消除这个误差，但是考虑到有效降低学生实验产生的有毒有害废弃物的因素，且采用铜电极获得的实验结果与理论分析具有相同的、可重复的变化趋势，我们仍然建议采用“铜电极+酸碱指示剂”体系进行实验教学工作，同时建议结合综合化学实验课程或开放实验课程中的电催化氧化实验内容，引导学生对这一问题进行拓展性研究。

由上述数据分析方法得到氢离子的极限迁移数t0后，可以将其代入方程(9)中，结合方程(3)计算出迁移数t+与溶液浓度c的二分之一次方间的拟合曲线，并与实验测量数据进行对比。图3是三组平行实验所得的t+vs.c1/2数据点及其对应的理论计算曲线，可以看出在数据测量范围内，理论曲线与实验数据的吻合度还是比较好的。虽然三组平行实验数据之间存在一定误差，但是结合图2的曲线可以看出，每个实验的t0vs.c关系和t+vs.c1/2关系是相互自洽的。

图3 t+ vs. c1/2实验数据及其理论计算曲线

3 讨论和总结

实验结果表明，通过测量一系列不同浓度盐酸溶液的离子迁移数，是可以采用Longsworth外推方程获得氢离子的极限迁移数的。如果将上述内容设计为教学实验，大约需要8课时，基本满足高年级本科生的专业实验要求，与传统的只进行单一浓度溶液迁移数测定的实验设计相比，新的实验教学内容具有如下优点：

(1) 虽然增加了实验时长，但是获得的实验数据更多，对实验数据的处理和计算内容更为丰富，比如利用方程(8)进行的线性拟合与外推，以及利用方程(9)进行的非线性拟合等，这对于培养学生的数据分析能力是有益的。同时，对一系列实验数据的趋势性分析能够让学生和教师对实验结果的好坏有直观的了解，这比简单地对比文献数据更有意义。

(2) 新的实验设计有效关联了电解质导电理论，使得物理化学理论教学内容在实验课程中得到生动体现。但是可以注意到这样一个事实，即经典的Debye-Hückel-Onsager电导率方程并不能在极限迁移数测量的问题上直接运用，而必须通过巧妙的实验设计和数据分析方法，迂回达到目的。这首先说明了一个科学理论的应用实际上是有边界的，当实践过程在理论边界之外时，往往会导致结果的不确定性(见图1)；其次，因为极限条件下(本实验为无限稀释的溶液)的数据是很难测量的，新的实验设计还可以向学生展示科学知识如何来源于实验的问题。

(3) 新的实验设计还很好地诠释了化学应该如何看待和应用数学的问题。从方程(1)到方程(6)都是非常精彩的数学分析过程，但是对于解决极限迁移数的测量问题完全不起作用，解决这个问题依靠的是Longsworth提出的方程(8)，这实际上应该说是一种“化学直觉”。也就是说，当我们在应用物理学理论和数学方法把化学问题精确化的同时，必须首先依靠从实验获得的“化学直觉”，因为一切的化学知识实际上都来源于实验。

综上所述，除个别物理学常数测量内容外，在一个物理化学实验项目中仅测定单一参数的教学设计并不十分可取，但是在国内高校的物理化学实验教学中，这一类的实验设计还是比较常见的，比如经典的燃烧热测量实验等，在这方面，我们与国际先进的物理化学实验教学水平还有不少差距[16]要进一步努力。