中国棉花期货收益特征和波动性分析

黄一轩

(南京林业大学 经济管理学院, 南京 210037)

1 引言

我国已经成为世界最大棉花消费国、第二大棉花生产国，棉花在中国的农业和纺织业中都发挥着举足轻重的作用。当前，棉花交易市场主要分为现货市场和期货市场。2004年6月，我国棉花期货于郑商所正式诞生。经过多年实践和完善，棉花期货市场越来越受到公众的认可，交易的参与度也越来越高。棉花期货不仅能完善中国棉花交易体系，企业、中小投资者和机构投资者也可以运用棉花期货套期保值对冲风险，因此研究棉花期货收益特征和波动性有着非常现实的意义。

当前文献对棉花收益特征和波动的研究主要从以下几点展开。一是讨论哪些因素导致了棉花价格的波动。丁建国和穆月英(2018)[1]研究发现针对棉花价格的改革措施和市场政策的更迭引起了棉花市场价格的变动。刘光俊和胡继连(2016)[2]选取ARCH族模型探究山东省棉价波动，发现供需变动是最重要成因。二是棉花价格的波动特征的建模和拟合分析。张利召等(2021)[3]结合经济发展的不确定性综合分析了新疆棉花价格整体的波动趋势和季节周期的规律性。苏念思等(2014)[4]使用了ARCH族模型并结合HP滤波法实证分析了郑商所棉花期货价格的波动情况。三是棉花现货和期货价格的相关性分析。郭少红等(2019)[5]验证了市场情绪、棉花期货价格和棉花现货价格三者存在着非线性的关系。杨艳军和胡子晴(2019)[6]结合政策变动研究得出了棉花现货和期货之间有明显的非线性关系的结论。

从当前文献中可以看出，国内大多数研究棉花产业的文章都从棉花现货价格入手，运用滤波法等方法，并建立了ARCH族等多种模型研究棉花收益率特征、价格波动情况。相对而言，研究棉花期货的文章较少，对中国棉花期货进行系统的收益特征和波动性研究的文章更少。因此，本文旨在选取棉花指数连续合约价格为研究对象，运用GARCH和EGARCH模型，系统地分析中国棉花期货收益特征和波动性分析，对合理调控棉花价格、持续提升棉花期货价格发现功能、完善棉花期货市场提供理论依据。本文的创新之处主要有以下两点：一是运用t分布结合EGARCH等模型，从实证角度系统分析了中国棉花期货的波动特征，并深入分析原因从而提出了针对性的政策建议；二是在模型分析之外，引入了信息冲击曲线，更加形象地刻画出棉花期货市场面对利好和利空消息时的不同反应，以达到更加全面地剖析中国棉花期货市场的波动情况的目的。

2 数据选取与处理

2.1 数据选取

本文选取郑州商品交易所2011年6月10日到2021年6月10日的棉花期货指数连续合约价格为研究对象，总计 2 402 个样本数据(数据来源于布瑞克农业数据库，数据处理和作图使用R语言软件)。本文样本之所以选择棉花期货指数连续合约价格，是为了克服期货价格存在的不连续性的问题，从而更好地进行棉花期货价格走势和收益特征的刻画[7-9]。

2.2 数据处理

为了更好地对棉花期货的收益情况进行分析，对棉花期货收盘价进行一阶差分处理，以保证收益序列的平稳性。运用公式rt=(lnpt-lnpt-1)×100将棉花期货的收盘价转换为日对数收益率，其中，rt是日对数收益率，pt为当日收盘价，pt-1为上一日收盘价，在此基础上进行棉花期货的收益率特征和波动性分析。

3 棉花期货收益特征分析

3.1 棉花期货价格趋势分析

首先运用R软件绘制棉花期货的价格走势图(见图1)。从图中可以明显地看出来，从2011年达到高点后，棉花期货价格不断下跌，并在2016年触底。2011年到2016年这一期间的断崖式下跌主要是由于棉花产量供过于求以及纺织业的低迷。2016年到2020年期间，棉花期货价格先涨后跌，但是由于国家棉花目标价格补贴等政策的落实，波动幅度要小于上一个区间。从2020年初到目前，棉花期货价格呈现稳步上涨的趋势。整体来看，目前我国棉价的市场机制已经逐步形成，政府对棉价的监管和风险预警能力逐渐增强，可以预计，棉花期货价格在很长一段时间内会呈现小幅度波动的趋势[10]。

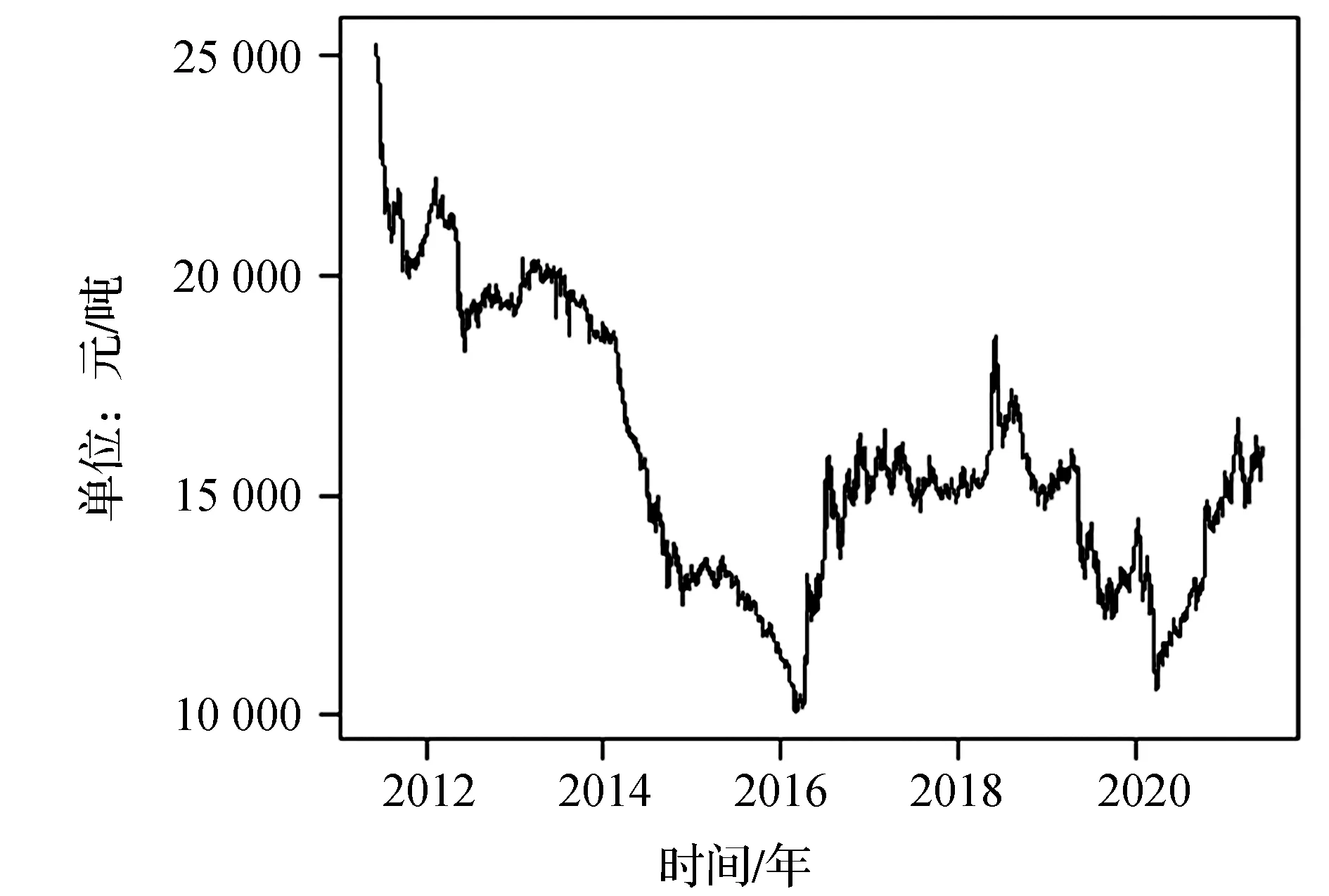
图1 棉花期货价格走势图

从表1中可以看出，价格偏度大于0，其分布呈现右偏。峰度为2.32，大于0但是小于3，说明相较于正态分布，棉花期货价格的分布较为平坦。

表1 棉花期货价格的描述性统计(元/t)

3.2 棉花期货收益率序列波动分析

根据上文一阶差分处理过的棉花期货日对数收益率数据绘制出时间序列图(见图2)。从图2中可以看出，收益率总体围绕着0上下波动，并且波动呈现“丛聚”的现象。从图上可以看出，在2017年附近的剧烈波动后，又紧跟着出现一次幅度较大但逐渐递减的波动；同样，2019年附近出现小幅度波动后，又连带产生一系列的小波动。

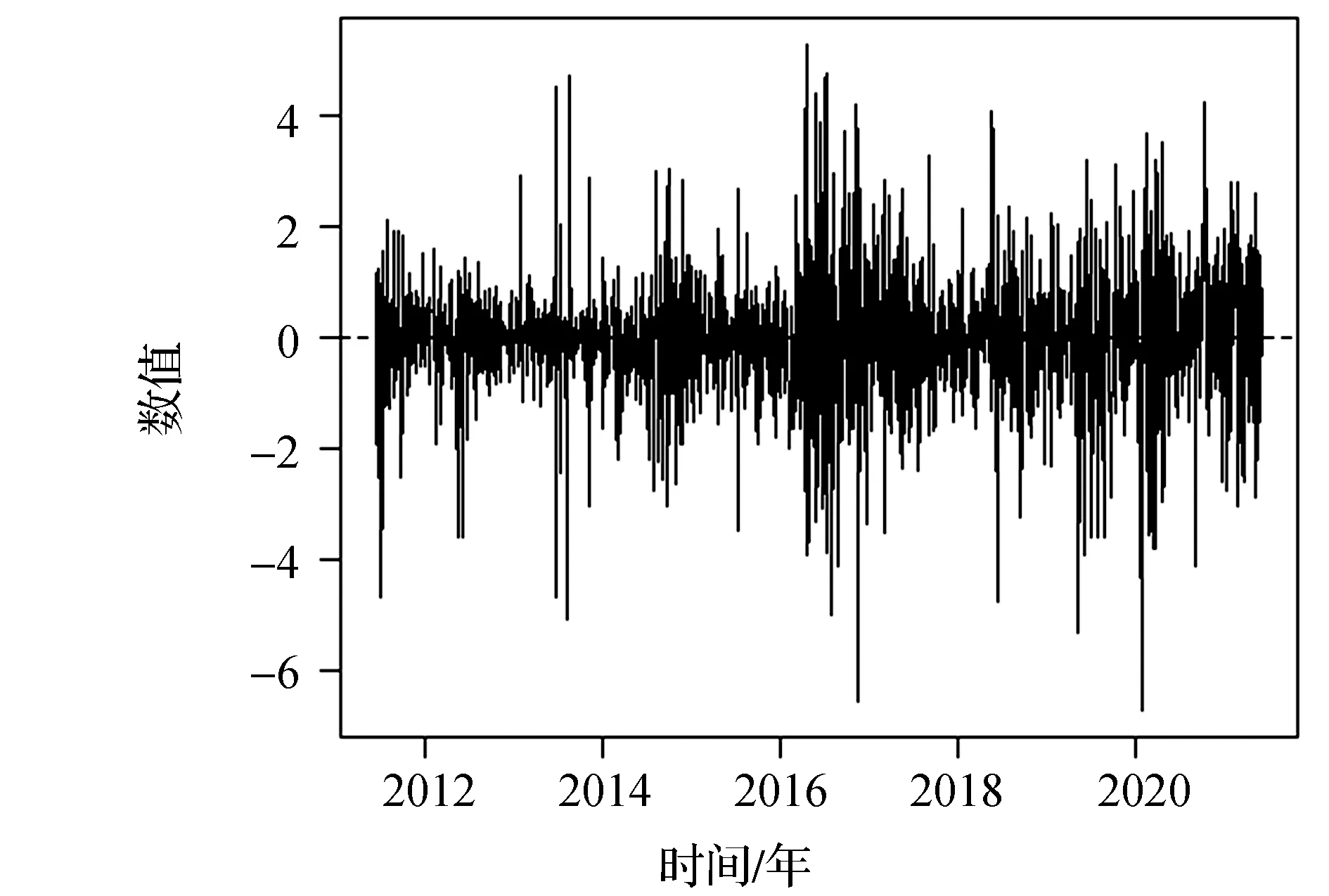
图2 棉花期货日对数收益率时序图

从棉花期货收益率的描述性统计可以发现，收益率的偏度为0.19，大于0，说明收益率分布相对于正态分布具有较长的右尾，为右偏的。收益率的峰度为4.42，大于正态分布的峰度值(见表2)。因此，可以初步判断棉花期货的收益率呈现“偏态”和“尖峰厚尾”的特征。

表2 棉花期货收益率的描述性统计(元/t)

4 模型构建和风险度量

4.1 数据检验

基于棉花期货收益率呈现的基本特征，本文进一步通过建模来刻画棉花期货的波动情况。首先进行正态性检验，运用Q-Q图可以发现该序列与正态分布的不符合程度。从图3中可以明显看出棉花期货的日收益率序列偏离了正态分布，且具有明显的尖峰肥尾特征。

图3 棉花期货日对数收益率Q-Q图

再用ADF检验来判断棉花期货收益率的平稳性，结果显示Dickey-Fuller值显示是-13.162，P值为0.01，小于0.05，说明在5%的显著性水平上呈现显著的平稳状态。接着，ARCH-LM检验可以用来判断序列的ARCH效应,结果显示p值接近于0，表明该序列存在显著的ARCH效应，可以进一步建模分析。

4.2 模型拟合

针对棉花期货收益率的特征，相较于需要更多滞后项的ARCH模型，使用GARCH模型的拟合效果会更加理想，同时学生t分布比正态分布更能反映收益率的尖峰肥尾特征，因此，本文结合学生t分布和GARCH模型建立GARCH(1,1)-t模型，其表达式为：

式中，ω1是均值方程的常数项系数，εt是随机误差项，α1和β1分别是ARCH项和GARCH项的系数，λ1是偏度系数。以下是参数估计结果：

表3 GARCH(1, 1)-t参数估计结果

由表3可知，ω1、α1、β1、λ1的P值均小于0.01，也就是说在99%的置信水平下是显著的，验证了棉花期货收益率的丛聚效应。并且α1与β1两者相加是 0.995 5，小于但很接近1，说明在棉花期货市场中，曾经的波动对未来价格的冲击是相对持久的，并且随着时间的推移递减。偏度系数λ1=3.6344>1，表明棉花期货收益率的分布为右偏的。

进一步运用EGARCH模型来刻画非对称性，依然使用能反映尖峰厚尾特征的学生t分布来刻画收益率的分布情况，构建EGARCH(1,1)-t模型，在该模型中，μ表示均值方程的常数项，ω2表示方差方程的常数项，α2和β2分别是ARCH项和GARCH项的系数，λ2表示偏度系数，参数γ为非对称性系数，只要γ≠0，那么就可以说明信息冲击的作用是非对称性的，以此来分析棉花期货收益率是否具有“杠杆效应”。以下是参数估结果：

从表4中可以看出，几个重要参数α2、β2、γ、λ2的P值都小于0.05，说明在95%的置信水平下是显著的。其中，γ=-0.2298≠0，说明棉花期货价格的波动具有非对称性，并且γ<0，表明棉花期货市场中利空消息带来的冲击要大于等量的利好消息，棉花期货价格波动具有明显的杠杆效应。

表4 EGARCH(1, 1)-t参数估计结果

4.3 信息冲击曲线

为了更加形象地刻画出利好消息和利空消息对我国棉花期货市场的不同影响，本文进一步作出了棉花期货市场的信息冲击曲线。

从图4中可以看出，棉花期货市场在面对利空和利好消息时，其信息冲击曲线均呈现陡峭走势，这就说明了棉花期货市场的稳定性较弱，对消息过于敏感，抗风险能力弱。因此，政府需要进一步完善棉花期货市场的信息披露制度，更好地发挥棉花期货市场的价格发现和规避风险功能。

图4 棉花期货收益率信息冲击曲线

5 结论

本文以郑商所棉花期货市场收益率为研究对象，经过数据建模和分析后，得到了以下研究结论：①棉花期货收益率序列呈现尖峰厚尾、偏态、波动集聚性等特征。②在棉花期货市场中，过去的波动对未来价格的影响相对持久，并且随着时间的推移递减。③棉花期货市场杠杆效应明显，利空消息会比利好消息对棉花期货市场产生更加强烈的冲击。④棉花期货市场的稳定性较弱，对消息过于敏感，抗风险能力弱。