利用一“数”一“形”巧解天体运动问题

甘肃 赵强强 石小娟

(作者单位：甘肃省甘谷县第四中学)

天体运动问题是高考必考内容之一，近几年随着我国航空航天事业的发展，考查天体运动的试题情境越来越新，学生也感觉这类试题越来越难。天体运动问题就是一个动力学问题，涉及的主要知识有匀速圆周运动、万有引力定律、功能关系等。现有的大多数研究主要是对问题进行分类，而后针对每一类问题提出相应的解决办法，这使学生认为这类问题比较复杂，理解记忆也比较困难。事实上，天体运动问题本身涉及的物理量确实比较多，其中有些物理量易混淆，又由于情境的不断变化，让问题的解决变得更加困难。为此，本文总结了一个普遍通用的数学公式和一个普遍适用的图形，利用这一“数”与一“形”相结合来帮助学生快速准确的解决有关天体运动的问题，并以高考真题为例，演绎解题过程。

一、归纳总结一“数”一“形”

在高中教学中，处理天体运动问题时有两个近似，一是将行星绕中心天体的椭圆轨道运动近似为做匀速圆周运动；二是物体在天体表面附近时，近似认为物体的重力等于万有引力。接下来，我们将在这两个前提下分析处理天体运动问题。首先，需建立一个图形，其用于展示一个天体运动系统及其相关的各个物理量，如图1所示。在图1中M、R、g分别表示中心天体的质量、半径和天体表面的重力加速度；m、v、ω、T、an、h分别表示行星的质量、线速度、角速度、周期、向心加速度和距中心天体表面的高度，r为行星绕中心天体运动的轨道半径，易知r=R+h。

图1

G表示引力常量；根据万有引力定律和第一个近似可知，行星绕中心天体做匀速圆周运动适用的关系式为

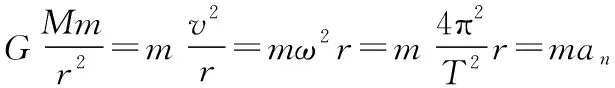
再根据万有引力定律和第二个近似可知，物体在天体表面附近时适用的关系式为

综合①②两式可得到一个普遍适用的关系式

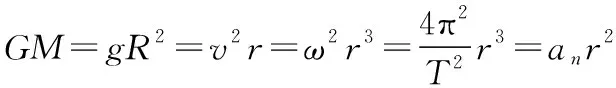
笔者将③称之为“万能公式”，为了方便后面描述，依次把每一项称作有M项、g项、v项、ω项、T项和an项。结合图1和“万能公式”，我们可以快速、准确的解决有关天体运动的绝大多数问题。

二、演绎利用一“数”一“形”相结合的解题过程

1.求解行星运动参量

【例1】(2018·全国卷Ⅲ·15)为了探测引力波，“天琴计划”预计发射两颗地球卫星P，其轨道半径约为地球半径的16倍，另一地球卫星Q的轨道半径约为地球半径的 4倍。P与Q的周期之比为

( )

A.2∶1 B.4∶1 C.8∶1 D.16∶1

【答案】C

【例2】(2020·浙江省7月选考·7)火星探测任务“天问一号”的标识如图2所示。若火星和地球绕太阳的运动均可视为匀速圆周运动，火星公转轨道半径与地球公转轨道半径之比为3∶2，则火星与地球绕太阳运动的

( )

图2

A.轨道周长之比为2∶3

D.向心加速度大小之比为9∶4

【答案】C

2.计算中心天体质量

【例3】(2020·全国卷Ⅱ·15)若一均匀球形星体的密度为ρ，引力常量为G，则在该星体表面附近沿圆轨道绕其运动的卫星的周期是

( )

【答案】A

3.比较两个行星的运动参量

【例4】(2020·浙江省1月选考·9)如图3所示，卫星a、b、c沿圆形轨道绕地球运行。a是极地轨道卫星，在地球两极上空约1 000 km处运行；b是低轨道卫星，距地球表面高度与a相等；c是地球同步卫星，则

( )

图3

A.a、b的周期比c大

B.a、b的向心力一定相等

C.a、b的速度大小相等

D.a、b的向心加速度比c小

【答案】C

【总结】不管是求解(比较)行星运动参量问题，还是计算中心天体质量和密度的问题，只需要将题目描述过程和图1对应，再找到公式③中与已知量和要求量对应的项组成的等式，就可以进行相应的分析和计算。值得注意的是，在解决这些问题时，首先要确定天体系统，找准中心天体，尤其在计算质量和密度时只能计算的是中心天体的质量和密度。其次，要注意区分天体半径R和轨道半径r，二者之间的关系是r=R+h，但当题目中出现天体表面或者天体表面附近时，通常认为r=R。

4.能量问题

【例5】(2017·全国卷Ⅱ·6)(多选)如图4，海王星绕太阳沿椭圆轨道运动，P为近日点，Q为远日点，M、N为轨道短轴的两个端点，运行的周期为T0，若只考虑海王星和太阳之间的相互作用，则海王星在从P经M，Q到N的运动过程中

( )

图4

B.从Q到N阶段，机械能逐渐变大

C.从P到Q阶段，速率逐渐变小

D.从M到N阶段，万有引力对它先做负功后做正功

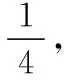
【答案】CD

5.卫星的变轨问题及卫星的发射与回收问题

【例6】(2019·陕西省山阳中学模拟考试·4)2018年12月12日，我国发射的“嫦娥四号”探测器进入环月轨道1，12月30日实施变轨进入环月轨道2。其飞行轨道如图5所示，p点为两轨道的交点。如果嫦娥四号探测器在环月轨道1和环月轨道2上运动时，只受到月球的万有引力作用，环月轨道1为圆形轨道，环月轨道2为椭圆轨道。则以下说法正确的是

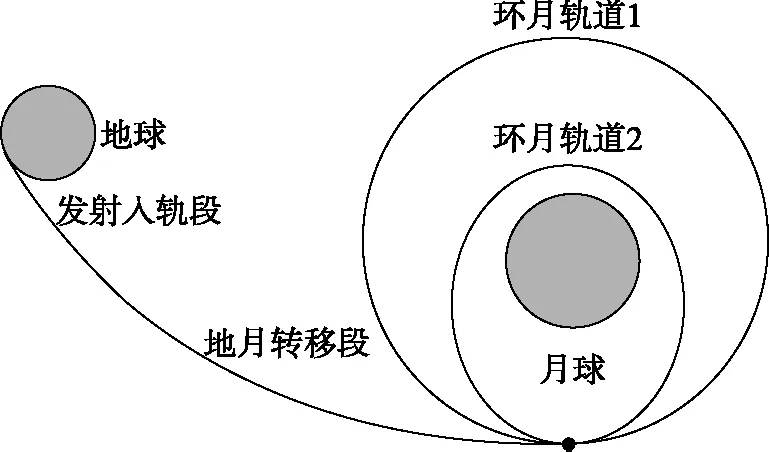
图5

( )

A.若已知嫦娥四号探测器环月轨道1的半径、运动周期和引力常量，则可以计算出月球的密度

B.若已知嫦娥四号探测器环月轨道2的近月点到月球球心的距离、运动周期和引力常量，则可以计算出月球的密度

C.嫦娥四号探测器在环月轨道2上经过p点的速度小于在环月轨道1上经过P点的速度

D.嫦娥四号探测器在环月轨道2时，从近月点运动向远月点P的过程中，加速度变大

【解析】对于A选项，选取公式③中有M项和T项组成等式可求出M，但是不知道月球半径，无法计算其密度；对于B选项，由于是椭圆轨道，所以公式并不适用，也无法计算月球密度；对于C选项，由于探测器做近心运动，所以其速度要在p点减小；对于D选项，探测器在从近月点向远月点P运动的过程中r逐渐增大，选取公式③中有M项和an项，可得GM=anr2，易知当r逐渐增大时，an逐渐变小。综上可知，C正确。

【答案】C

【例7】(2021·天津等级性考试·5)2021年5月15日，天问一号探测器着陆火星取得成功，迈出了我国星际探测征程的重要一步，在火星上首次留下国人的印迹。天问一号探测器成功发射后，顺利被火星捕获，成为我国第一颗人造火星卫星。经过轨道调整，探测器先沿椭圆轨道Ⅰ运行，之后进入称为火星停泊轨道的椭圆轨道Ⅱ运行，如图6所示，两轨道相切于近火点P，则天问一号探测器

( )

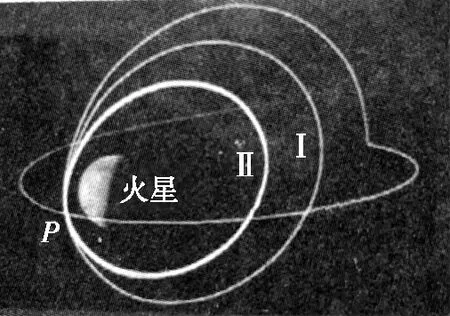
图6

A.在轨道Ⅱ上处于受力平衡状态

B.在轨道Ⅰ运行周期比在Ⅱ时短

C.从轨道Ⅰ进入Ⅱ在P处要加速

D.沿轨道Ⅰ向P飞近时速度增大

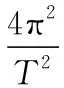
【答案】D

【例8】(多选)如图7为发射某卫星的示意图，P、Q分别为该卫星椭圆轨道Ⅰ上的近地点和远地点，轨道Ⅰ、Ⅱ相切于Q点，则

( )

图7

A.卫星在轨道Ⅱ上的运行周期大于在轨道Ⅰ上的运行周期

B.卫星在轨道Ⅱ上的线速度大于7.9 km/s

C.在轨道Ⅰ上，卫星在P点的加速度大于在Q点的加速度

D.卫星在轨道Ⅰ上具有的机械能等于在轨道Ⅱ上具有的机械能

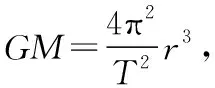
【答案】AC

【总结】卫星的变轨问题及卫星的发射与回收问题，其实质是卫星轨道半径变大或变小的问题。公式③仍然适用，利用中心天体质量不变可确定公式③中每一项都不变，再利用r的变化可确定其他几个物理量的变化。但要注意两点，一是卫星在变轨瞬间要做离心或近心运动，就需要在短时间内进行加速或者减速，因此在没有进行加速或减速时，由于只有万有引力做功，故卫星的机械能守恒；在发射卫星或者加速后，卫星的机械能将增加；在回收卫星或者减速后，卫星的机械能将减小。二是涉及速度时，要区分是发射速度还是运行速度，是瞬时速度还是稳定运行时的速度。

三、总结与展望

在高考中有关天体运动的问题多数是以选择题的形式进行考查，只需要得到最后的结果，而不用展示分析过程，所以在考试过程中，只需要将题目中的物理情境对应到笔者总结的“形”中，再将题目给出的已知量和需要求解的量对应到“数”中，找到对应的项建立等式，就可以快速准确地解决问题。笔者对一“数”一“形”相结合的方法进行了大量的解题实践验证，并指导学生运用此方法来解决相关问题，不断收集学生运用此方法时所遇到的各种问题，并对此方法进行修正和完善，最终得到现有的结论。实践证明，此方法能够很好地解决天体运动问题，更为重要的是有利于培养学生利用数形结合的思想方法分析处理物理问题的能力，提高学生的物理核心素养。