运用“拉前腿”法巧解三力动态平衡问题
2022-07-29云南李鑫磊
云南 李鑫磊
(作者单位:瑞丽市畹町经济开发区中学)
三力动态平衡是指物体在三个力(受到多个力时可等效为三个力)的作用下缓慢运动并处于一系列的平衡状态。力学动态平衡是高考热点问题,同时又是教学难点,此类问题涉及的题型较多,且同一个题型解法也不唯一。针对这种情况,笔者凭借多年的教学经验对此类问题的常见题型加以分析,结合力的矢量三角形提出“拉前腿”法(箭头端,笔者称之为“前腿”)。即根据物体的受力情况,先画出恒力(一般为重力)的有向线段,第二个力以恒力的前端(箭头端)开始画有向线段,第三个力以第二个力前端(箭头端)开始画有向线段,从而构成一个首尾相连的闭合三角形,再根据闭合矢量三角形有向线段的长度即可判断力的大小变化情况。“拉前腿”法可使学生更容易对物体进行正确的受力分析,更加深入地理解矢量三角形法则。根据动态平衡问题中物体受力特点,结合“拉前腿”法,笔者将力学中三力动态平衡问题归纳为两类:“一恒一定”和“一恒二变”。“拉前腿”法的具体思路和应用例析如下。
一、“拉前腿”法之“一恒一定”
“一恒”:物体所受三个力中有一个力是恒力(即大小和方向都不变的力,一般为重力);“一定”:其余两个力中有一个力定向(方向不变)、定大(大小不变)或两个力定角(两个力间夹角不变)。
1.一恒一定向
【例1】(2019·全国卷Ⅰ·19)(多选)如图1,一粗糙斜面固定在地面上,斜面顶端装有一光滑定滑轮。一细绳跨过滑轮,其一端悬挂物块N,另一端与斜面上的物块M相连,系统处于静止状态。现用水平向左的拉力缓慢拉动N,直至悬挂N的细绳与竖直方向成45°。已知M始终保持静止,则在此过程中
( )
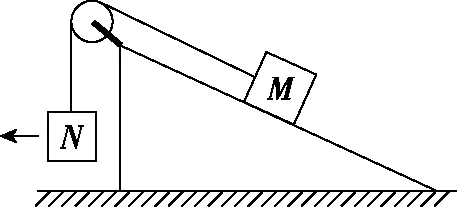
图1
A.水平拉力的大小可能保持不变
B.M所受细绳的拉力大小一定一直增加
C.M所受斜面的摩擦力大小一定一直增加
D.M所受斜面的摩擦力大小可能先减小后增加
【解析】以物块N为研究对象,先画出恒力(重力mg,此时重力的大小和方向要保持不变),再从重力箭头前端开始画方向不变的力(水平拉力F),再从水平拉力F的箭头前端开始画绳子拉力T,构成矢量三角形如图2所示,物块在水平向左的拉力F作用下,缓慢向左移动直至细绳与竖直方向的夹角为45°,从力的矢量三角形可知,水平拉力F逐渐增大,绳子的拉力T也逐渐增大。以物块M为研究对象,根据“拉前腿”法,可得矢量三角形如图3所示,由于重力G和支持力FN均为恒力,则平行于斜面的合力F斜=T±f-mgsinθ(其中f为物块M与斜面间的摩擦力)也为恒力,若初始时M受到的摩擦力f方向沿斜面向下,随着绳子拉力T的增加,则摩擦力f也逐渐增大;若初始时M受到的摩擦力f方向沿斜面向上,随着绳子拉力T的增加,则摩擦力f可能先减小后增加,故选项BD正确。
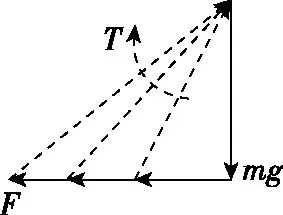
图2

图3
【答案】BD
【点评】“一恒一定向”问题,学生根据“拉前腿”法得出力的矢量三角形,再由矢量三角形中“旋转边”的变化情况,很容易判断出各个力的变化情况(如:①“竖小平大”,即旋转边越竖直,两个变力就会越小,旋转边越水平,两个变力就会越大;②“垂直极小”,即旋转边与定向边竖直时,旋转边的力达到最小值)。当物体受到三个以上的力的作用时,可以将其中的几个力先合成,再构成矢量三角形,然后根据“拉前腿”法判断各个力的变化情况。
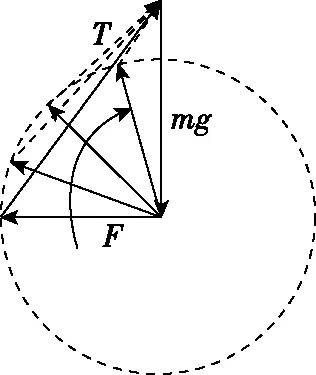
2.一恒一定大
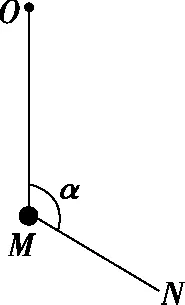
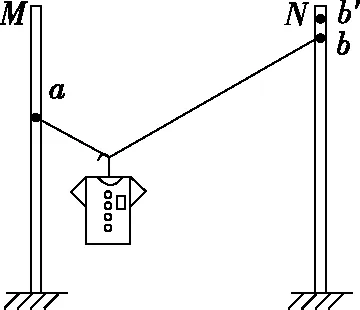
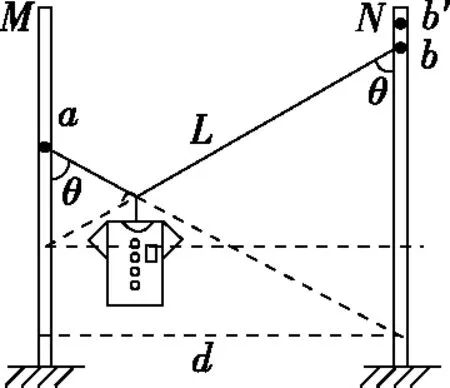
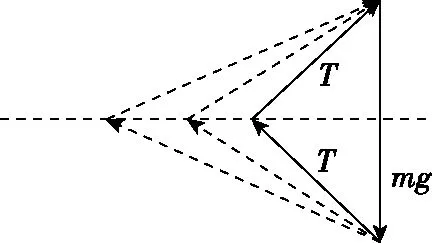
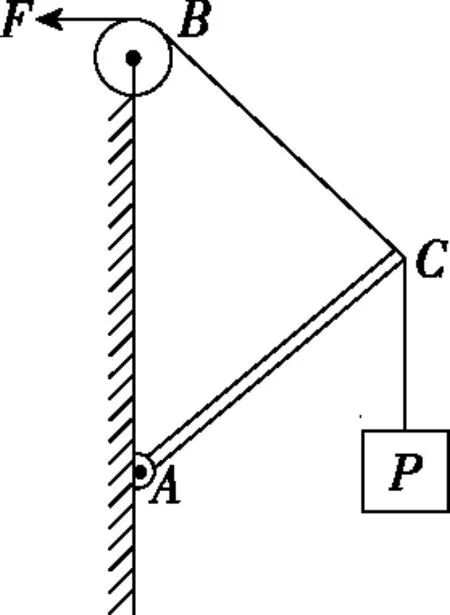
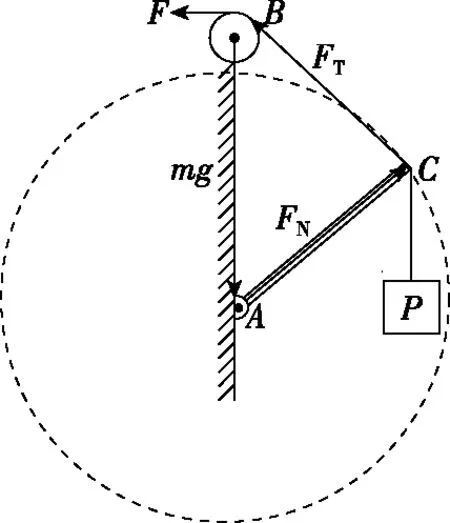
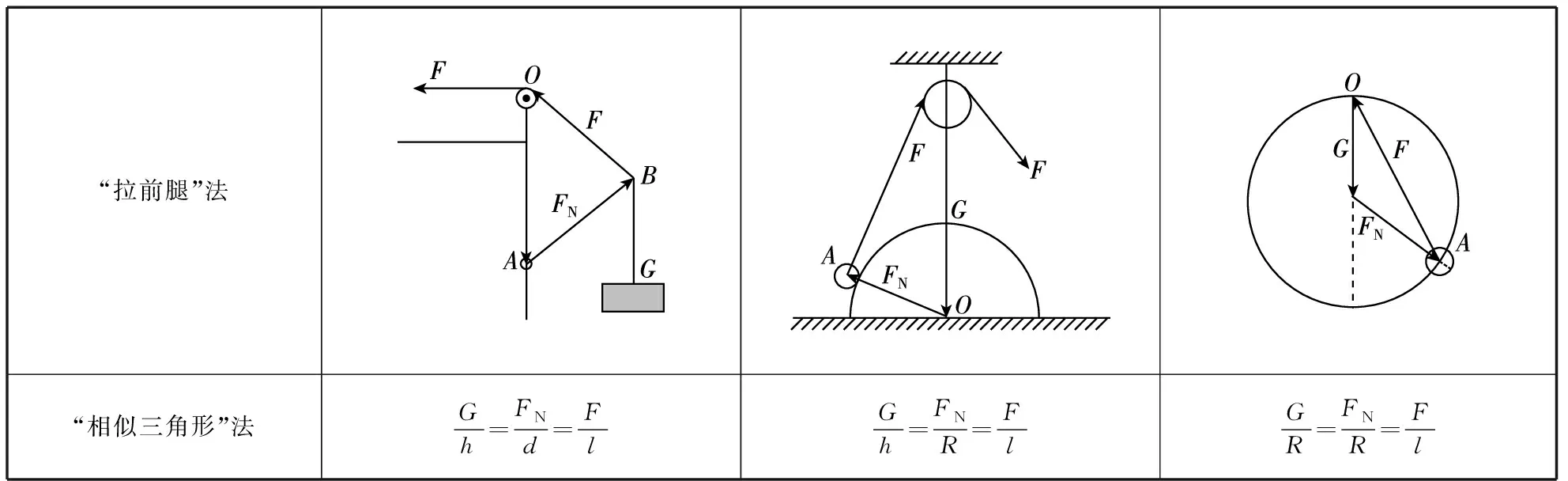
【例2】如图4所示,质量为m的小球A用轻绳悬挂于O点,用力F(F ( ) 图4 A.轻绳OA中的拉力T渐增大 B.轻绳OA中的拉力T逐渐减小 C.轻绳OA中的拉力T先增大后减小 D.轻绳OA中的拉力T先较小后增大 【解析】对小球A受力分析,先画出重力mg的有向线段,从重力有向线段的箭头端开始画出拉力F的有向线段,再画出绳子OA所受拉力T的有向线段,构成起始位置处的矢量三角形。拉力F在旋转过程中大小保持不变,因此以恒力(重力)的箭头端作为圆心,以拉力F的大小作为半径,画出如图5的辅助圆。从辅助圆上很容易看出,以F为半径顺时针旋转所构成的一系列矢量三角形中绳子的拉力T逐渐减小,故选项B正确。从图4中还可以看出,OA绳子所受的拉力与竖直方向的夹角先增大后减小,当拉力F与拉力T垂直时,绳子OA有最大偏角。 图5 【答案】B 【点评】“一恒一定大”问题,用“拉前腿”法构成初始状态的矢量三角形。以恒力(一般为重力)的箭头端为圆心,用大小不变的力作为半径,旋转得出辅助圆上一系列的矢量三角形,从矢量三角形中可以直观地判断出另一个力的变化情况,此类问题另一个变力大小的变化情况为渐变(逐渐增大或者逐渐减小),且当大小不变的力与变力垂直时,变力与竖直方向偏向角最大。 3.一恒一定角 ( ) 图6 A.MN上的张力逐渐增大 B.MN上的张力先增大后减小 C.OM上的张力逐渐增大 D.OM上的张力先增大后减小 【解析】对M端进行受力分析,先画出重力mg的有向线段,以重力有向线段的箭头端为起始画出MN的拉力TMN,以TMN的箭头端为起始画出OM的拉力TOM,构成在起始位置的闭合矢量三角形。由于TMN和TOM间的夹角保持不变,且绳子OM的长度不变,把重物向右上方缓慢拉起过程中,重物M的轨迹为圆弧,且在矢量三角形中重力为恒力,根据几何中“弦长一定时,对应的圆心角一定”很自然得到,以矢量三角形中重力矢量边为定弦作出的辅助圆,如图7所示。由图7中的动态矢量三角形可知,在OM由竖直被拉到水平的过程中,TMN逐渐增大,TOM先增大后减小。 图7 【答案】AD 【点评】虽然“一恒一定角”问题可以用拉密定理、正(余)弦定理或特殊值法解决,但是笔者认为用“拉前腿”法构成初始矢量三角形结合辅助圆更加直观、简单。关于“一恒一定角”问题,我们也可以总结出力的变化情况,即“定角最平”(在两个力夹角保持不变的三力动态平衡问题中,其中一个力的大小达到最大时,另一个力的方向一定处于水平),若在很熟悉此类问题的情况下,根据“定角最平”就可以快速解决问题。 “一恒二变”即物体所受的三个力中有一个力是恒力(即大小和方向都不变的力,一般为重力),另外两个力是变力(大小变化、方向变化、大小和方向都变化)。笔者在此又将此类问题归为两类:对称性变化型和非对称性变化型。对称性变化型是指两个变力在某种条件约束下成对称性变化(如活结类问题);非对称性变化型是指两个变力之相互制约但没有对称变化。 1.一恒二变——对称性变化型 【例4】(2017·天津卷·8)(多选)如图8所示,轻质不可伸长的晾衣绳两端分别固定在竖直杆M、N上的a、b两点,悬挂衣服的衣架挂钩是光滑的,挂于绳上处于静止状态。如果只人为改变一个条件,当衣架静止时,下列说法正确的是 ( ) 图8 A.绳的右端上移到b′,绳子拉力不变 B.将杆N向右移一些,绳子拉力变大 C.绳的两端高度差越小,绳子拉力越小 D.若换挂质量更大的衣服,则衣架悬挂点右移 图9 图10 图11 【答案】AB 【点评】晾衣架模型是“一恒二变”动态平衡类问题中典型的一类问题,在绳长不变的约束条件下,光滑挂钩(“活结”)结构,体现了绳子张力对称相等的特点。该类问题的关键是找准绳子、竖直杆间的夹角θ与绳子长度L、两晾衣杆间水平距离d之间的关系。找准几何对称关系就容易得出力学对称关系,根据“拉前腿”所得的矢量三角形,就可以直观、简单地看出各个力的变化情况。 2.一恒二变——非对称性变化型 【例5】如图12所示是一个简易起吊设施的示意图,AC是质量不计的撑杆,A端与竖直墙用铰链连接,一滑轮固定在A点正上方,C端吊一重物。现施加一拉力F缓慢将重物P向上拉,在AC杆达到竖直前 ( ) 图12 A.BC绳中的拉力FT越来越大 B.BC绳中的拉力FT越来越小 C.AC杆中的支撑力FN越来越大 D.AC杆中的支撑力FN越来越小 【解析】对C点进行受力分析,根据“拉前腿”法可得初始状态的矢量三角形,如图13所示;对起吊装置的几何三角形进行分析可知,边AB和边AC的长度不变,因此可将“拉前腿”法所得的初始矢量三角形平移到几何装置,可得到动态平衡轨迹的圆弧,由图14可直观地看出FT越来越小,FN大小不变。因此选项B正确。 图13 图14 【答案】B 【点评】“一恒二变”中非对称性变化问题最常见的解法是用“相似三角形”法(用力的矢量三角形和几何三角形相似),然而若在实际解决问题中找不到相似三角形,难度就会增加,因此笔者认为根据“拉前腿”法得出初始状态的矢量三角形,并结合几何三角形分析,将会大大降低解题难度。常见模型对比如下表所示。 “拉前腿”法“相似三角形”法Gh=FNd=FlGh=FNR=FlGR=FNR=Fl 经过分析可知,当动点轨迹是圆弧时,若能找到几何三角形中两条不变的边,则将“拉前腿”法变形为“一恒一定”模型将会快速解决问题。 三力动态平衡问题对学生而言,难度较大,但有很强的规律性,本文中笔者用“拉前腿”法将三力动态平衡问题归纳为两类,增强了动态平衡问题的内部联系,有效降低了学生解决此类问题的难度。在平时的教学中,教师可将不同的问题进行梳理和归纳并结合生产、生活实际,培养学生思维能力和解决实际问题能力,有效提高教学及备考效率。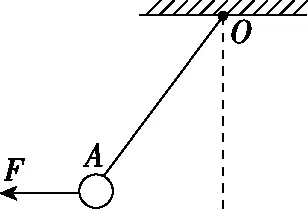
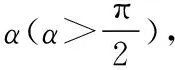
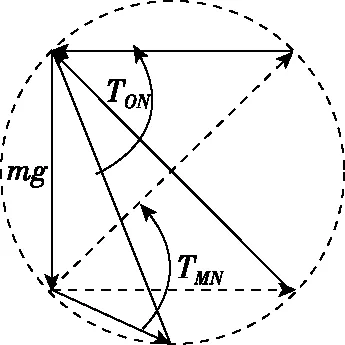
二、“拉前腿”法之“一恒二变”



三、结束语
