双势阱中利用量子非破坏性测量产生自旋压缩玻色-爱因斯坦凝聚态

季杨旭, ILO-OKEKE Ebubechukwu O., BYRNES Tim,

（1. 华东师范大学 精密光谱科学与技术国家重点实验室, 上海 200241;2. 上海纽约大学 物理系 , 上海 200122）

0 引 言

量子纠缠[1-2]是量子力学中态叠加原理作用于多粒子体系所得到的一种微观系统的量子特性. 随着这些年量子信息技术的迅速发展, 量子纠缠作为其中的核心内容得到了应有重视, 目前被广泛地应用于量子信息和量子计算等重要领域. 而量子系统的压缩态是一种具备多种应用前景的资源, 其具有纠缠特性, 可以在各种量子信息应用领域[1]、量子计量[3-4]、精密测量[5]和量子网络[6-7]中发挥很好的作用. 压缩态[8-9]的相位灵敏度超过了由单个不相关量子粒子[10]的量子噪声所导致的标准量子极限[8]. 因此, 在许多物理学领域, 如图像重建、磁测和电场传感、光学干涉和引力波检测等领域, 使用纠缠和压缩进行增强测量和检测变得越来越常见.

在不同系统中实现压缩态通常依赖于由量子粒子之间的非线性相互作用产生的量子关联或纠缠.例如, 常见的是使用Kerr 效应[11-12]产生光学压缩态[13-15], 并将其广泛地应用于各种技术中. 而在玻色-爱因斯坦凝聚态(BEC)[8,16]和捕获离子[17]等原子系统中, 常用两体自旋相互作用法产生纠缠和压缩[8,18-21]. 此外量子非破坏性测量(QND)[22-23]等技术也被用于实现原子系统中的压缩[23], 该方法测量了光脉冲通过原子样品后获得的相移. 该方法的优势在于原子共振跃迁时光探针有一个大的频率失谐,会产生非常低的光子散射率使对测量的破坏性达到最小. 该测量技术的另一个优点在于, 原子布居数的信息包含在光的相位中, 便于收集和读取. 以上这些特性被用于原子系统的量子非破坏性测量, 以在超精细原子水平之间产生纠缠[24-25], 并观察了放置在低于标准量子极限[24]的射频场中的原子的自旋旋转. 目前已经实现将原子系综上的压缩态推广到多个原子系综上[26], 这种压缩态是原子系综的量子计算应用和量子信息应用的基础[27].

本文在马赫-曾德干涉仪[28]中使用平衡检测法来产生BEC 的压缩态, 研究和表征了如何在双势阱中产生压缩自旋态, 并进行了非破坏性测量. 在无隧穿条件下是, 分析此时BEC 的概率分布表达式,以此得出BEC 的自旋相干态在光子探测后能够被压缩的结论.

1 物理模型

本文的模型系统是一个可以由磁性或光学场产生的限制在双势阱中的多体原子BEC, 如图1 所示. 由图1 可以看到, 该双势阱结构中存在BEC, 原子能够在势阱间隧穿. 图1 中, 黑色实线是双势阱;青色实线代表的对称波函数为基态 |g〉的波函数, 其能量为 ℏωg; 而红色实线代表的式反对称函数为激发态 |e〉的波函数, 能量为 ℏωe. 在双势阱的两能级近似中, 本征态是对称的和反对称的波函数, 借此形成赝自旋算符. 为了产生压缩态, 本文利用原子共振跃迁的失谐光对原子进行干涉测量. 由图1 可知,在上述规定的条件下,光子的测量引起了自旋量子态的改变, 但却保证了其平均自旋方向不变.

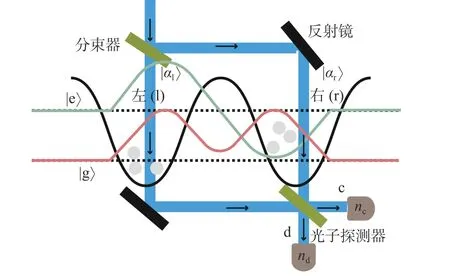
图1 允许原子隧穿的双势阱BEC 模型Fig. 1 A double-well BEC trap containing atoms that are allowed to tunnel between the wells

原子-光系统经量子非破坏性测量所得的哈密顿量为

在初始时刻, 原子随机分布在2 个势阱中, 原子的状态为对称态和反对称态的线性叠加, 即

利用湮灭算符be,bg构造施温格 (Schwinger) 玻色算符, 并将上述湮灭算符be,bg用bl,br替换, 由此不难得到一组类似于施温格玻色算符的有效算符, 即

假设双势阱中BEC 中的原子总数为N,N是个常量, 可得

这里原子数算符是福克 (Fock) 态的本征值, 可以记作

由公式 (5) 可以得出, 算符Jx的物理意义是计算左右两势阱中的相对原子数量; 算符Jz的物理意义是双势阱中激发态和基态的相对原子数量差; 算符Jy的物理意义则是表示两势阱中BEC 的相对相位. 通过计算这些算符的期望值, 可以对上述算符的物理性质进行定量分析.

因此, 原子和光的整体初始态可以表示为

应用演化算符来精确求解系统的动力学

即将公式 (9) 演化算符作用到初始态 |ψ0〉. 公式(9)中gt为原子-光耦合时间强度, 其中t表示时间.

将公式 (4) 中的转换代入公式(10), 展开可得

其中,

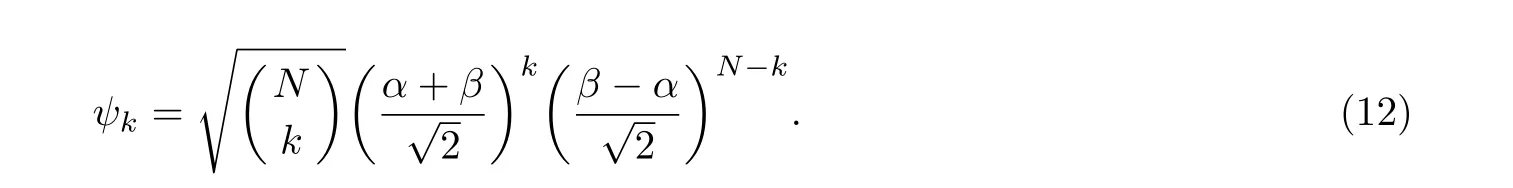
此时的Fock 态形式是将 |ψatom〉态拓展为定义在Jx基矢 |k,N-k〉上的广义态, 利用的是

另外, 干涉仪两臂的激光的量子态可以表示为相干态的形式 |αPh〉=|αl〉|αr〉. 通常将相干光表示为

其中, s=l,r , 代表干涉仪的左(left, l)右(right, r)两臂.

因此, 同时考虑BEC 原子和光的初始态, 可用态 |ψ0〉来表示, 即

此时, 由演化算符不难求得态随时间的演化, 可以表示为

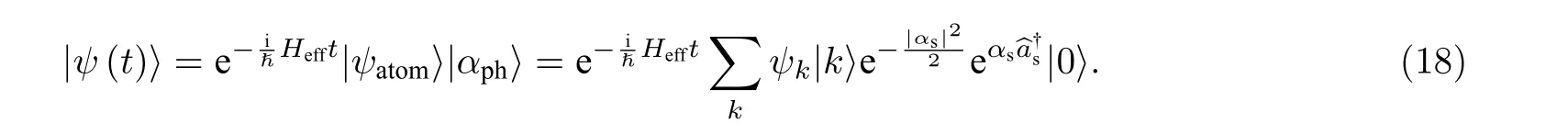
利用等式 eiθa†a|α〉=|eiθα〉, 可以将态(公式(18))进一步写成

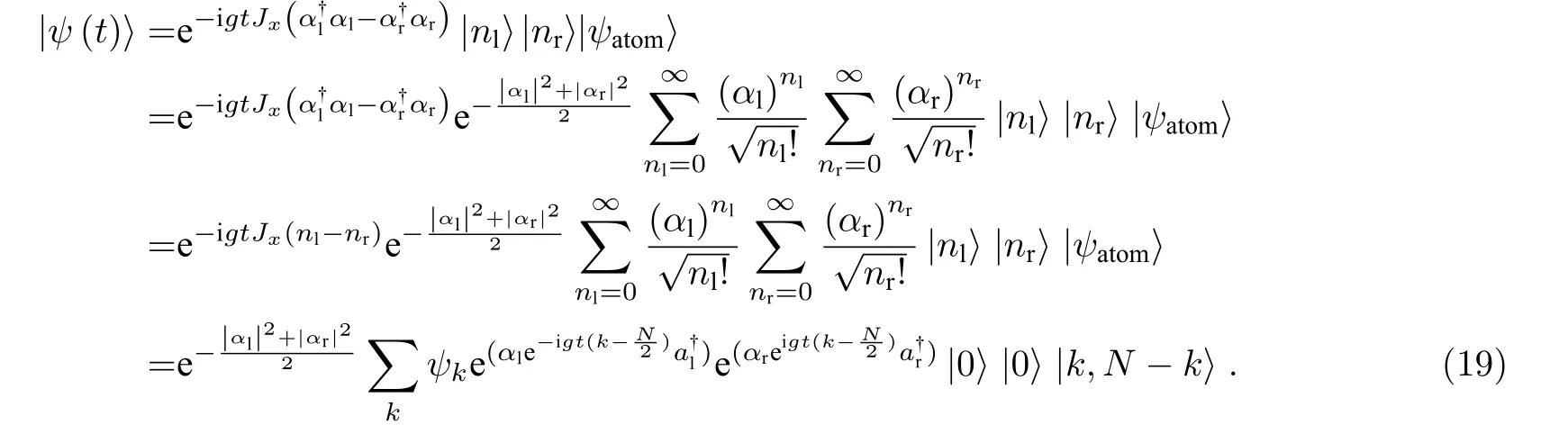
左右势阱中的光分别通过BEC 后, 在图1 所示的分束器(Beam Splitter, BS)上重新组合, 此时的光学模式转变为

因此, 通过测量相对光子数得到的相关物理性质可以存储在光子的光学模式c 和光学模式d 中.

将光模式的转换(公式(20))代入态中, 可以得到经过分束器(BS)后的态, 其形式为

其中,

最后, 当光通过分束器后, 分别探测处于光学模式c、光学模式d 这两个传感器中的光子数, 相当于对态 |ψBS〉进行投影测量. 投影算符为

通过投影算符计算, 可以得到

其中, 归一化系数

2 结果与分析

在得到上述光子测量后的BEC 的表达式后, 本文对不同基上的条件概率分布、Q函数进行了分析, 以便更好地研究其物理性质.

2.1 条件概率分布

图2 不同时间下在 |k〉 基矢上检测到原子的条件概率分布Fig. 2 Conditional probability of finding the atoms in the state |k〉 at different times

根据图2 中α,β的取值, 并利用二项式系数近似可将ψk近似为

基于本文测量后的BEC, 需要将Jn算符的本征态 |k〉转换到Jn算符对应的Fock 本征态 |k〉n. 运用公式(28)和公式(29)可以求得

图3 不同时间下在 |k〉x,|k〉y 基矢上检测到原子的条件概率分布Fig. 3 Conditional probability of finding the atoms in state |k〉x,|k〉y at different times

2.2 Q 函数分布

利用准概率分布可以将测量后的BEC 的波函数形象化, 而借助Q函数可以以一种简单直观的方式来观测BEC 的状态变化. 图4 给出了不同时间下测量后的BEC 的条件Q函数. 此处利用Bloch 球将其可视化,Q函数为

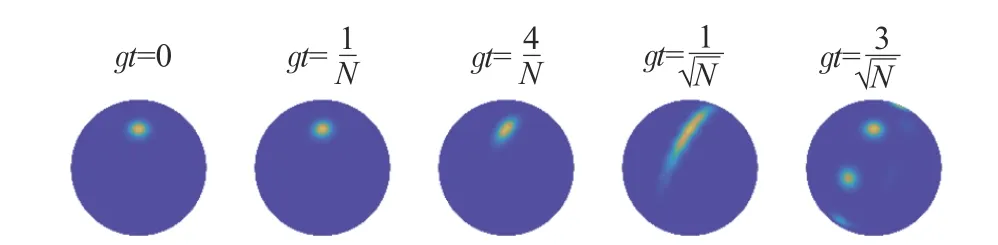
图4 不同时间下测量后的BEC 的条件Q 函数Fig. 4 Conditional Q function of the BEC measured at different times

2.3 自旋压缩判据

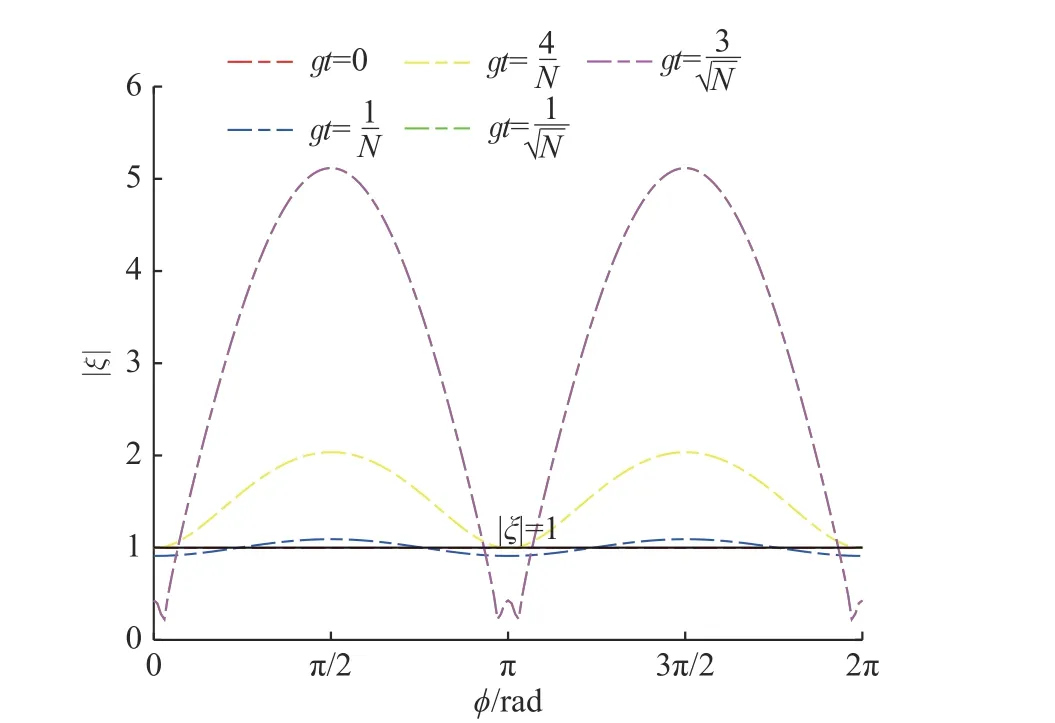
图5 不同时间下自旋压缩判据 ξ 随角度 φ 的变化Fig. 5 Variation of the spin squeezed criterion ξ with angle φ at different times

3 结 论

本文主要研究了在双势阱中制备BEC, 并进行非破坏性测量, 监测原子-光系统经非破坏性测量后, 随着原子-光耦合时间强度 (gt) 开始增大时, 能否产生压缩态和纠缠. 物理模型相较以往物理模型的优势在于, 本模型考虑了原子在两势阱中的隧穿. 本文工作的主要特点是, 采用精准波函数方法求解了量子非破坏性测量后的哈密顿量的动力学方程, 通过概率分布和Q函数分布可以更直观形象地观察BEC 态的演化, 结果表明, 当原子-光耦合时间强度gt ≪时, 非破坏性测量后的BEC 存在压缩态; 但是本文分析的连续测量所考虑的实验参数较少, 因此可能存在缺陷和噪声.