广义的变限积分函数求导公式证明及其应用
2022-07-28王瑞星徐清华吴克坚
王瑞星, 徐清华, 刘 烁, 吴克坚
(空军军医大学 基础医学院,陕西 西安 710032)
0 引言
变限积分函数及其导数作为高等数学定积分的一个重要知识点,本质是为了说明任何连续函数总有原函数存在,并由此引出高等数学中极为重要的微积分基本定理,从而将微分与积分紧密地结合起来。但是查阅《高等数学》[1]教材以及数学专业的《数学分析》[2]教材,发现针对变限积分函数及其导数,大都只说明了变上限积分函数的物理意义和几何意义并给出这类函数的求导定理及其证明过程,对于一般化的变限积分函数及其求导并没有具体讨论。然而,在实际教学与历年竞赛、考研题目中,对于变限积分函数的求导经常是考察的重难点,同时也是困扰学生的一个大难题。尤其对于变限积分函数的一般化求导公式,虽然公式形式简单,但是学生记忆起来比较困难,不易理解公式原理,不知如何推导。为此,周少波等[3]讨论了含参量的变限积分函数的求导公式,但最终给出的求导公式是
仔细观察这个公式,发现公式的右边β′(x)f(β(x),t)和α′(x)f(α(x),t)应该是β′(x)f(x,β(x))和α′(x)f(x,α(x)),而不应该再有t的出现,因为公式左边是对t进行积分。吕纪荣等[4]给出的求导公式也存在同样的问题,但他们的证明过程是完全正确的。张磊等[5]也分析了变限积分函数的求导问题,而他们直接应用了微积分基本公式给出了相应的证明过程,与教材中这部分内容的编排顺序不相符合,不利于学生的理解。宋传静[6]比较系统地总结了变限积分函数由易到难的求导公式,但是对于公式并没有作推导与证明。本文针对此类问题,给出变限积分函数更为一般化的求导公式,然后根据导数的定义给出了详细的证明过程,并重点结合部分考研、高数竞赛题目分析了其如何应用,便于学生学习掌握。
1 积分上限函数的求导公式
定理1[1]如果函数f(x)在区间[a,b]上连续,那么积分上限的函数
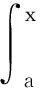
在[a,b]上可导,并且它的导数
证明详见《高等数学》教材[1]。
定理1的本质是说明连续函数总有原函数存在,并且其变上限积分就是其原函数之一,同时也揭示了定积分与原函数之间的联系。在实际教学中,教师还应该结合积分上限函数的物理意义和几何意义进一步分析讲解,以便于学生加深理解。
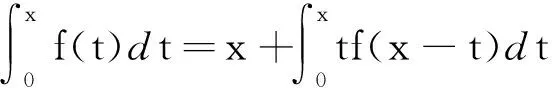
解首先利用换元法对方程右边的积分进行简单变形,令x-t=u,则
利用定理1,对方程两边同时关于x求导得
(1)

2 广义的变限积分函数求导公式
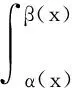
F′(x)=f[β(x)]β′(x)-f[α(x)]α′(x)。
证明由导数的定义可知,
再由
根据积分中值定理,存在0≤ξ≤1、0≤η≤1使得
所以有
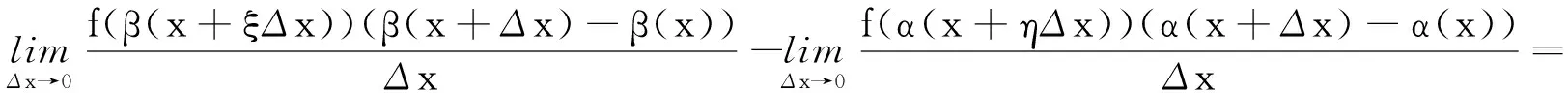
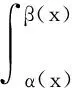
3 广义的含参变量的变限积分函数求导公式
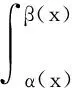
证明由导数的定义可知,
再由
及定积分的可加性得
根据积分中值定理,存在0≤ξ≤1,0≤η≤1使得
f(x+Δx,β(x+ξΔx))(β(x+Δx)-β(x))-f(x+Δx,α(x+ηΔx))(α(x+Δx)-α(x)),
所以有
由于α(x),β(x)在区间[c,d]上可微,二元函数f(x,t)在区域D上连续,因此当Δx→0时,有
综上可得
至此,发现定理1和定理2的结论公式其实都是定理3的特例。定理3的求导公式更为一般化,可以囊括大部分变限积分函数的求导问题,适用范围更广一些。在实际教学中,根据学生的掌握情况,应该对这部分知识点在教材的基础上做必要的拓展与说明,让学生能更加轻松应对不同类型的题目。
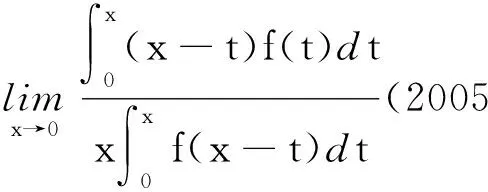
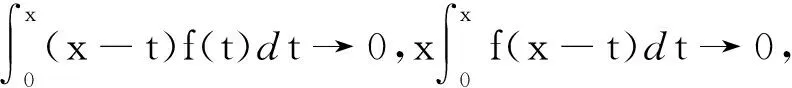
所以
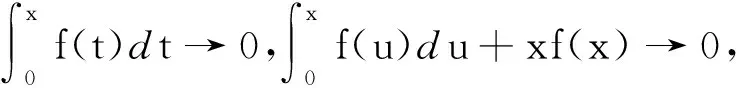
解2这里不再利用换元法,直接用洛必达法则和定理3得
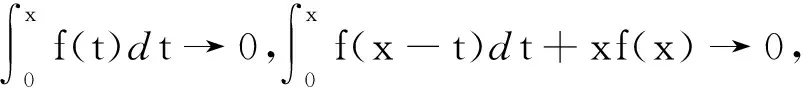
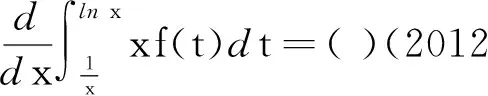
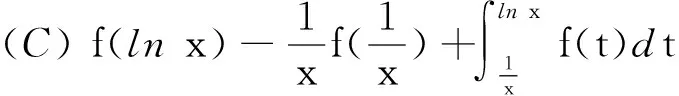
解1利用定理2得
解2直接利用定理3,得
因此本题正确答案是A。
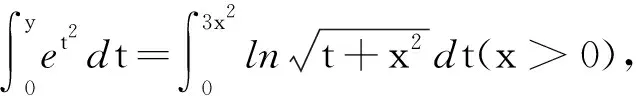
解利用定理3,将y看作x的函数,然后对
两边同时关于x求导得
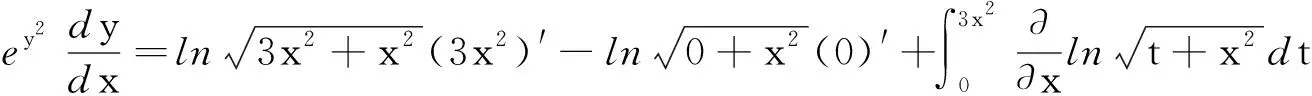
所以,
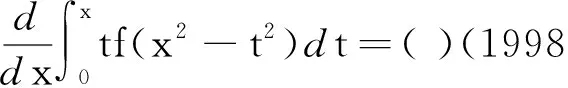
解1首先利用换元法,令u=x2-t2,则
du=d(x2-t2)=-2tdt,
替换上下限和被积表达式,得
利用变限积分求导公式得
解2上面的解题方法用到了换元法,然后利用了定理2的结论,这里可以直接利用定理3得
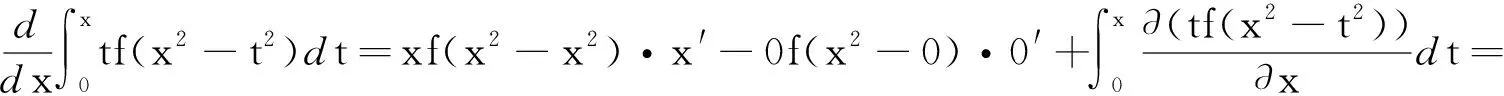
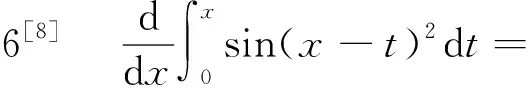
解1首先利用换元法,令u=x-t,则
du=-dt,
解2上面的解题方法用到了换元法,然后利用了定理1,这里可以直接利用定理3得
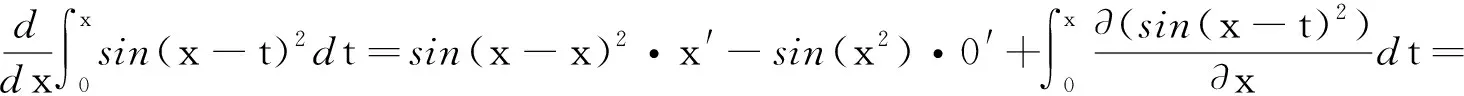
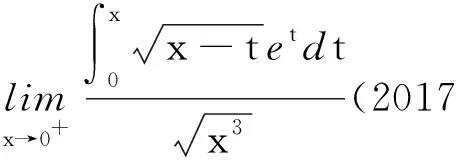
解1首先利用换元法,令u=x-t,则
du=-dt,
由洛必达法则,得
解2解1用到了换元法,然后利用了定理1,这里可以直接利用定理3和洛必达法则,得
从上述历年考研、竞赛题目的求解过程可以看出,如果能掌握定理1、2、3,就可以比较轻松地应对这类型题目,快速找到求解思路,而且也会大大简化求解过程,这也从一定程度上反映出变限积分函数求导公式的重要性。
4 结论
变限积分函数作为一类特殊函数,其求导问题一直倍受考研、各类数学竞赛的关注,而这一类函数的求导问题往往是学生的一个学习难点,也是教学中的一个重点。考虑到现行教材中对这部分知识讲解的深度与广度,本文基于教材的指引,将变上限积分函数的求导公式进一步推广到广义的变限积分函数的求导和广义的含参变量的变限积分函数的求导,并基于导数的定义给出了详细的推导证明过程,最后辅助部分考研、竞赛题目,说明了广义的变限积分函数求导公式的具体应用。对变限积分函数的求导进行了更深层次的探讨,有助于学生理清这部分知识点的脉络,提升对变限积分函数求导的宏观把握,同时也可以帮助授课教师对这部分知识点进行归纳整理,进一步提升授课质量。
