关于薄利多销问题的建模分析

韦碧鹏，黎会兰，蒙 仁

（1.柳州职业技术学院，广西 柳州 545006；2.北部湾大学，广西 钦州 535011）

0 引言

为了增加商品的销量，通过降低商品的价格来增加利润的方式简称为“薄利多销”。在现实生活中，很多商家都是通过这种策略来扩大销售的。根据弹性分析理念，如果商品价格下降，那么富有弹性商品的需求量将会增加，其增加的幅度将会大于商品价格下降的幅度，从而使得所产生的利润增加，“薄利多销”的方式在实际生产经营活动中已经被广泛应用。本文以2019年全国大学生数学建模竞赛E题为例，对“薄利多销”所产生的问题进行分析和研究。

问题一：问题中给出了商场2016年11月30日到2019年1月2日（以下简称“促销时间”）的销售流水数据，计算其每天的营业额和利润率（注意：由于复杂因素的影响，所得到非打折商品成本价的数据是不完备的，一般情况下，零售商的利润率为20%～40%)。

问题二：根据对题目的理解，建立合适的指标和商场打折力度的数学模型，并对商场促销时间每天的打折力度进行计算。

问题三：运用题目所给数据，分析打折力度与销售额、利润率之间的关系。

问题四：在问题三的基础上，根据商品的大类进行区分，分析打折力度与销售额、利润率之间的关系。

1 问题一模型的建立与求解

1.1 原始数据的预处理

问题一要计算出商场每天的营业额和利润率，首先要建立数据匹配的数学模型，运用SQL Server2014软件[1]把促销时间的商品销售流水记录表进行整合，得到销售流水记录原始表，共1221855条数据。通过观察销售流水记录表，发现销售流水记录原始表不属于完备的数据，存在着不完备的数据现象。一方面，销售记录原始表中存在着顾客未完成的订单数据（96664条数据），这些数据对于问题的处理没有任何意义，因此，需要对未完成订单数据进行剔除。另一方面，销售流水记录原始表中存在着大量的商品成本价格缺失，缺失数据占总数据的64.1%。舍弃这些数据对结果的准确性将造成较大影响。经过对问题和数据进行研究，本研究将对成本缺失数据进行修复，其中数据缺失情况分为以下三种：单件商品销售记录中从未出现过成本价；单件商品销售记录中出现过成本价，但仍存在成本价缺失；单件商品销售记录中没有成本价缺失。

针对以上三种情况，研究使用SQL Server2014软件将从未出现过成本价的数据、出现过成本价但仍存在成本价缺失、没有成本价缺失的数据分别取出，得到从未出现成本价表、出现成本价表、未缺失成本价表，接着对从未出现成本价表、出现成本价表进行以下处理[2-3]。

对出现过成本价的商品以成本价为目标，对数据进行去重，得到商品出现过成本价的信息，再根据成本价信息求出利润率的均值，以利润率均值为标准，计算并填充相同商品中成本为空的数据。

对从未出现过成本价的数据，将以相同的门店价利润率为指标，对未出现过成本价的数据进行成本价计算并填充；对存在的有效打折商品，按促销开始时间和结束时间为条件，商品编号为表示与销售记录表中的数据进行匹配，发现还存在有113条数据成本价为空，即可用折扣信息表在促销时间内对应的商品成本价填充，且将门店价、销售价及成本价之间不合理的数据进行剔除（如成本价〉门店价）。

1.2 商场营业额和利润率的模型与求解

使用SQL Server2014软件将处理后的从未出现成本价表、出现成本价表以及未缺失成本价表进行整合，最终得到完整销售记录表，总共1125132条数据，接着为计算出商场每天的营业额和利润率建立营业额和利润率相应的数学模型，分别如下。

营业额数学模型：

利润率数学模型：

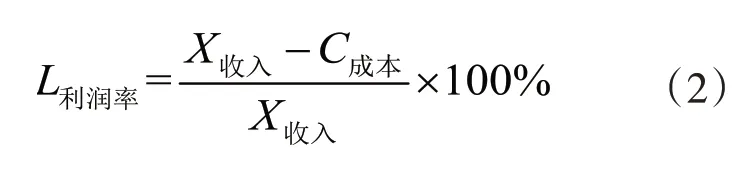
根据模型（1）和模型（2），运用SQL Server2014软件进行计算，得到每日营业额表和每日利润率表，见表1所示。

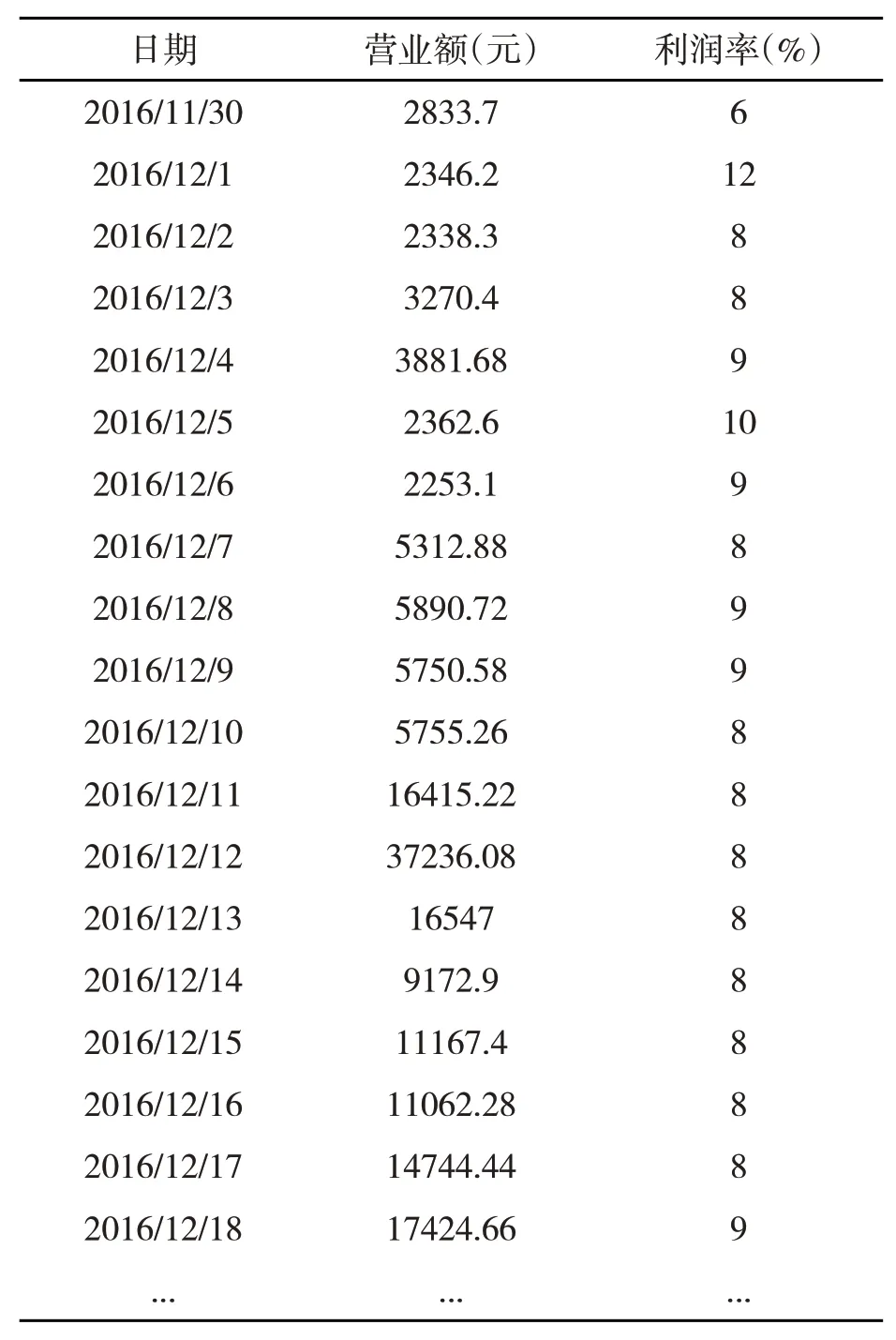
表1 商品每日营业额表和每日利润率表

2 问题二模型的建立与求解

针对问题二，要计算商场促销时间每天的打折力度[4-5]，首先需要建立单件商品打折力度的数学模型，具体如下。

单件商品打折力度数学模型：

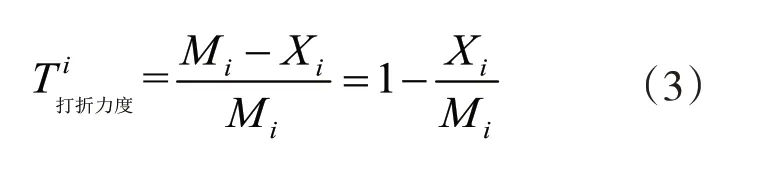
由于商场每天销售的商品种类繁多，因此，要计算出商场每天的打折力度，有以下几种方法：第一，计算出总的商品销售额和总的商品门面价格，运用模型（3）进行求解，从而得出每天商场的折扣率；第二，运用模型（3）把每天商场销售每种商品的折扣率都计算出来，然后对其求平均值；第三，考虑商品的属性不一样和顾客的偏向问题，采用线性加权的方法，建立多个商品打折力度的数学模型，接着运用问题一原始数据预处理所得到的完整销售记录表，从而得出每天商品的打折力度。

以上第一、第二种方法没有考虑到商品的属性不一样和顾客的偏向问题，因此，采用线性加权的方法，建立多个商品打折力度的数学模型，具体如下。

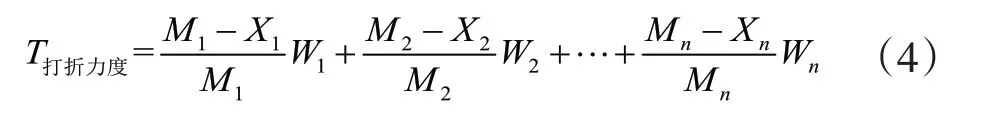
其中T打折力度表示每天商场的打折力度，Mi表示第i种商品的门面价格，Xi表示第i种商品的销售价格，Wi表示第i种商品的顾客偏好（即权重）。

结合模型（3），可以把模型（4）变为：

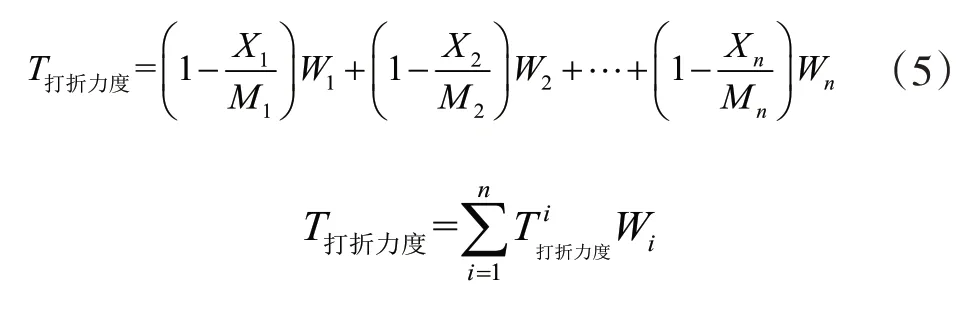
为计算出每天的打折力度，根据顾客的偏好，本研究以顾客购买第i种商品的数量与当天商品销售总数量之比作为第i种商品的权重值，基于此，模型（5）可改进如下：

其中，Si表示第i种商品的销售数量，S表示当天商品销售的总数量。

运用问题一原始数据预处理所得到的完整销售记录表，结合模型（6），可以得出商场促销时间每天的打折力度，具体如表2所示。

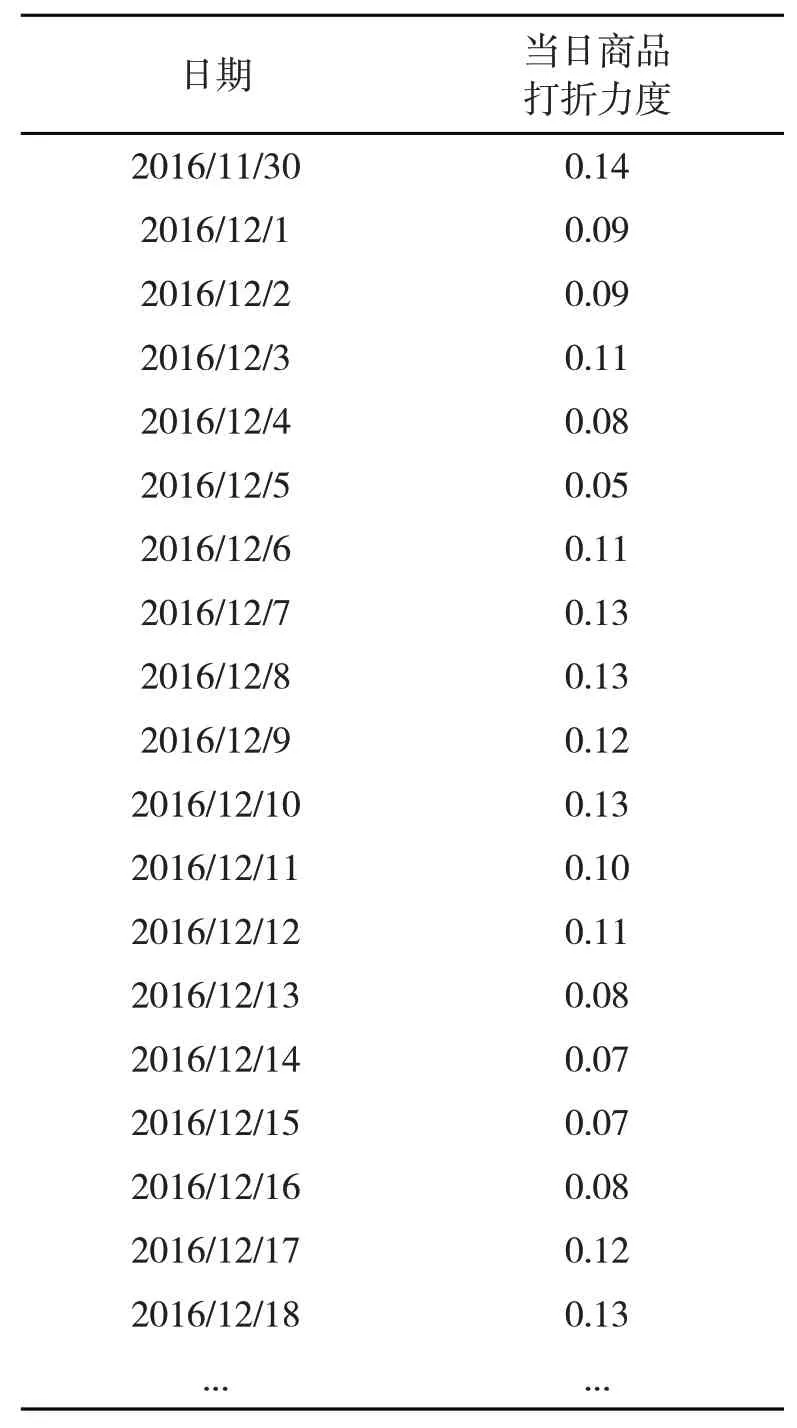
表2 每天商场的打折力度

3 问题三模型的建立与求解

针对问题三，分析打折力度与其他两个因素销售额与利润率的关系，以便从数据中挖掘出其隐含的信息。按照每天商品和单件商品两个角度进行分析，对打折力度、销售额以及利润率之间的关系进行相关性分析和线性回归拟合，最后运用随机数据和神经网络模型验证所得模型的正确性。

3.1 每天商品角度分析

通过运用SQL serve2014软件计算并筛选每天打折力度、每天商品销售额、每天利润率的数据，得到每天打折信息表（736条数据）。将每天打折信息表导入SPSS软件，使用皮尔逊相关系数[6]进行分析，得到如下结果。

皮尔逊相关系数：

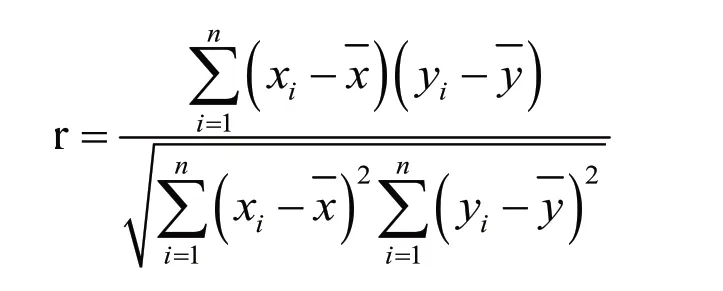
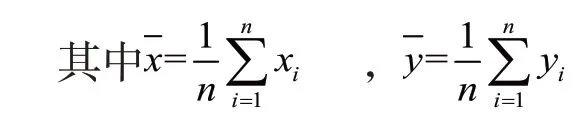
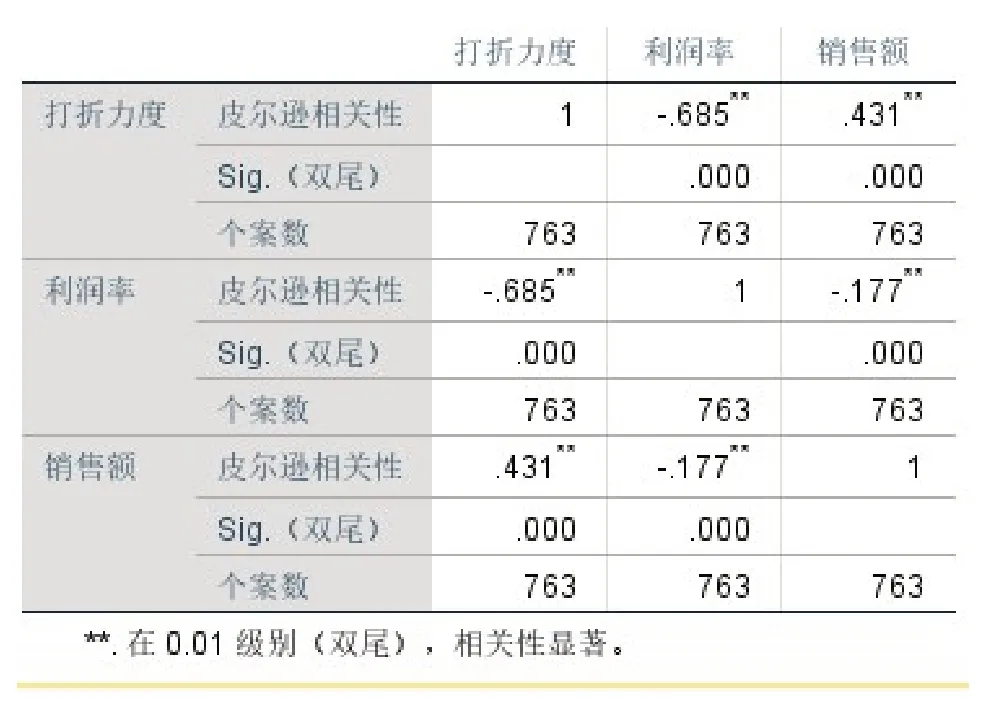
表3 每天商品打折力度、销售额以及利润率的相关性

从表3可知，每天商品的打折力度与商品利润率的皮尔逊相关性值为-0.685，它们具有负相关性，每天商品的打折力度与商品销售额的皮尔逊相关性值为0.431，它们存在着一定的关联。通过观察每天商品的打折力度、商品利润率以及商品销售额的显著性关系，发现它们之间存在着非常显著的关系。基于此，本研究运用回归分析法建立相应的回归分析模型[7]，具体如下。

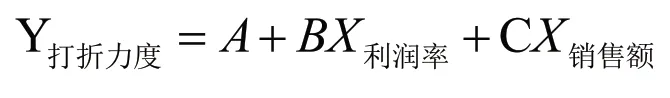
将每天打折信息表导入SPSS软件中，运用回归分析中的逐步回归分析法对数据进行拟合，得到每天商品的打折力度、商品利润率以及商品销售额的关系模型：

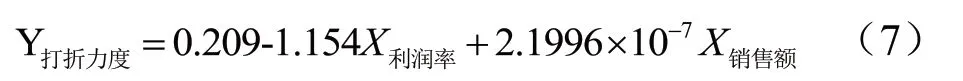
为检验模型的正确性，随机抽取50条样本数据对模型（7）进行检验，结果如图1所示。

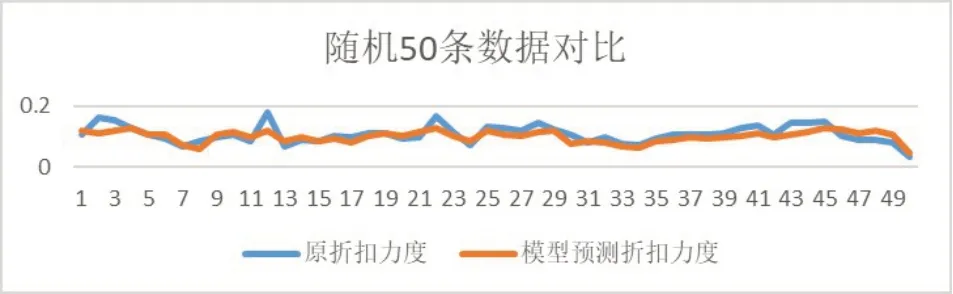
图1 模型（7）预测值与真实值数据对比

通过图1检验结果可知，研究建立的模型（7）通过了检验，即模型（7）能够表示每天商品的打折力度、商品利润率以及商品销售额的关系。

为进一步检验模型的正确性，研究运用神经网络模型对每天商品信息作进一步分析，使用python3.7编程语言调用tensorflow2.0建立神经网络模型，将每天打折信息表导入后，以销售额、利润率作为自变量，打折力度作为因变量，建立多元线性回归模型。初始化两个权重：model.add(layers.Dense(1,input_dim=2))，接着使用adam优化算法与均方差编译模型：model.compile(optimizer='adam',loss='mse')，将模型配置好后即可对模型进行数据训练。将每天打折信息表代入模型训练（model.fit(x,y,epochs=1000)），训练次数为1000。训练结束后发现模型的损失函数没有得到饱和的趋势，但是，已经被降到了很低的值，随机代入一条数据进行检测。

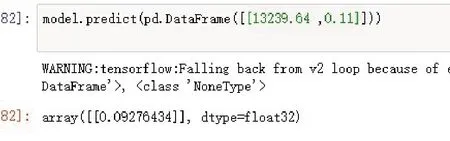
图2 神经网络模型对随机一条数据检测结果

由上图中可知，预测的打折力度为0.09276434，对模型作进一步检测，随机取10条数据，得出以下情况。

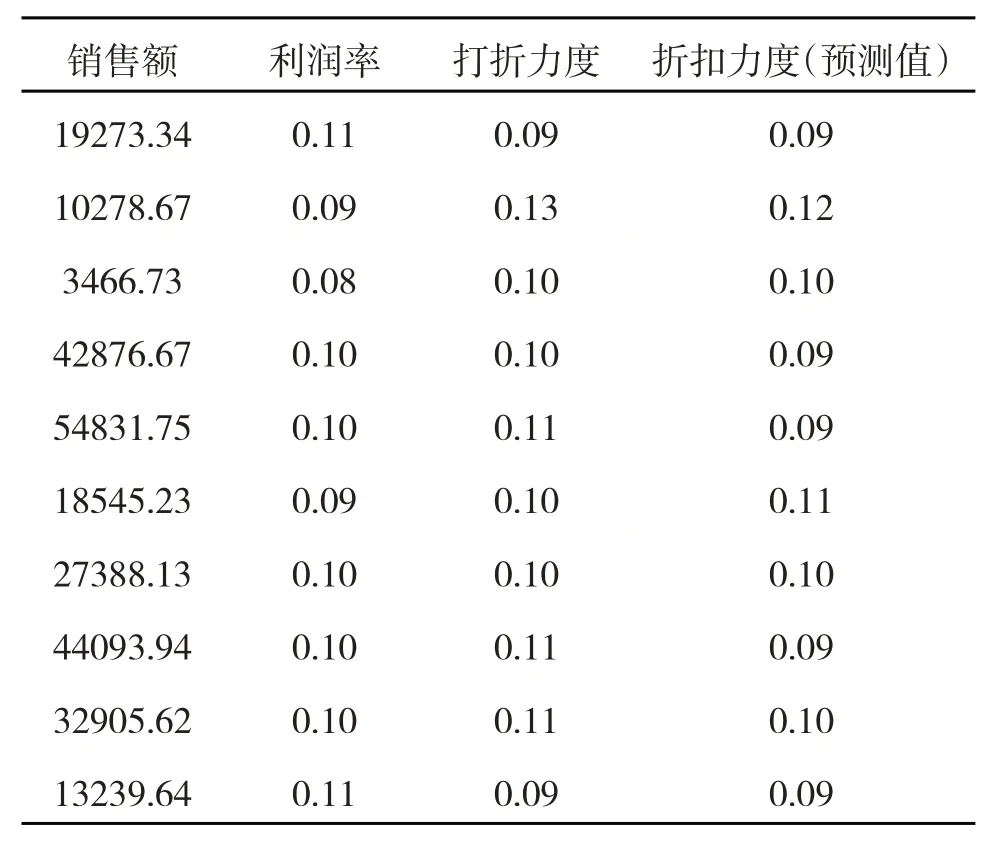
表4 神经网络模型对商品打折力度的预测值

从上表中，得到模型的预测值和真实值较为接近，即从另外的角度验证了模型（7）的正确性。

3.2 单件商品角度分析

与上述方法相同，运用SQL serve2014软件将每件商品的打折力度、商品销售额以及商品利润率的数据求出，将数据导入SPSS软件中，对单件商品的打折力度、商品销售额以及商品利润率进行相关性分析，得到如下结果。

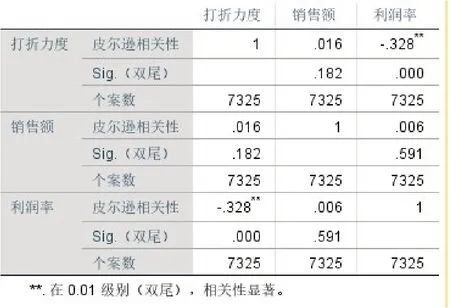
图3 单件商品打折力度、销售额以及利润率的相关性

从图3可知，单件商品的打折力度与单件商品利润率的皮尔逊值为-0.328，它们的关系呈负相关。单件商品的打折力度与单件商品销售额的皮尔逊值为0.016，其显著性大于0.01，显著性不强，基于此，研究对数据进行矩阵散点图分析，得到如下结果。

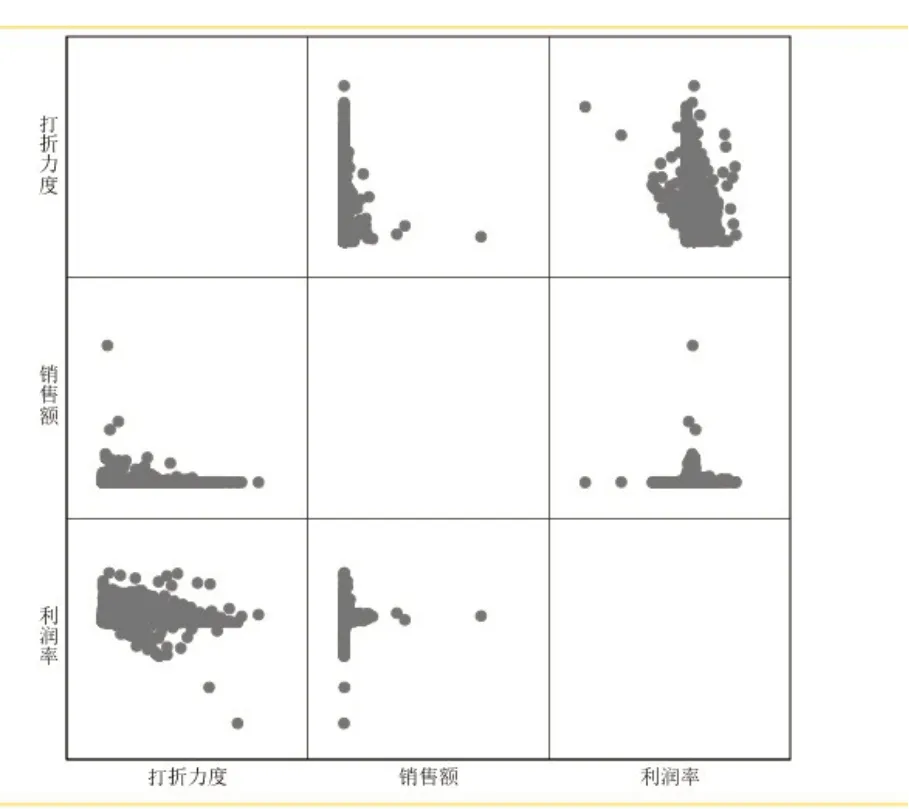
图4 单件商品打折力度、销售额以及利润率的矩阵散点图

首先，运用SQL Server2014软件对完整销售记录表的商品信息表以类目的形式进行匹配，从而得到各类目下的销售记录表。接着，从一级类目、二级类目和三级类目的角度分别对打折力度与销售额、利润率进行相关性分析，建立对应的关系模型。

研究先对数据进行处理，使用SQL Server2014软件求出每件商品的利润率、打折力度、销售额，得到每件商品打折信息表（共7325条数据）。接着，将商品打折信息表和商品的信息类目进行数据匹配，发现一些数据与商品的信息类目表数据无法匹配，即商品打折信息表中的一些商品信息查询不到。为得到完整的数据表，将舍去这些数据，最终得到以类目进行分类的数据（共6570条数据）。

从一级类目的角度分析商品打折力度、商品销售额以及商品利润率的关系，将一级商品类目数据表导入SPSS软件中，使用SPSS软件的相关性分析功能，对商品打折力度、商品销售额以及商品利润率进行分析，发现它们之间的相关关系不强。运用回归模型检验，发现它们之间的显著性指标过高，因此，得不到一个好的线性规划模型。

从二级类目的角度对其作相关性分析，发现商品打折力度与商品利润率的皮尔逊值为-0.519，具有负相关性。然而，商品打折力度与商品销售额没有相关关系，因此，运用SPSS对二级类目下的数据进行线性回归拟合，得到二级类目下的线性回归模型：

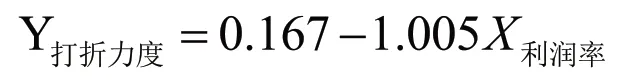
从三级类目的角度分析，与二级类目的角度分析结论类似。发现商品打折力度与商品利润率的皮尔逊值为-0.313，具有负相关性。然而，商品打折力度与商品销售额没有相关关系，因此，运用SPSS对三级类目下的数据进行线性回归拟合，得到三级类目下的线性回归模型：

从矩阵散点图可以看出，单件商品打折力度、销售额以及利润率的关系都没有呈现出明显的线性关系。

4 问题四模型的建立与求解

在问题三的基础上，根据商品的大类进行区分，分析打折力度与销售额、利润率之间的关系。

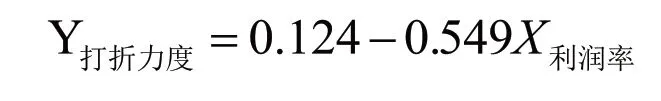
将二级类目下的模型、三级类目下的模型以及模型7进行对比，发现商品类目下线性回归模型的销售额显著性普遍偏高。随机抽取50条数据，将三个模型代入进行验证，将结果进行线性图绘制。

从上图中可知，二级类目下的模型与原模型的折线图幅度波动较为接近，二级类目和三级类目间的数据十分接近，因此，得出每天的商品打折力度对二级类目下商品的打折力度影响不大的结论。

5 模型的分析、推广及改进

5.1 模型分析

薄利多销模型的建立，有助于全国大学生数学建模竞赛工作的开展，对参赛学校和学生提高竞赛水平具有一定的参考意义，为学生掌握大数据分析技术奠定了必要的基础。薄利多销模型的建立和分析，操作性强，便于实现，在大数据时代应用价值高，对传统实体店的运营具有一定的指导意义。

5.2 模型推广

该模型以大学生数学建模竞赛为背景，问题为实际问题，根据商场的销售流水记录、折扣信息表以及商品信息表，分别建立了薄利多销的销售额、利润率以及打折力度的数学模型，分析它们之间的关系。模型可推广到各大商场和电商平台中，例如大润发实体店、天猫、淘宝、京东等。

5.3 模型改进

第一，在问题三中，检验所建立的模型正确性时，随机运用少量的数据对模型进行检验，虽然得到的结果比较好，但是，建议运用大量的数据对模型进行检验效果更好；第二，分析商品打折力度、商品销售额以及商品利润率之间的关系，如果能从时间的角度进一步分析不同时段商品打折力度、商品销售额以及商品利润率的关系，其所得结果和应用价值将会更好。

6 结语

薄利多销是商家扩大销售的一种策略。为了研究薄利多销的数学模型，本文结合2019年全国大学生数学建模竞赛E题进行研究，详细地对商场薄利多销的销售流水记录进行分析和建模，分别得到了营业额和利润率、商品打折力度、销售额及利润率的数学模型，且通过数据比较和神经网络方法验证提出模型的正确性和有效性，从而为商家促销提供数据依据。