数学问题解答

2022年4月号问题解答

(解答由问题提供人给出)

(浙江省慈溪实验中学 华漫天 315300)

证明分别过点A、点B作y轴与x轴的平行线交于点D，过点C作AD的垂线交于点E，易知△ABD≌△CAE，不妨令BD=AE=m，AD=CE=n，令A(asecθ,atanθ)，则

B(asecθ-m,atanθ-n)，C(asecθ+n,atanθ-m)，

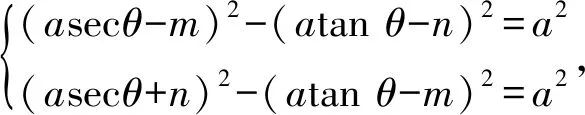
相加得2a(n-m)secθ+2a(m+n)tanθ=0，

相减得2a(n+m)secθ+2a(m-n)tanθ

=2m2-2n2，

得a[n+m+(m-n)sinθ]=(m2-n2)cosθ，②

①代入②并化简得

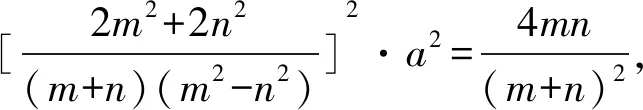
即a2(m2+n2)2=mn(m2-n2)2，

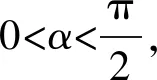
则a2d4=d6sinαcosα(cos2α-sin2α)2，

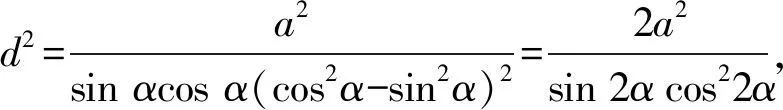
令sin 2α=t，则sin 2αcos22α=t(1-t2)=t-t3,

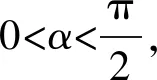
令f(t)=t-t3，则f′(t)=1-3t2，

从而sin 2αcos22α=t(1-t2)=t-t3

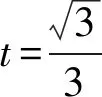
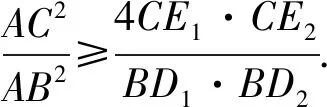
图1

(北京市第八十中学 徐红 100102)

证明如图2，延长CE1交AB于点F1，延长CE2交AB于点F2.

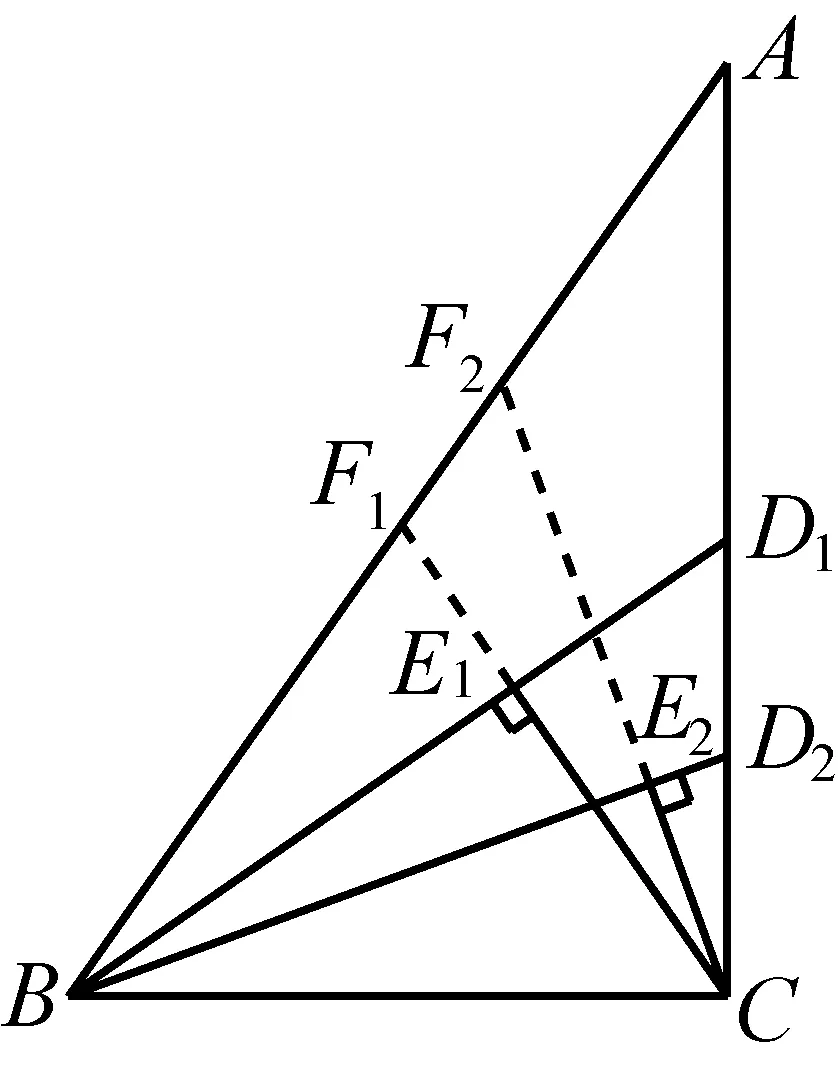
图2

因为∠ABD1=∠CBD2，

所以∠ABD2=∠CBD1.

所以Rt△BE1F1∽Rt△BE2C.

①

同理可知Rt△BE2F2∽Rt△BE1C.

②

由①×②得CE1·CE2=E1F1·E2F2.

③

因为∠BD1C=90°-∠CBD1，

∠BF2E2=90°-∠ABE2，

所以∠BD1C=∠BF2E2.

所以∠AD1B=∠AF2C.

④

同理可得△ABD2∽△ACF1.

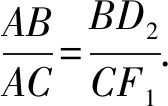
⑤

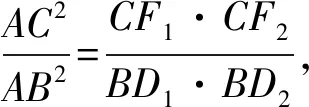
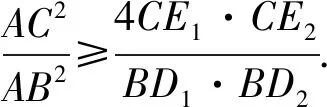
当且仅当∠ABC的内等角线BD1,BD2重合为∠ABC的平分线时，等号成立.

(安徽省无为中学 朱小扣 238300)

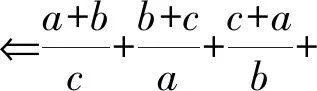
(1)式显然成立，故原不等式得证.

2659如图，已知在△ABC中，CD平分∠ACB，交AB于D，且(CD·AB)2=2CA·AD·DB·BC，求证：∠ACB=90°.

(江苏省溧阳市光华高级中学 钱德全 213300;江苏省溧阳市永平小学 张晓蔚 213333)

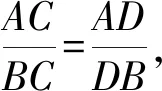
因为(CD·AB)2=2CA·AD·DB·BC，

所以(CD·AB)2=2(AC·BD)2，

由勾股定理的逆定理得∠CED=90°，

所以四边形CEDF为正方形，则∠ACB=90°.

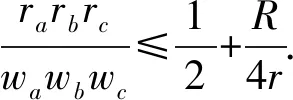
(安徽省南陵县城东实验学校 邹守文 241300)

证明设△ABC的三边长为a,b,c，面积为△，半周长为p，由旁切圆半径公式，

(p-a)ra=△=pr,(p-b)rb=△=pr,

(p-c)rc=△=pr，

由角平分线长公式

于是只需证明

因为a+b+c=2p,

ab+bc+ca=p2+4Rr+r2,

abc=4Rrp，

(a+b)(b+c)(c+a)

=(a+b+c)(ab+bc+ca)-abc,

于是上式又等价于

⟺p2+2Rr+r2≤4R2+8Rr.

由Gerresten不等式p2≤4R2+4Rr+3r2和Euler不等式R≥2r，有

p2+2Rr+r2≤4R2+4Rr+3r2+2Rr+r2

=4R2+6Rr+4r2≤4R2+6Rr+2Rr

=4R2+8Rr.

故所证成立.

2022年5月号问题

(来稿请注明出处——编者)

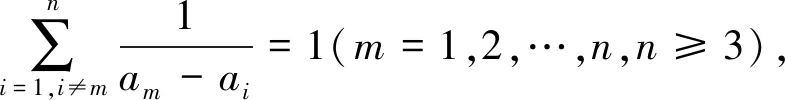
(浙江省海盐县元济高级中学 张艳宗 314300；北京航空航天大学图书馆 宋庆 100191)

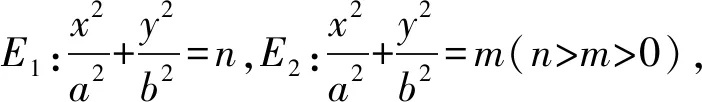
(四川成都七中 康盛 610041)

(江苏省木渎高级中学 孙国富 215101)

2664在四面体ABCD中，顶点A、B、C、D所对面的面积分别为SA、SB、SC、SD,以AB、CD为棱的二面角分别为〈AB〉、〈CD〉.求证：

(南京师范大学附属扬子中学 郝结红 210048)

(北京中学 史嘉 100028)