基于梯度优化的FAST反射面调节及接收比的研究

郭学俊，裴智明，靳谦诚，张 迪，李 雪

(太原理工大学 a.大数据学院，b.机械与运载工程学院，c.水利科学与工程学院，太原 030024)

依据FAST(Five-hundred-meter aperture spherical radio telescope)的反射面的调节机理[1]，全面构建主反射面的调节系统，通过研究解决从精度、速度等方面对其反射面进行深度的调节，解决实际工作中的问题，为我国的天体物理和数学模型的建立奠定基础。

目前在FAST主动调节的研究中，常用的反射板调节策略的预测方法有粒子群算法、支持向量机、遗传算法等等。张胜男[2]基于支持向量机实现了FAST节点位移预测模型，属于基于支持向量机算法在FAST节点位移预测的有益实践；端素红[3]采用粒子群算法解决了FAST主动反射面的整网控制问题；李明辉等[4]利用Matlab建立主索节点变位数值模型,对各种变形策略的主索节点位移量进行策略分析，对于提高主索网和反射面的调整精度意义重大；这些算法虽然各有优点，但FAST节点数目众多，节点位置数据量庞大，从而导致运算速度慢，计算程度复杂。因此，本文提出了一种基于梯度下降寻优算法的FAST主索节点及各促动器位置调节策略，更新速度快、可跳出局部最优到达全局最优。

目前对于FAST自主调节模型的建立局限于对点的模型，缺少基于促动器变形和反射面调整的动态变化调节过程，在评价策略上主要以节点运动参数、控制周期和索长精度来进行研究，缺少在馈源舱接受比的量化分析策略。

虽然我国大多数自然村村级财务管理工作采取了定期公开的制度，但是由于其公开的内容缺乏实质性，很多在内容上都属于空洞，因此不够具体。广大群众无法了解资金实际使用的用途，不能够有效资金进行民主的监督。同时整个资金管理意识较为缺乏，资金管理较为淡薄，特别是由于我国农村分散式的居住环境也导致了对村级财务管理工作的监督效果大打折扣。一些村民对于村集体的财务管理工作不够关心，缺乏相应的责任心，给了一些干部腐败以可乘之机，因此财务管理工作漏洞百出，很容易导致村级财务管理工作的腐败现象。

本研究对FAST(500 m口径球面射电望远镜)主反射面的调节和主索节点的运动调节建立有效的数学模型，采用梯度下降算法有效改善天体电磁波到达FAST馈源舱的接收效果。在对FAST馈源舱的接收面积与信号接收率的求解上，通过与费马原理的结合，将费马原理应用在光线三维空间反射方面，成功计算了三维空间内的反射光斑在馈源舱的反射接收情况，得出量化依据和量化参数法。经检验，在本模型当中得到的均方误差(Mean square)为0.308 9，说明FAST可以实现在某射波频段自如进行自主面调节的工作，并获得较高的馈源舱接受比。

合作社围绕竹林规模基地，确定了“集约化、效益化、品牌化”的发展目标。经营方向从原来的单一竹材经营向一二三产联动发展，通过发展毛料粗加工、林下经济、竹林旅游、竹林租赁等综合开发利用，有效提高了竹林地综合产出效益；经营方式从原来农户分散低效经营向规模高效经营转变，通过改变经营措施有效降低了竹材的生产成本，提高了竹材的规模经营效益。

1 一般位置理想抛物面的模型

1.1 一般位置理想抛物面的模型求解策略分析

首先，假设在特殊情况下，即被观测天体位于α=0°、β=90°，求解此时的最佳抛物面方程。将特殊位置的理想抛物面点按照面点分布律进行离散化，并确定离散空间各点的空间坐标(其中包括重要的主索节点的空间坐标)。

其次，利用旋转方程和转轴定理，综合特殊位置理想抛物面离散结果，可反求空间抛物面；求出被观测天体位于一般角度情况下，最佳抛物面的空间方程，优化了最佳抛物面的计算过程，降低了抛物面方程计算的复杂度，将计算过程简单化，应用更加广泛化。

最后，量化了理想抛物面下FAST馈源舱的信号接受比，并检验了本方案的主索网面调整方案的信号反射效果。

1.2 特殊位置理想抛物面的变形模型

假若FAST观测天体的位置在最特殊情况下，即α=0°、β=90°时(天体的方位描述以α、β量化描述为准，如图1所示)，需给出在满足实际工作条件

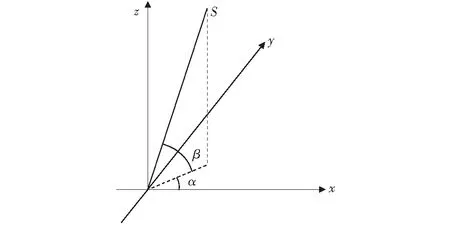
图1 天体观测的方位角和仰角示意Fig.1 A sketch of azimuth and elevation for celestial observations

下，FAST主反射面板调节约束条件下的理想抛物面位置，即相应形状，以此来指导以促动器为主的主索节点调节方式。

如图2，以球面(作为基准面)的球心为原点，可得球面和抛物面方程如式(1)所示：

(1)

其中，设定球面与抛物面口径相同均为R=300 m.

图2 特殊位置抛物面和基准球面的相互位置剖面示意Fig.2 Special position paraboloid and benchmark spherical position profile sketch

所以，良好的法律一定要根据不同政体来制定，因为不同的政体有着不同的公正。但是，我们思考统治与被统治的关系的正当状态时，也能发现上面讲的公正理念是合适的，各种政体都要能够吸收其要素，比如轮流为治的理念、按价值分配的公正理念、法治的理念等等。在形成了适合自己政体的法律之后，“恰当的法律可以拥有最高的权力。单一官员或某一些官员只是在法律无法详细涉及的事情上起裁决作用，因为任何普遍的论述都难以囊括所有的事实细节。”[2](P99)这的确是近代法律理论中官员自由裁量权的先声，其实也是法治理论的题中应有之义。

x2+559.2y+559.2×300.4=0 .

(2)

以标准方程式可做出空间内三维理想抛物面，其口径为300 m，最低点与基准球面相重合于一点。为清晰直观地观测理想抛物面与基准面的相互位置关系，以GRASP建立实时工作仿真模型如图3所示。

图3 GRASP建立实时工作仿真模型Fig.3 The real-time working simulation model is established in GRASP

根据基于解析几何理论的特殊位置建立的理想抛物面的优化变形几何模型，从直观上可以得知，其边缘处与基准圆面的光滑性越好，则调节难度越小，精度越大。反之，在衔接处会出现较大的拉压载荷，造成较大的应力，这就使得工作过程极其容易出现疲劳现象。通过对连接的光滑性和工作强度和疲劳性等影响因子进行综合考虑，在实际调节过程中就必须满足一定的约束条件才能使FAST真正高效的运行。

依据坐标变换矩阵M及特殊位置抛物面电磁波传播直线SC，带入式(8)，得到一般位置抛物面情况下，被观测天体和反射球面球心建立的电磁波传播直线方程SC为：

1.3 构建理想抛物面、特殊抛物面到一般位置抛物面的转化关系

(3)

其中，h′为理想抛物面沿Z′轴的偏移量的大小。

图4 设计抛物面的坐标系及转化坐标系Fig.4 Coordinate system paraboloid and transform coordinate system of desigh

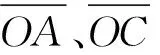
(4)

其中，i=1,2,…,692，代表筛选有效区域的有效点；j=1,2,3，代表空间坐标系的描述方式为三维空间坐标。

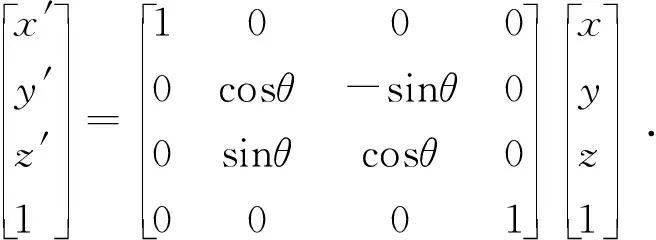
(5)

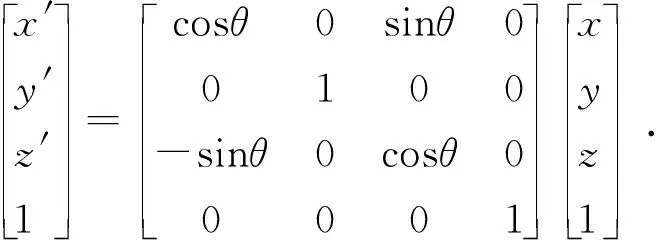
(6)

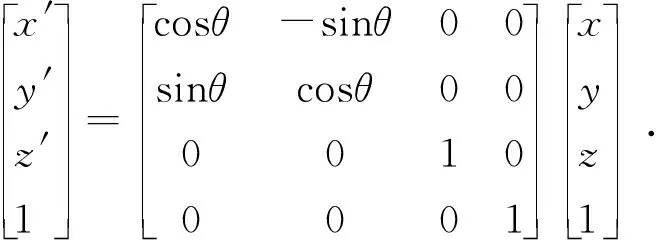
(7)

设天体观测的角度为α、β，例如在α=36.795°、β=78.169°的情况下，则可利用转轴公式得到单轴的空间旋转角度，如表1所示。

3.1 PBL和CBL基于MOOC概念的混合开放在线课程(MOOC)是指通过MOOC，使得不过在哪里都可以共享丰富的学习资源，包括关于超声医学相关课程内容的文本以及重要知识点的归纳。所谓MOOC概念的混合式教学法是指网络教学、LBL、问题学习PBL、CBL等在MOOC平台上的汇集成一个整体。它分为基础理论阶段和实践阶段。激发学生的兴趣爱好是第一阶段的侧重点。虽然LBL非计算机专业仍是目前教育模式的主体，但是在利用动态图像及视频等相关技术手段时，应当注意适度添加教师面部特征以及教师适中的语速，不仅能够提高学生对学习知识的积极性和兴趣，也可以让学生充分利用业余时间进行预习、自学和实践。

表1 利用转轴公式得到单轴的空间旋转角度Table 1 Inter rotation profit of shaft customs form

建立FAST一般位置的理想抛物面的主索网面优化变形的几何模型，步骤如下。

(8)

其中，M矩阵由式(5)-(7)，代入相应角度数值相乘即可得出：

1.4 一般位置理想抛物面空间解析式模型及其结果分析

从求出的特殊位置的理想抛物面出发，根据特殊位置抛物面上的离散点经过三维转轴旋转矩阵M变换后得到的空间面，经过全部主索节点的坐标拟合可得最终确定的一般情况下的抛物面解析式为：

0.001 740 0x2+0.001 760 0y2+0.000 075 2z2-
0.000 430 0yz-0.000 071 7xy-0.000 575 0xz-
0.164x-0.123y-0.979z=300.600 .

(9)

作抛物面方程的曲面图如图5所示。

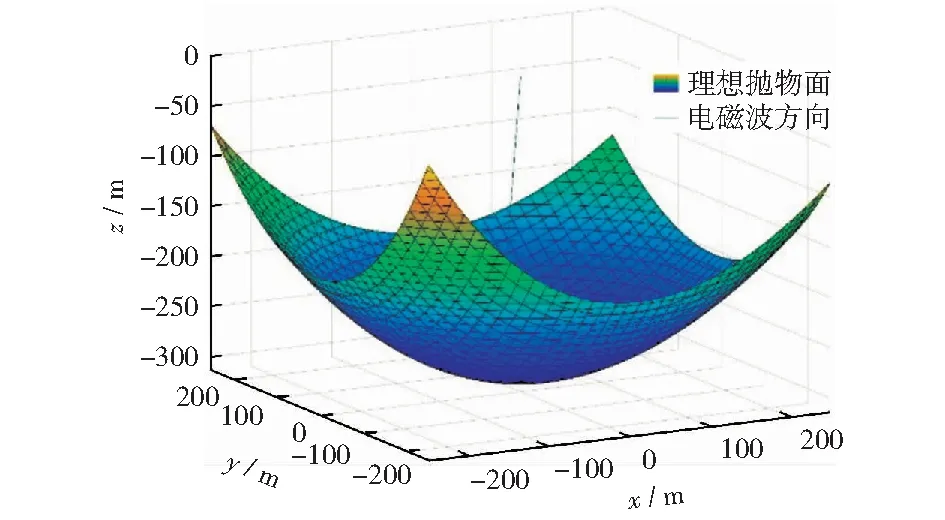
图5 一般位置的理想抛物面模型图Fig.5 Diagram of an ideal parabolic model in general position

当最低点的偏移距离h=0时，根据FAST调节设计要求，令F=0.466R，利用抛物线和旋转抛物面相关理论，利用Matlab工具得出理想抛物面的几何解析表达式为：

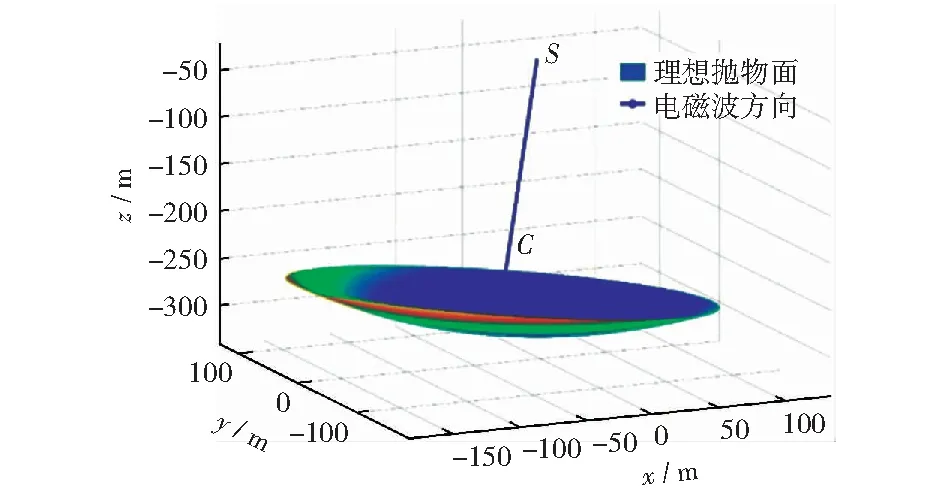
图6 一般位置的理想抛物面的位置形状Fig.6 General location of the ideal position of parabolic shape

经检验，三维理想抛物面与基准球面较好地实现了圆滑过渡连接，其形成的口径均为300 m.此次建模过程以GRASP(general responsibility assignment software patterns)进行模拟仿真[5]，建立实际状况下的工作效果图如图7所示。

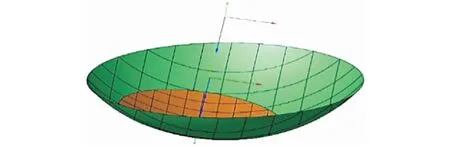
图7 GRASP下实际状况下的工作效果图Fig.7 Graph of work efficiency under GRASP solid state

众所周知，细胞增殖与凋亡两者之间的平衡是维持机体稳态的重要因素，其过程受到多种基因的调控，一旦基因表达平衡被打破，将导致疾病甚至肿瘤的发生发展。细胞增殖主要受细胞周期调控，是由多种信号通路共同参与的复杂网络调控过程。LncRNA SNHG16是近期研究LncRNA的新兴热点，国内外鲜有报道，目前发现LncRNA SNHG16在膀胱癌中高表达且与预后不良有关，可通过下调p21促进膀胱癌细胞的增殖［8］，但其在胃癌中的研究甚少，其作用机制也未研究透彻。

综上所述，hs-CRP检测在胎膜早破早产儿宫内感染早期诊断及感染程度分级中具有较高的应用价值，临床诊断时可与其他感染指标联合检测，以提高诊断灵敏度及特异度。

(10)

同时由一般位置抛物面与直线相交的空间理论，可由波的直线传播方程联立一般抛物面方程，可得一般抛物面方程顶点坐标O′(-49.319，-36.889，294.020)和抛物面焦点坐标P′(-26.336，-19.699，157.007).

素质教育和新课改中的先进教学理念其出发点和落脚点都是为了促进学生的发展，也就是说，目前小学数学的教育目标已经不是单纯的学生成绩与理论知识的累积，而是学生能力及综合素质的提升。小学数学情境教学就是教师在教学的过程中，有目的的创设或者构建具有情感色彩和身心体验的场景，激发学生的主观能动性和探究意识，实现知识的由繁变简，由抽象变具体的完美转化，进而提升“教”与“学”的效果。

2 一般位置的网面调整策略

2.1 建立目标最优的规划函数

模型建立过程充分考虑一般位置的瞬时抛物面的反射效果[6]，即令瞬时反射面更加贴近理想抛物面，则应建立两面贴合的距离函数，在若干约束条件下，使其结果达到最优。

依据关于促动器运动学的研究成果[7]，根据理论抛物面上的对应主索节点的位置坐标矩阵R(Rij)和在促动器位移调整变化之后的主索节点的位置坐标矩阵T(Tij)之间的距离的大小，可确定调节后反射面的空间坐标最优解，主反射面的结构功能关系示意图如图8所示，具体的规划函数如下：

(11)

图8 主反射面结构与功能关系示意图Fig.8 Schematic diagram of structure and function relation of main reflecting surface

2.2 构建约束条件

1) 根据FAST调节精度所限制的调节幅度[8]，促动器与下拉素的运动结构示意图(见图9)，反射面板调节后的任意两个相邻的主索节点的位置坐标间距G(Gij)需满足两者之间的距离浮动在位于0.07%浮动范围距离矩阵U(Uij)之内。

∀相邻Gij∈Uij.

(12)

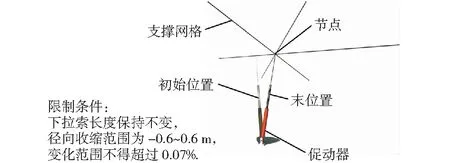
图9 促动器与下拉索结构示意图Fig.9 Structural diagram of actuator and lower cable

2) 根据制作要求，促动器的位移范围应当限定在(-0.6 m，0.6 m)之间。在运算中需要构建促动器的基准初始位置与调整后的促动器位置之间的距离关系，即反射面调节的促动器伸缩位移变化量N(Nij)，若在促动器移动为径向的前提下，其变化量近似与主索节点间距离的变化量相等，可构建约束式为：

(13)

若对于一般的空间主反射面，主反射面调节的促动器伸缩量变化值N(Nij)均应位于区间(-0.6 m，0.6 m)；具体的则由调节后的各主索节点对应促动器的上顶点位置L(Lij)与基准状态时促动器的基准位置M(Mij)间距进行表示。

3) 由于下拉索的材料性质决定其长度不可伸缩[9]，那么调节后的促动器上顶点的位置P与调节后的主索节点T的位置间距要满足下拉素长度为定值的约束。

(14)

2.3 综合构建促动器调节规划模型

由上述各约束条件分析，最终得出综合的数学规划模型如式(15)所示。

(15)

根据空间转化理论，空间的轴交角度在天体空间测量坐标系中进行三轴旋转后，得出最终的抛物面方程，其3个平面的单一投影旋转关系变换矩阵如下所示：

3 求解算法与结果讨论

3.1 梯度优化算法求解主索节点路径

(16)

在对FAST一般位置自主反射面变形的网面调整规划函数求解的过程中，为了最小化F(Ti)，亦即通过方向导数寻找下降迅速的方向，

印尼的华文教育在日本殖民时期遭到严重破坏。1942年8月1日，爪哇日军政监部批准华侨小学复课，学校以“华侨私立初等学校”为名称，日语是学校的必修课。日本政府以“东方国家崛起”为口号，为获取印尼各民族的认同，先后支持建立了“印尼独立筹备事务调查委员会(BPUPKI)”和“印尼独立筹备委员会(PPKI)”。此间，在努力推广日语的同时，处于合法地位的印尼语被广泛使用。与此相反，短暂的日本殖民统治毁灭了当时印尼的华文教育。日本殖民政府禁止华语在华校之外的地方使用，将华语的使用置于非法地位。

人是管理活动中最为关键的因素，管理人员素质的高低，直接决定了管理水平的优劣。从某种意义上来说，高校教学管理水平的竞争，实际上就是教学管理人员素质的竞争。一支高水平、高素质、相对稳定的教学管理队伍是大学教学质量的有效保证。然而，目前大学教学管理队伍普遍存在的专业能力不强、发展空间狭小等问题，已影响到大学教学管理组织效率与创新能力及大学教学水平的进一步发展。

(17)

其中ξ是与梯度的空间自然角。

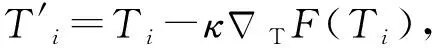
由训练误差曲线可以看出，两个CNN框架在训练迭代15 000次后误差已基本达到收敛，其中CNN-1收敛速度较慢，可能的原因是多尺度模块的引入，导致梯度在反向传播时计算量增加。由测试正确率曲线可以看出，在迭代约24 000次后，CNN-1的测试正确率已超过CNN-2，且正确率大小整体趋于稳定。

3.2 主索节点调节的结果参数

从促动器调节主索网反射面的理论出发[11-12]，再采用非线性规划策略对一般位置实现自主抛物面变形的网面调整策略模型，利用Matlab等工具对规划结果进行求解[13]，得出主索节点自主调节前后的主索节点各个位置坐标，并对调整到一般位置抛物面的对应促动器的伸缩量进行求解，其中部分调整后的主索节点的空间坐标，如表2所示。

四川竹编产品普遍存在制作周期长、产品更新速度慢等问题，在工业化潮流的冲击下慢慢失去市场竞争力，也很难招到愿意潜心学习的年轻学员，竹编技术面临技艺传承断层的困境。因此，政府应大力扶持竹编艺术家，帮助拓宽竹编艺术的发展空间，多组织一些关于竹编工艺及特色竹编制品的宣传活动[8]，唤醒人们对竹编行业的重视，让竹编艺术顺应新时代潮流，逐步融入现代社会。同时，竹编行业亟需加强市场管理，严厉打击劣质低等、假冒伪劣的竹编产品，维护四川竹编的行业信誉。

表2 部分调整后的主索节点的空间坐标(以与A1相邻的节点为例)Table 2 Spatial coordinates of partially adjusted main cable node (taking the node adjacent to A1 as reference) m

部分调整后的主索节点对应的促动器的伸缩量，如表3所示。

受篇幅所限，其余试验结果不一一列出。针对每种偏斜条件，跟据偏斜输入量，纠偏系统所给出的输出量均比较贴近实际人工纠偏操作，验证了纠偏算法的可靠性。

表3 部分调整后的主索节点对应的促动器的伸缩量(以与A1相邻的节点为例)Table 3 Expansion and contraction of the actuator corresponding to the partially adjusted main cable node (based on the adjacent section with A1)

3.3 馈源舱接收比分析

对于信号接收效果的分析[14]，该方案采用光线模拟的方法，利用费马原理[15]在光线三维空间反射方面的应用，计算三维光线的入射角、反射角、入射点等等，从而分析三维空间内的反射光斑在馈源舱的反射接收情况，其中空间电磁波在反射板上的反射情况，如图10所示。

图10 空间电磁波在反射板上的反射情况Fig.10 Reflection of space electromagnetic wave on reflector

可根据抛物面上反射到馈源舱的反射光线所投出的面积与所有镜面反射光线所投出面积之比求出馈源舱的接收比[16]；求出三角形小镜面边界处3个主索节点处的光线反射情况，得到小镜面反射的光斑面积。通过判断反射光斑是否经过接收器圆盘的圆心O，判断反射光线是否到达馈源舱。由于天体距离FAST很远，可以认为FAST的接收光线的近似方向为SC直线方向，其中，对应反射光线的反射方向矢量可以由费马原理求出，入射点即为主索节点。

对于小学生来说，在学习过程中他们遇到的最大的敌人应该是他们自己。这是因为小学生往往缺乏自制力，注意力没有办法长时间的集中，特别是对于那些不能够很好地调动起他们学习兴趣的东西，他们更是容易分神，导致学习效率低下，学习效果不佳。所以说，小学数学教师在进行课堂教学的过程中，首先要考虑的是如何调动学生学习热情的问题，尽可能地从学生的实际情况出发，在考虑课堂教学知识性的同时还要充分考虑学习过程的趣味性。这样，小学生才能乐于积极参与到课堂学习中来，身心也才能真正投入，学习也才能产出良好的效果来。

利用Matlab求解得接收比为1.43%，调整抛物面照明区域内反射面板数为1 295块，成功反射信号到达馈源舱的反射面板数量为1 295块，比率为100%.证明调整抛物面信号反射成功率极高，但由于馈源舱接收面积较小(3.141 5 m2)，单个反射面板平均面积较大(54.822 9 m2)，反射面板总面积较大(70 995.659 1 m2)，导致信号接收比较小。

根据费马原理求得主索节点处入射、反射光线、反射信号接收，如表4所示。

表4 主索节点处入射、反射光线方向、反射信号接收情况如下Table 4 Cable point entry and ray to anti signal connection, such as incident at the main cable node, reflected light direction and reflected signal reception are as follows

4 结束语

本文基于促动器调整反射网面的相互关联理论，采用非线性规划策略和寻优算法建立对一般位置实现自主抛物面变形的网面调整策略模型，以理想抛物面和调节后的主反射面的空间距离为衡量指标建立数学模型。根据相关资料文献显示，理想抛物面与实际工作面之间有一定的位置偏差，在衡量两者的偏差关系时将考虑两者的均方误差。经检验，在本模型当中得到的均方误差(Meansquare)为0.308 9，则可以认为FAST在此种主动调节的模式下可以平稳高效的工作。同时考虑并量化了FAST馈源舱接收比的影响，这一方案是对FAST主索网面的自我调节效果的有益检测和有效优化。