基于普通克里金法的同位素测氡探火数据优化处理

刘 轩，王俊峰，周 斌，刘 硕

(太原理工大学 a.安全与应急管理工程学院，b.山西省矿井通风与火灾防治工程技术研究中心，c.矿业工程学院，太原 030024)

矿井自燃火灾防治的关键在于火源位置的准确探测，基于不同的探测原理，国内外研究学者提出了不同探测方法，包括地表测温法、遥感法、同位素测氡法等[1]。其中，同位素测氡法是利用煤岩介质中天然放射性氡随温度升高析出率增加的特性，在地面探测氡及其子体的变化规律，并经过一系列数据分析处理，从而给出火源位置、范围及发展趋势。大量的灭火工程实践证明，该方法能够克服遥感法分辨率低及地表测温法反演计算复杂、不适合深部火区探测的缺点，是一种行之有效的非接触隐蔽火源探测技术[2-3]。

等值线图作为一种直观的图件，广泛应用于各种数据的分析处理之中，对于同位测氡法在地表有限测点所获得的氡浓度数据，其生成等值线图的关键是插值方法的选择。目前，主流分析软件中使用的插值方法是最小曲率法，该法通过构造穿过平面每一个数据点并具有最小曲率的曲线，进而组成氡浓度分布等值线图，并将图中的高值区域确定为火源位置。由于最小曲率法主要考虑曲线的光滑性加之测点数据量有限，因此形成的氡浓度分布失真，往往超过最大值和最小值的范围，与实际相差较大，进而影响火源位置的圈定[4]。事实上，地表氡具有空间分布的特点，即取值与所在区域内的位置有关且相邻测点间具有某种程度的自相关性，属于区域化随机变量的范畴，仅依靠最小曲率法无法在充分挖掘区域化随机变量所蕴含的结构性信息的基础上进行插值[5]。

目前，常用的单变量克里金插值方法包括简单克里金法、普通克里金法以及泛克里金法[6]。其中，简单克里金法假设区域化变量的数学期望是已知的常数，在实际应用中一般难以满足[7]；泛克里金法适用于存在某种漂移的区域化变量，该方法将插值过程分为趋势项和残差项两部分之和，但残差变异函数的预测较为繁琐，适用于煤矿可采储量预测等问题[8]；普通克里金法要求所研究区域化变量的数学期望为未知常数，该方法是目前应用最为广泛的插值方法，具有线性无偏、最优估计的特点，近年来已广泛应用于表层土壤磁学性质的研究[9]、地下水位和土壤湿度的采样分析[10]、浅源地震的重力变化特征延拓[11]以及矿井水文地质建模[12]等领域的研究中，均显示了良好的应用效果。

地理信息系统(geographic information system，GIS)技术中地统计分析模块集成普通克里金插值方法所需的探索性空间数据分析、变异函数建模等功能，是实现普通克里金插值方法的技术载体[13]。

笔者拟将地质统计学中普通克里金插值方法应用于同位素测氡探火数据的处理中，并将插值结果与最小曲率法所得结果进行比较，最终通过钻孔验证火源位置圈定的准确性，以期优化氡浓度数据的处理方法，最大程度提高同位素测氡法判断火源位置的准确度。

1 普通克里金法的理论基础

普通克里金法是以区域化变量理论和空间连续性理论为基础，以变异函数为基本工具，研究在空间分布上既有结构性又有随机性的地质变量，建立符合地质规律的统计模型来反映变量的变化规律，并对其空间分布进行预测[14]。

1.1 区域化变量

区域化变量Z(x)是以空间点x的3个直角坐标xu，xv，xw为自变量的随机场Z(xu，xv，xw).从其定义可以看出，区域化变量描述的现象具有空间分布的特点，地表氡浓度因其取值是与位置有关的随机函数，符合区域化变量的定义[15]。从另一个侧面反映出仅通过纯数学方法的最小曲率拟合，无法合理有效地预测地表氡浓度趋势。而区域化变量所具有的结构性和随机性特征需要通过变差异函数来表征。

1.2 变异函数

变异函数是区域化变量增量的方差，将区域化变量Z(x)在x，x+h两点处差值方差的一半定义为Z(x)在h方向上的变异函数γ(h)，其表达式为：

(1)

式中，Var代表方差。

而在实际工作中以试验变异函数来计算，其表达式见公式(2)：

(2)

式中：h为xi和xi+h两点的距离；Z(xi)和Z(xi+h)分别为xi，xi+h两点处的观测+6值；n(h)为相距h的数据对数目；γ*(h)为实验变异函数。

图1所示为理想的试验变异函数图。

图1 变异函数图Fig.1 Variogram function

图中有3个基本参数：

1) 变程a，用来度量空间相关性的最大距离，是变异函数达到稳定值时的空间距离。变程越小，区域化变量空间规律性变化的范围越小，该参数在该方向上变化越快，即非均质性越强；相反，变程越大，区域化变量空间规律性变化的范围越大，表明该参数在该方向上变化越慢，也就是非均质性越弱。

2) 基台值(C0+C)，是变异函数在变程处达到的平稳值，反映了研究范围内的变异强度。基台值越大，该参数在该方向上变化幅度越大，也就是非均质性越强；基台值越小，该参数在该方向上变化幅度越小，即非均质性越弱。

3) 块金值C0，是h=0时的变异函数值，反映了区域化变量的随机性大小[16]。

1.3 理论模型拟合

根据实测数据做出的试验变异函数图，实际上只是一条非光滑曲线，还需用一条适当的圆滑曲线对它进行拟合，并用特定的函数来表示拟合结果，即变异函数的理论模型，该模型将直接参与克里金插值。以最常用的球状模型为例，其表达式：

(3)

球状模型曲线如图2所示。

图2 球状模型曲线Fig.2 Spherical model curve

1.4 普通克里金法

普通克里金插值法对于任意待估点的估计值是通过该点影响范围内的n个有效样品值的线性组合得到，即

(4)

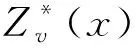
1) 无偏估计，即估计误差ε的期望值为0，可表示为：

(5)

2) 估计方差最小，见式(6).

(6)

在满足以上条件的同时，为保证权重系数λi有解，需要对区域化变量Z(x)的数学期望m的取值做出假设。不同克里金法的区别就在于所做假设的不同，普通克里金法要求Z(x)满足二阶平稳假设，即数学期望为未知常数m.整理得普通克里金方程组见公式(7).

(7)

该方程组有n+1个未知数(n个权重系数λi和一个拉格朗日乘数μ)和n+1个方程，可从方程组解出未知数值。综合以上步骤，普通克里金插值法的流程如图3所示。

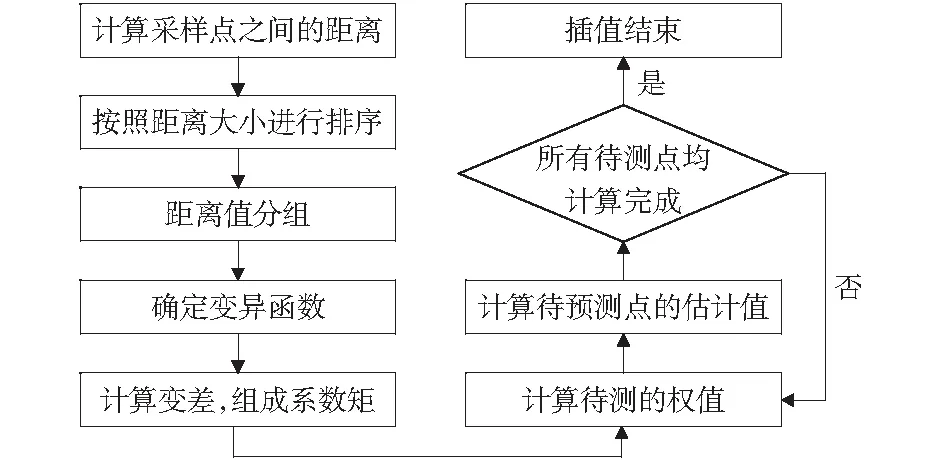
图3 普通克里金插值法流程图Fig.3 Ordinary Kriging interpolation flowchart

2 应用实例

2.1 研究区域概况

本文选取晋城煤业集团古书院煤矿张岭火区，着火煤层为3#煤层，该煤层较为稳定，厚度为0.6～0.9 m，埋藏较浅，仅为15～30 m；上覆岩层为厚约6 m左右的粉砂质泥岩，其上为中细粒长石英砂岩，厚度为15～19 m，砂岩上部覆盖有第四系上更新黄土。根据现场踏勘结果及井下采动影响区域，确定探测区域面积50 850 m2，采用HOLUX GR-260型手持GPS进行测点定位，以15 m为间距共布置234个测点，并使其均匀分布于整个探测区域，并在各个测点处使用α杯法对自燃危险区域的位置与范围进行探测。α杯法是将高吸附材料制成的α探杯倒置埋入土壤中，待杯内氡浓度与土壤环境中的氡浓度达到放射性动态平衡后(一般认为4 h以上即可)将探杯取出并放入CD-1α杯探测仪测量，由于吸附于探杯内壁上的氡子体与氡浓度存在线性关系，故可通过测量氡子体实现对土壤中氡浓度的测量。

探测原始数据为每3 min内氡及其子体衰变个数的计数值(N/3 min)，本区域氡射气底数为50 N/3 min.

2.2 异常值分析

对于测得的原始数据，需要对数据中存在的由于仪器震动、人为操作等造成的异常值进行剔除，并分析其产生的原因，如果不加剔除地把这些异常值包括进数据的计算分析过程中，会影响插值结果。

箱形图因其判断异常值的标准以四分位数和四分位距为基础，异常值不能对这个标准施加影响，所以常被用来观察数据中存在的异常值。箱形图中上、下边缘之间的部分称为内限，处于内限以外位置的点表示的数据为异常值，这里需要说明的是异常值是对数据中离群值点的统称，其所代表的意义是由使用箱形图的目的所决定的，在对测氡探火数据的分析中，异常值除显示需要剔除的测点外，还可表征火区范围内的测点。

这样的判断是基于煤自燃演化规律，由于自燃煤层长时间氧化蓄热致使温度上升，温度从火源中心点呈扩散状向周围环境依次递减，相应地表火区对应位置处氡浓度也呈依次递减的扩散分布，在箱形图上则表现为排列紧密的数据点[17-18]。图中孤立异常值点所处的氡浓度区间为1 441 N/3 min～1 817 N/3 min，共6个点，分析其产生的原因如下：

1) 将探测杯从埋坑中铲出的过程，会在周围产生一系列的冲击裂隙，在增加了土壤透气性的同时为氡的扩散提供了更多的运移通道。

2) 同样在该过程中，铲出的部分土壤会破坏其与大气之间已形成的压力平衡，造成空气对流而导致更多的氡涌向地面。

3) 仪器的晃动影响CD-1α杯测氡仪的稳定性。

以上过程均可使瞬时氡浓度急剧升高，导致孤立异常值点的产生，对这些测点重新测量后所形成的箱形图(图4)连续异常值浓度区间为464 N/3 min～743 N/3 min，即火区范围内测点的氡浓度所在区间。

图4 原始数据箱形图Fig.4 Radon counts boxplot

2.3 探索性数据分析

使用普通克里金法进行插值分析，为满足二阶平稳假设，首先要确保数据呈正态分布，否则需要根据分布情况对数据进行转换。

频率分布直方图因其能清楚显示各组频数分布情况又易于显示各组之间频数的差别，故可直观地反映出数据的分布状态。调用ArcGIS统计分析模块中的探索性数据分析功能，得到地表氡浓度数据的频数分布直方图。观察直方图呈“陡壁型”分布，如图5所示。表1为ArcGIS探索性数据分析所得的各项统计指标。

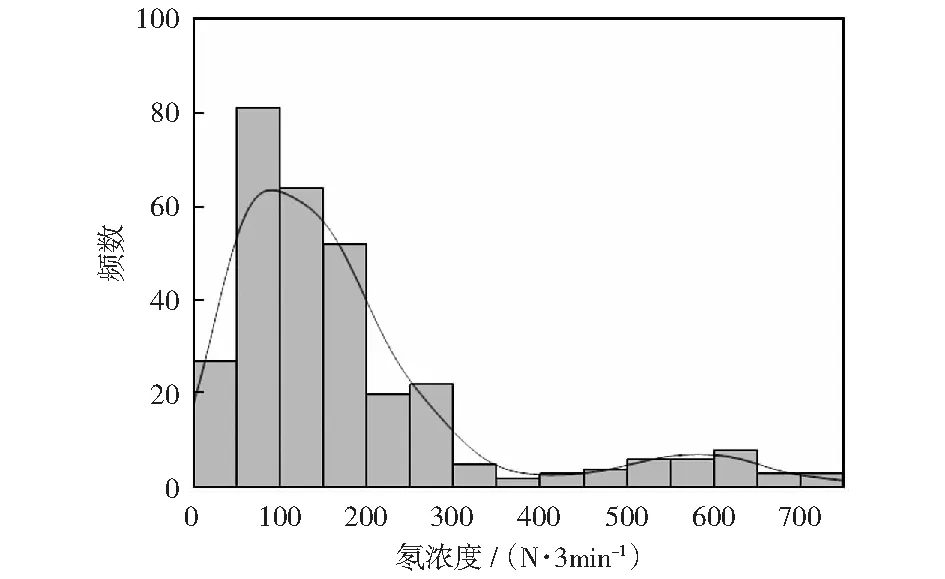
图5 氡浓度计数直方图Fig.5 Radon counts histogram

表1 氡浓度分布统计指标Table 1 Statistical indicators for radon counts

中位数138 N/3 min向左偏离平均数182 N/3 min，频数自左至右逐渐减少，峰度为2.733，偏度为1.807，数据分布呈现不对称状态。

同时，Shapiro-Wilk检验得到P<0.001，在5%的显著性水平下拒绝原假设H0(H0：该随机变量服从正态分布)，即不服从正态分布，因而无法满足插值要求。

所有理论分布中，拟合度最高的是对数正态分布，决定系数R2为0.967 8.同时Anderson-Darling检验得到P值为0.404，在5%的显著性水平下并未拒绝原假设H0(该随机变量服从对数正态分布)，故该矿所测得氡浓度呈对数正态分布，需要经过对数转换才可进行普通克里金插值。

2.4 变异函数建模

对经对数转换后的氡浓度数据进行变异函数建模，球状模型因其决定系数R2为0.78，成为理论模型中对实验变异函数拟合度最优的模型，如图6所示。表2为球状模型变异函数曲线特征值。

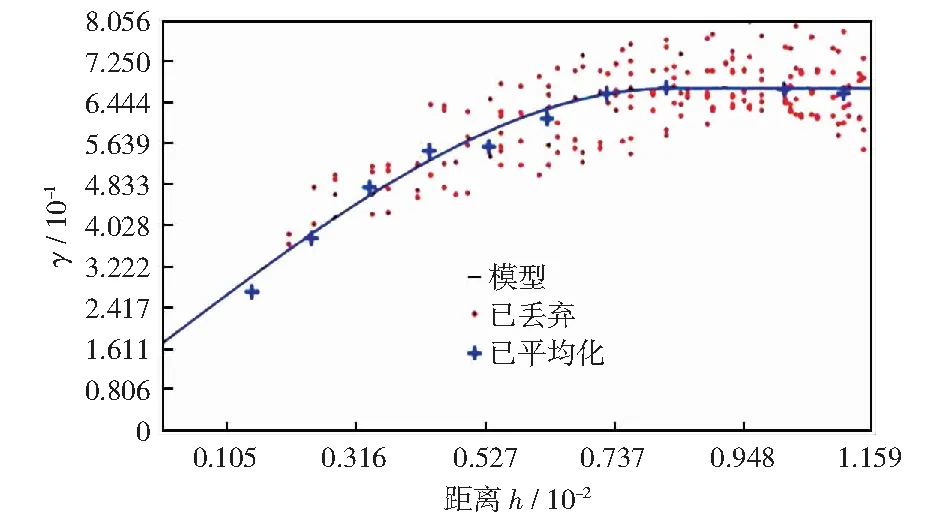
图6 变异函数模型Fig.6 Variogram function model

表2 球状模型变异函数特征值Table 2 Variogram feature values of spherical models

根据普通克里金估计的无偏和方差最小条件，可求出普通克里金方程组的加权系数[19]，进而得到普通克里金的估计值，即测场每一个数据点的氡浓度计算值(见图7).

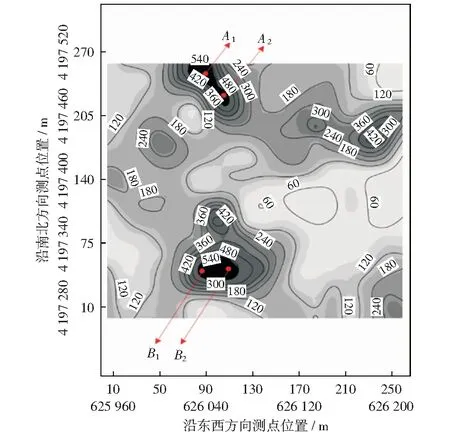
图7 普通克里金插值分布Fig.7 Ordinary Kriging interpolation distribution

3 结果及讨论

将测场区域内西南角第一个测点作为坐标(0,0)点，以测场东西方向的边界连线作为x轴，以南北方向连线作为y轴，构建测场坐标系，如图7、图8中内圈数据所示。两图中外圈数据代表通用横墨卡托投影坐标(universal transverse mercartor，UTM)，是由各测点经纬度坐标经投影变换所形成(通过GPS定位的测点经纬度坐标属于地理坐标系统，无法构建平面插值分布图，需转换为投影坐标系)。

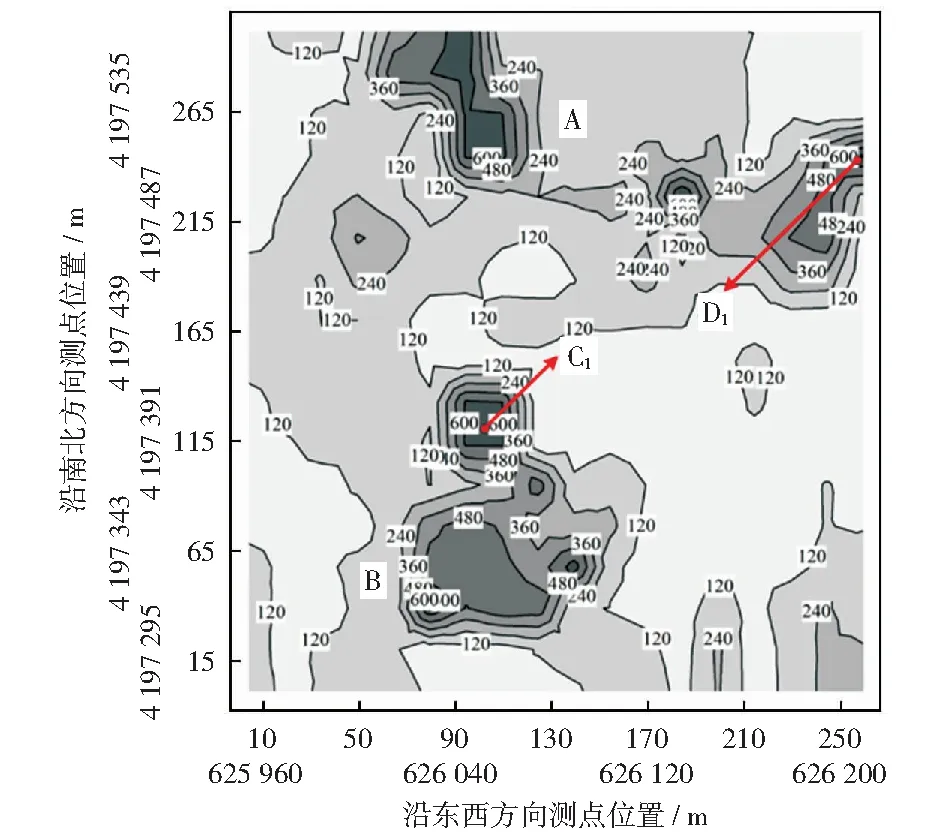
图8 最小曲率插值分布Fig.8 Minimum curvature interpolation distribution

3.1 普通克里金插值分析

结合图4中箱形图分析所给出的异常值范围(487 N/3 min～743 N/3 min)，在图7所示区域内圈定氡浓度异常区域2处：区域A形状近似椭圆状，呈西北-东南走向，面积约800 m2，域内氡浓度极值点有2处，坐标分别为A1(86，247)、A2(106，228)，氡计数为685 N/3 min、637 N/3 min.区域B呈东西走向，面积约850 m2，氡浓度极值点有2处，坐标B1(83，42)、B2(112，46)，组成“双峰”向四周逐渐递减，氡计数分别为743 N/3 min、658 N/3 min.以上4点均呈现由中心极值向四周均匀递减趋势，基本符合煤自燃演化规律，可以确定为疑似着火点。需要特别说明的是，从4处疑似火源点的横纵坐标可以看出其并不局限于测点坐标，这是因为通过插值在测点之间形成了若干数据点，均可作为火源点的位置。

3.2 最小曲率法插值结果分析

同样结合箱形图分析所给出的异常值范围，在图8所示最小曲率法插值分布图中圈定4处疑似着火区域，较之普通克里金插值结果增加C、D两处。区域C形状近似圆形，面积约450 m2，域内极值点1处，坐标为C1(108,118)，氡计数为624 N/3 min.区域D呈东北-西南走向，面积约700 m2，域内极值点1处，坐标为D1(258,247)，氡计数为547 N/3 min，可确定C1、D1为疑似着火点。

3.3 钻孔验证

分别对以上疑似着火点位置进行钻孔测温验证，并对孔底CO浓度进行测定，最终结果如表3所示。

表3 孔底数据表Table 3 Hole bottom data sheet

点A1、A2、B1、B2均超过了煤炭自燃的临界温度(60 ℃～85 ℃)且存在CO气体，并且在钻探过程中点A1、B1、B2孔口有剧烈的热气冒出，所取煤心有明显燃烧过的特征；点A2在钻探过程中孔口冒热气，所取煤心有烘烤现象，表明以上疑似着火点确定存在不同程度的煤自燃现象。点C1孔底温度介于自燃临界温度之间，钻探过程中孔口有少量热气冒出，所取煤心无燃烧或烘烤迹象，说明该点尚处于自热阶段。点D1孔底温度较低，煤层无烘烤现象，顶板砂岩新鲜，且无CO气体存在，可以认为该钻孔区域未发生煤炭自燃。

综上所述，根据普通克里金法插值形成的氡浓度分布所圈定的火源位置，排除了最小曲率法所圈定的疑似着火点C1、D1，准确度更高。

4 结论

1) 反应氡浓度变异函数的数球状模型特征值中，块金值与基台值的比值较小(0.340 7)，介于0.25～0.75之间，说明土壤氡这种变量具有中等的空间相关性，即一定范围内的相邻测点之间能够相互影响，也从侧面证明了使用地统计学中克里金插值方法的必要性。

2) 使用普通克里金插值方法能够将最小曲率法圈定的4处疑似火区(A、B、C、D)缩小为2处(A、B)，将疑似高温火源点由6个(A1、A2、B1、B2、C1、D1)减小到4个(A1、A2、B1、B2)，钻孔验证的高温火源点位置与普通克里金插值方法所圈定的结果一致，说明使用普通克里金插值法在针对土壤氡浓度的区域化变量的分析中具有一定的优越性，能够避免最小曲率法造成的插值失真，可提高同位素测氡法对火源位置判断的准确度，对煤自燃火灾的防治具有指导作用。