横观各向同性土中大直径桩的纵向振动分析
2022-07-28杨冬英冯玮杰李学东
杨冬英, 冯玮杰, 李学东
(1.苏州科技大学土木工程学院, 苏州 215011; 2.江苏苏州地质工程勘察院, 苏州 215011)
近年来桩土相互作用的动力问题作为岩土工程和地震工程的热点问题被学者们广泛研究,其研究成果也被广泛运用到工程实际中。其中,针对工程实践中大量应用的大直径桩,其振动机理研究也在持续中。目前,传统的一维杆件理论已不再适用,Love在Rayleigh考虑杆件的横向惯性效应基础上得到了修正后的杆件运动方程[1],此方程被运用到大直径桩的研究上。龚志超等[2]、Li等[3]、Liang等[4]、何伟杰等[5]、何梦泽等6]基于Rayleigh-Love杆模型分别对均质、非均质土中大直径桩的纵向振动规律进行了研究。李强等[7]、吕述晖等[8]、李曼等[9]考虑土体的三维波动效应,给出了大直径桩纵向振动的理论解。
以上对于大直径桩的动力特性研究都是将桩周土视为各向同性介质。然而,在实际工程中,土颗粒在沉积的过程中其横向及纵向性质往往产生差异,横观各向同性更加符合这种规律[10]。郭楠等[11]利用试验对横观各向同性土与各向同性土进行对比分析得到了二者力学特性不尽相同的结论。因此,研究横观各向同性土中桩的振动规律更加具有实际意义。目前,学者们在此方面已经取得了一些成果。Chen等[12]忽略土体应力沿深度变化,求解了横观各向同性土中弹性桩的扭转振动响应解。张智卿等[13]、郑长杰等[14]考虑土体应力沿深度变化分别对实心桩、管桩在横观各向同性土中的扭转振动规律进行了研究。高洪波[15]在桩底固定边界的条件下研究了单桩在饱和横观各向同性土纵向振动的动力响应解。吴文兵[16]基于虚土桩法给出了单桩在横观各向同性土中的纵向振动响应解。但是,到目前为止,将横观各向同性土与大直径桩结合进行的振动规律研究还相对不足。考虑到大直径桩在工程实际中的广泛使用以及土体的实际情况,研究大直径桩在横观各向同性土中的振动规律就显得十分必要。
现视土体为横观各向同性土,考虑横向惯性力,进行大直径桩的纵向振动特性研究,并对理论研究解析解的准确性展开对比分析。
1 计算模型与基本假定
横观各向同性土-大直径桩的计算模型为三维轴对称模型如图1所示。z为纵向坐标轴,r为径向坐标轴。其中,土体密度为ρ,土体底部为黏弹性支承,并简化为Kelvin线性分布式,其分布式弹性系数和阻尼系数分别为ks、cs。桩长为H,桩径为r0,密度为ρp,弹性模量为Ep,桩顶受到F0eiωt的简谐激振力,桩侧壁受到来自土体的摩擦力,表示为fs,桩底采用黏弹性支承,弹性系数和阻尼系数分别用kb、cb表示。

z为纵向坐标轴;r为径向坐标轴;H为桩长;r0为桩径;ks、cs分别为分布式弹性系数和阻尼系数;fs为桩侧壁受到来自土体的摩擦力;kb、cb分别为弹性系数和阻尼系数;F(t)=F0eiωt为桩顶受到的简谐激振力图1 桩-土动力系统力学模型Fig.1 Mechanical model of pile-soil dynamic system
基本假定如下。
(1)桩周土为横观各向同性黏弹性土,土体材料阻尼采用黏性阻尼形式,其大小与应变率成正比。
(2)土体顶部为自由表面且正应力为0,底部为黏弹性支承。
(3)忽略土体径向、切向位移,只考虑土体纵向位移。
(4)桩身为均质黏弹性材料,桩底为黏弹性支承。
(5)桩土变形为小变形且桩土接触面上应力、位移连续。
2 横观各向同性土体运动方程
2.1 方程的建立
在三维轴对称条件下,根据丁皓江[17]对横观各向同性材料本构方程的描述,忽略土体径向、切向位移,建立土体运动方程为

(1)
式(1)中:uz(r,z,t)=Uz(r,z)eiωt为土体纵向位移,Uz(r,z)为土体纵向位移幅值;ω为振动圆频率;

分别为各方向泊松比;ηs为土体黏性阻尼系数。
对式(1)进行整理,考虑土体谐和振动,将uz(r,z,t)=Uz(r,z)eiωt代入式(1)得

(2)
2.2 边界条件
土体上部自由表面正应力为0,即
σz|z=0=0
(3)
土体底部为黏弹性支撑,即

(4)
无穷远处土体位移趋于0,即
uz|r→∞=0
(5)
2.3 方程的求解
采用分离变量法,令Uz=R(r)Z(z),代入式(2),得

(7)
解方程组式(6)、式(7),得
Z(z)=Csin(hz)+Dcos(hz)
(8)
R(r)=AK0(qr)+BI0(qr)
(9)
式(9)中:I0(qr)、K0(qr)分别为第一类、第二类零阶修正贝塞尔函数;A、B、C、D均为待定常数。
根据边界条件[式(5)],得B=0;根据边界条件[式(3)],得C=0;根据边界条件[式(4)],得

(10)
由式(8)~式(10)可得土体纵向位移解为

(11)
桩周土对桩侧壁的纵向剪应力幅值可表示为

(12)
为了计算方便,引入下列无量纲:
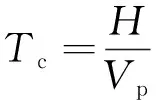
3 大直径桩的纵向振动方程
3.1 方程的建立
根据Rayleigh-Love杆理论,建立黏弹性大直径桩的纵向振动方程为

(13)
式(13)中:wp(z,t)=Wp(z)eiωt为桩的纵向位移,Wp(z)为桩纵向位移幅值;Ap、ηp、υp分别为桩身截面积、阻尼系数、泊松比;fs=2πr0τrzeiωt为桩侧摩阻力。
对式(13)进行整理,考虑桩身谐和振动,将wp(z,t)=Wp(z)eiωt代入式(13)得

(14)
3.2 边界条件
桩顶受到外力作用为
=-F(t)
(15)
桩底为黏弹性支撑,即

(16)
桩土接触面处位移连续,即
uz|r=r0=wp
(17)
3.3 方程的求解
解方程[式(14)],得
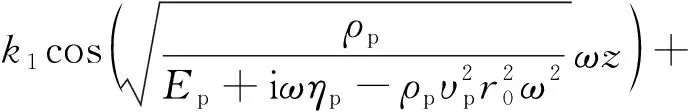

(18)
式(18)中:


(19)
将式(11)、式(18)代入连续条件[式(17)],得
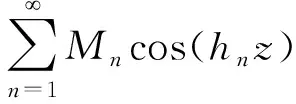
(20)
利用三角函数系的正交性,式(20)两边同时乘以cos(hnz),得
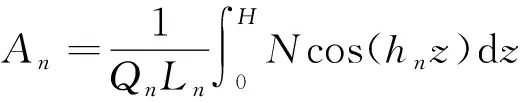
(21)
式(21)中:
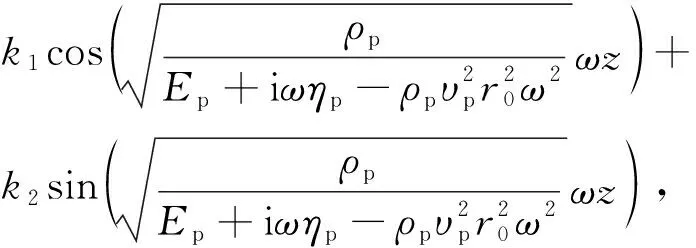


为方便计算,引入以下无量纲变量:
则
根据式(18)、式(19)、式(21),得
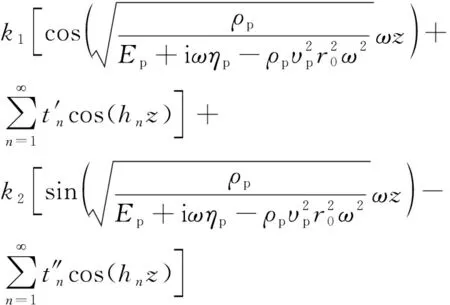
(22)
式(22)中:
将式(22)代入边界条件[式(15)]、[式(16)]得

(23)

(24)
式(24)中:
因此,桩顶复刚度及无量纲化可表示为

(25)
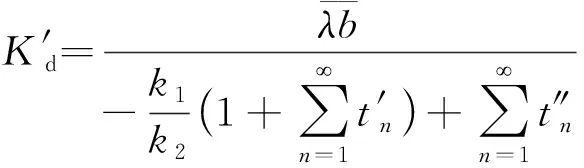
(26)
桩顶速度导纳无量纲可以表示为

(27)
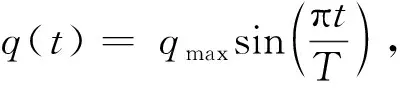
V(t)=IFT[Hv(ω)q(ω)]
(28)
式(28)中:IFT表示Fourier逆变换。对式(28)无量纲化可以得到速度时域响应无量纲表达式为

(29)
4 参数分析
4.1 土体动力响应分析
根据式(11)、式(12)、式(21)可以得到桩土接触面处土体剪切复刚度为
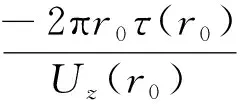

(30)
KK=2πc33KK′
(31)
式中:

定义剪切复刚度无量纲化实部为KK′r,表示土层刚度即抵抗变形的能力;虚部为KK′i,表示土层阻尼即反映能量的耗散。从式(30)可以看出,土体剪切复刚度大小一方面由土体自身参数决定,如横观各向同性参数δ,另一方面取决于桩身参数,如桩径r0,这也体现了桩土振动过程中的耦合作用。


图2 不同横观各向同性参数情况下土体剪切复刚度随频率、深度变化图Fig.2 Variation diagram of complex shear stiffness of soil with frequency and depth under different transversely isotropic parameters
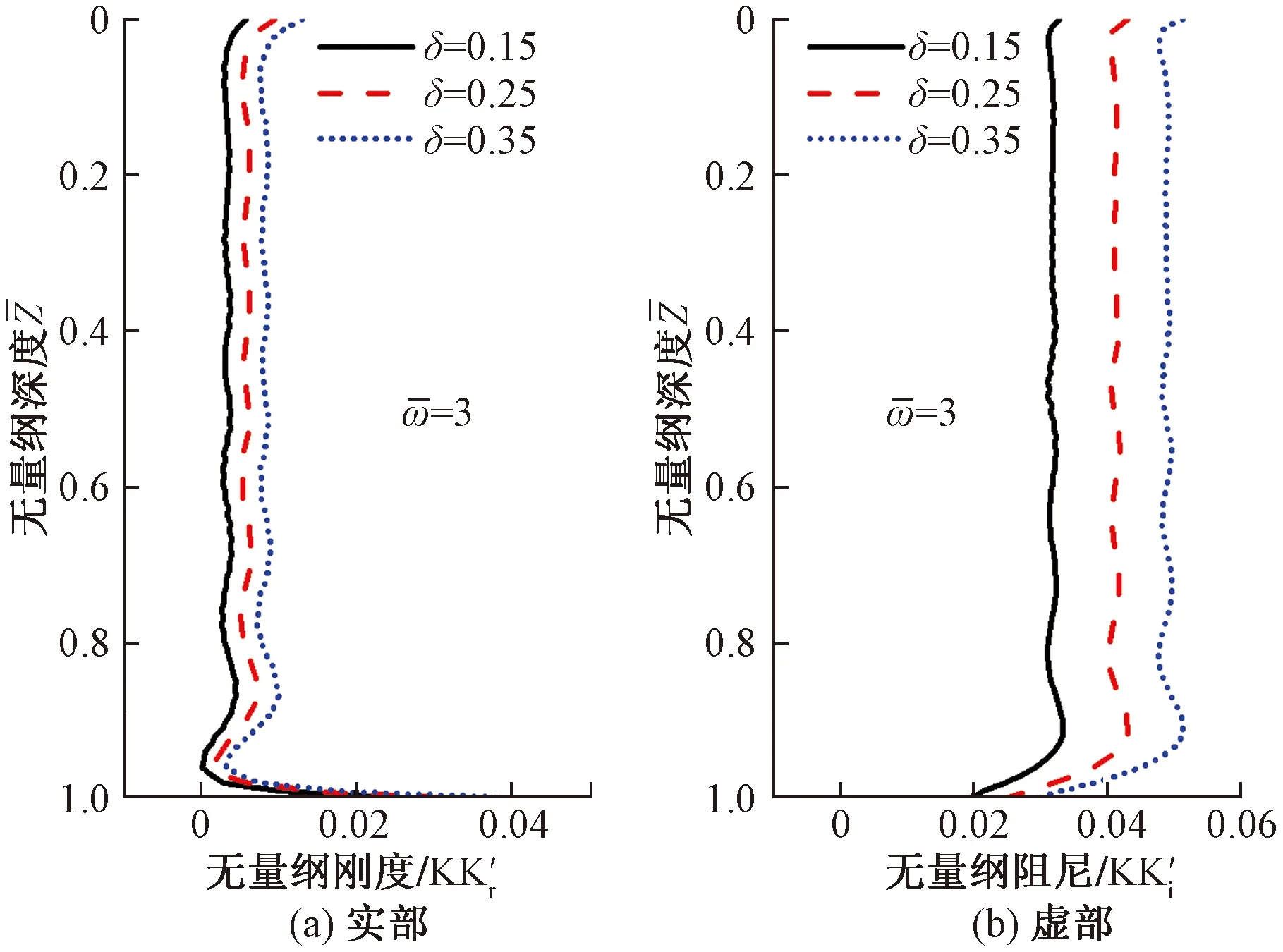
图3 不同横观各向同性参数情况下土体剪切复刚度随深度变化图Fig.3 Variation diagram of complex shear stiffness of soil with depth under different transversely isotropic parameters

图5给出了不同桩径r0情况下土体剪切复刚度随频率、深度变化三维图。从图5(a)、图5(b)中可以看出,桩顶处土体剪切复刚度实部和虚部幅值均随着频率增大而增大,而随着深度的变化,频率影响同样变小。
从图6可以看出,土体剪切复刚度实部受到r0变化的影响仅发生在土体顶部和底部,而在土体中部区域,r0变化产生的影响可忽略不计,虚部阻尼随着r0增大而增大,但增大幅度较小。

图4 不同频率情况下土体剪切复刚度随深度变化图Fig.4 Variation diagram of complex shear stiffness of soil with depth under different frequencies

图5 不同桩径情况下土体剪切复刚度随频率、深度变化图Fig.5 Variation diagram of complex shear stiffness of soil with frequency and depth under different pile diameters

图6 不同桩径情况下土体剪切复刚度随深度变化图Fig.6 Variation diagram of complex shear stiffness of soil with depth under different frequencies
由此可以看出,土体剪切复刚度大小主要由土体自身参数和外部荷载频率决定,桩身参数对刚度影响较小,但对于阻尼影响不可忽略。
4.2 桩顶动力响应分析
4.2.1 土体横观各向同性参数变化的影响

图7 横观各向同性参数对桩顶速度幅频和时域曲线的影响Fig.7 Influence of transversely isotropic parameters on pile top velocity amplitude frequency and time domain curve

4.2.2 桩径变化及横向惯性效应的影响

图8 桩径变化及横向惯性效应对桩顶速度幅频和时域曲线的影响Fig.8 Influence of pile diameter variation and lateral inertia effect on pile top velocity amplitude frequency and time domain curve
图8给出了不同桩径r0及有无考虑横向惯性力情况下桩顶速度幅频和时域曲线。从图8(a)可以看出,随着r0的增大,桩顶速度幅频共振峰值大幅增大,考虑横向惯性效应(υp=0.25)时,共振频率在高频段减小,在低频段基本不变。从图8(b)可以看出,随着r0的增大,反射信号强度增大且考虑横向惯性力时反射信号位置向右偏移。另外,可以发现,桩径越大,横向惯性力的影响越明显。这表明,横向惯性效应是影响大直径桩振动的一个重要因素。
4.2.3 土体黏性阻尼系数变化的影响
图9给出了土体黏性阻尼系数ηs变化对桩顶速度幅频和时域曲线的影响。相比于滞回阻尼对振动较小的影响,考虑的土体黏性阻尼对桩的振动影响很大且更加符合实际情况。从图9(a)中可以看出,随着ηs的增大,桩顶速度幅频共振峰值呈现明显衰减趋势,且共振峰明显变宽。可以看到,当ηs=5×105N·s/m2时,桩顶速度幅频曲线在高频段衰减成一条直线。从图9(b)可以看出,ηs的增大也使得反射信号强度大幅度减小,且在ηs=5×105N·s/m2时反射信号很弱,另外,反射信号宽度也明显变宽。

图9 土体黏性阻尼系数对桩顶速度幅频和时域曲线的影响Fig.9 Influence of soil viscous damping coefficient on pile top velocity amplitude frequency and time domain curve
5 解的验证
5.1 理论解退化
根据王敏中[18]对横观各向同性材料的研究,当弹性常数c44=G,c33=λ+2G(λ、G为第一、第二拉梅常数)时即可退化为各向同性材料。现与胡昌斌等[19]解对比分析,取土体泊松比υ=0.4,即当横观各向同性参数δ=0.167时退化为各向同性材料,再令υp=0即不考虑横向惯性力可退化为胡昌斌解,其余参数取值与胡昌斌解中一致,具体如下:
图10给出了退化为各向同性土时不同波速比条件下桩顶速度幅频和时域曲线与胡昌斌解的对比,发现结果吻合较好,验证了本文理论解的正确性。
5.2 有限元数值模拟
现对圆形截面桩和横观各向同性土相互振动进行有限元数值模拟,采用的单元类型为SOLID185实体单元,考虑到理论解中的轴对称条件,建模采用1/4桩土模型,桩长20 m,桩径1 m,桩侧土半径取24 m,高度取为桩长,桩、土底部黏弹性支承建模采用COMBIN14单元模拟,建模如图11所示。桩身参数取值如表1所示, 横观各向同性土参数如表2所示,将桩土参数分配到对应的模型中。
网格划分采用ANSYS软件中的MESHTOOL工具,由于桩模型为主要研究对象且尺寸相对较小,网格划分时采用边长为0.5 m的网格,桩侧土尺寸较大,网格划分时采用边长为2 m的网格,所有网格划分方式均为自由划分,在桩土接触面处土体网格加密,保证了计算的精度,划分结果如图12所示。桩土1/4截面处施加对称约束,土体外边界和黏弹性支承底部施加固定约束,桩土接触面处使用GLUE命令黏接,桩顶处施加半正弦脉冲荷载,求解完成后可以在后处理中得到桩顶速度时域曲线。
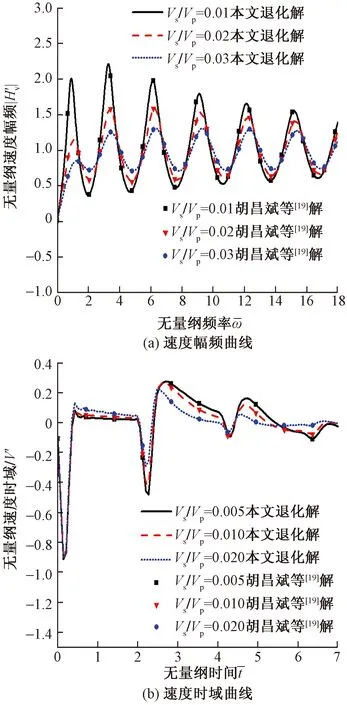
图10 不同波速比情况下本文解与胡昌斌解对比Fig.10 Comparison between the solution of this paper and Hu Changbin’s solution under different wave velocity ratios

图11 模型示意图Fig.11 Schematic diagram of model
图13所示为不同横观各向同性参数δ情况下理论计算解与有限元数值解的对比。可以看出,本文理论解吻合情况较好。另外,随着δ的增大,反射信号峰值减小,这与理论解中δ变化的影响一致,相互验证了本文理论解与数值解的正确性。

表1 桩参数取值Table 1 Values of pile parameters

图12 网格划分示意图Fig.12 Schematic diagram of grid division

图13 不同横观各向同性参数情况下理论解与数值解对比Fig.13 Comparison of theoretical and numerical solutions under different transversely isotropic parameters

表2 横观各向同性土参数取值Table 2 Parameters of transversely isotropic soil
6 结论
考虑土体颗粒沉积过程中各向性质的差异,视土体为横观各向同性黏弹性材料,研究大直径桩在其中的纵向振动规律,得到以下几点结论。
(1)横观各向同性参数的增大导致土体剪切复刚度增大进而对桩顶速度幅频和时域曲线影响显著。具体表现为随着横观各向同性参数的增大,共振峰值减小,反射信号强度降低。
(2)桩径变化对土体剪切复刚度影响较小,但对桩顶动力响应有明显影响,具体表现为桩径增大会显著增大桩顶速度幅频曲线的共振峰值和时域曲线的反射信号强度,并且桩径越大,横向惯性效应的影响越明显。
(3)土体黏性阻尼系数的变化对桩的纵向振动影响明显,具体表现为阻尼系数增大会减小桩顶速度幅频曲线的共振峰值和共振频率,也会降低速度时域曲线反射信号的强度,使反射信号峰值变宽。
(4)各向同性土中不考虑桩的横向惯性力时,本文解能退化为胡昌斌解;本文解与数值计算的对比发现,两种计算结果较吻合,验证了本文理论解的正确性。
