评估零效应的三种统计方法

许岳培 陆春雷 王 珺 宋琼雅 贾彬彬 胡传鹏

（1.中国科学院行为科学重点实验室（中国科学院心理研究所），北京 100101；2.中国科学院大学心理学系，北京 100049；3.浙江师范大学心理与脑科学研究院，金华 321004；4.中山大学心理学系，广州 510006；5.上海体育学院心理学院，上海 200438；6.南京师范大学心理学院，南京 210024）

1 引 言

原假设显著性检验（Null hypothesis significance test，NHST，也翻译为零假设显著性检验或者虚无假设显著性检验）是目前使用最为广泛的统计推断方法。在NHST框架下，研究者通常在假定原假设（null hypothesis，H）为真的前提下，根据p 值是否小于预先设定的α（如：α=0.05）来决定是否拒绝原假设（Wasserstein&Lazar，2016）。若基于当前数据计算得出的p 值小于预先设定的α，则认为当原假设为真时，在一次抽样中出现当前结果（及更极端结果）的可能性非常小，那么研究者就有理由拒绝该原假设。由于NHST 的理论前提是假定原假设为真，这就意味着，p 值大于α 的结果（即统计意义上不显著的结果）并不能作为支持原假设的证据（Greenland et al.，2016；Wasserstein&Lazar，2016）。因此，当研究者将零效应（nil effect，“效应量为零”或者“效应不存在”）作为原假设（这样的原假设又称零假设，nil hypothesis） 时，无法通过NHST 和p 值来评估零效应。

实际研究中，研究者经常需要评估零效应（Linde，Tendeiro，Selker，Wagenmakers，&Ravenzwaaij，2020）。例如，研究者欲证实某干预方法的非劣性，即欲证实新兴的、更为经济的治疗方案相对于常规治疗方案同样有效。又如，在一些实验组/控制组匹配的研究设计中，研究者需要对无关变量进行匹配（如：两组被试的性别、年龄），即希望通过统计推断得到“两组被试来自同一总体”的结论。此外，许多理论会预测在某些情况下某效应不存在，此时证实该特定情况下的零效应可为这些理论提供支持。

另一类常见的情况是，研究者发现基于收集到的数据未能拒绝欲推翻的原假设（即意外的p>0.05 的结果），或是在进行探索性研究（未有明确的研究假设）时发现p>0.05 的结果。此时，研究者要进一步区分是“证据不足”（null of evidence，即由于统计效力低下等其他原因未能探测到本应存在的效应）还是“效应不存在”（evidence of null，即现有数据已经能够为效应大小为零提供了足够证据），同样需要合理评估支持零效应的证据强度（Harms & Lakens，2018）。

NHST 无法评估零效应的局限导致其无法满足实际研究的需要，而能够有效评估零效应的统计方法在心理学研究中仍鲜有提及（温忠麟，方杰，沈嘉琦，谭倚天，李定欣，马益铭，2021）。这就使得研究者在面对p>0.05 的结果时，往往只是将不显著结果进行简单的报告，而无法运用合理的统计方法进行统计推断。Aczel 等人（2018）的研究发现在国际知名心理学期刊上发表的137 篇提及不显著结果的文章中，仅有10.2%的文章利用贝叶斯分析对不显著结果进行了统计推断；而王珺等（2021）分析了2017 和2018 年发表在中国心理学核心期刊上的500 篇文献后，发现其中有180篇在摘要中提及了不显著结果，但无一运用了除NHST 之外的方法对不显著结果进行解读或推断。这一定程度上表明，大部分国内研究者较少了解能够支持零假设的方法（王珺等，2021）。而忽视对不显著结果的进一步分析或错误地认为所有的不显著结果都没有发表价值，会进一步加深发表偏见（胡传鹏，王非，过继成思，宋梦迪，隋洁，彭 凯 平，2016；Forstmeier，Wagenmakers，&Parker，2017）。

对评估零假设的统计方法缺乏了解还间接导致研究者错误地解读不显著结果。许多研究表明心理学专业学生或心理学领域的研究者将p 值误解为原假设为真的概率，错误地将NHST 中不显著结果作为“支持零效应”的证据（Amrhein，Greenland，&McShane，2019；Gigerenzer，2004，2018；Greenland et al.，2016；X. Lyu，Xu，Zhao，Zuo，& Hu，2020；Z. Lyu，Peng，& Hu，2018）。例如：吕小康等的调查发现有超过半数（54%）的相关专业（包括心理学）学生或研究者将“p>0.05”错误解读为“证实了原假设”（X.Lyu，et al.，2020）；在提及不显著结果的已发表的心理学论文中，研究者也易将“p>0.05”的结果作为“支持零效应”的证据，将其解读为“没有差异或效应”（Aczel et al.，2018；王珺等，2021）。

对不显著结果的错误解读可能会直接导致统计推断出现偏差。例如：若研究者进行了一次单因素两水平的被试间实验，欲证一种新疗法的干预效果能够比肩传统疗法，即欲接受两种疗法在某指标上治疗效果相同的原假设。通常的做法是，对因变量进行独立样本t 检验，但仅凭统计检验不显著（如p>0.05）或两组因变量差异的效应量较小（如Cohen’s d<0.30），并不能得到两种疗法无差异（或等价）的结论。此时如果武断地给出两种疗法一样好或等价的结论，则可能直接导致对研究结论的错误推断。利用贝叶斯因子重新分析发表文章中不显著结果的数据，结果表明：绝大部分不显著结果无法为“证实了原假设”这一结论提供较强证据（Aczel et al.，2018；王珺等，2021）。

为弥补NHST 无法评估零效应的局限、帮助更多研究者从不显著结果中获取有效信息，本文结合两个实例来介绍、对比三种可用于评估零效应的统计方法——等价检验（Equivalence test）（Meyners，2012；Rogers，Howard，& Vessey，1993）、贝叶斯估计（Bayesian estimation）（Kruschke，2011；McElreath，2020）和贝叶斯因子（Bayes factor）（Aczel et al.，2018；胡传鹏，孔祥祯，Wagenmakers，Ly，彭凯平，2018）。

2 等价检验、贝叶斯估计和贝叶斯因子的原理

评估零效应的思路主要有两种。一种思路是设定一个足够小的，几乎可以认为效应为零的区间，用于评估零效应（Meyners，2012；Rogers et al.，1993）。这一区间即为“最小感兴趣的效应量区间”，简称为“最小感兴趣区”（smallest effect size of interest，SESOI）。目标效应量在SESOI 内时，研究者可以认为效应量几乎为零，可以忽略不计。采用这种思路进行统计推断的方法有两种，分别是频率统计框架下的等价检验和贝叶斯统计框架下的贝叶斯估计。另一种思路，如贝叶斯因子，通过对比效应量为零的原假设为真时与效应量不为零的备择假设为真时，当前数据出现的可能性，即特定先验分布下不同模型的边缘似然性之比，从而推断当前数据更支持哪个假设。

2.1 等价检验

等价检验从NHST 扩展而来，目的是评估当前效应量是否足够小。等价检验的逻辑来源于最小效应量检验（Minimal-effects test）（Murphy，Myors，&Wolach，2014）。当研究者将零效应作为原假设时（即，原假设为“没有效应”的零假设时），NHST 是将效应量与零做比较，判断在假定效应为零（H）的情况下出现当前数据或者更极端数据的概率是否足够小，从而推断是否拒绝原假设（图1A）。如果研究者将H设定为一个区间，比如[-0.1，0.1]，拒绝原假设则要求基于样本得到的效应量要么在统计学意义上显著大于0.1，要么在统计学意义上显著小于-0.1（图1B），需要进行两次单侧检验。这种做法被称为最小效应量检验。

等价检验则正好将最小效应量检验的H与H所对应的效应区间对调，H在区间之内，而H在区间之外（Lakens，McLatchie，Isager，Scheel，&Dienes，2018；Lakens，Scheel，&Isager，2018）。如果SESOI为[-0.1，0.1]，等价检验的原假设是效应量要么大于0.1，要么小于-0.1 的区间（图1C），即“存在有意义的效应”；其备择假设是效应量在[-0.1，0.1]之间，即效应量太小而可以认为“不存在有意义的效应”。如果当前数据拒绝了原假设，则可以接受备择假设，即“不存在有意义的效应”。

图1 等价检验和贝叶斯估计的原理示意图

等价检验中的原假设和备择假设除了与传统NHST 的原假设和备择假设具有不同的意义之外，其对于原假设的设定要求更高。相对于NHST 中原假设假定效应量为零，在等价检验中，研究者需要指明原假设的范围，即备择假设（SESOI）之外的区间。结合已有研究和实际情况，SESOI 的设定有特定的方式（详见补充材料：osf.io/6mzr9），且必须有合理的原因。

实际检验过程中，等价检验需要将实际数据与SESOI 的下限ΔL 和上限ΔU 分别进行单侧的显著性检验，即两次单侧检验（Two one-side tests，TOST）。一次单侧检验的原假设是当前数据的效应量小于SESOI 的下限ΔL；另一次单侧检验的原假设则是当前数据的效应量大于SESOI 的上限ΔU。最后结合两个单侧检验的统计结果进行等价检验的推断：当且仅当TOST 中的两个p 值均小于α 水平时，依据NHST框架的逻辑拒绝原假设，可以接受备择假设（“不存在有意义的效应”）。此时研究者可以认为存在统计上的等价性结果，即此效应足够小，在这一研究群体中是可以忽略的。但只要TOST 中有一个p 值大于α水平，就无法拒绝原假设（“存在有意义的效应”），即统计结果不能支持等价的结论（Lakens，Scheel，&Isager，2018）。

值得注意的是，等价检验也可以通过基于参数估计的方法实现。频率统计框架下，研究者可以估计效应的值及其置信区间（王珺等，2019），然后根据效应量置信区间与SESOI 重合的比例进行推断（Tryon，2001）。例如，当研究者把α 水平设为0.05时，可以对当前数据的效应量进行参数估计计算得到其（1-2α）%（即90%）的置信区间（由于需独立进行两次α 水平为0.05 的单侧检验，因此等价检验需对效应量构建90%的置信区间，而非95%的，见Linde et al.，2020）。若其效应量90%的置信区间与设定的SESOI 没有重合（即其置信区间的上下限均不超出SESOI 的上下限），这就等同于TOST 中的两个p 值均小于0.05，意味着存在统计上的等价性结果；反之，若其效应量90%的置信区间与设定的SESOI 出现了重合（即其置信区间的上限或/和下限超出了SESOI 的上下限），这就意味着当前结果不能支持存在统计上的等价性结果。

2.2 贝叶斯估计的原理

贝叶斯估计是贝叶斯统计框架下的参数估计方法（Kruschke&Liddell，2018）。贝叶斯统计（bayesian statistics）与频率统计（frequentist statistics）的主要区别在于对概率（probability）的理解。频率统计中的概率表示在无数次的重复抽样中对于频率（frequency）的期望，即长期行为表现的结果。而贝叶斯统计中的概率表示基于已有的信息，发生当前事件的可信程度（credibility） （Kruschke，2014；McElreath，2018）。具体到推断统计中，频率统计认为总体参数为固定值，而贝叶斯统计认为总体参数是对应概率分布下的随机取值，并且概率分布可以随着数据的获取而不断更新。贝叶斯统计的核心是贝叶斯法则（Bayes rules）。如果我们为了估计某一总体分布的参数（θ）而抽取了一定样本或“数据”（data），基于贝叶斯法则可以得到下述公式：

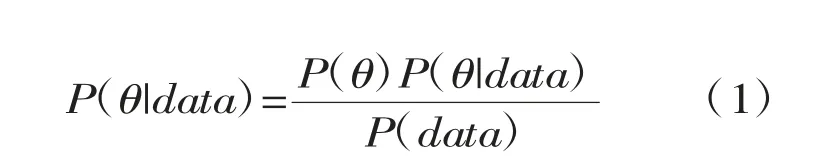
其中，P（θ）表示在获得数据前对于参数取值的信念， 即先验分布（prior distribution）；P（θ|data）表示获得当前数据后对先验分布进行更新后所得到的信念或者概率分布， 即后验分布（posterior distribution），通常是研究者想进行估计的。计算后验分布不仅需要先验信息，还需要P（data|θ）和P（data）。P（θ|data）表示当参数值为θ时，出现当前数据的可能性，即似然性（likelihood），也有文章将其称为某个参数取值的预测充分性（predictive adequacy）（van Doorn et al.，2021）；P（data）表示参数所有可能取值的加权求和或者积分得到的边缘概率或者边缘概率密度，亦可理解为归一化因子（normalizing factor）。简而言之，贝叶斯统计可以随着数据的累积不断更新后验，进而改变对参数不同取值的可信度（Kruschke&Liddell，2018）。

应用贝叶斯估计评估零效应时，通过比较效应为零时的参数取值范围与后验分布下参数概率分布的差异进行统计推断（Kirkwood & Westlake，1981；Rouder，2014；Westlake，1976）。这里后验分布下的参数概率分布使用最高密度区间（highest density interval，HDI）表示，而效应为零时的参数取值范围是研究者预先设定的实际等价区（region of practical equivalence，ROPE）（Kruschke，2014，2018）。ROPE 类似于前文介绍的等价检验中SESOI，是一个包括零的几乎可以忽略的效应区间。确定ROPE 后，可以考察参数后验分布的95%HDI 与ROPE 的重合度来评估零效应。当95%HDI完全落在ROPE 之内时，说明可能性最高的参数实际上等价于0，因此可以接受零效应（图1D）；当95%HDI 和ROPE 部分重合时，意味着只有部分可能性高的参数取值等价于0，此时无法做出明确判断（图1E）；当95%HDI 完全落在ROPE 之外时，说明可能性最高的参数全部都不等价于0，因此可以拒绝零效应（图1F）（Kruschke，2011）。

值得注意的是，贝叶斯估计本身是基于数据进行模型拟合的过程，因此研究者可以使用不同的先验和不同的模型。在这个过程中，需要考虑先验分布设定的合理性以及MCMC 抽样收敛（convergence），具体可以参考Depaoli 和van de Schoot（2017）以及van de Schoot 等（2021）。

2.3 贝叶斯因子的原理

贝叶斯因子的基本思路是通过模型比较的方式，获得不同模型下出现当前数据的可能性的相对比值。它尝试回答的问题是当前数据更可能在哪个模型为真的情况下出现。当用于假设检验时，贝叶斯因子中的模型可参照NHST 中的原假设和备择假设进行设定。例如要评估效应为零的原假设与效应量不为零的备择假设时，可将原假设设定为零模型M（即point null model，θ=0，效应量为0 且无须参数分布），备择假设为M（θ≠0，效应量不为0 且需要通过模型内先验定义其概率分布）。换而言之，上文式（1）中的P（data|θ）中的参数θ实质上是在某种模型下的参数。在进行贝叶斯假设检验时，原假设与备择假设对应的模型参数（θ）的取值分布均会具体化。P（data|θ）在两个假设模型之下分别为：P（data|θ，M）和P（data|θ，M）。而贝叶斯因子就是以这两者的比值定义的（Keysers，Gazzola，&Wagenmakers，2020；Wagenmakers et al.，2018）：

其中，BF的下角标中0 在前，1 在后，表示BF为H相对于H的贝叶斯因子。反之，BF就是将式（2）中的分子分母颠倒，表示H相对于H的贝叶斯因子。BF=9 表示当前数据出现在H为真的情况下的可能性是出现在H为真的情况下的9 倍。可依据贝叶斯因子的大小推断当前数据对两个模型的支持证据的相对强度。关于贝叶斯因子的决策标准，可参考Lee 和Wagenmakers（2013） 基于Jeffreys（1961）提出的结果分类陈述（胡传鹏等，2018）。例如，BF在[3，10]之间时，可以解读为当前数据提供了中等强度的证据（Moderate evidence）来支持原假设（H）。

作为贝叶斯统计推断的一种方法，贝叶斯因子同样涉及先验的选择。一般根据先前研究确定先验，比如使用元分析得到的效应量及其对应的分布作为先验。而对于没有相关元分析的原创性研究，更常见的做法是使用一个标准化的先验，比如在贝叶斯t 检验中，用柯西分布作为备择假设的先验（Rouder，Speckman，Sun，Morey，&Iverson，2009），δ ～Cauchy（χ=0，γ=1）：其中χ 为位置参数（location parameter），定义分布下的峰值位置，与正态分布中的均值类似；γ 为尺度参数（scale parameter），定义分布下包含峰值50%参数取值范围的一半宽度，与正态分布中标准差类似。为了让备择假设的先验更符合心理学研究中效应量分布的真实状况，常用的计算贝叶斯因子的R 包BayesFactor 将默认的先验设定为Cauchy（0，0.707），即以0 为峰值，从-0.707到0.707 包含分布下50%的参数可能取值（Tendeiro and Kiers 2019）。备择假设模型中参数先验分布的选择会对最终计算的BF值有较大影响。以贝叶斯t 检验为例，其他条件相同的前提下，备择假设模型内的先验Cauchy 分布尺度参数γ 越大（分布越离散），贝叶斯因子的计算结果就偏向零模型（BF越大），因此通常情况下需要研究者对贝叶斯因子分析结果进行稳健性分析，即考察不同先验分布下贝叶斯因子的结果获得更为可靠的统计推断。

3 等价检验、贝叶斯估计、贝叶斯因子的应用和比较

以下将展示如何在两个真实的数据中应用上述三种方法。此二例数据均采用NHST 框架下的独立样本t 检验，且p 值未达到显著水平。我们采用等价检验、贝叶斯估计和贝叶斯因子对此二例数据进行重新分析，并从评估零效应的能力、是否用到SESOI/ROPE、是否报告不确定信息和可拓展性方面比较了三种方法。分析使用了R统计软件包4.0.2（R-Core-Team，2019）。其中，等价检验使用的是TOSTER 工具包（Lakens，2017），贝叶斯估计采用BEST 工具包（Kruschke & Meredith，2020），贝叶斯因子采用BayesFactor 工具包（Morey &Rouder，2018）。实例1 展示的是数据无较强证据支持零效应的情况，而实例2 展示的是数据相对较强地支持零效应的情况。分析涉及的所有的数据、代码、结果及其解释见osf.io/54qpv/。

3.1 实例1：Kitchen Rolls

实例1 的数据来自JASP（jasp-stat.org）分析软件的示例数据“Kitchen Rolls”。该数据源自Wagenmakers 等（2015）对Topolinski 和Sparenberg（2012）进行的重复研究。原研究的第二个实验中，两组被试分别以顺时针方向（N=30）和逆时针方向（N=30）拨动卷纸，然后填写一个测量开放性的问卷。结果发现，相比于逆时针拨动的被试，顺时针拨动的被试的开放性得分更高，t（58）=2.21，p<0.031，d=0.58。Wagenmakers 等（2015）在预注册之后，重复了该研究的实验二。研究的数据包含两组被试在开放性人格特质上的得分，其中一组被试在填写问卷前顺时针旋转桌面上的纸卷（N=48），而另一组则在填写问卷前逆时针旋转纸卷（N=54）。

由于等价检验和贝叶斯估计在统计过程中需要用到SESOI 或ROPE，因此首先需要确定SSEOI。本分析参考Simonsohn（2015）提出的重复研究中确定SESOI 边界的方法，将SESOI 的等价边界设置为原研究样本量之下，33%检验力可探测到的效应量，即SESOI 为[-0.40，0.40]（计算过程见在线R Notebook，osf.io/gn2hm/）。

NHST 未发现两组被试在开放性上的得分差异达到统计显著，t（100）=- 0.75，p=0.453，d=-0.149。贝叶斯因子则为零效应提供了中等强度的证据，BF∈（3，10），具体而言，不同先验——Cauchy（0，0.707）、Cauchy（0，1）、Cauchy（0，1.5）——之下的贝叶斯因子分别为BF=3.71、5.02、7.31。等价检验和贝叶斯估计的结果基本一致，即无法判断数据是否支持零效应：在贝叶斯估计中，95%HDI 和ROPE 部分重合；在等价检验中，TOST 左侧的p 值大于α 水平（图2A）。综合三种方法，可认为该数据无法为零效应提供较强的证据，同时也无法为效应的存在提供较强的证据。这提示研究者需要进一步分析实验设计中可能存在的问题，并进行下一步研究和分析。

3.2 实例2：Sociometric status and well-being

实例2 的数据来自Many Labs 2 项目（osf.io/uazdm/）中的一个研究。Many Labs 2由36 个国家和区域的不同实验室合力完成，共重复了28 个经典的实验，总样本量达15305（Klein et al.，2018）。实例2 的数据来自报告中的第12 个重复研究“Sociometric status and well-being”。该研究重复原研究中的实验三，探究相对于社会经济地位，社会关系地位与幸福感的关系是否更紧密（Anderson，Kraus，Galinsky，& Keltner，2012）。原研究中报告了一个显著的简单效应分析结果，相对低社会关系地位条件的被试，高社会关系地位条件的被试有更高的 主 观 幸 福 感，t（115）=3.05，p=0.003，d=0.57，95%CI[0.20，0.93]。Many Labs 2 主要重复了原研究中主观幸福感有差异的低社会关系地位条件和高社会关系地位条件，共包括6905 个样本。同实例1，我们用三种统计方法进行分析。在分析之前，我们同样采用实例1 的方式确定SESOI 和ROPE为[-0.20，0.20]。

NHST 未 发 现 显 著 的 效 应，t（6903）=-1.76，p=0.079，d=-0.04。然而等价检验、贝叶斯估计和贝叶斯因子的统计检验结果均支持了零效应（图2B）。等价检验的结果表明，对SESOI 的下、上限的两次单侧检验均显著（p<0.001）。对于贝叶斯估计，两组差异效应量的95%HDI 完全落在ROPE内。贝 叶 斯 因 子 在Cauchy（0，0.707）、Cauchy（0，1）、Cauchy（0，1.5）三种先验分布下的结果分别为：BF=7.87、11.11、16.64，达到了中等和较强程度支持零效应的证据（Lee&Wagenmakers，2013）。其中，当先验分布的尺度参数变大时，BF趋向于提供较强程度支持零效应的证据。三种评估零效应的方法一致支持了零效应，研究者可以较有信心地推断目标效应为零。

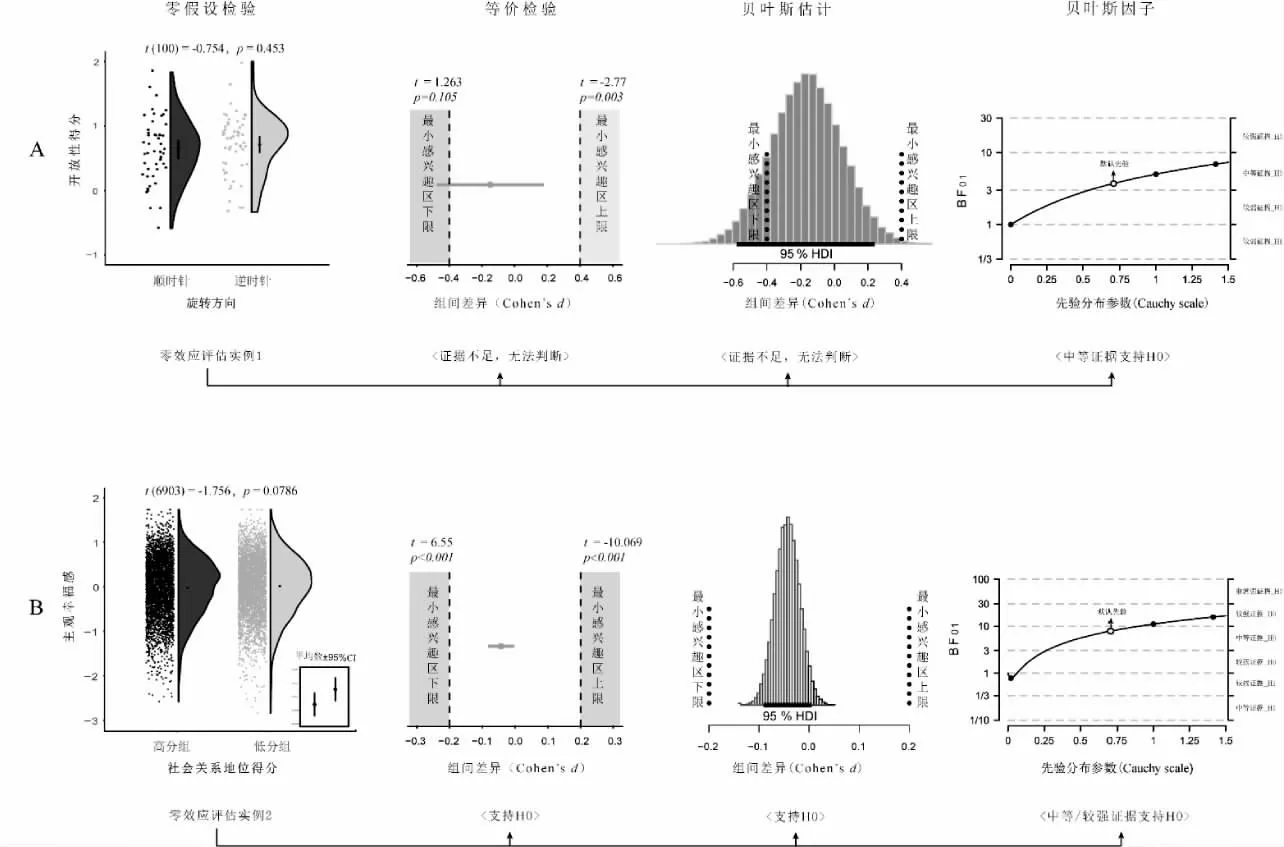
图2 四种统计检验对两个实例数据的分析结果与推论

3.3 等价检验、贝叶斯估计、贝叶斯因子的比较

在NHST 框架下，以上两个实例数据均没有得到p<0.05 的结果，即未能拒绝原假设。然而，这并不意味着当前数据可以支持零效应的存在。实例1 的结果表明，虽然NHST 得到的p 值较大，但等价检验、贝叶斯估计、贝叶斯因子分析均表明该数据并不能为零效应提供较强的证据。而实例2的结果则表明，样本效应量与事先确定的近似于零的区间（SESOI/ROPE）无差别，而贝叶斯因子也提供了较强的支持零效应的证据，因此可以得到零效应的推论。两个实例数据的研究设计相对简单，因此三种方法均可以使用。但在更加复杂的研究设计中，是否能够同时使用三种方法可能需要进行深入地考察。以TOSTER 包为例，等价检验目前只包括了t 检验、元分析、相关分析等方法（Lakens，2017），这意味着其可拓展性方面存在限制。为了帮助研究者采用合适的方法，本文从几个维度对NHST 和三种方法进行比较（表1）。

表1 原假设检验、等价检验、贝叶斯估计和贝叶斯因子的特征及其对比。“O”表示有此特征，“X”表示无此特征。

首先，等价检验、贝叶斯估计和贝叶斯因子均可以用来支持零效应，这是它们区别于NHST 之处。因此，研究者在得到不显著结果时，可以采用这三种方法进一步从不显著结果中提取信息。其次，如果研究者希望支持零效应，使用等价检验与贝叶斯估计均需要使用SESOI（Kruschke & Liddell，2018；Lakens，Scheel，&Isager，2018），这意味着研究者需要提前确定一个合理的区间，才能进行合理的推断。但是计算贝叶斯因子时，则不需要确定SESOI。第三，等价检验和贝叶斯估计提供了关于推断中不确定性的信息，且后者提供的不确定信息更为详实，描绘了参数的不同取值出现的相对概率（Kruschke & Liddell，2018）；而贝叶斯因子本身不提供这些信息。第四，从可拓展性上来看，理论上三种方法均可以广泛适用于各个情境，但不同情境均需要对模型进行设定。从实践上来看，由于众多工具包的出现（如R 语言包brms，Bürkner，2017），贝叶斯估计可以相对简便地运用于线性和一般线性回归模型的（Kruschke &Liddell，2018；Kruschke & Meredith，2020），但是贝叶斯因子和等价检验目前可获得的工具包则仍然较为限制。具体而言，贝叶斯因子目前主要可用于t 检验、相关分析、方差分析和线性回归分析等常用的统计模型（Morey&Rouder，2018）；而等价检验（基于TOSTER）主要可用于t 检验、元分析和相关分析（Lakens，2017）。对于更加复杂的研究设计，如中介、调节分析等，贝叶斯因子和等价检验尚未被整合到便利的工具包中。

除了三种方法原理特征上的差异外，随着样本量、等价区间的变化，三种方法的统计检验力（即效应量真值在等价区间内时，统计结果判断为等价的概率）也有不同。Linde 等研究者（2020）通过一系列的模拟发现贝叶斯因子相对另外两种方法有更强的统计检验力，并且在样本相对较小的时候有更高的辨别力。

类似地，以上述两个实例的具体参数（样本量、等价边界）作为模拟参考，我们的模拟也发现，当效应量真值在区间[0，0.5]时，贝叶斯因子的统计检验力（即真实效应量落在等价区间，统计方法推断可以看作是效应量为零的比例）较高。但同样，其假阳性也更高（即真实效应量不在等价区间，但统计方法的结果认为其效应量可以看作为零的概率）（见图3）。贝叶斯因子较高的敏感性在样本量小的时候更加明显，因此贝叶斯因子可能是小样本研究中用以支持零效应较好的方法，而适当收紧其判断标准（如将BF>10 作为等价标准，而非BF>3）是权衡其较高统计检验力和较高一类错误的有效策略之一。

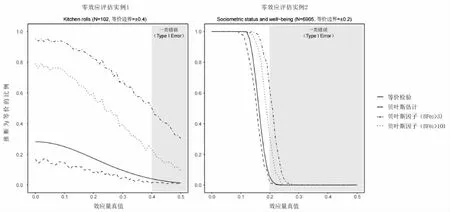
图3 等价检验、贝叶斯估计和贝叶斯因子在不同样本量、等价边界上的统计检验力及一类错误率

三种方法相对于NHST 均可以用于支持零效应，然而结果解释上存在理论上的区别。等价检验通过引入SESOI 弥补了NHST 功能上的缺陷，即不能用于推断效应不存在（Greenland et al.，2016；Wasserstein&Lazar，2016）。其所在的统计框架仍为频率统计，即将统计推断建立在无数次的重复抽样中对于频率（frequency）的期望上。而基于贝叶斯统计框架下的贝叶斯因子和贝叶斯估计则有所区别。贝叶斯因子的统计推断本质上基于模型比较，即比较当前数据在两个相互竞争的模型中出现的相对概率（Keysers et al.，2020；Wagenmakers et al.，2018；胡传鹏等，2018）。贝叶斯估计则通过估计后验分布的95%HDI 与类似于等价检验中SESOI 概念的ROPE 进行比较得到结论。推断的形式上，贝叶斯估计和等价检验相似，然而前者的HDI 与后者的CI 在对概率的认识上存在本质上的区别，也即贝叶斯统计和频率统计之间对概率不同认识 上 的 区 别（Kruschke，2014；McElreath，2020）。

4 总结与建议

心理学研究中不同的统计方法正在相互融合中共同发展，但对于评估零效应的方法却仍然受到相当程度的忽视（温忠麟等，2021）。等价检验、贝叶斯估计和贝叶斯因子等统计方法的出现，一定程度上弥补了传统NHST 无法评估零效应的缺陷，帮助研究者进一步区分“有证据支持零效应”和“没有证据支持有效应”这两种情况。本文介绍的三种方法在多个方面存在差异，各有特点，研究者可以根据当前研究的情况选择合适的方法。例如从便捷性上考虑，使用JASP 软件进行贝叶斯因子分析是一个不错的选择。首先JASP 是一款免费使用的开源统计软件，能够覆盖心理学研究中常用的统计分析方法；其次它依托图形用户界面进行操作，对编程的需求相比其他两种方法更低；最后JASP 的使用手册比较完备，且有相应的分析与结果报告指南（van Doorn et al.，2021），此外，在其网站（jasp-stats.org）与论坛（https：//forum.cogsci.nl/index.php?p=/categories/jasp-bayesfactor）也可以进一步获取必要的指导信息。如果从方法的严谨性上考虑，研究者可以同时采用多种方法评估零效应，便于交叉验证，提高统计推断的可靠性。当然这意味着研究者需要投入相当的精力去获取必要的知识和技能（如形成基本认识，明确使用前提，规范统计报告等），避免统计方法的滥用和误用（Gigerenzer，2018）。此外，当研究设计较为复杂时，缺乏必要的统计背景和编程技能会让一些研究者束手无策或者误用这些方法，因此，研究初期提出清晰的研究假设并据此在实验设计上尽量精简会对后续的数据分析有裨益（一个较详尽的如何选择恰当的方法的流程，可参考补充材料中的流程图）。

最后，我们建议，评估零效应时注意以下三点：其一，如果采用等价检验和贝叶斯估计的方法，需要清楚地报告所采用的SESOI/ROPE，并论证其合理性；如果采用贝叶斯估计或者贝叶斯因子，还需要澄清所采用的先验及其合理性，也可以报告不同先验下的结果稳定性。其二，如果可行，建议同时采用多种分析方法，交叉验证同一个结果的稳定性，例如上文的两个实例分别使用三种方法评估零效应。其三，如有可能，在研究开始前或者数据分析前进行预注册，预注册中可以提供评估零效应的相应方法和参数，比如SESOI/ROPE 和先验的确定。

5 补充材料

5.1 最小感兴趣区（SESOI）与实际等价区（ROPE）的确定

在等价检验和贝叶斯估计中，都会使用一个区间来定义一个足够小的，或者说可以被忽略的效应。在等价检验中，称为最小感兴趣区（SESOI），而贝叶斯估计将其定义为实际等价区（ROPE）。其他领域的研究者还会使用其他名称，如临床领域的临床等价区间（interval of clinical equivalence）（Lesaffre 2008） 和药理学的等价区间（equivalence interval）（Schuirmann 1987） 等。但这些概念本质上是相似的，都是为了定义一个包括零效应在内的足够小的区间，或者说更符合实际研究情况的零效应。由于ROPE 与SESOI 的相似，下文将仅从SESOI 视角介绍。通过检验目标效应与该区间的相对关系可推断当前数据支持零效应、拒绝零效应还是无法做出判断（Lakens，Scheel et al. 2018，Kruschke and Meredith 2020）。当前数据的效应量区间一定时，如果SESOI 比较宽松，则效应量区间可能完全落在SESOI 内，得到支持零效应的推断；而SESOI 范围较小时，效应量区间可能未完全在SESOI 内，得到无法判断当前数据是否支持零效应的结论。因此SESOI 的设定会直接影响零效应评估的结论。

SESOI 的设定需要具体问题具体分析。但是无论使用何种方法，研究者均需要对其设定合理性进行说明（Lakens，Scheel et al.2018）。通常，当研究者所感兴趣的效应量已经有先前研究进行过探索，则可以参考先前研究的结果。例如，Simonsohn（2015）建议，在重复研究中，可将SESOI 的等价边界设置为之前研究的33%检验力可探测到的效应。其理由在于，检验力低于33%时得到的效应有多于66%的概率得到的显著结果是不可信的（Simonsohn，Nelson et al.2014）。但Simonsohn（2015）的建议并非 唯 一 的 建 议，Kordsmeyer 和 Penke（2017）则建议，在重复性研究中，可将SESOI 的等价边界设定在先前研究的平均效应量上，并检验当前数据是否显著小于之前研究平均水平的效应量。然而这种方法无法排除先前研究随机性和出版偏见的影响。此外，还有观点认为可以将等价边界设定在之前研究正好可以观测到显著效应的临界值（Lakens，Scheel et al.2018）。另一个可能更稳健的方法是用元分析中估计效应量的置信区间（90%或95%）的下边界（效应为正的情况下）作为等价边界（Perugini，Gallucci et al.2014）。最后，值得注意的是，在频率学派和贝叶斯派两种不同的统计思想的框架下，SESOI 和ROPE 对应的结果解释是有区别的（Kruschke and Liddell 2018，Kruschke and Meredith 2020）。

5.2 评估零效应的流程图

图4 评估零效应的三种统计方法的使用流程

补充材料参考文献

Kordsmeyer，T.L. & L. Penke（2017）.“The association of three indicators of developmental instability with mating success in humans.”Evolution and Human Behavior 38（6）：704-713.

Kruschke，J. & T.M. Liddell（2018）.“The Bayesian New Statistics：Hypothesis testing，estimation，meta-analysis，and power analysis from a Bayesian perspective.”Psychonomic Bulletin & Review 25（1）：178-206.

Kruschke，J. & M. Meredith（2020）. BEST：Bayesian estimation supersedes the t-Test.

Lakens，D.，et al.（2018）. “Equivalence testing for psychological research：A tutorial.”Advances in Methods and Practices in Psychological Science 1（2）：259-269.

Lesaffre，E.（2008）. “Superiority，equivalence，and non-inferiority trials.” Bulletin of the NYU Hospital for Joint Diseases 66（2）：150-154.

Perugini，M.，et al.（2014）. “Safeguard power as a protection against imprecise power esti mates.”Perspectives on Psychological Science 9（3）：319-332.

Schuirmann，D.J.（1987）. “A comparison of the two one-sided tests procedure and the power approach for assessing the equivalence of average bioavailability.”Journal of Pharmacokinetics and Biopharmaceutics 15（6）：657-680.

Simonsohn，U. （2015）. “Small telescopes：Detectability and the evaluation of replication results.”Psychological Science 26（5）：559-569.

Simonsohn，U.， Nelson，L.D.， & Simmons，J.P.（2014）. P-curve: A key to the file-drawer.Journal of Experimental Psychology General, 143（2）,534-547.