小波变换的抠图算法研究

李增禄，郭孝玉，林志兴，刘孙发，余 建，许章华

（1.三明学院 网络中心（信息化建设办公室），福建 三明 36500412.三明学院福建省资源环境监测与可持续经营利用重点实验室资源与化工学院，福建 三明 3650043.福州大学福州大学地理与生态环境研究院，环境与安全工程学院，福建 福州 350001）

将前景目标从图像中准确地分离出来称为抠图（matting），是计算机视觉任务（例如图像编辑、视频处理、目标检测）中重要的组分之一[1-3]。目前，抠图技术已经成熟地应用于网页制作、电影特效制作等领域。随着技术的进一步发展，快速、准确的抠图技术是从结构多样复杂的自然图像中提取所需前景目标的有力保障。对于给定的自然图像可以表示为前景和背景的线性组合。抠图问题就是要求解每一个像素的透明度，从而而实现精准的前景目标提取。不幸的是，抠图问题是一个严重欠约束的问题，研究人员很难根据一幅图像红绿蓝三个通道像素值集合来确定每个像元位置的三通道的前景值、三通道的背景值，以及前景与背景之间的透明度等七个未知量。为了更好地求解这个问题，早期的工作一般会通过先验知识或者统计假设的方法，例如三分图或者涂鸦，以在一定程度上降低求解的复杂性。精确的三分图的确有利于高质量抠图结果的获取。三分图中将给定的自然图像划分为前景、背景和未知区域。但是，创建三分图无疑是一项非常耗费时间和精力的工作，而且创建大规模数据的三分图的花费更加高昂。

关于小波变换[4]的工作最早出现在信号处理中。研究人员发现，在处理非平稳信号时，小波变换展现出了更为优秀的性能。在此基础上，小波变换扩展到图像处理领域，从多个尺度上分解图像信息以捕获更具代表性的图像特征。值得注意的是，小波变换能够多级展开以实现高级图像特征的捕获，同时能够保留图像的低级特征信息[5-6]。根据小波的分解系数，在重构图像信息时不仅能够保留更多的细节信息，而且也能够根据多尺度信息实现更为鲁棒的图像重构质量。

前景目标边界的精确度是影响抠图质量的重要因素之一。大部分自然图像都没有清晰的前景和背景边界。复杂的背景结构、更为接近的前景颜色和背景颜色以及背景中包含前景目标的部分结构等因素都会导致模糊的前景和背景界限[7]。此外，因为某些前景目标的独特结构，例如头发、毛发等细小的物体，或者水杯、玻璃、火焰等半透明物体，边界的透明度值很容易失真。在基于先验知识的抠图算法中，未知区域在绝大部分情况下都是标记前景对象的边界区域。基于此，我们在贝叶斯抠图算法的基础上，结合边避免小波以更好地计算前景对象的边界从而实现更为精准的抠图结果。

在本文中，边避免小波被用于处理贝叶斯抠图的滑动窗口信息，在多尺度方向上增强图像的边缘信息。在背景复杂的情况下，突出的边界信息有助于贝叶斯抠图算法采集更为鲁棒的像素点特征以实现更为理想的透明度估计。

1 相关文献回顾

在复杂背景中估计前景目标的遮罩，称为自然图像matting问题[8-10]。过去，基于采样的抠图算法和基于传播的抠图算法是估计透明度值的两种主要方法。在基于采样[11-14]的方法中，假设未知区域像素点的前景和背景都可以通过样本估计得到，采样的方法试图从给定图像的粗略划分（Trimap）的区域采集大量的样本，并按照定义的方法估计alpha，将未知像素表示为前景和背景的最佳混合。基于采样的方法从局部采样到全局采样，虽然提高了计算精度，但是其计算复杂度无疑大大增加。基于传播[15-18]的方法大多会采用局部连续性或者局部平滑性假设，通过像素之间的相似性度量将透明度值从已知区域传播到未知区域。但是，当给定的自然图像中包含大量不连续的结构，例如孔洞，基于传播的自然图像抠图算法不能达到理想的性能。

为了结合基于采样的抠图方法和基于传播的抠图方法的优势，文献[19]利用卷积神经网络融合CF（Closed-Form）抠图方法和KNN（K-Nearest Neighbor）抠图方法估计的alpha遮罩[20]以实现更为准确的遮罩估计。文献[21]基于点扩散函数恢复前景对象的模糊边界，并与经典的抠图算法结合以优化估计的透明度遮罩。文献[22]同样基于深度卷积神经网络，结合三分图先验知识估计alpha遮罩。文献[23]则认为梯度信息附近的像素信息更为关键，通过分阶段抠图的方式整合基于采样和基于传播的抠图方法的优势以实现更为精确的前景目标提取。文献[24]基于k近邻算法开发了一种自适应采样抠图算法以解决在样本缺失情况下抠图效果不佳的问题。文献[25]通过多通道抠图的方式，在不同的颜色通道中估计像素之间的亲和力以实现alpha值的传播。基于非局部原理的自然图像抠图算法采用相似采样方式，例如颜色相似性或者空间相近性实现透明度值的估计[26-29]。

线性滤波在图像处理方面有着广泛的应用[30-31]，如去除阴影，动态范围压缩等领域。依赖于数据的滤波，依靠每个像素距离中心像素的距离调整平均权重。虽然此过程不是线性的，但是这两种滤波的方法都是通过空间和频率来确定数据。基于小波变换[32]的多分辨率分析，实质上是一个线性无关变换滤波。由一对缩放函数和小波函数定义，并表现为小波变换中的卷积运算。在图像处理领域，主要利用小波变换对图像进行分解，产生一个低频分量和一个高频分量，分别对其进行处理，再经小波重构后得到我们想要的图像。通常，仅依据一层频域分解的子带分量所提供的信息，对图像进行处理是比较困难的。

将图像边缘增强同时平滑图像，称为边缘保留平滑滤波器。此方法避免了使用线性滤波器处理图像时产生的光晕伪影，在平滑彩色图像、边缘保留去噪[33]、动态范围压缩等领域有着较好的应用。文献[34]提出利用双边滤波器对线性滤波器进行扩展，包含空间和像素强度范围。通过多级策略有效地计算线性滤波，利用大内核实现双向滤波的线性计算。文献[35]利用非均匀泊松方程计算多尺度边缘平滑。文献[36]提出一种自适应地利用边缘对图像进行粗化处理。此外，文献[37]还将鲁棒平滑与提升方案[38]相结合，构建了一种新的依赖于数据的边避免小波。

Lifting Scheme是快速小波变换的有效实现，它提供了一种在没有傅里叶变换的辅助下通过空间构造正交小波的方法。在此方案中，利用一些结构简单、平移不变的双正交基，通过一系列的改进使其适应小波。此过程一般分为三个步骤：分裂、预测和更新。加权CDF(Cohen-Daubechies-Feauveau)小波(weighted cohen-daubechies-feauveau wavelets，WCDF)和加权红黑小波(weighted red-black wavelets，WRB)两种结构中的边界都很容易处理，通常用于提升方案。预测和更新操作符都仅限于域内的操作。

2 实验方法

边避免小波提升方案分为三个步骤：分裂、预测和更新。给定输入信号a[n]，将其分裂为两个不相交的集合C、F，分别为粗略和精细的数据。其中，C={(x,y)|xodd},F={(x,y)|xeven}，even表示偶数网格点集，odd表示奇数网格点集，如图1所示。使用aC[n]和aF[n]表示信号值仅限于这些集合。一个简单的方式是将数据分割为偶数和奇数网格点的集合。使用粗略的数据点aC预测精细的数据点aF，通过P:C→F表示预测算子，定义预测误差为：

图1 小波预测方案

粗略变量和精细变量在空间中混合，并且每个精细变量aF[n]在粗略变量aC[n]内具有与其预测相关的几个相邻变量。假定图像是局部相关的，预测误差d1[n]是下一级小波变幻的细节系数。通过附加更新算子u:F→C实现近似系数的总和保持稳定。该算子实现了精细变量aF到d1的平均：

新变量a1[n]为下一级小波变换的近似系数。

小波变换在数学上具有完备的分析。通过设置合适的参数，可以将小波扩展到整幅图像的不同尺度上以实现不同特征的有效提取。基于其多尺度的优点，可以粗中带细地捕获图像特征。

2.1 加权CDF小波

基于CDF小波变换，推导出沿不同轴的加权预测。没有使用粗略变量作为平均值，而是重新定义了稳健的平均值：

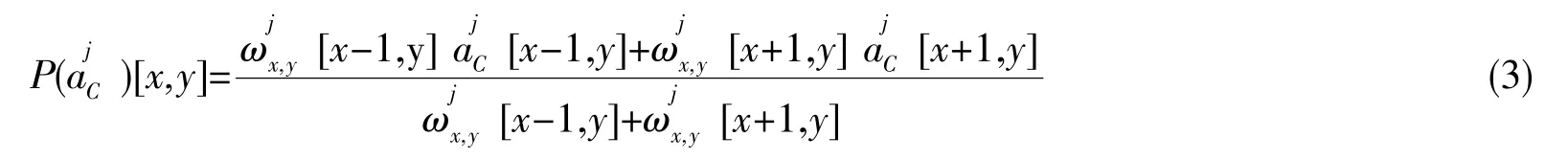
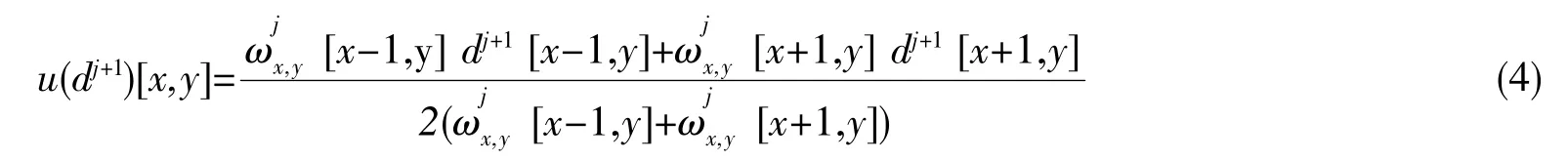
(x,y)∈C，根据式(2)计算下一级的粗略系数，其中。在图像中沿y轴重复上述步骤。

2.2 加权红黑小波

首先，利用四个最接近的黑色像素的加权平均值来预测每个红色像素

其中 Nx,y={(x+1,y),(x-1,y),(x,y-1),(x,y+1)}，(x',y')∈C。

与加权CDF小波类似，同样利用式(1)计算精确数据点的近似系数dj+1。更新算子

其中(x,y)∈C，根据式(2)计算下一级的近似系数。

其次，利用偶数坐标的四个对角线最近的深灰色邻居来预测偶数坐标的浅灰色变量。基于这种预测，在每个像素处计算。根据式(6)更新算子ublack，利用此算子使四个对角线的像素在每个浅灰色变量出平均，根据式(2)计算下一级的近似系数aj+1。

边避免小波根据输入的数据内容构建了缩放和小波函数，在提升背景的同时定义鲁棒预测算子，并根据预测像素的相似度对像素进行加权。基于预测像素与其相邻粗略变量之间的相似性使用后验影响函数，利用边缘停止函数定义预测权重：

其中，α 在 0.8到 1.2之间，ε=10-5。

对于一些粗糙级别的缩放函数，在输入图像平滑的地方可以得到平滑的轮廓。在边避免小波中，跨越边界时可以使用缩放函数表示数据中的不连续性。小波对边缘的影响减少，细节间的相关尺度增大。

2.3 解决方案

为提高机器对图像的理解，获得高质量的matting结果，利用边避免小波对图像细节进行增强。现有的一些算法，如直方图均衡、空间滤波、图像边缘锐化等，在捕获图像信息的同时可能导致图像中的噪声也得到了增强。利用小波多分辨率分析理论，多尺度对图像质量进行增强。本文基于边避免小波变换的特性，从不同尺度、多个位置和方向分析图像特征，通过调节边避免小波变换的参数以增强前景对象的边缘特征。

作为经典的抠图算法，贝叶斯抠图通过计算滑动窗口中未知像素附近的前景像素和背景像素之间的概率分布以估计未知像素的透明度值。之后，贝叶斯抠图将计算得到的未知像素的透明度值作为已知条件，逐步估计全部未知像素的透明度值。当滑动窗口中的像素更具识别性时能够更准确地计算未知像素的透明度值。贝叶斯抠图的滑动窗口是从前景目标边界的未知像素区域逐步向内部滑动，因而更为显著清晰的边界信息有助于贝叶斯抠图采集更为有效的像素特征。

贝叶斯抠图通过滑动窗口采集未知区域中的前景像素信息和背景像素信息。在采样过程中，我们利用边避免小波优化图像信息，将粗糙的信息平滑化，表示为aJ，并通过细节系数dj调节图像的平滑程度，以实现对图像细节的增强。在此过程中，考虑到YUV空间具备更好的亮度表示，更有利于边界细节的增强，因此，本文在YUV空间实现目标对象的边界优化。那么，边避免小波在YUV空间的图像分解工作可以表示为。本文通过调节多个细节指数以实现不同程度的细节增强：

实现采集信息的优化之后，贝叶斯抠图算法根据已知的前景、背景和透明度信息，通过贝叶斯定理和最大概率算法计算未知像素的透明度值：

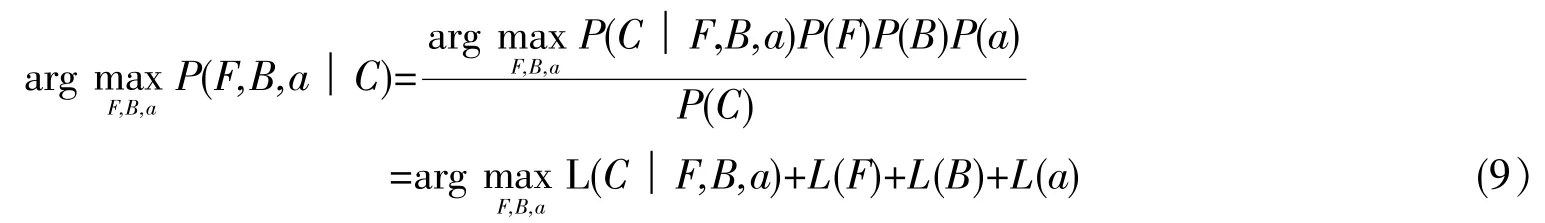
其中L(·)=lgP(·)，P(C)是一个常数。在滑动窗口采集的像素信息中，前景像素、背景像素和透明度值一般会按照高斯分布排列。在贝叶斯抠图算法中默认L(a)为常数。因此，通过贝叶斯抠图算法计算未知像素的透明度值可以简化为：

通过计算滑动窗口采集到的像素信息，建立高斯混合模型以估计未知像素的最大概率值。贝叶斯抠图算法假设符合高斯分布：

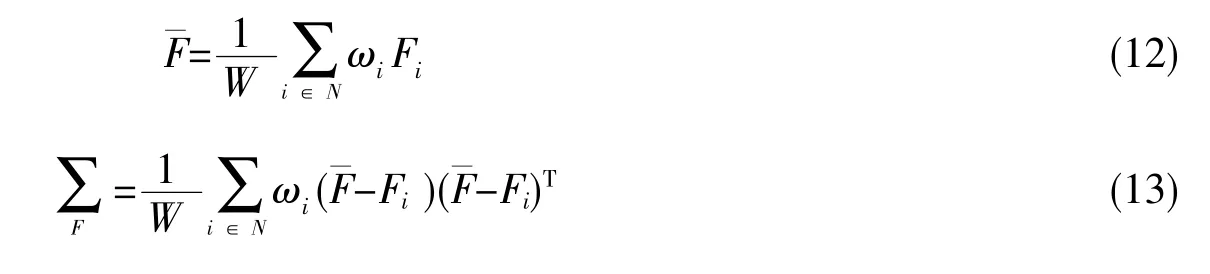
背景像素的处理方式与前景像素的处理方式极为相似，只需要将α替换为(1-α)即可。在计算出前景像素和背景像素的透明度值之后，将其带入到高斯模型之中，利用前景和背景之间的匹配寻找的最优解。

在贝叶斯抠图中，通过求解最大化公式的偏导以求解：

基于已经计算得到的前景F和背景B，可以计算得到透明度α：

通过不断的交替运算，使得最终的结果逐渐收敛于某一个值，即可得到最终的抠图结果。

3 实验结果及分析

图像的组成比较复杂，仅通过视觉观察很难得到准确的评价。定量分析的评价方法在matting效果的评价中得到广泛的应用[38-40]。我们对抠图图像基准测试集(alpha matting)[21]上的所有图像进行了实验，将部分具有代表性的图像在下文进行了表述。我们使用绝对误差和(sum of absolute difference,SAD)及均方误差(mean squared error,MSE)两种评价指标对matting结果进行评价。评价指标的计算公式为：

其中，αi是matting算法求得的结果，是测试集提供的真值结果，N为像素点的总和。样本数据在同一环境下进行处理。电脑配置如下：i9 CPU，8GB内存，NVDIA GT2080Ti显卡。

4.1 定性分析

基于贝叶斯抠图，利用边避免小波提取前景对象，在YUV空间中构建特征向量。在此基础上，提出了一种基于边避免小波的抠图方法。实验结果证明，基于边避免小波可以实现更为平滑的抠图效果。改进的方法对于复杂的前景和背景交错图像有更好的效果。我们选择一张图片进行详细比较，如图2所示。

图2 细节比较

图2中两个孩子之间的头发是交错的，绿色的头发接近背景色。从方法区域可以更为清晰地看出，CF和LB（learning based）无法有效提取区域的轮廓并将它们全部视为前景。KNN对头发轮廓的提取很好，但是，图像中有更多不连续的区域。本文使用边避免小波提取前景物体的轮廓，它在提取头发的前景和保留头发之间的轻微背景信息方面表现更好。因为绿色的头发和背景颜色差别不大，CF和LB方法只能提取大部分轮廓，导致细毛的信息丢失。KNN提取细小头发的轮廓，但是前景和背景的区分不是很好，使提取的头发轮廓变得模糊。本文的方法更适合提取边缘毛发，背景色和前景色之间的区分良好，保持细小头发的精确轮廓。

对于样本缺失的图像，本文的方法仍然可以取得较好的效果。如图3所示，在LB和CF方法中，标志部分是灰色的，表明基于采样的抠图算法对于样本缺失图像的透明度值的估计不够准确。而在KNN中，小熊手中的旗帜与本体之间存在明显的边界，在处理样本缺失的图像时未能有效提取前景对象的边界信息。在本文的方法中，旗帜与小熊本体之间的边界与地面真值更为接近。本文的方法在处理样本缺失的图像时依然能够获得更为理想的边界。

图3 样本缺失图像处理

当给定的自然图像具备较为简单的背景结构时，各种抠图算法得到的结果差别不大。 但是，本文的方法对于处理小头发很方便，即使头发区域的前景色与背景色相似。在小波优化采样的基础上，本文的方法使得前景和背景之间具备更为清晰的边界信息。在此基础上，本文的方法能够取得更为鲁棒的抠图结果。从图4中第一行和第二行展示的结果来看，本文的方法在处理前景对象边界的细小毛发时展现出更具竞争力的结果。

图4 自然图像matting比较

3.2 定量比较

对于结构复杂的自然图像，仅仅通过视觉信息判断最终结果的优劣是不够准确的。本文使用文献[30]中提供的方法来评估抠图结果。本文选择图2和图4展示的图像作为定量评估数据集，通过计算不同抠图方法获得的结果的绝对误差和(SAD)及均方误差(MSE)来评估结果。 SAD和MSE的值越小，表明抠图效果越好。图5展示了定量评估结果。可以清晰地看到，本文的方法展示出更为优越的性能。在定量评估中，无论是结构简单的图像还是图像信息缺失的图像，本文的方法都能估计出更为准确的透明度值。

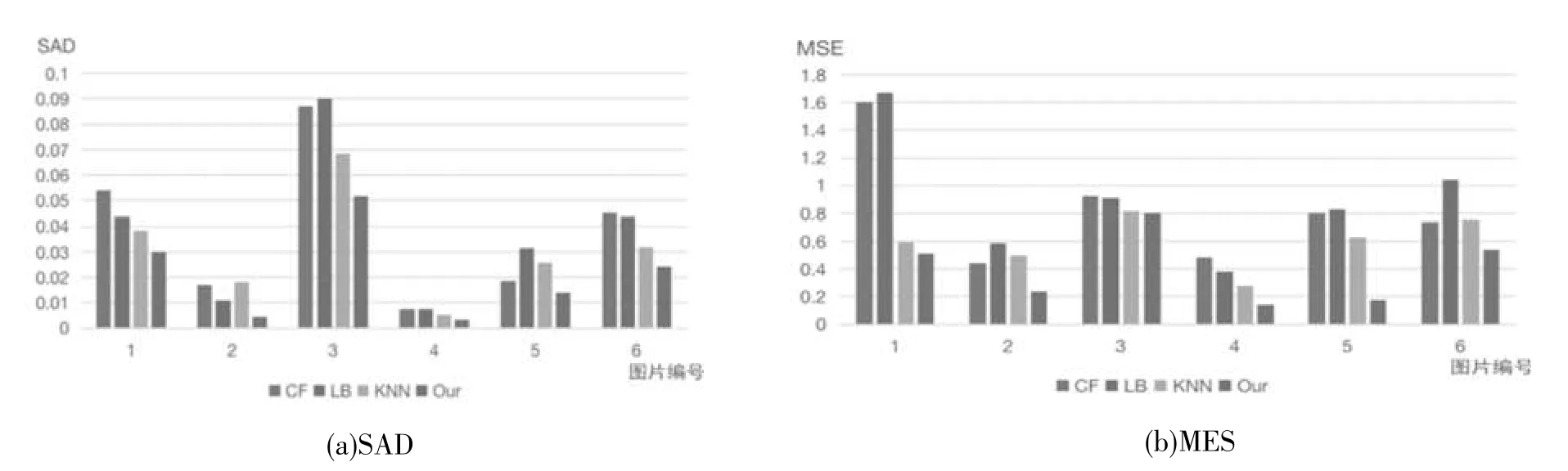
图5 测试集定量评估比较

4 总结

本文基于边避免小波的原理对自然图像进行优化以突出前景对象的边界信息。在图像处理中，小波变换能够平滑复杂的背景结构并强化弱小的边缘细节信息。本文考虑到不同色彩空间的差别，在YUV空间中优化图像的细节信息以达到更为理想的增强效果。考虑到贝叶斯抠图算法在计算不透明度值时依赖于滑动窗口采样，本文利用边避免小波突出图像的细节信息以实现更佳的采样性能。在未来，更为精确、快速的抠图算法是发展的趋势。因此，在后续的工作中尝试从不同的角度优化抠图算法是一项更具意义的工作。