体能运动训练器振动抑制的多目标优化控制

马 莉

（1.郑州西亚斯学院，河南 郑州 451150；2.河南大学，河南 开封 475000）

1 引言

体能训练在发展人体形态、运动机能以及身体素质的同时，还需要体现其功能性和指向性[1]。体能训练实际上是在身体形态、运动机能和身体素质等方面，使受训人员更好地提高维持运动的表现和日常生活中的所需[2]。体能运动训练器是实现体能训练的基础，然而随着训练器负重的不断提升，使体能运动训练器产生较大的振动位移，严重影响体能运动训练器的安全性。因此有效对体能运动训练器振动抑制进行多目标优化控制具有重要意义。

目前国内外学者对相关领域进行了研究，并取得了一定的研究成果。文献[3]方法提出了基于TMD-HMD 的海上浮式风力机主被动综合振动控制方法。

利用欧拉-拉格朗日能量方程，构建风机系统11自由度空间动力学简化模型，采用Levenberg-Marquardt算法，对平台刚度和阻尼参数进行估计。基于Van-Nguyen Dinh的方法，优化调谐质量阻尼器参数，施加主动控制力构成混合质量阻尼器，在联合载荷下，运用TMD-HMD主被动综合控制，实现风机动态响应的振动抑制。该方法能够有效减少振动能量，但该方法存在抑制振动频率较高的问题。文献[4]方法提出了基于机器视觉和改进PID的压电柔性机械臂振动控制方法。通过构建刚柔双关节机械臂实验平台进行正交试验，基于机器视觉技术对结构振动进行测量，对刚柔耦合机械臂的振动情况进行分析，确定振动控制电机参数。采用CCD相机对机械臂末端的振动图像进行采集，获取对应的振动位移。利用人工鱼群算法，优化振动抑制PID控制器参数，实现压电柔性机械臂振动控制。该方法的控制效果较好，但振动位移较大。文献[5]方法提出了基于多目标遗传算法的异步电机预测转矩控制权因子优化方法。采用多目标遗传演算法，获得一组适合于感应电动机变速驱动之模型预测转矩控制加权因子。利用转矩控制方法，最小化成本函数，并快速响应转矩、约束合并系统和无电压调制器。应用非支配排序遗传算法II，在转矩和磁链性能与系统平均开关频率之间进行转换，实现异步电机预测转矩控制优化。该方法可以同时调整多个因子，但该方法的异步电机预测转矩控制效果差。为了解决上述方法中存在的问题，提出体能运动训练器振动抑制的多目标优化控制方法。

2 体能运动训练器运动方程

主动装置的体能运动训练器系统在环境干扰力Fs(t)的作用下，通过拉格朗日方程，导出对应的运动方程，可通过下式进行描述：

式中：Ms—体能运动训练器的质量矩阵；Cs—体能运动训练器的阻尼矩阵；Ks—体能运动训练器的刚度矩阵；us(0)—体能运动训练器对应的初始位移向量；(0)—体能运动训练器对应的初始速度向量；Ds—环境干扰位置矩阵；Q(t)—控制力向量；Ps—在控制器在体能运动训练器中布置的位置矩阵。利用下述线性方程描述体能运动训练器的控制力：

式中：Gi(i=0，1，2，3)—反馈增益矩阵。结合式（1）和式（2），获得体能运动训练器的最终运动方程：

式中：P—控制器在体能运动训练器中的位置矩阵；Md—体能运动训练器对应的质量阵；Cd—体能运动训练器对应的阻尼阵；Kd—体能运动训练器对应的刚度阵。用Z描述体能运动训练器的状态向量，则体能运动训练器的状态方程如下：

式中：U—体能运动训练器的刚体运动矩阵；D—体能运动训练器的变换矩阵。通过求解上述方程，获得体能运动训练器的状态向量：

3 直流电动机模型

在体能运动训练器中直流电动机是造成振动的主要原因之一。直流电动机在体能运动训练器中由四部分构成，分别是控制线路、电机本体、逆变器和电机本体。转子的位置可以通过位置传感器获取，电机在体能运动训练器中的通态状态可以通过解码控制线路获得，逆变器中不同类型元件的通断状态可以根据电机状态进行控制。

为了对体能运动训练器系统进行分析，需要构建体能运动训练器系统的数学模型，对各量的参考方向进行确定[6-7]。

假设Lab为A相绕组与B相绕组之间存在的互感，Lac为A相绕组与C相绕组之间存在的互感，A相处对应的电压可通过下式计算得到：

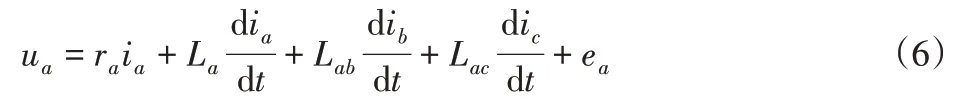
式中：ia—绕组中存在的电流；ra—绕组线圈对应的内阻；ea—反电势；ua—端电压；La—线圈自感。

同理，获得B相绕组与C相绕组处对应的电压：

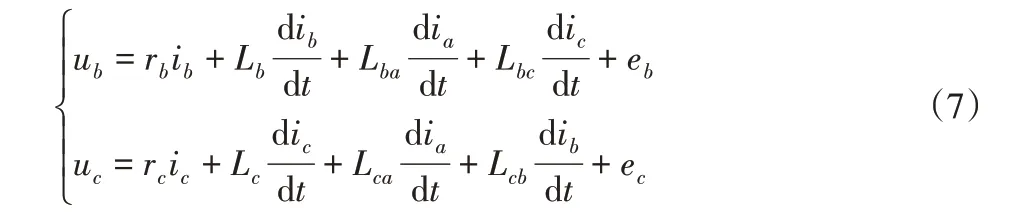
式中：Lba—B相绕组与A相绕组之间存在的互感；Lbc—B相绕组与C相绕组之间存在的互感；Lca—C相绕组与A相绕组之间存在的互感；Lcb—C相绕组与B相绕组之间存在的互感。

结合式（6）和式（7）获得直流电动机在体能运动训练器中的电压方程[8]：

三相绕组通常情况下的分布具有对称性，因此存在下式：

结合式（9）和式（10），获得下式：

因为ia+ib+ic=0，则Mib+Mic=-Mia，将其代入上式中：

设Tem代表直流电动机对应的电磁转矩，其表达式为：

式中：ω—电机在体能运动训练器的机械角速度。根据Tem构建电子转子在体能运动训练器中的运动方程为：

式中：J—负载转动惯量；λ—粘滞阻尼系数；TL—负载转矩。

4 振动抑制多目标优化控制

体能运动训练器振动抑制的多目标优化控制方法，在体能运动训练器运动方程和直流电动机模型的基础上，利用支配关系对多目标问题的最优解进行定义，从而建立体能运动训练器振动抑制的多目标优化控制模型：

式中：hj—不等式约束；gi—等式约束；h—不等式约束数量；e—等式约束数量。

设x维搜索空间的种群中存在y个粒子，vi为第i个粒子对应的速度；xi为第i个粒子对应的位置；pbesti、gbesti分别代表的是第i个粒子和所有粒子对应的最优位置，粒子在种群中通过下述公式完成速度和位置的更新[10]：

式中：r1、r2—区间[-1，1]内的常数；c1、c2—学习因子；χ—收缩因子。通过PSO算法求解优化模型的具体流程，如图1所示。

图1 算法求解流程Fig.1 Algorithm Solution Process

通过上述步骤，采用PSO算法求解优化模型，完成振动抑制的多目标优化控制。

5 实验与分析

为了验证体能运动训练器振动抑制的多目标优化控制方法的有效性，分别采用所提方法、文献[3]方法和文献[4]方法进行对比测试。将MATLAB软件作为实验平台，实验环，如图2所示。不同方法的体能运动训练器振动位移变化对比结，如图3所示。

图2 实验环境Fig.2 Experimental Environment

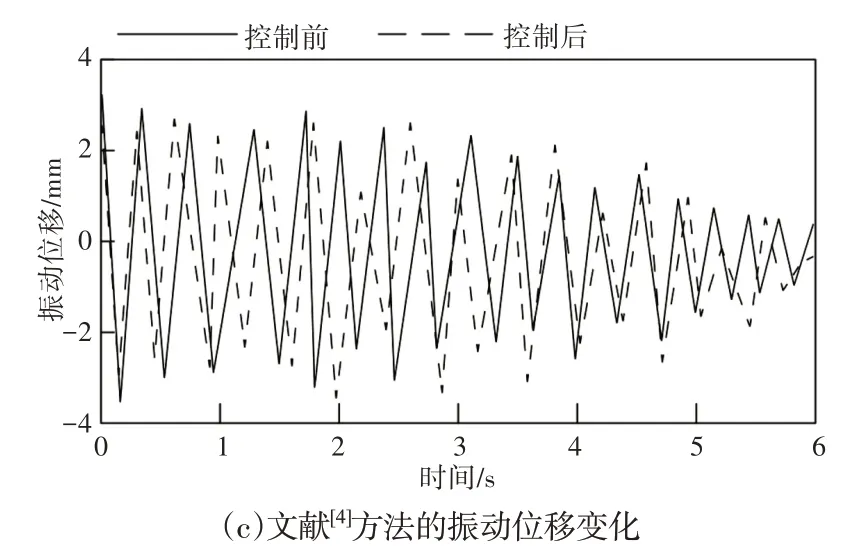
图3 不同方法的振动位移变化对比结果Fig.3 Comparison Results of Vibration Displacement Changes of Different Methods

根据图3可知，随着时间的增加，体能运动训练器的振动位移逐渐变小，对比控制前和控制后的体能运动训练器振动位移可知，采用所提方法对振动抑制进行多目标优化控制后，体能运动训练器的振动位移明显变小，采用文献[3]方法和文献[4]方法对体能运动训练器的振动进行抑制后，体能运动训练器的振动位移没有出现明显变化。

由此可知，所提方法能够有效减小体能运动训练器的振动位移。

在此基础上，为了进一步验证所提方法的体能运动训练器振幅，对比不同方法的频谱变化情，如图4所示。

根据图4可知，采用所提方法进行优化控制后，体能运动训练器的振幅明显降低，而采用文献[3]方法和文献[4]方法进行优化后，振幅虽有所降低但还是存在较大波动，对比上述方法的测试结果可知，所提方法可有效降低体能运动训练器的振动频率。

将图4中存在的峰值作为三种方法的信号强度，根据信号强度在控制前后的变化率对比所提方法、文献[3]方法和文献[4]方法的控制效果，对比结，如表1所示。

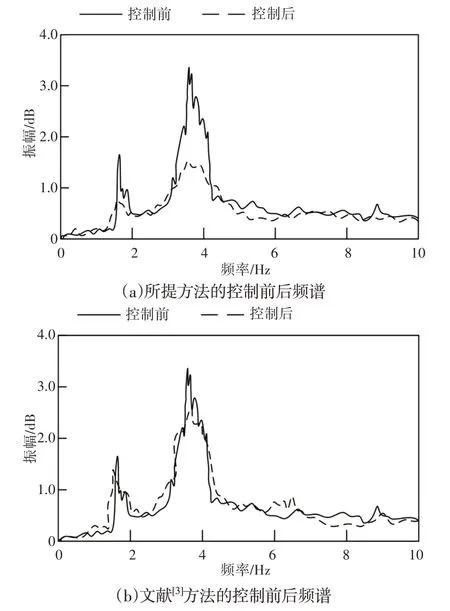
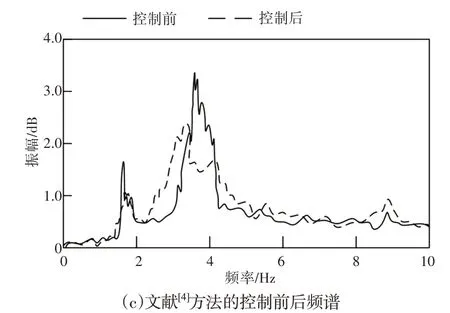
图4 不同方法的频谱变化对比结果Fig.4 Comparison Results of Spectrum Changes of Different Methods

表1 不同方法的控制效果Tab.1 Control Effects of Different Methods

根据表1中的数据可知，在多次实验中，所提方法的控制效果均高于文献[3]方法和文献[4]方法的控制效果，所提方法获得的控制效果平均值最高。

由此可知，所提方法的控制效果较好，可有效实现体能运动训练器振动抑制。

通过上述分析可知，所提方法的振动位移较小、振动频率较低、控制效果好，表明所提方法可有效实现体能运动训练器的振动抑制。因为所提方法通过建立体能运动训练器运动方程，在此基础上，结合体能运动训练器的运动方程和直流电机模型，构建多目标优化模型并采用PSO算法求解优化模型，确保了振动抑制效果，进而提高了所提方法的整体有效性。

6 结束语

提出体能运动训练器振动抑制的多目标优化控制方法。对体能运动训练器的运动状态进行分析，构建参数多目标优化模型，采用POS算法对优化模型进行求解，实现体能运动训练器振动抑制参数优化，解决目前方法中存在的问题。研究结果如下：

（1）所提方法的振动位移变化范围为（2～-2）mm，对振动抑制进行多目标优化控制后，体能运动训练器的振动位移明显变小。

（2）所提方法的最大振幅为1.5dB，能够有效降低体能运动训练器的振动频率。

（3）所提方法对体能运动训练器的振动抑制效果为92.06%。相比文献[3]方法和文献[4]方法，分别提高了12.97%和7.55%，从而确保了振动抑制效果。