直驱力矩电机双扰动位置误差预测模型研究*
2022-07-27徐祐民陈秀梅彭宝营王鹏家
徐祐民,陈秀梅,彭宝营,王鹏家
(北京信息科技大学机电工程学院,北京 100192)
0 引言
直驱力矩电机具有高精度、大扭矩、小体积等优点,在现代工业中被广泛应用[1]。但在实际生产中,由于加工及装配工艺的限制,定子、转子和转轴不可能完全重合,出现转子偏心[2]。不同程度的偏心情况会带来转矩脉动、噪声以及转子损耗增加等一系列问题[3]。针对这些问题,国内外学者进行了大量研究。任杰等[4]利用等效变换的方法,将偏心模型等效变换为永磁体剩磁重新分布的不偏心模型,结合子域法求解得到空载时偏心电机模型的气隙磁密。孔汉等[5]以卷烟自动化设备永磁伺服电机为例,采用有限元计算方法,给出了转子偏心影响气隙内谐波磁场的变化规律。SAPENA等[6]考虑了气隙长度的不均匀和所有定子和转子导体的实际位置,建立了感应电机转子偏心的快速解析模型。于嘉龙等[7]利用遗传算法优化BP神经网络,建立了永磁力矩电机偏心载荷转子位置误差的预测模型。
上述文献主要对空载时偏心电机的气隙磁场规律进行研究,少量研究考虑了偏心载荷对电机转子位置精度的影响。然而,直驱力矩电机作为机床数控转台的主要驱动部件,除了在安装时可能产生转子偏心,在加工过程中被工件材料、形状和进给量等因素影响,受到变化负载。变负载与转子偏心均可能使力矩电机位置误差增大,从而影响工件加工精度。因此,对变负载和转子偏心双扰动下直驱力矩电机的位置误差研究是必要的。本文利用人工电场算法(AEFA)优化支持向量回归(SVR)的方法,建立变负载和转子偏心双扰动下直驱力矩电机位置误差预测模型,并搭建试验台采集数据对模型精度进行验证。
1 直驱力矩电机双扰动位置误差预测模型建立方案
1.1 人工电场算法
人工电场算法(AEFA)是一种元启发式优化算法[8]。该算法模拟物理学中的库仑定律,将电荷的概念扩展到种群的适应度值[9]。AEFA算法是一个杰出的非线性优化算法,具有全局搜索能力强、避免局部解的停滞和精度高等特点[10]。
AEFA将带电粒子在静电场中的运动演化成粒子在空间中搜索最优解的过程。在搜索空间中,每个电荷代表一个可行解,其适应度由电荷量来衡量,电荷的电荷量越大,表明适应度越高。当空间中存在电荷量大的电荷时,其他电荷向电荷量大的电荷方向靠近,使算法收敛到最优解[11]。AEFA算法流程如图1所示。

图1 AEFA流程图
电荷最佳位置由式(1)确定:
(1)
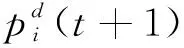
(2)

(3)
(4)
1.2 支持向量回归
支持向量回归(SVR)是支持向量机(SVM)的重要应用分支,能够很好地处理小样本数据、非线性及时间序列等问题,且具有较强的泛化能力[12]。与传统的回归方法不同,SVR引入不敏感损失因子ε,当预测值与目标值差别的绝对值小于ε时认为预测正确,不会计算损失[13]。SVR构造预测问题的标准形式为[14]。
(5)
(6)
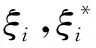
(7)
式中,α为拉格朗日乘子;K(xi,x)代表核函数。其中惩罚因子C与核函数中的核函参数g对决策函数的结果具有重要的影响,本文使用AEFA对这两个参数进行优化。
1.3 建立AEFA-SVR直驱力矩电机双扰动位置误差预测模型
力矩和电流是影响电机位置精度的主要因素,以力矩和电流作为输入,电机位置误差作为输出,利用AEFA算法优化SVR中的主要参数惩罚因子与核函参数,建立AEFA-SVR直驱力矩电机双扰动位置误差预测模型,预测模型建立流程图如图2所示。
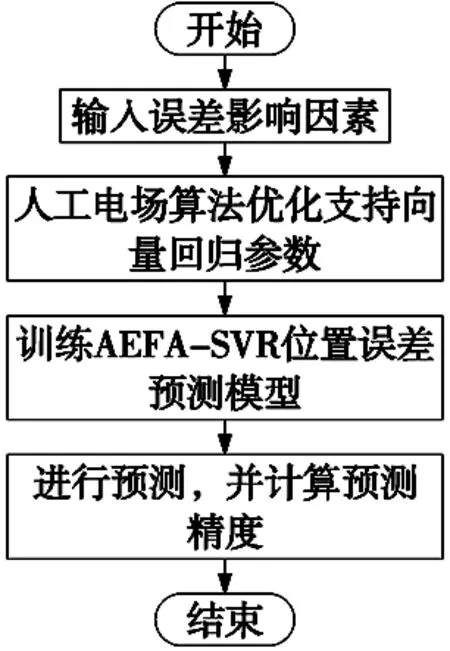
图2 AEFA-SVR电机位置误差预测模型流程图
2 AEFA-SVR误差预测模型训练及实验结果分析
2.1 样本实验数据采集
直驱力矩电机双扰动位置误差采集实验平台分为:控制系统、采集系统和运动系统三部分。控制系统包括上位机、IMAC400运动控制卡、大族伺服驱动器和数据总线;运动系统包括CD-HSY-5磁粉制动器、大族FI1-005有框力矩电机和固定支架等;采集系统包括圆光栅编码器、DYN-005力矩变送器和USB5935数据采集卡等。实验台部分结构如图3所示。

图3 实验台部分机构图
在上位机的PEWIN32PRO软件中编写直驱力矩电机的运动指令,IMAC400运动控制卡和电机驱动器完成A/D信号转换,实现电机的位置运动控制。直驱力矩电机的检测系统将电机的实际运动位置、实际电流和速度发送到上位机,实现在线补偿。通过在转子外侧放置质量块的方式模拟电机转子偏心。经多次实验,放置0.4 kg左右质量块有较好的模拟效果。磁粉制动器与电机通过联轴器连接,利用磁粉制动器加载电流的变化实现变负载工况模拟。
力矩变送器采集到的可变力矩,通过USB5935数据采集卡上传到上位机。利用LabView编写的采集系统,查看并保存力矩数据。电流与位置误差通过HMServo软件查看并保存。
采集得到的数据经处理后剩余200组,如图4所示。由图4可知,在力矩发生突变时,力矩电机的位置误差会显著增加。
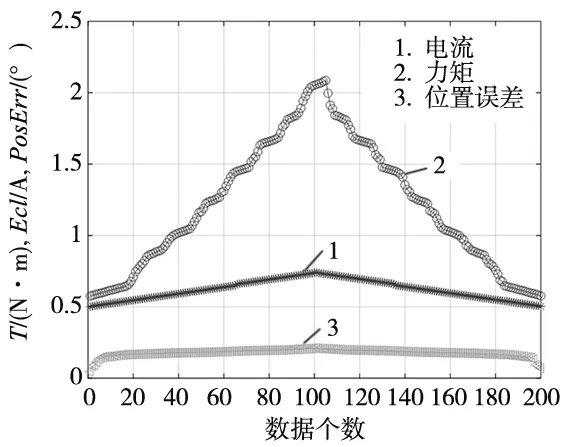
图4 处理后数据
将质量块取下,在相同的变载荷加载条件下得到电机无偏心情况下位置误差数据,与偏心下位置误差数据进行对比,得到图5。由图5可知,转子偏心状态下,电机位置误差明显增大。
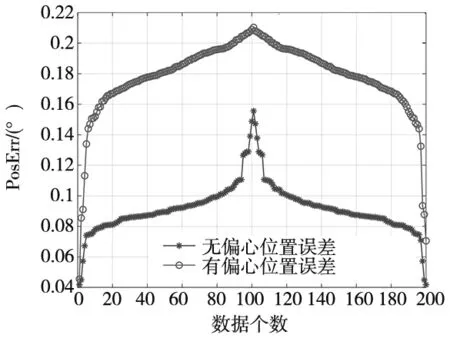
图5 转子偏心与无偏心下电机位置误差对比
2.2 预测数据分析
因采集得到的数据维度不同,可能导致预测模型训练时间变长、预测精度下降,所以对数据进行归一化处理,将电流、力矩和位置误差数据的范围变成[-1,1]。
本文建立AEFA-SVR直驱力矩电机双扰动位置误差预测模型和SVR直驱力矩电机双扰动位置误差预测模型进行预测效果对比。将实验得到数据集分为训练样本与测试样本,其中训练样本对预测模型进行训练,测试样本检测预测模型精度。在处理后的200组数据中,随机抽取20组作为测试样本,剩余180组作为训练样本。
在AEFA中设置粒子(电荷)数为60,最大迭代次数为400次,对SVR的惩罚因子和核函参数进行优化求解,得到结果如表1所示。

表1 AEFA优化结果表
将优化得到的参数写入AFEA-SVR预测模型中,对模型进行训练并将测试样本输入进行精度验证,结果如图6所示。
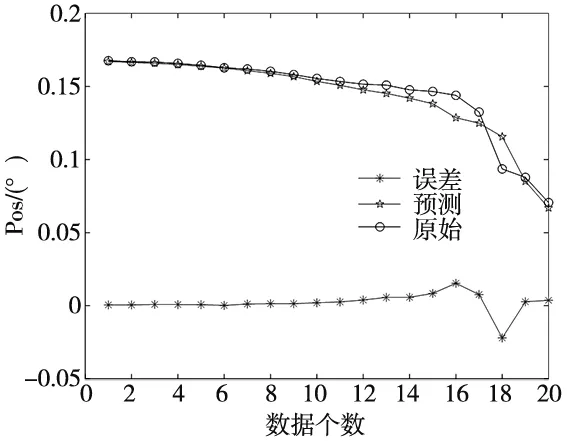
图6 AEFA-SVR预测模型实验验证结果图
图6中,AEFA-SVR预测模型最大预测误差在第18个数据点,最大误差为-0.022 1°;最小预测误差点在第6个数据点,最小误差为1.88×10-4°。
设置SVR模型的惩罚因子C和核函参数g分别为1.25和1.4,将训练样本输入对SVR神经网络进行训练,测试样本输入进行模型精度验证,结果如图7所示。
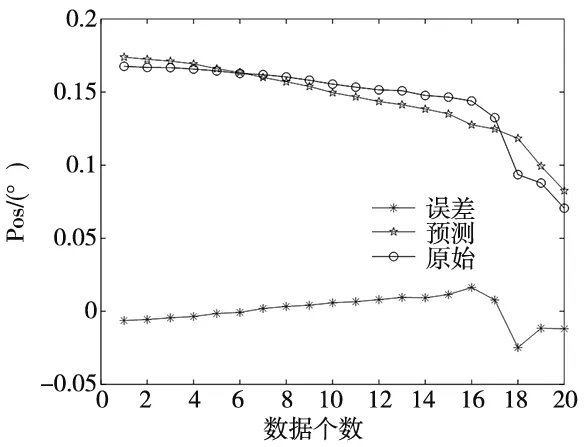
图7 SVR预测模型实验验证结果图
图7中,SVR预测模型最大预测误差出现在第18个数据点,最大误差为-0.024 8°;最小预测误差出现在第5个数据点,最小误差为-0.001 5°。
实验验证两种预测模型精度对比如表2所示。通过对比,AEFA-SVR位置误差预测模型各项数据优于SVR位置误差预测模型。说明人工电场算法具有良好的优化效果,并且建立的位置误差预测模型具有较高的预测精度。

表2 两种预测模型预测精度对比
3 结论
本文采用AEFA-SVR与SVR两种方法建立直驱力矩电机双扰动位置误差预测模型。搭建试验台,采集电流、力矩和位置误差数据。在相同加载方式下,对比转子偏心和无转子偏心的位置误差,说明转子偏心对力矩电机位置精度有较大影响。利用采集的数据对两预测模型进行精度验证。实验结果表明,AEFA-SVR位置误差预测模型最大误差-0.022 1°,最小误差1.88×10-4°,平均绝对误差0.044°,均方根误差0.036%,拟合度95.3%,各项数据均优于SVR位置误差预测模型,说明AEFA-SVR位置误差预测模型预测效果较好。直驱力矩电机双扰动位置误差预测模型的建立,有助于机床直驱数控转台位置误差的补偿研究,也有利于机床加工精度的提高。
