箱体零件辅助加工时间建模及工步排序优化*

张胜博，张 松

(山东大学a.高效洁净机械制造教育部重点实验室；b.机械工程国家级实验教学示范中心，济南 250061)

0 引言

箱体零件被广泛用于各类工程机械领域，具有结构复杂、工艺特征多等特点，传统加工工艺在加工复杂箱体零件时往往存在加工效率低和多次装夹难以保证精度等问题。立卧镗铣加工中心可实现一次装夹下，完成多面多孔的高效加工，并提高加工精度，然而装夹次数的减少使得每次装夹下的工步数增多，难以安排合适的工步顺序，且立卧镗铣加工中心的双主轴结构与多轴联动功能使得工步之间的辅助加工时间关系较为复杂，加工效能难以最大限度的发挥。工艺路线优化是计算机辅助工艺设计(computer aided process planning,CAPP)系统的核心部分，可在明确零件的工艺特征和加工方法的基础上，进行工步的排序。其目的是合理安排加工顺序，在满足零件特定加工顺序原则的前提下尽量提高加工效率。因此，分析箱体零件在复合加工中心上的加工方式并研究工步排序方法具有重要的工程价值。

目前，国内外已有很多学者对加工工艺路线的问题进行了研究，并将一些智能优化算法，如蚁群算法(ant colony optimization,ACO)[1]、粒子群算法(particle swarm optimization,PSO)[2-3]和遗传算法(genetic algorithm,GA)[4-5]等应用到排序问题上，其中GA的应用最为广泛。利用GA进行路线寻优的关键在于保证优化结果的可行性，即满足工艺约束。SU等[6]提出一种基于遗传算法的边缘选择策略，以此在种群初始化过程中产生可行解，进而求解最佳工步顺序；HUANG等[7]以生产成本为目标，借助工序优先图(operation precedence graph,OPG)产生可行操作序列，并提出了基于混和遗传算法和模拟退火算法的工步排序优化方法；KLINDWORTH等[8]针对汽车工业实践，提出了一种基于对可行性工序序列(feasible operation sequence,FOS)学习的OPG生成方法，获得了比较真实的优先图；郭祥雨等[9]针对同一特征的多种加工方法，在免疫遗传算法的基础上，利用前趋图描述工步关系，并通过加工实例验证了算法的有效性；CHAUBE等[10]以生产时间和成本为目标，采用NSGA-2算法获得了工序序列的帕累托解，用以指导实际加工；窦建平等[11]以总成本为目标，利用OPG描述工序间的优先关系约束，提出了新型的面向FOS的遗传算法。YUN等[12]提出了一种混合遗传算法的概念和自适应局部搜索方法，对FOS的解空间展开搜索并获得了优质解。上述方法均可得到可行的工艺方案，但在运算前需要构建工序优先图、前趋图等用以描述工步间优先关系的有向无环图，人工参与程度较大，且面对工步数过多的复杂零件难以应用。

在已有的工步排序优化研究中，大多以单主轴数控机床为研究对象建立目标函数模型。本文在分析典型箱体零件加工特征的基础上，面向立卧双主轴复合加工中心，提出了合理的辅助加工时间计算方法，并建立了工步排序优化模型，同时借助多色集合理论(polychromatic set theory，PST)定义工步间的约束关系以确保优化结果的可行性，降低了人工参与程度。最后使用改进的遗传算法进行工步顺序优化，获得了辅助加工时间最短的工步排序方案，有效的降低了箱体零件在加工过程中的辅助时间，提高了生产效率。

1 典型零件工艺特征

本文研究的典型箱体零件的三维模型及特征标注如图1所示，其中同一加工方位上相同精度、相同几何尺寸的特征合并为一个特征。

(a) 特征标注图A (b) 特征标注图B

该零件可在立卧镗铣加工中心上一次装夹下进行的工步数为44个，基于零件的加工要求安排合适的刀具和加工方法。零件特征及对应工步见表1，其中加工方位表示刀具的进刀方向。

表1 零件特征及对应工步

2 数学模型建立

2.1 立卧镗铣加工中心描述

相比于传统三轴加工中心，立卧镗铣加工中心采用了双主轴双通道的工作方式，增加了工作台(C轴)的旋转和V轴、W轴的平动功能，以及卧式主轴的加工功能，具备一次装夹下实现多个平面和孔系加工的能力。复合加工中心示意图如图2所示，相关参数如表2所示。

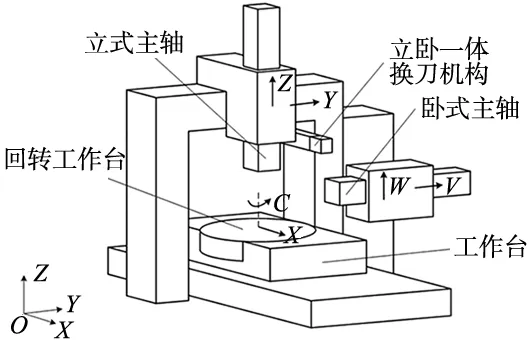
图2 立卧镗铣加工中心示意图

表2 立卧镗铣加工中心相关参数

续表

2.2 辅助加工时间计算

相邻工步之间的辅助加工时间包括立式主轴快速移动时间、卧式主轴快速移动时间、工作台转位时间与换刀时间。其中，主轴快速移动时间指主轴往返于换刀位置与加工位置所需时间，可视为定值。根据复合加工中心工作方式确定辅助加工时间4个部分之间的关系：

(1)各进给轴与回转轴之间可实现多轴联动，立式主轴与卧式主轴的快速移动可并联进行。

(2)换刀操作与主轴快速移动串联进行，并可与异主轴快速移动、工作台转位或异主轴加工并联进行。

(3)为避免刀具与工件产生干涉，主轴快速移动与工作台转位串联进行。

零件加工时以方位6为装夹面，方位1上的特征由立式主轴加工，方位2～5上的特征通过旋转工作台与卧式主轴加工。设Pi为第i个工序的加工方位，则相邻工步之间的辅助加工时间计算如下：

当相邻两工步均为立式加工，即Pi=Pi+1=1时：

tA(i)=(tV+tT)×λ(Ti+1,Ti)

(1)

式中，tA(i)为该情况下相邻工步之间的辅助加工时间；tV为立式主轴快速移动时间；tT为换刀时间；Ti为第i个工序所使用的刀具编号，且满足：

(2)

当相邻两工步均为卧式加工，即Pi≠1且Pi+1≠1时：

tA(i)=k×tH+max[tP×μ(Pi+1-Pi),tT×λ(Ti+1,Ti)]

(3)

式中，tH为卧式主轴快速移动时间；tP为工作台旋转90°时间，且满足：

(4)

(5)

当相邻两工步依次为立、卧式加工，即Pi=1且Pi+1≠1时：

(6)

当相邻两工步依次为卧、立式加工，即Pi≠1且Pi+1=1时：

(7)

综上所述，辅助加工时间可表示为：

(8)

式中，n为该道工序中所包含的工步数。

2.3 基于多色集的约束矩阵模型

2.3.1 多色集合理论

多色集合理论是一种信息处理的数学工具，利用围道矩阵来描述系统中元素的组成结构以及元素性质之间的映射关系[13]。

若记加工方法集合为A={a1,a2,…,ai}，加工特征集合为F(a)={F(a1),F(a2),…,F(ai)}，加工方法ai对应的特征记为Fj(ai)，则可以将两者之间的关系用围道矩阵A×F(ai)表示：

(9)

式中，若ai∈F(ai)，则cij=1；若ai∉F(ai)，则cij=0。

2.3.2 约束矩阵构建

加工中心单次装夹下的工步顺序主要受两个条件的约束：①先粗后精原则，即加工某一表面时应按粗加工-半精加工-精加工的顺序进行；②先面后孔原则，即对于有孔特征位于面特征上的零件，应该先铣面，后镗孔或钻孔[14]。

根据工步间的优先关系原则，利用多色集合理论建立工步优先关系约束矩阵。设零件有u个特征，v种加工方法，则建立式(9)形式的“特征-方法”矩阵av×u和“特征-孔数”矩阵bw×u，其中w为单一面特征上包含的孔特征的最大数目，并对其进行着色和工步号编码，得到围道矩阵。

接下来进行工步优先关系约束矩阵编码。建立“工步-工步”矩阵M=[sij]n×n如下：

(10)

n为零件加工所需工步数，利用工步之间的顺序约束关系填充矩阵，若工步OPi必须在工步OPj之后完成，则sij=1；否则sij=0。

约束矩阵编码方法如下：

步骤1：输入“特征-方法”矩阵，以每一特征中优先级低的加工方法对应的工步号为行数，优先级高的加工方法对应的工步号为列数，将“工步-工步”矩阵中相应位置的值置为1。

步骤2：输入“特征-孔数”矩阵和“特征-方法”矩阵，以孔特征所需加工方法对应的所有工步号为行数，所在面特征所需加工方法对应的所有工步号为列数，将“工步-工步”矩阵中相应位置的值全部置为1。

3 改进的遗传算法流程

3.1 解的编码

本文采用实数进行编码，设有n个工步，则每条染色体由[1,n]范围内的不重复的整数组成。为保证染色体符合工步优先关系约束，利用约束矩阵校验随机生成的染色体，将不符合约束的基因值依次对调。

3.2 适应度值计算

首先构建工步的资源矩阵，工步与矩阵信息的映射关系如下所示：

j→{OPj,Tj,Pj},j=1,2,…,n

(11)

式中，OPj、Tj、Pj分别为第j个工步对应的工步编号、刀具编号和加工方位，然后以2.2节中方法计算辅助加工时间，并以其倒数作为遗传算法的适应度值。

3.3 精英选择操作

选择操作是遗传算法中保留优质染色体的主要方法，通常使用轮盘赌方式进行个体的选择，设种群大小为N，个体xk的适应度为F(xk)，则个体进入下一代的概率Pk为：

(12)

为保证最优个体能够被选择从而加速算法收敛速度，本文在选择操作中引入精英保留策略，即先保存每一代种群中适应度最高的精英个体，在选择、交叉、变异操作后，用精英个体替换掉新种群中适应度最低的个体。

3.4 交叉和变异算子

交叉和变异是遗传算法中产生新个体的主要方式。为保证交叉和变异后的染色体仍符合工步优先关系约束，同时减小算法的计算负担，设计了片段交叉算子和片段变异算子。

图3 片段交叉算子 执行过程

图3为片段交叉算子的执行过程，其输入为两个父代染色体P1、P2，输出为子代染色体O1、O2。在P1中随机生成两个交叉位置j和k，两交叉位置之间的部分称为交叉片段，将P1中交叉片段内的基因按照P2中的顺序调整后置入O1中对应位置，同时将交叉片段以外的基因按原顺序置入O1。交换P1、P2的角色可获得另一个子代染色体O2。

图4 片段变异算子 执行过程

图4为片段变异算子的执行过程，其输入为变异前的染色体P，输出为变异后的染色体O。在P中随机产生一个变异位置m，从m位置向后寻找第一个违背工步优先关系约束的基因，记其位置为n；将m处的基因值插入到n处之前；片段中其余基因依次前移。

3.5 自适应的交叉和变异概率

合理的交叉概率Pc和变异概率Pm是保证种群多样性和确保遗传算法收敛的关键，为在保证收敛的前提下提高寻优能力，引入交叉概率Pc和变异概率Pm可随适应度变化而进行调整的自适应方法，两者的计算方法如式(13)、式(14)所示：

(13)

(14)

式中，fmax为当前种群个体的最大适应度值；favg为当前种群的平均适应度值；f′为交叉的两个染色体中适应度值较大的染色体；f为待变异的染色体的适应度值；Pc1、Pc2、Pm1、Pm2为介于0和1之间的常数。

3.6 算法流程及实现

算法参数包括种群规模NM、最大进化代数GN、染色体长度LN、最大交叉率Pc1、最小交叉率Pc2、最大变异率Pm1、最小变异率Pm2，其中LN的大小等于工步数，NM应为偶数。算法流程及实现过程如下：

步骤1：初始化参数。

步骤2：使用randperm函数随机生成包含NM个染色体的初始种群，并利用约束矩阵保证每条染色体都符合优先关系约束。

步骤3：计算种群中每个个体的适应度值。

步骤4：利用精英保留策略进行选择操作。

步骤5：利用自适应的交叉和变异算子进行交叉变异操作。

步骤6：重复步骤3～步骤5，迭代循环至最大进化代数GN，得到最佳工步排序方案。

4 典型箱体零件工步排序优化实例

4.1 基于多色集的约束模型分析

为描述箱体零件先粗后精的约束条件，利用多色集合理论建立表3所示的“特征-方法”围道布尔矩阵并进行工步号编码，得到表4，表中F1～F26分别代表第1～第26个加工特征，O1～O8分别表示粗铣、精铣、钻孔、攻丝、反刮孔、粗镗、半精镗、精镗等8种加工方法。

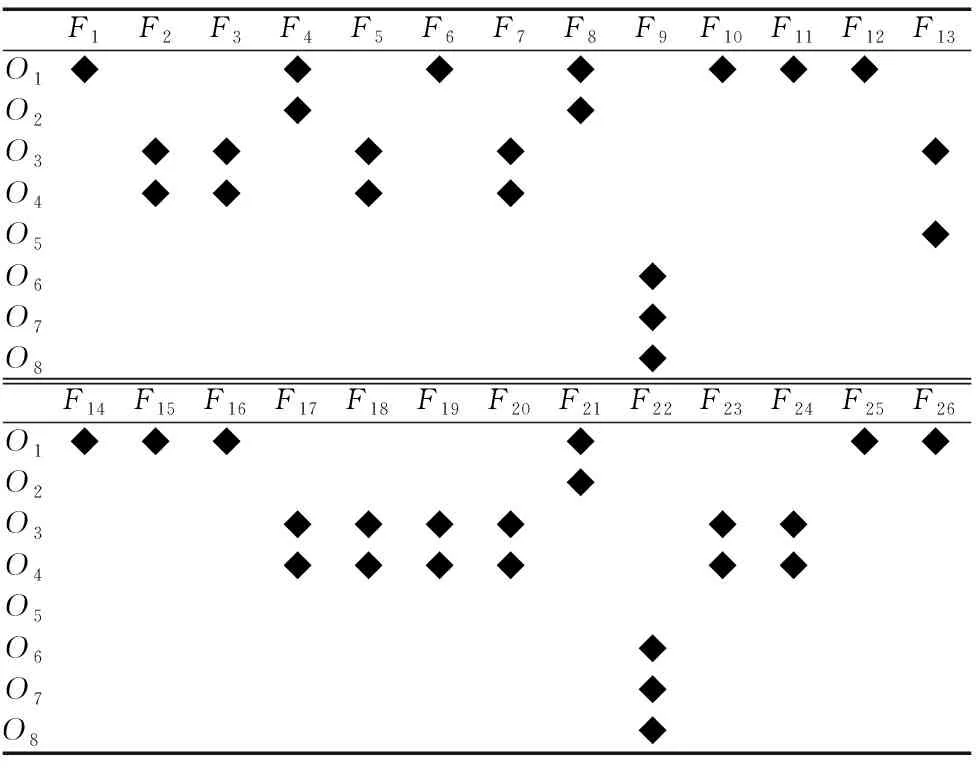
表3 “特征-方法”围道矩阵

表4 “特征-方法”围道矩阵工步编号

续表

为描述工步排序中的先面后孔约束条件，建立表5所示“特征-孔数”围道布尔矩阵并编码得到表6，表中F1～F26代表第1～26个加工特征，H1～H2分别表示面特征上的第一、第二个孔特征。

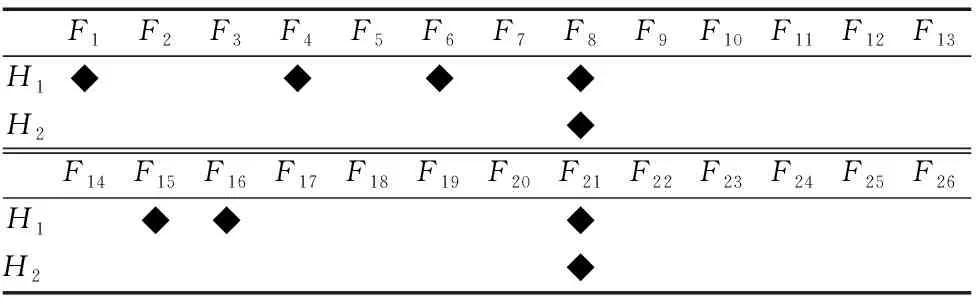
表5 “特征-孔数”围道布尔矩阵

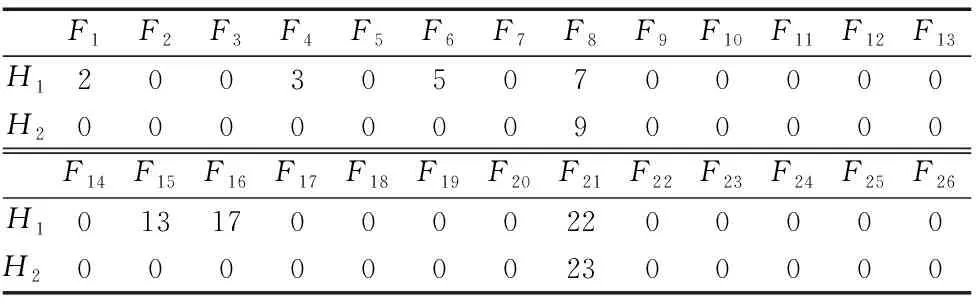
表6 “特征-孔数”围道布尔矩阵特征编号

最后利用“特征-方法”和“特征-孔数”矩阵，编码得到式(10)形式的44×44的“工步-工步”约束矩阵M。

4.2 优化结果及分析

按照算法流程对图1所示箱体零件的工步顺序进行求解，算法参数设置如下：种群规模NM=100，染色体长度LN=44，Pc1=0.9，Pc2=0.5，Pm1=0.1，Pm2=0.001，最大进化代数GN=1000。设定立式主轴的快速移动时间为6 s、卧式主轴的快速移动时间为5 s、工作台转位90°时间为3 s、换刀时间为5 s。最短辅助加工时间为目标进行优化，运算后得到的最短辅助加工时间为248.5 s，对应的最优染色体基因表达形式如图5所示。

图5 最优染色体表达

4.3 对比实验

为验证本文改进遗传算法的优越性，仍以图1所示箱体零件为目标，将本文算法与标准遗传算法进行比较。由于遗传算法的随机性，连续进行10组对比试验并记录其结果。其中，第一组实验的对比收敛图如图6所示，10组实验的结果如表7所示。

图6 优化对比图

表7 实验结果对比 (s)

对比结果表明，本文采用的改进遗传算法相比于标准遗传算法具有运算时间短、收敛速度快的优势，说明了本文设计的运算算子的有效性，改进的遗传算法在处理工步排序问题时具有一定的优越性。

5 结论

本文面向立卧镗铣加工中心加工复杂箱体零件时的工步排序问题开展研究，通过分析立卧镗铣加工中心的工作方式建立了辅助加工时间模型，并基于多色集理论构建了约束矩阵模型；随后在标准遗传算法中引入了自适应算子来提高寻优能力，并设计了交叉算子和变异算子以减少算法的运算负担，提高运行效率。利用典型箱体零件实例进行验证，得到合理可行的辅助加工时间最短的工步顺序，并通过对比证明了优化方法的有效性。