基于GSA-VMD和自适应CNN的滚动轴承故障诊断*

王亚辉，刘德平，王 宇

(郑州大学机械与动力工程学院，郑州 450001)

0 引言

轴承是机械装置的关键零部件之一。如果轴承出现故障，则会严重影响机械装置的可靠性与稳定性，甚至造成巨大的经济损失，威胁人员的生命健康[1]。因此，研究滚动轴承的故障诊断方法具有重要意义。

轴承故障诊断的关键在于提取故障特征与模式识别。而轴承的振动信号往往具有非线性与非平稳的特性，难以提取故障特征[2]。经验模态分解[3](EMD)、局部均值分解[4](LMD)、变分模态分解[5](VMD)等是处理非线性与非平稳信号常用的方法之一。但EMD与LMD容易受模态混叠与端点效应的影响[6]。变分模态分解(VMD)具有可靠的理论基础，能有效抑制模态混叠与端点效应。但VMD的模态分解个数K与惩罚因子α严重影响信号的处理结果[7]。孟宗等[8]采用VMD分解轴承振动信号后，产生的模态分量(IMF)的能量占比，判断模态分量的个数K，进而提取故障轴承的故障频率，判断故障类别。吕阳等[9]采用正交实验的方法确定VMD的模态分解个数K与惩罚因子α，实现轴承的故障诊断。因此，VMD算法的关键在于确定恰当的参数组合[K,α]。

卷积神经网络(CNN)是深度学习的一种方法，具有良好的特征提取能力，适用于轴承诊断的模式识别[10]。ZHANG等[11]将深度卷积神经网络(DCNN)应用到旋转机械的故障诊断，具有良好的抗干扰性。DING等[12]改进CNN的结构，研究了一种多尺度卷积自编码故障诊断方法，实现对轴承的故障诊断。但针对不同的故障诊断问题，需要反复试验与调试，才能确定卷积神经网络的超参数，建立CNN诊断模型。

为解决VMD的参数选择与CNN架构难以确定的问题，研究一种GSA-VMD和自适应CNN的滚动轴承故障诊断方法。首先采用引力搜索算法[13](GSA)优化VMD的参数，然后分解轴承的振动信号，得到若干模态分量，结合振动信号构建特征矩阵，最后利用粒子群算法[14](PSO)自适应地确定CNN的架构，构建CNN诊断模型，实现轴承的故障诊断。

1 理论基础

1.1 变分模态分解

变分模态分解(VMD)详细分解过程见文献[5]。VMD主要采用维纳滤波和希尔伯特变换的方法构造变分模型，如式(1)所示，然后将原信号f(t)分解成K个模态分量(IMF)。

(1)

为求解变分模型，引入惩罚因子α和拉格朗日乘子λ(t)，利用增广的拉格朗日将约束的变分问题转化为非约束的，表达式如式(2)所示。

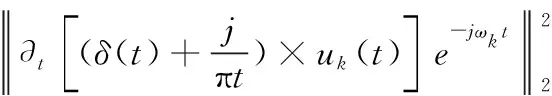
(2)

式中，α为惩罚因子；λ(t)为拉格朗日乘子。

采用交替乘子法(ADMM)求式(2)的鞍点，即为式(1)的最优解。式(2)中，uk、ωk的更新过程如式(3)、式(4)所示。

(3)

(4)

1.2 引力搜索算法

引力搜索算法(GSA)的主要步骤如下：

步骤1：在d维搜索空间中，初始化粒子与速度。

(5)

步骤2：计算粒子的适应度值fiti(t)，更新优质粒子best(t)与劣质粒子worst(t)，对于求最小值问题，best(t)和worst(t)定义如式(6)所示。

(6)

步骤3：更新引力系数G(t)，计算粒子的惯性质量mi(t)，被动引力质量Mp(t)，主动引力质量Ma(t)。

(7)

(8)

式中，G0为t0时刻的万有引力常量；β为衰减系数；T指最大迭代次数；Mi(t)为归一化后的惯性质量。

(9)

(10)

(11)

步骤6：若满足终止条件，输出最优结果，否则转向步骤2。

1.3 卷积神经网络

卷积神经网络(CNN)是专门用于处理具有类似网格结构数据的网络，具有强大的特征提取能力[15]。卷积层(conv)、池化层(pool)与全连接层(FC)是卷积神经网络三种主要类型的层。在卷积层中，上一层的输出与卷积核进行卷积，激活后输出特征图，计算过程如式(12)所示。池化层主要是降低前一层的维数，防止过拟合，该过程如式(13)所示。全连接层将输出矩阵转化为一维特征向量，然后输入到分类器，其计算过程如式(14)所示。

(12)

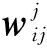
(13)

式中，β为权值矩阵；down(·)为降采样函数。

Xl=f(b0+w0·fv)

(14)

式中，fv为特征矢量；w0、b0分别为权值矩阵和偏置矩阵。

2 构建轴承故障诊断模型

2.1 GSA优化VMD算法

由式(1)和式(2)知，在变分模态分解中，为获得良好的信号处理结果，必须合理设置惩罚因子α与分解个数K。因此，采用GSA优化VMD的参数。

采用GSA优化VMD，首先选择适应度函数。原信号经VMD分解后，若各模态分量规律性强，含有的噪声越少，则信号越稀疏。而包络熵反映信号的稀疏性，熵值越小，信号越稀疏，信号包络熵的计算如式(15)所示。因此，将包络熵作为GSA优化VMD的适应度函数。然后利用GSA优化VMD算法中的惩罚因子α与分解个数K，找到最优的参数组合[α0,K0]，该过程具体流程如图1所示。

(15)

式中，a(j)为原信号经希尔伯特变换后得到的包络信号；pj指包络信号归一化；Ep为模态的包络熵。

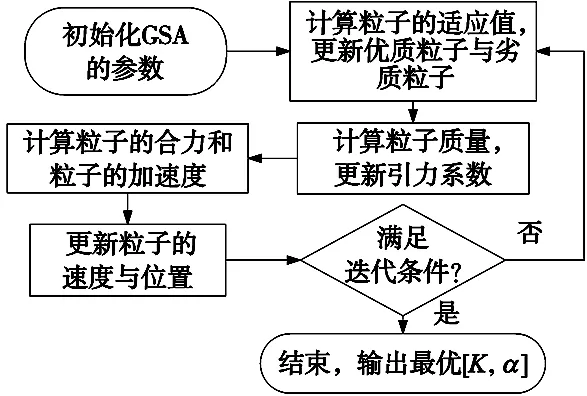
图1 GSA优化VMD流程图

2.2 构建自适应CNN模型

自适应CNN模型主要采用粒子群优化算法(PSO)，适应性选取CNN的层数、池化层的类型、卷积核尺寸、卷积核个数，全连接层神经元的个数等超参数，其主要流程如图2所示。

图2 自适应CNN模型流程图

具体步骤如下：

步骤1：获取样本集，并归一化处理样本数据；

步骤2：确定适应度函数。文中的适应度函数为交叉熵损失函数，如式(16)所示；

(16)

步骤3：初始化CNN模型参数，即确定适当的粒子个数、迭代次数、惯性系数，加速度系数，网络层的区间，卷积核的区间、池化层的类型、全连接层神经元的范围、输出层神经元的个数；

步骤4：PSO优化选取CNN的超参数，即按照每个粒子的适应度值，寻求粒子群的局部最优位置pbesti与全局最优位置gbesti，按照式(17)与式(18)更新粒子的位置；

vi+1=ωvi+c1r1(pbesti-xi)+c2r2(gbesti-xi)

(17)

xi+1=xi+vi+1

(18)

式中，vi为第i个粒子的速度；xi为第i个粒子的位置；ω为惯性权重；c1、c2是学习因子；r1、r2是0～1内的随机数。

步骤5：如果满足迭代条件，终止迭代，否则返回步骤4；

步骤6：利用PSO寻优结果，构建CNN模型。

2.3 轴承故障诊断模型

GSA-VMD与自适应CNN的轴承故障诊断模型的主要步骤如下，流程图如图3所示。

步骤1：采集轴承的诊断信号；

步骤2：采用GSA优化VMD的参数，然后利用优化的VMD将振动信号分解为若干模态分量；

步骤3：将模态分量与振动信号联合构建样本集；

步骤4：采用PSO适应性选取CNN的超参数，然后，构建CNN诊断模型，并测试模型的性能；

步骤5：输出诊断结果。

图3 故障诊断模型流程图

3 实验验证

3.1 实验数据

实验数据源自某大学(CWRU)的滚动轴承数据[16]，采样频率为1024 Hz。诊断的滚动轴承型号为：深沟球轴承SKF6205，它的故障是通过电火花加工的。诊断10种类型的故障类别为正常轴承、滚动体故障、外圈故障、内圈故障4类健康状况；每类健康状况(正常除外)包含损伤直径：0.007 inch,0.014 inch和0.021 inch，共计9种损伤状态。实验中，每类故障含有1000个样本，其中900个样本用于模型训练，100个样本用于模型测试，每个样本含有2048个数据点。其中，故障尺寸为0.014 inch的时域图如图4所示。

图4 信号4种状态的时域图

3.2 数据处理

从图4难以判断故障的类型，因此需对信号进行处理。首先，采用GSA优化VMD的参数，参数初始值如表1所示。粒子的初始分布与优化后粒子分布如图5所示。优化后的最优值为[K,α]=[5,1832]。

表1 GSA-VMD的参数

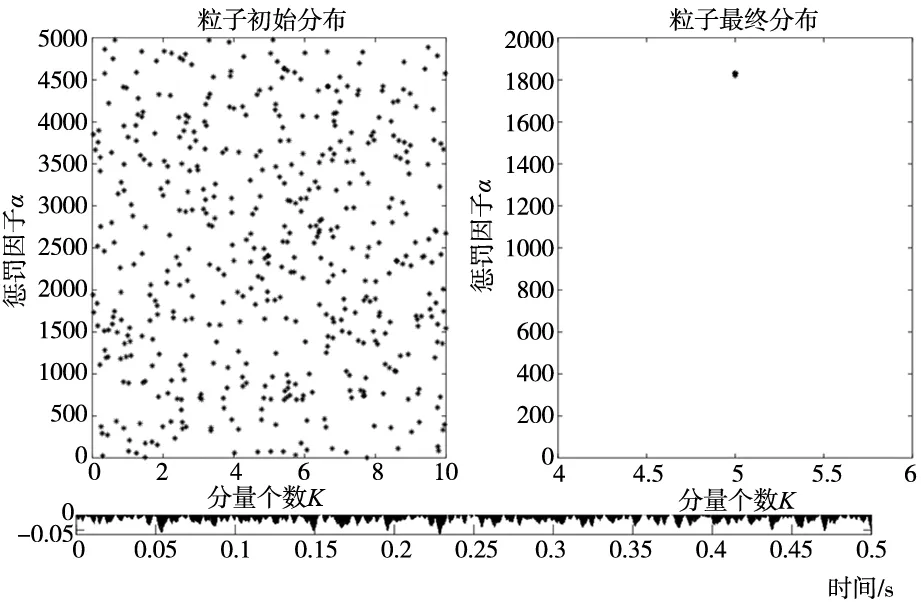
图5 粒子分布图

将最优值[K,α]=[5,1832]代入VMD中，依次分解轴承的故障信号。其中，对外圈故障信号进行分解后，模态分量如图6所示。接着，将每类故障信号和5个模态分量与原始振动信号联合构建样本集，作为PSO-CNN的输入，样本集的尺度为2048×6。

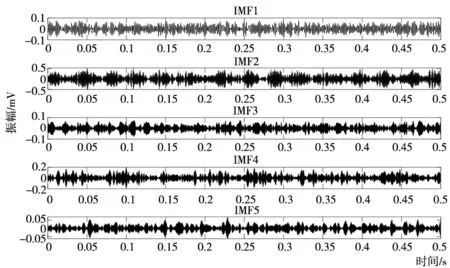
图6 外圈故障信号模态分量图

3.3 构建CNN诊断模型

首先，初始化自适应CNN模型的参数，有关参数如表2所示。在该模型中，池化层卷积核的大小为2，步幅为2；卷积核的步幅为1；激活函数为ReLU。然后，将归一化处理后的样本输入到自适应CNN模型中，得到的本实验CNN诊断模型如图7所示。

表2 自适应CNN模型的参数

图7 CNN诊断模型图

3.4 诊断结果与分析

为验证本方法的诊断性能，采用ANN、CNN-SVM[17]、WDCNN[11]、GA-CNN[18]4种方法进行对比实验。4种方法的结构如下：ANN结构通过经验和重复实验确定；CNN-SVM主要采用文献[17]的结构；WDCNN主要采用文献[11]的结构；GA-CNN主要采用文献[18]的结构。所提方法的结构通过PSO算法自适应地确定，具体参数如表3所示。5种实验方法的具体结构参数如表3所示。以模型WDCNN为例，In[2048×6]、16C[64×2]、16P[2×2]、FC[120]分别表示尺寸为 2048×6的输入、16个尺寸为64×2的卷积核、16个尺寸为2×2的池化核、神经元个数为120的全连接层。

表3 实验中模型的参数

图8为实验的诊断结果图。图中，横轴代表实验次数，纵轴表示每次实验的准确率。由图可知，在每次实验中，所提方法的分类准确率均高于95%。WDCNN方法的分类准确率大都低于为95%。ANN方法的分类准确率全低于为70%。CNN-SVM与GA-CNN方法的分类准确率都低于90%。综上所述，所提方法的诊断准确率与稳定性优于实验中的其他模型。

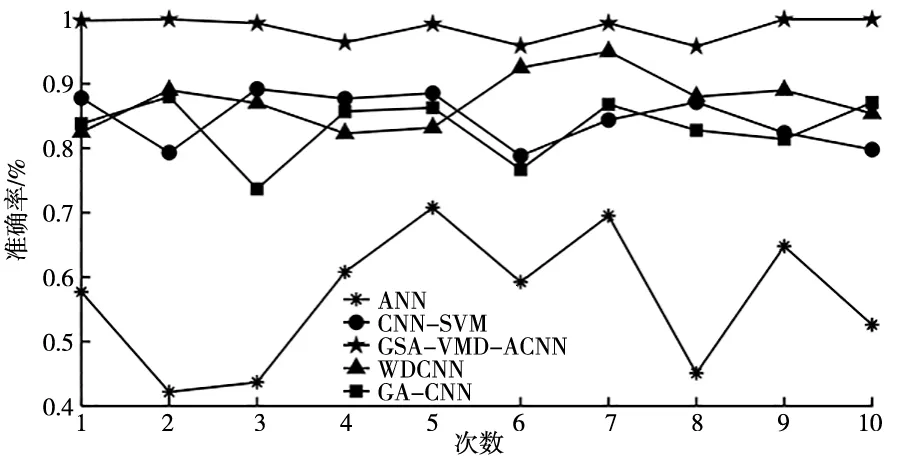
图8 诊断结果图

图9为所提方法的混淆矩阵，由图可知，所提方法在第三类故障样本识别中表现不佳，这可能是因为PSO的迭代次数少，搜寻的CNN架构不是最优的，导致未能搜寻到该类故障的本质特征。但是，所提方法在其他9类故障样本中识别的准确率均高于98%，并且所提方法仍能继续优化CNN架构，使诊断模型具有更优异的性能。

图9 所提方法的混淆矩阵

4 结论

本文研究一种基于GSA-VMD与自适应CNN的滚动轴承故障诊断方法。该方法采用GSA优化VMD的参数，然后利用PSO适应性寻优CNN的超参数，构建故障诊断模型。得到的结论如下：

(1)GSA能很好地优化VMD的参数，寻优出惩罚因子与分解数的最佳组合，实现振动信号的分解。

(2)PSO能自适应地寻优出CNN的6个超参数：CNN的层数、CNN层的类别、池化层的类型、卷积核的尺寸、卷积核的个数、全连接层神经元的个数，提高了构建基于CNN的轴承故障诊断模型的效率。