基于粒子群优化EKF的无传感器DPMSM滑模控制*

2022-07-27郑顺河孟克其劳海日罕

组合机床与自动化加工技术 2022年7期

郑顺河，孟克其劳,b,c，海日罕，王藤

(内蒙古工业大学a.能源与动力工程学院；b.风能太阳能利用技术教育部重点实验室；c.内蒙古自治区风电技术与检测工程技术研究中心，呼和浩特 010051)

0 引言

近年来，电机相关技术快速发展，使得直驱永磁同步电机(direct drive permanent magnet synchronous motor，D-PMSM)广泛应用于风力发电、飞轮储能、电动汽车等领域中[1]。在电机驱动系统中，直驱永磁同步电机需通过在电机轴上安装机械传感器来得到准确的转子位置和转速信号。但机械传感器不仅成本高，而且受限于恶劣的工业条件，因此无传感器控制技术成为近年来的研究热点[2]。常用的电机无传感器控制中，基于扩展卡尔曼滤波器(extended Kalman filter，EKF)的无传感器矢量控制系统具有收敛速度快、动态性能好、抗干扰能力强等优点[3]。

但是传统EKF需要反复试凑选取噪声协方差参数，往往费时且难以达到良好的效果，如果噪声协方差选取不当，EKF系统可能收敛过慢、抖动过大甚至完全发散。如何选取EKF的噪声协方差矩阵，研究者们也进行了不少尝试。

SHI等[4]通过试探法对噪声协方差矩阵进行选取，该方法易于使用，但耗时长、精度差且依赖于个人经验。佘致廷等[5]引入实数编码遗传算法对EKF的协方差矩阵进行优化，经优化后系统能够很好抑制噪声并且缩短了协方差矩阵的选取时间。但遗传算法不能利用网络反馈信息，搜索速度慢。WANG等[6]提出用蚁群算法对协方差矩阵参数进行优化，但蚁群算法中初始信息素匮乏，需要较长的搜索时间。

系统在受到外界扰动时，由于EKF算法具有延迟效应，转速变化会大于有传感器系统[7]，使得系统鲁棒性降低。而电机的转速控制器不仅需要精度高、动态响应快，还需对负载扰动和系统内部参数变化具有较强的鲁棒性，因此PI控制器难以达到系统控制要求。滑模控制(sliding mode control，SMC)与控制对象参数及扰动无关，具有快速响应、对参数变化及外部扰动不灵敏、鲁棒性强等优点，非常适合直驱永磁同步电机驱动系统的控制[8]。

赵峰、张宏达等[9-10]将滑模控制器引入转速控制中，滑模控制器能够对转速快速跟踪，鲁棒性强，但不可避免会引起系统抖振。相关学者为了削弱系统抖振，在滑模控制器的设计中采用趋近律的方法，在快速趋近滑模面的过程中对趋近速度加以控制，能够很好的削弱系统抖振现象[11]。戴鹏等[12]提出快速冥次趋近律设计滑模控制，使系统具有快速性和鲁棒性，但所选取的滑模面引入了微分状态量，求取速度微分时会引起高频噪声，降低控制器性能。

针对该问题，本文采用改进粒子群算法(improved particle swarm optimization，IPSO)对EKF的噪声协方差矩阵进行选取和优化。另外对传统指数趋近律进行了改进，用改进滑模控制器代替PI控制器，使系统获得更强的动态性能和鲁棒性。仿真验证表明经过改进后的控制系统，直驱永磁同步电机控制系统具有较高的转速控制能力和鲁棒性。

1 DPMSM的数学模型

为了避免在d-q坐标系中建模加重数学模型的非线性和增加递推计算时间，本文选择在α-β静止坐标系下构建电机非线性方程。表贴式DPMSM在α-β静止坐标系下的电流方程为：

(1)

机械运动方程为：

(2)

电磁转矩方程为：

(3)

式中，uα、uβ分别为α、β轴电压；iα、iβ分别为α、β轴电流；iq为旋转坐标系中q轴电流；R、LS、ψf、θe分别为电机的定子电阻值、定子电感、转子永磁体磁链、转子位置角；Te和TL分别为电磁转矩和负载转矩；D和J分别为阻尼系数和转动惯量；ωe和ωr分别为转子电角速度和机械角速度，其中ωe=pnωr(pn为电机极对数)。

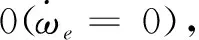
DPMSM在α-β静止坐标系中用于EKF状态估计的状态方程为：

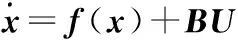
(4)

y=Cx

(5)

式中，x=[iα,iβ,ωe,θe]T；U=[uα,uβ]T；y=[iα,iβ]T。

根据系统的线性化理论，对f(x)进行线性化处理，可以得到对应的雅可比矩阵：

(6)

输入矩阵为：

(7)

输出矩阵为：

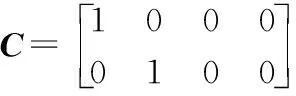
(8)

2 EKF转速与转子位置估算优化

2.1 扩展卡尔曼滤波器的设计

采用EKF算法，需对DPMSM的数学模型式(4)和式(5)进行线性化和离散化。假设采样周期为TS非常小，并加入系统噪声和测量噪声的影响，线性化和离散化的电机状态方程为：

xk=(I+FTS)xk-1+BTSUk-1+wk-1

(9)

yk=Cxk+vk

(10)

式中，I为单位矩阵；wk-1和vk分别是系统噪声和噪声，它们的均值为0且相互独立；协方差矩阵分别为Q和R，即Q=E[wwT]；R=E[vvT]。

将式(9)、式(10)代入EKF递推公式来实现对DPMSM转速、电流和转子位置角的估算。EKF估算的具体步骤如下：

(11)

求协方差矩阵预测，利用k-1时刻估计的误差协方差矩阵计算第k次的误差协方差矩阵的先验估计值Pk/k-1：

Pk/k-1=(I+FTS)Pk-1(I+FTS)T+Q

(12)

(2)计算卡尔曼增益：

Kk=Pk/k-1CT(CPk/k-1CT+R)-1

(13)

(14)

(4)更新最优估计误差：

Pk=(I-KkC)Pk/k-1

(15)

EKF算法经过以上4个步骤的迭代，就可以实现对DPMSM的转子速度和位置实时估计。需要注意的是扩展卡尔曼滤波器的设计虽然基于确定的数学模型，但模型在线性化和离散化的过程中存在着量化误差，同时系统对电压和电流的测量也存在测量误差，这些不确定性误差都被纳入到系统噪声和测量噪声中，因此系统噪声协方差矩阵Q和测量噪声协方差矩阵R的选取对EKF系统的收敛性和稳定性至关重要。

2.2 IPSO算法优化EKF噪声协方差矩阵

2.2.1 基本粒子群算法

PSO是模拟鸟群随机搜寻食物的捕食方式。算法通过群体中个体之间的协作与信息共享来寻找最优解。假设在一个D维的目标搜索空间，有N个粒子组成一个群落，粒子pi(i=1,2,…,N)的当前位置为Xi={Xi1,Xi2,…,Xid}，当前的飞行速度为Vi=(Vi1,Vi2,…,Vid)，pid为第i个粒子当前的搜索到的最优解，pgd为种群中所有粒子的最优解。在寻找这两个最优值时，粒子根据式(16)、式(17)来更新自己的速度和位置：

vid=ωvid+c1r1(pid-xid)+c2r2(pgd-xid)

(16)

xid=xid+vid

(17)

式中，ω为惯性权重；c1、c2为学习因子；r1和r2为[0，1]范围内的均匀随机数。

2.2.2 改进粒子群算法

在粒子群算法中，惯性权重ω是重要的参数，增大ω可以提高算法的全局搜索能力，减小ω可以提高算法的局部搜索能力。为避免算法容易早熟及后期容易在全局最优解附近产生振荡现象，本文采用线性递减权重法，其变化公式为：

(18)

式中，ωmax表示惯性权重最大值；ωmin表示惯性权重最小值；t表示当前迭代步数。

同时考虑到PSO算法受到随机因素影响较多，为了提高算法的适用性和收敛速度，采用混合策略，将自然选择机理与PSO算法相结合，其基本思想为在每次迭代中，根据粒子群适应度值将粒子群排序，用群体中最好的一半粒子替换最差的一半粒子，同时保留原来每个个体所记忆的历史最优值。

2.2.3 改进粒子群算法优化EKF协方差矩阵

噪声协方差优化就是在每个仿真周期对Q和R矩阵内的参数进行调整，每个粒子对应一组参数，对系统进行多次迭代，在每次迭代中计算系统仿真结果获得粒子的适应度值，根据适应度值得到个体最优位置和全局最优位置，迭代结束后获得全局最优粒子作为噪声协方差矩阵的参数。为了评价不同Q和R对EKF性能的影响，采用均方根误差(RMSE)为评价控制系统性能指标，适应度函数选为：

(19)

式中，si为实际转速；ωi为估计转速；n为采样次数，其值为仿真时间除以采样周期。

改进粒子群算法对EKF的参数进行优化，其流程图如图1所示。

图1 粒子群优化EKF过程示意图

2.2.4 改进粒子群算法收敛性分析

为验证上述方案合理性，采用PSO和改进粒子群算法对EKF进行优化，并比较优化结果。两种算法的相关参数设置如下：惯性权重ω=0.6，ωmax=0.9，ωmin=0.4；学习因子c1=c2=2；粒子数为20；最大迭代次数为40；空间维度为6(Q，R总共6个对角元素)；解空间[1e-10,200]。

图2 两种寻优策略收敛曲线

图2为两种算法适应度函数的收敛曲线，即系统性能指标RMSE的变化曲线。可见最优适应度值难以达到理想效果0，这是因为EKF具有延迟效应，在转速快速上升期间估计转速滞后于实际转速所导致。表1为两种寻优算法的性能比较。可见改进粒子群算法具有更强的搜索能力，能够提高寻优精度且保持较高的寻优速度。

表1 两种优化策略性能分析

3 滑模转速控制器设计

3.1 滑模控制器设计

(20)

由电机转速的状态方程可知，控制模型满足一阶单输入系统的切换函数设计。为消除系统稳态误差，将速度误差x1做积分运算，采用积分滑模面如下：

(21)

根据式(21)，对s进行求导有：

(22)

(23)

为提高系统动态性能和减弱滑模抖振，采用指数趋近律方法设计SMC转速控制器，指数趋近律的形式为：

(24)

式中，ε、k都是大于0的常数。

将式(20)与趋近律表达式建立等价关系，继而推导出控制器的数学模型：

(25)

在指数趋近律得到广泛引用的同时，有相关学者对指数趋近律进行改良。为进一步缩短趋近滑模面的时间，需要加快趋近速度；同时速度过快又会引起系统抖振，因此在快速趋近滑模面的同时还要减小到达滑模面的速度。在此基础上，引入改进趋近律：

(26)

式中，η、δ、ε、k均为大于0的常数。系统引入了指数项e-δ|s|，当|s|较大时，即系统状态距离滑模面较远时，指数项趋近于0，等速项εsgn(s)被放大，系统在εsgn(s)和ks作用下加速趋近滑模面。当|s|趋近于0，指数项趋近于一并且逐渐失效。η可调节分母近视为0的系统状态到达滑模面的距离。同时利用反正切函数值域的有界性，可以保证速度不会太大，引起系统抖振。

由于传统滑模控制器采用符号函数难免导致高频抖振。为了进一步削弱开关函数带来的系统抖振现象，本文将双曲正切函数代替传统的符号开关函数，双曲正切函数为tanh(s)：

(27)

由上述可得最终改进指数趋近律的控制器为：

(28)

3.2 稳定性证明

采用Lyapunov函数来对新型趋近律进行稳定性证明。Lyapunov函数如下：

(29)

(30)

3.3 改近指数趋近律特性分析

以经典系统为例对改进指数趋近律与传统指数趋近律进行验证分析。被控对象如下：

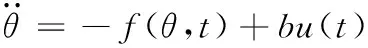
(31)

取滑模面：

(32)

求导得：

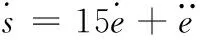
(33)

跟踪误差为：

(34)

式中，θd为给定的目标信号。

(35)

取改进指数趋近律有：

(36)

式中，ε=10；k=30；η=0.1；σ=20，取目标信号θd=sin(t)，被控对象初始状态为[-0.15 -0.15]，对两种趋近律进行仿真分析，仿真结果如图3～图5所示。

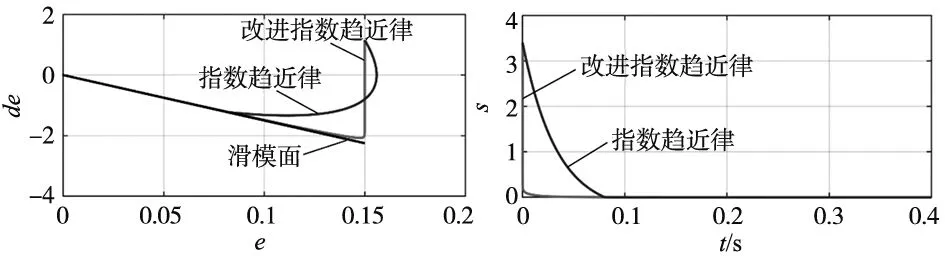
图3 滑模态相轨迹图4 趋近时间

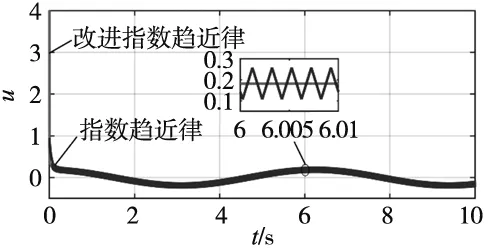
图5 控制器输出

结果表明，改进型指数趋近律可以减少趋近时间，快速趋近滑模面，并收敛于平衡点。同时由图5可见基于传统指数趋近律控制器输出抖振明显，而改进型趋近律控制器输出平滑，抖振得到有效削弱。

4 仿真与分析

为了验证优化方案的有效性和改进滑模转速控制器的正确性，本文利用MATLAB/Simulink搭建基于id=0的空间矢量控制的表贴式DPMSM系统仿真模型，系统原理框图如图6所示。

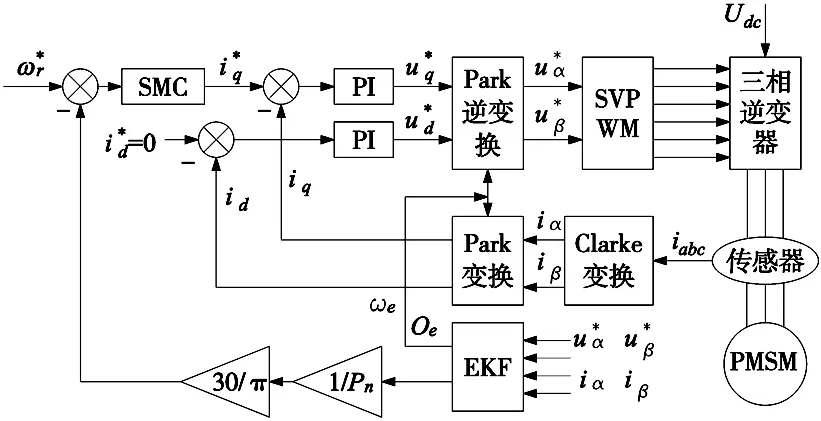
图6 系统原理框图

直驱永磁同步电机参数如下：定子电阻R=2.875 Ω，定子电感Ls=0.008 5 H，转子磁链ψf=0.3 Wb，转动惯量J=0.008 kg·m2，阻尼系数D=0；滑模控制器参数如下：η=5，δ=0.1，ε=0.01；EKF参数如下：x0=[0 0 0 0]，P0=diag([0.1 0.1 0 0])，试探法、PSO和IPSO优化的Q、R取值分别为：

试探法：

Q=diag([0.1,0.1,5,0.05]),R=diag([0.2,0.2])

PSO：

Q=diag([4.66706754922473,3.51407001728619,
50,18.5708126317066]),
R=diag([19.183267304730,29.196957738851])

IPSO：

Q=diag([15.7483240437961,12.5281571748522,
160.196984318041,1E-10]),
R=diag([128.336576027543,75.852734584808])

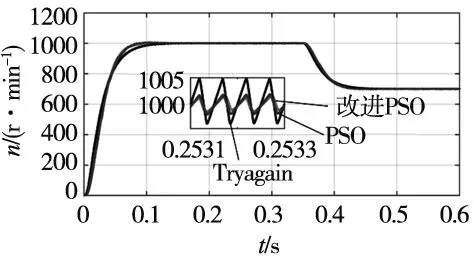
图7 EKF估计转速

为了验证IPSO优化EKF的有效性，给定电机转速1000 r/min，空载启动，0.35 s转速突变为700 r/min。图7为试凑法、PSO算法和IPSO算法得出的噪声协方差矩阵的估计转速图形，可以看出EKF估算能够对给定电机转速准确快速跟踪，且IPSO算法优化的系统可以更好地抑制噪声。

图8为EKF转子位置角估计值和实际值及误差波形。可见以式(20)为评价函数，通过PSO优化的系统在转子位置角的跟踪情况没有试探法好，而IPSO算法在系统稳定后转子位置角误差值保持在0左右，EKF的估算精度高。

(a) 电机实际转子位置和估算位置波形 (b) EKF估计转子位置与实际转子位置误差

图9为改进SMC、传统指数趋近律SMC和PI控制器转速之间的对比，图10为电机电磁转矩对比。

图9 电机转速图10 电机电磁转矩

由图可知基于改进SMC中电机转速在0.05 s左右达到设定转速，指数趋近律滑模控制需要到0.08 s，PI控制器需要0.1 s，在0.35 s电机突加负载TL=10 N·m，PI控制器与传统滑模控制器比改进SMC转速跌落大且回复慢。可见改进的SMC响应比传统的SMC和PI控制器要快，在突加负载时转速变化小，且很快恢复为原来状态，提高了系统抗负载扰动能力和鲁棒性。