基于Super-Twisting滑模观测器的永磁同步电机转速控制*

高 芮，宗学军，何 戡

(沈阳化工大学信息工程学院，沈阳 110142)

0 引言

永磁同步电机(permanent magnet synchronous motor,PMSM)具有转矩密度高、损耗小、精度高等优点，广泛应用于伺服、机器人和新能源汽车等领域。由于算法简单、可靠性较好，速度环采用PI控制器更为广泛；当出现参数变化、负载扰动等不确定性因素影响系统控制性能时，传统的PI控制难以满足高性能要求的应用场合[1]。为了解决PMSM内部参数摄动和外部负载扰动这些问题，许多先进的非线性控制方式应用到永磁同步电机中，如滑模控制、预测控制、自适应控制等[2-4]。其中，由于滑模控制(sliding mode control,SMC)速度响应快、鲁棒性强以及抗扰能力强等优势而被广泛应用。然而，抖振是滑模控制过程中不可避免的问题，不仅降低系统的跟踪精度和动态性能，严重时还会影响系统的稳定性。因此，解决抖振问题成为滑模控制方法的研究关键[4]。童克文等[5]采用一种变指数趋近律，减小转矩和磁链进入滑模面的脉动，增强了系统的鲁棒性；张晓光等[6]引用终端吸引子改变趋近律，但对系统参数要求较多。

在伺服系统中，通过观测器和滑模控制相结合的控制方式对扰动进行观测，可以进一步提高系统的抗扰性[7-9]。刘京等[10]利用滑模扰动观测器对外部干扰进行观测，并对速度控制器进行补偿，转速无明显超调；ZHANG等[11]基于扩展滑模扰动观测器对外部扰动进行观测并对观测值实施反馈补偿，通过开关系数增益实现了系统的稳定控制。

为了进一步降低抖振及提高系统的抗干扰性，本文采用新型趋近律滑模控制和三阶super-twisting滑模观测器(super-twisting sliding mode observer,STSMO)相结合的转速控制方式，保证系统的稳定性，同时能够提高系统的快速响应性和抗扰能力。仿真和实验验证了该控制方式的有效性和可行性。

1 永磁同步电机数学模型

永磁同步电机在d-q轴系下的电压方程：

(1)

磁链方程：

(2)

电磁转矩方程：

(3)

机械运动方程：

(4)

式中，R为定子电阻；ud、uq、id、iq、Ld、Lq分别为d-q轴下定子电压、电流和电感；ψd、ψq、ψf分别为d-q轴下定子磁链和永磁体磁链；ωe为电角速度；pn为极对数；ω为机械角速度；J为转动惯量；B为粘滞摩擦系数；Te为电磁转矩；TL为负载转矩；KT为转矩常数。

2 滑模控制器设计

2.1 新型趋近律

本文采用新型趋近律[10]：

(5)

式中，k>0；k1>0；δ>0；0<ε<1；0<α<2。

定义Lyapunov函数：

(6)

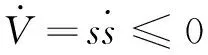
(7)

由于-c1≤0，所以

(8)

因此，新型趋近律满足滑模的可达性条件，系统在有限时间内可以收敛。

2.2 速度环滑模控制器设计

选取系统状态变量：

x=ωref-ω

(9)

式中，ωref为给定目标转速；ω为电机实际转速。

由于系统在趋近滑模面会出现抖振问题，积分滑模面[12]能够平衡转矩，抑制抖振，而且提高系统的鲁棒性。故选取积分滑模面为：

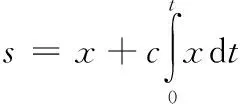
(10)

式中，c为滑模面的积分系数。

对式(10)求导，得到：

(11)

由式(4)可知：

(12)

定义扰动项为ζ(t)，式(12)可写为式(13)：

(13)

由式(5)、式(11)、式(13)可得到滑模控制律为：

(14)

由式(14)可以看到，扰动项ζ(t)对系统有较大的影响，而且是非线性变化，因此，需要设计观测器对ζ(t)的变化进行观测。

3 滑模观测器设计

在速度控制器的设计中，由于存在ζ(t)扰动。为了进一步提高系统的抗干扰能力，构造了三阶super-twisting滑模观测器的观测方法，用于估计控制器中的干扰。

3.1 三阶STSMO基本原理

定义观测系统的状态方程为：

(15)

式中，x1、x2为系统的状态变量；u为控制输入；ρ1(t)为扰动，且有界，满足|ρ1(t)|≤Δ。

为了观测式(15)中的状态变量，三阶STSMO可以用以下形式构造。

(16)

式中，k1、k2和k3为常数；带有符号“^”的变量代表相应的估计。

估计误差定义为：

(17)

因此，由式(15)、式(16)可以得到误差方程为：

(18)

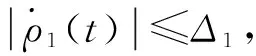
3.2 STSMO设计

对于速度控制器的输出，需要估计负载扰动TL。由于参数扰动是自然连续的，扰动的导数是有界的。根据动力学方程式，可得到ω与ζ(t)的状态方程为：

(19)

定义x1=ω，x2=-TL/J，x3=-ρ2/J，三阶STSMO可设计为：

(20)

为了在数字系统中实现所设计的三阶STSMO，对观测方程进行离散化为：

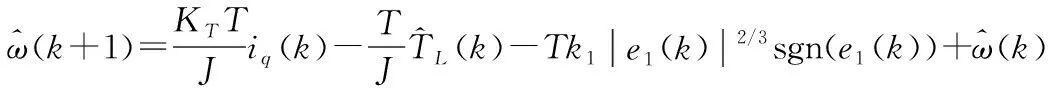
(21)

式中，T为采样周期。

三阶STSMO结构框图如图1所示。

图1 三阶STSMO结构框图

4 仿真与实验分析

4.1 仿真分析

为了验证本文采用滑模速度控制器与三阶super-twisting滑模观测器相结合控制方式的有效性，在MATLAB/Simulink环境下搭建永磁同步电机矢量控制调速系统进行仿真，选用基于TMS320F28335实验平台作为伺服驱动系统[14]。系统结构控制框图如图2所示。

图2 系统结构控制框图

永磁同步电机参数如表1所示。

表1 电机参数

PI控制器仿真参数：速度控制器的比例系数Kp=3，积分系数Ki=1；电流控制器d、q轴的参数相同，比例系数Kp=10，积分系数Ki=10。

滑模控制仿真参数：新型趋近律速度控制器：ε=0.1，δ=10，α=1.5，c=12，k=80，c1=100，c2=150；电流控制器Kp=10，Ki=10。三阶super-twisting滑模观测器：k1=8000，k2=100 000，k3=50。

图3 电机转速响应曲线

为验证本文所采用的基于新型趋近律滑模控制器的性能，采用id=0的PMSM矢量控制方法，与PI控制进行对比仿真。电流环均为PI控制器且参数不变。给定初始速度800 r/min时，电机在空载下启动，0.1 s时速度阶跃到1000 r/min，响应曲线如图3所示。可以看出：PI控制下转速的超调量约为60 r/min，而新型趋近律滑模控制下的超调量约为15 r/min；在转速变化时SMC的调节时间较短，而且能够快速地达到稳定状态。

图4 负载变化时速度响应曲线

为验证滑模观测器的有效性，对PI控制、新型滑模控制以及滑模控制器与三阶super-twisting滑模观测器相结合的控制方式进行对比仿真。电流环均为PI控制器且参数不变。给定初始速度800 r/min时，电机在空载下启动，0.5 s时系统加入负载转矩5 N·m，0.8 s时卸掉负载转矩5 N·m，负载变化时速度响应曲线与转矩响应曲线如图4和图5所示。

图5 负载变化时转矩响应曲线

可以看出，系统在突加负载或者突减负载时，PI控制的转速波动最大，波动值约为68 r/min，新型趋近律SMC的波动值约为33 r/min，而SMC与三阶super-twisting滑模观测器相结合(SMC+STSMO)的控制方式下转速波动最小，波动值约为8 r/min，且能较快的恢复到系统稳定状态。

图5从上至下分别为PI控制、SMC以及SMC+STSMO控制时，转矩随负载变化的仿真结果。可以看到：SMC+STSMO控制时，转矩响应最快且超调较小。

仿真数据结果表明，SMC+STSMO控制，具有较快的速度响应和转矩响应，而且抗干扰性较好。

4.2 实验分析

基于TMS320F28335控制板搭建PMSM调速实验平台进行对比实验。PMSM实验参数与表1参数相同。分别对PI控制和SMC进行实验验证，包括速度阶跃和突减负载时的动态响应两部分测试，实验结果图如图6、图7所示。

图6 速度阶跃变化时的动态响应

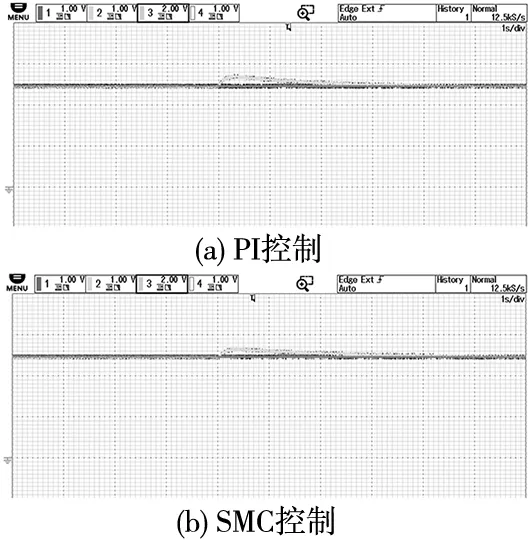
图7 突减负载时的动态响应

图6中，1通道为给定速度，2通道为实际速度，每格代表400 r/min。给定初始转速为500 r/min，1.5 s时速度阶跃到1000 r/min，3.5 s时速度阶跃到500 r/min。当速度发生阶跃时，PI控制时转速的调节时间为0.25 s，而SMC的调节时间缩短了40%，约为0.15 s，且无超调。

图7中，1通道为给定速度，2通道为实际速度，每格代表400 r/min。跟踪速度信号为1000 r/min，负载转矩为2.8 N·m下启动，4 s时负载突减到0 N·m。突减负载时，PI控制的转速波动较大，最大波动值约为80 r/min，而SMC的最大波动值约为40 r/min。

图8 PMSM转速响应曲线

对super-twisting滑模观测器观测值是否补偿到速度滑模控制器的输出端进行实验验证，实验结果如图8所示。图8中，1通道为实际速度，每格代表50 r/min。给定速度为50 r/min。

通过STSMO将观测到的负载扰动等效电流对速度滑模控制器进行补偿，相较于未补偿时转速平稳运行且波动较小，系统的转速控制性能明显改善。

实验结果表明，SMC+STSMO控制，提高了转速的动态响应性和系统的抗扰性。

5 结论

本文在PMSM调速系统中采用新型趋近律的滑模控制降低了系统的固有抖振，相比传统PI控制，速度变化时该控制方式的调节时间较短，实际转速能够快速地达到参考转速并稳定运行；当出现负载扰动时，采用三阶super-twisting滑模观测器对负载扰动进行观测，并将观测值补偿到速度控制器的输出端，电机能够平稳运行且转速波动较小，系统的抗扰性能明显改善。仿真和实验结果表明相比于SMC，本文所提的SMC+STSMO控制有效增强了系统的动态性和抗扰性，提高了系统的转速控制精度。