基于RAHEKF的主动配电网动态估计方法研究

2022-07-27蔡锦健王志平冯锡根

黑龙江电力 2022年3期

蔡锦健，王志平，冯锡根

(1. 东莞理工学院电子工程与智能化学院，广东东莞 523808；2. 广东工业大学自动化学院，广州 510006；3. 江门市电力工程输变电有限公司，广东江门 529030)

0 引言

随着大规模分布式电源和电动汽车接入电网，更多不确定性因素将影响电力系统的正常运行，给主动配电网的运行方式、态势感知和量测配置等带来更多新的挑战[1]。为了能够更好地感知电网运行状态，有必要加强对电网的实时监测和控制，相量量测装置(phasor measurement unit，PMU)的配置为电力系统动态估计提供了基础，基于实时准确的量测数据，可以及时反映配电网的动态特性。

动态状态估计主要以扩展卡尔曼滤波方法为主，但由于其需要准确获取模型参数，系统和量测噪声的特性需要提前确定，EKF才能得到理想的结果。同时在需要计算雅可比矩阵的过程中，存在线性化误差。经过多次对EKF进行改进，先后提出无迹卡尔曼滤波算法[2-4]和容积卡尔曼滤波算法[5-8]等方法，有效提高了滤波的精度，但计算复杂度和计算时间都有所增加。

针对EKF线性化带来的误差，导致估计精度下降问题，文献[9]提出了一种改进扩展卡尔曼滤波方法，利用不确定项表示线性化误差，在保证精度的基础上提升了计算速度。文献[10]在扩展卡尔曼滤波将泰勒展开保留到二阶项，来降低线性化带来的误差，增强算法在系统突变下的预测能力。对于模型不确定性引起估计精度不足问题，文献[11]提出了一种基于自适应扩展卡尔曼滤波(adaptive H∞ extended kalman filter，AHEKF)的方法，对发电机进行动态估计，算例结果表明该方法优于EKF，且有较高的鲁棒性。

在系统观测数据较少的低压配电网，文献[12]将增益矩阵和雅可比矩阵设为常数矩阵，较大干扰时才修改，来提高状态估计的实时性，通过实际的现场测量数据来验证所提出算法的性能，在计算速度和准确性上优于经典方法。

为了提高EKF的抗差性，在考虑粗差的情况下，文献[13]提出一种基于抗差扩展卡尔曼的估计方法，分别在较大外部干扰和估算误差时，验证其抗粗差的性能，让系统能够很好的收敛。文献[14]采用最小绝对值实现抗差状态估计，实现对不良数据的检测和辨识。

现有的状态估计模型一般会先假设系统和量测噪声是服从高斯分布的白噪声[9]，基于此假设下进行动态估计的预测和分析。在实际的电力系统中，噪声并不一定是高斯白噪声，还存在着量测误差，给系统增加不确定性，使估计结果的准确性难以保证。针对EKF的系统和量测噪声问题，文献[15]提出了一种基于时变噪声的改进扩展卡尔曼滤波算法，使系统正常情况和异常情况下的滤波精度能在允许的范围内。针对模型不确定和噪声不确定问题，基于鲁棒控制理论，文献[16]提出了一种自适应扩展卡尔曼滤波器进行电力系统状态估计和处理模型的不确定性，通过大量的实验算例，验证了该方法的有效性和鲁棒性。

综上所述，系统和量测噪声、EKF线性化带来的误差以及不良数据对状态估计结果造成极大的影响。针对主动配电网运行中存在的拓扑结构变化、负荷波动和分布式电源出力波动等问题，文中提出了鲁棒自适应H∞扩展卡尔曼滤波算法进行动态估计，能有效地降低噪声和不良数据的影响，实现对主动配电网高效准确的动态估计。首先，对于不良数据，采用量测不确定性理论，引入测点评价函数，来克服不良数据引起的问题。其次，对于线性化误差，将EKF量测函数的泰勒展开保留到二阶项，来降低线性化带来的误差，增强算法在系统突变下的预测能力。最后，对于噪声不确定问题，采用渐消记忆时变噪声，来模拟噪声的变化，增强算法对噪声动态变化的鲁棒性。在改进的IEEE 33节点系统分别对不良数据、系统负荷突变和分布式电源功率连续大范围波动的情景下，比较EKF和AHEKF，对比它们之间的精确性和鲁棒性。

1 主动配电网动态估计模型

为了能够准确地感知和识别电力系统的运行态势，选取节点电压幅值和相角作为状态变量，选取第一个节点为参考节点。对于n个节点的系统，在k时刻，状态变量可以表示为

xk=[V2,k,V3,k,…,Vn,k,θ2,k,θ3,k,…θn,k]T

(1)

量测数据可以通过数据采集与监视控制系统(supervisory control and data acquisition, SCADA)和PMU量测系统读取。在主动配电网中，量测量还包括可再生能源输出有功和无功的功率等。结合实时量测数据与伪量测量，伪量测的生成方法可以参考文献[17]，那么主动配电网的量测量表示为

zk=[Pi,k,Qi,k,Pij,k,Qij,k,Vi,k,θi,k]T

(2)

式中：Pi,k和Qi,k为k时刻节点i的注入有功功率和无功功率；Pij,k和Qij,k为k时刻支路ij的有功功率和无功功率；Vi,k和θi,k为k时刻节点i电压的幅值和相角。

以节点电压幅值和相角作为状态变量，那么它与量测量的关系可以表示为

(3)

(4)

(5)

(6)

式中：Vi、θi分别表示节点i的电压幅值、相角；Gij、Bij为支路电导、电纳；Gs,i、Bs,i为节点i的自电导、自电纳。

在连续时刻下，非线性系统状态转移方程和量测方程可以表示为

xk=f(xk-1)+ωk-1

(7)

zk=h(xk)+vk

(8)

式中：xk和xk-1分别为k时刻、k-1时刻的状态变量；zk为k时刻系统的量测量；f(·)为相连时刻状态变量间的转移函数；h(·)为量测函数；ωk-1为k-1时刻的系统噪声，满足的协方差矩阵为Qk-1；vk为k时刻的量测噪声，满足的协方差矩阵为Rk。一般会假设噪声为服从高斯分布的白噪声，即系统噪声ωk-1～N(0,Qk-1)和量测噪声vk～N(0,Rk)。

状态转移方程采用Holt两指数平滑法[18]表示，f(xk)可以表示为

f(xk)=ak+bk

(9)

(10)

bk=β(ak-ak-1)+(1-β)bk+1

(11)

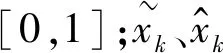
2 基于RAHEKF的动态估计

在实际电网中，SCADA和PMU在量测和传输过程中，不可避免地会出现不良数据。针对这样现状，基于AHEKF的状态估计的结果不如理想，因此该文在提高算法抗差性的基础上，提出了一种鲁棒自适应H∞扩展卡尔曼滤波方法。

2.1 计算精度

(20)

(21)

(22)

采用最小二乘法，最小化目标函数为

J(x)=(z-h(x))TR-1(z-h(x))+

(23)

把目标函数对状态变量求偏导并令之为零，可得极值条件为

(24)

则有

(25)

(26)

式中：K为滤波增益矩阵。

2.2 算法鲁棒性

在提高算法的鲁棒性上，该文基于量测不确定性理论，引入测点评价函数。对于某一测点，定义测点在状态变量x下的相对偏差为

(27)

式中：Ui为在置信水平p对应的测点的不确定度，与量测装置的精度有关。

若测点i在状态变量x下的相对偏差|di|≤1，判定该测点为正常测点，若|di|>1，那么该测点为异常测点。

根据上述特点，参考正常测点的定义，搭建测点评价函数[5]，用来判断测点是否为正常测点:

(28)

式中：λ和k为曲线拟合系数，通过测试法来确定参数λ和k的数值，一般取λ=1～5，k=2～4。

(29)

2.3 RAHEKF算法流程

RAHEKF算法流程为(见图1)：

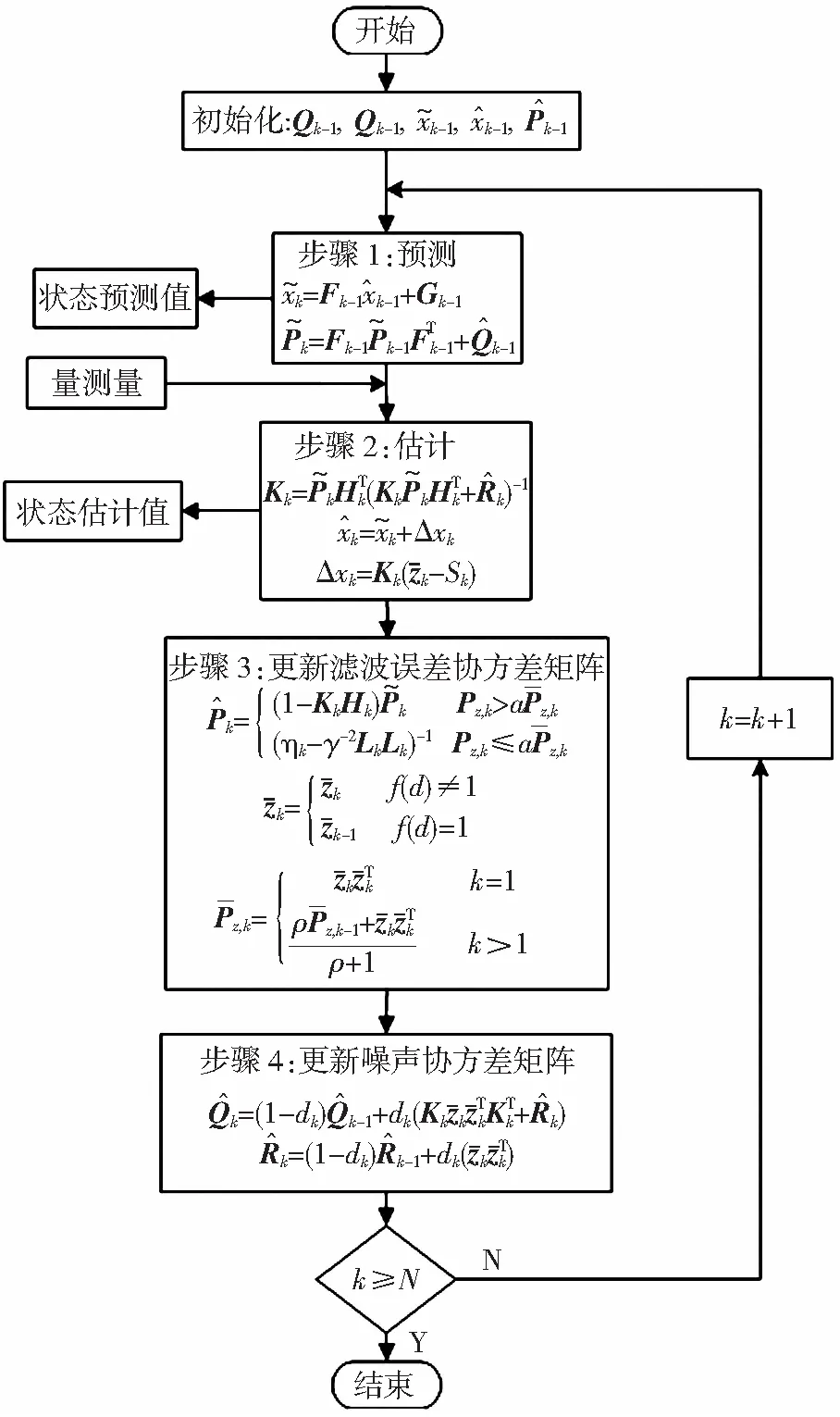
图1 基于RAHEKF的动态估计流程图Fig.1 Flow chart of dynamic estimation based on RAHEKF

1)预测：

(30)

(31)

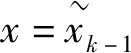
2)估计:

(32)

(33)

(34)

3) 滤波误差协方差阵更新。基于准则设计的更新方法：

(35)

(36)

(37)

(38)

(39)

4) 噪声协方差矩阵更新:

(40)

(41)

(42)

(43)

式中：b为遗忘因子，b∈[0.95,0.995]。

3 实验结果与分析

为了检验该文方法的可行性和有效性，基于Mtalab 2019 b环境下编制测试程序，以改进的IEEE 33节点系统进行了分析。针对主动配电网运行中存在的拓扑结构变化、负荷波动和分布式电源出力波动等问题进行实验探讨。

在IEEE 33节点系统的基础上，在节点13和节点30上分别接入光伏发电系统和风力发电机组，从而形成主动配电网，系统线路如图2所示。风力发电机的额定容量为100 kW，光伏发电系统的额定容量为50 kW，设备参数参考文献[19]。夏季典型日下风机和光伏的出力系数参考文献[20]。

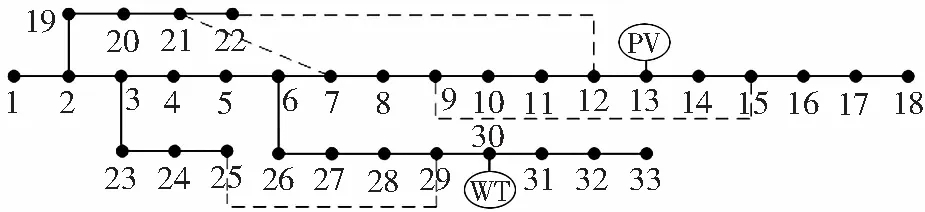
图2 改进的IEEE 33节点拓扑图Fig.2 Improved IEEE 33 node topology diagram

在夏季典型日，每隔15 min取采样点数据的均值，得到负荷曲线并进行归一化处理后，模拟仿真动态潮流[15]，日负荷曲线如图3所示。

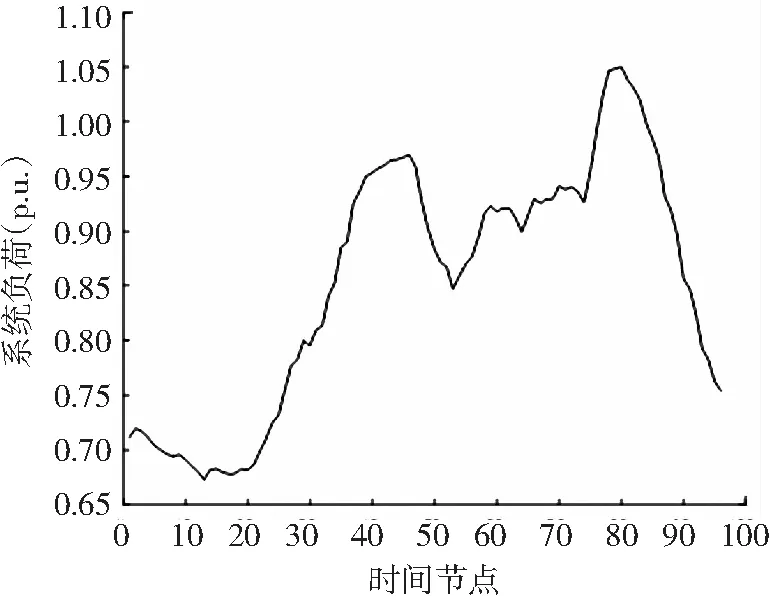
图3 夏季典型日下负荷系数变化图Fig.3 Variation of load factor during typical day in summer

该文对改进的IEEE 33节点系统进行模拟仿真，取基准功率为10 MVA，基准电压为12.66 kV。计算统一采用标幺值。以潮流计算的结果作为真值。选取162个量测量，在潮流计算结果上施加2%高斯噪声，来作为量测数据。

为了能够准确地比较状态估计结果的优劣，定义相对偏差指标作为算法性能比较的指标，电压幅值和相角的相对偏差指标EV和Eθ定义为[21]

(44)

(45)

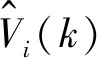
3.1 正常情况

基于改进的IEEE 33节点系统作为主动配电网，分别采用EKF、AHEKF和RAHEKF进行动态仿真测试，选取节点6和30作为观测节点，比较3种算法下的状态估计值结果，如图4和图5所示。

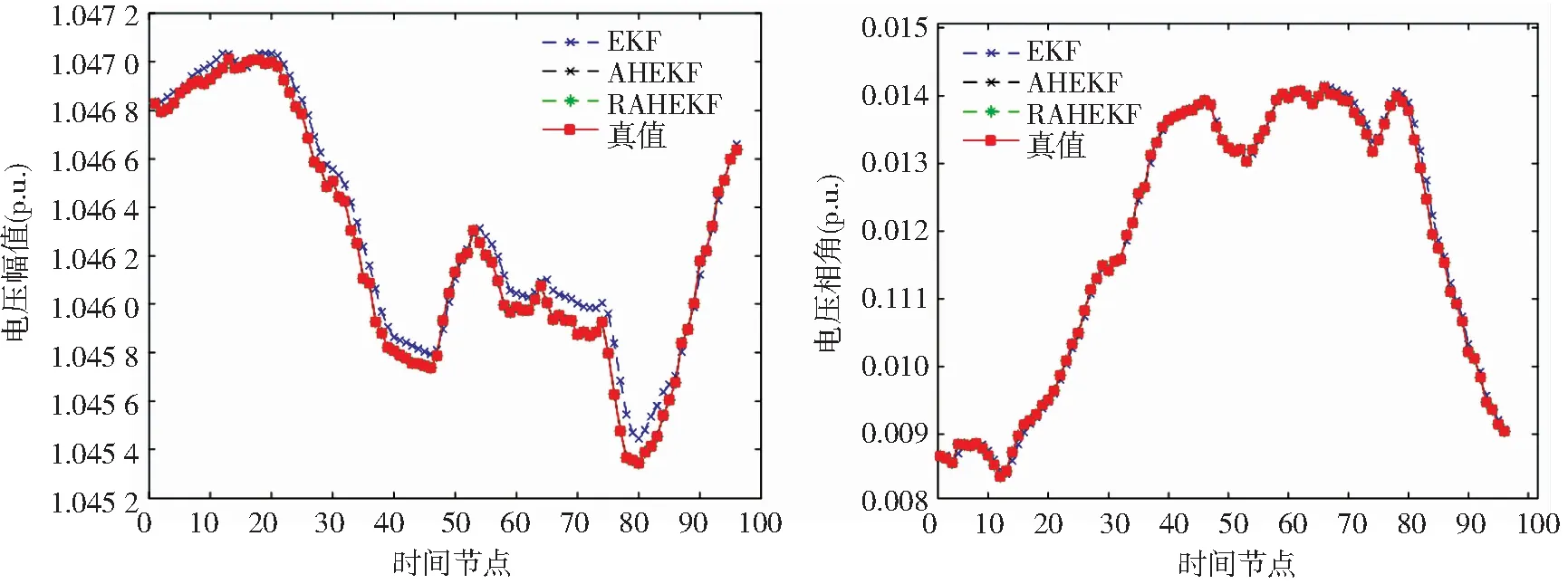
图4 节点6各时刻电压幅值和相角的估计值与真值比较图Fig.4 Comparison of estimated and true values of voltage amplitude and phase angle at node 6

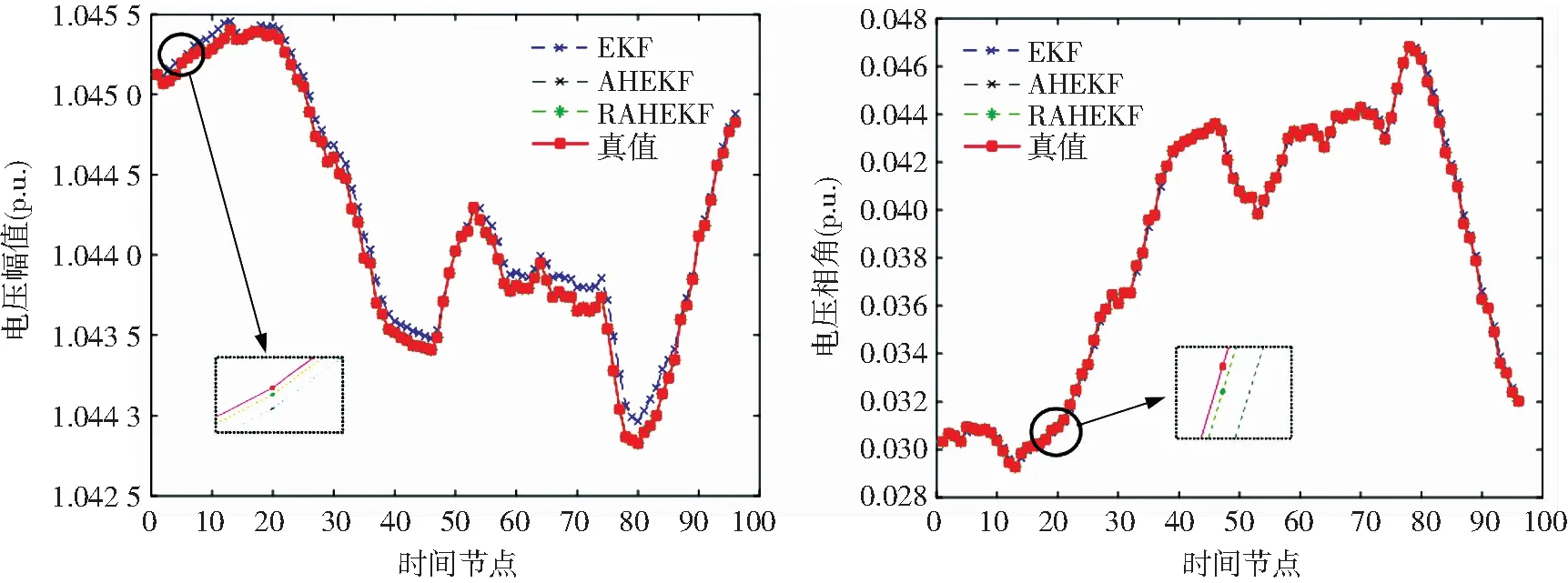
图5 节点30各时刻电压幅值和相角的估计值与真值比较图Fig.5 Comparison of estimated and true values of voltage amplitude and phase angle at node 30

图4和图5表明了在96个连续采样的时刻内，节点6和节点30的电压幅值和相角的动态变化图。由图4和5可知，基于EKF的电压估计值与真值偏差较大，其他2种方法的估计值与真值基本重合。显然，EKF的估计效果明显不足于其他2种方法。正常情况下，AHEKF和RAHEKF的状态估计效果较好，表明了采用渐消记忆时变噪声，来模拟噪声的变化，能够有效增强算法对噪声动态变化的鲁棒性，有助于提高算法的估计精度。

为了能够更加直观地比较AHEKF和RAHEKF估计能力，通过比较电压的真值与估计值之间的误差，来分析AHEKF和RAHEKF的估计精度。通过电压各个时刻真值与估计值的误差绝对值，来表征状态估计的精度。节点6和节点30各时刻电压幅值和相角的误差如图6和图7所示。

图6和图7表示了分别基于AHEKF和RAHEKF算法进行动态估计，节点6和节点30在各个时刻求解的估计值与真值之间的误差的绝对值分布。很显然，RAHEKF的电压幅值和相角的偏差绝大部分是少于AHEKF的。由于将量测函数的泰勒展开保留到二阶项，来降低线性化带来的误差，增强算法在系统突变下的预测能力，RAHEKF的估计精度有所提高。系统正常运行条件下，RAHEKF能够准确有效地估计各节点的电压幅值和相角，估计值与真值的误差明显少于其他2种估计方法，具有更高精度。因此，在正常情况下，RAHEKF具有更优的动态估计能力，估计精度更高。

图6 节点6各时刻电压幅值和相角的差值比较图Fig.6 Comparison of the difference between the voltage amplitude and the phase angle at node 6

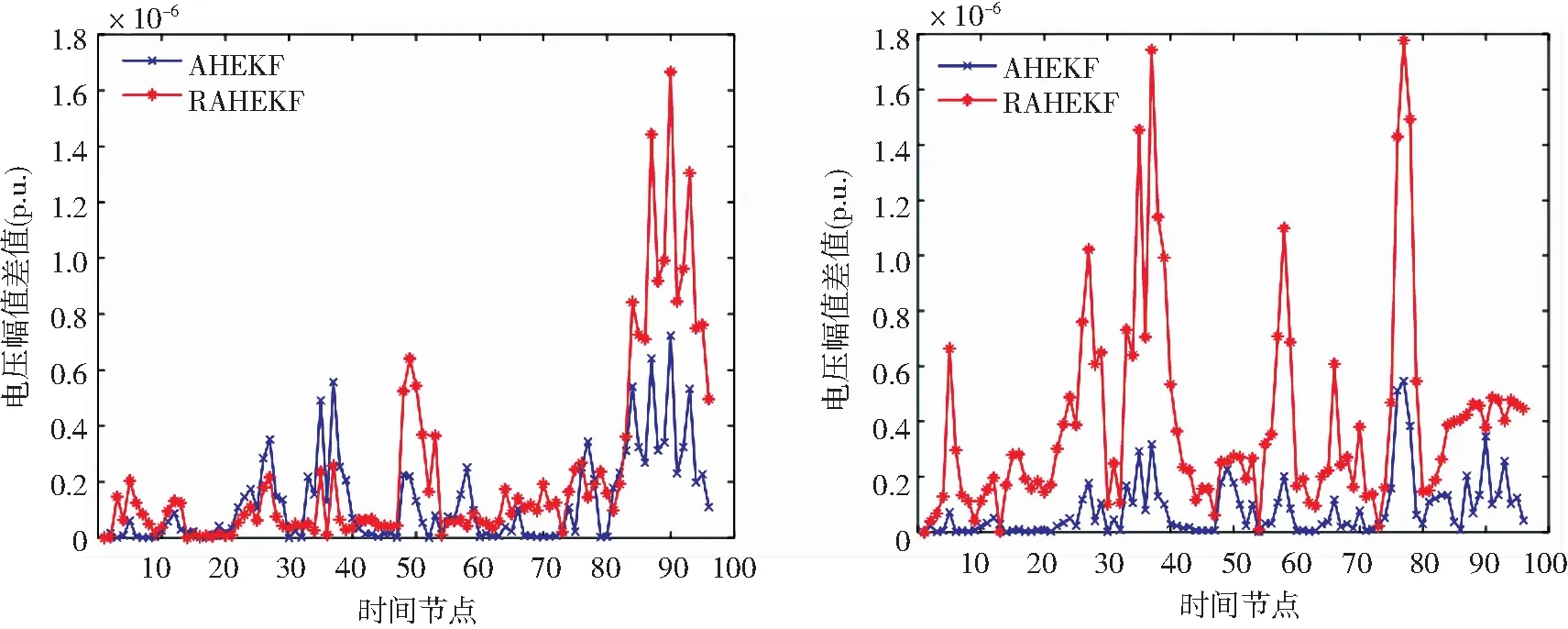
图7 节点30各时刻电压幅值和相角的差值比较图Fig.7 Comparison of the difference between the voltage amplitude and the phase angle at node 30

此外，在正常运行条件下，主动配电网的拓扑结构也会发生变化，以使配电网达到更优的经济运行。因此，假设某一时段k=77～83时，改进的IEEE 33节点系统的拓扑结构发生变化，线路的分段开关9—10和14—15断开，分段开关9—15和12—22闭合后，采用RAHEKF进行动态状态估计，选择节点9作为观测节点，状态估计结果如图8所示。在图8中可以发现，当主动配电网拓扑结构发生变化时，基于RAHEKF方法的估计值也会随之变化，能够有效地估计出变化后各节点的电压和相角，能够适应主动配电网灵活的运行场景。

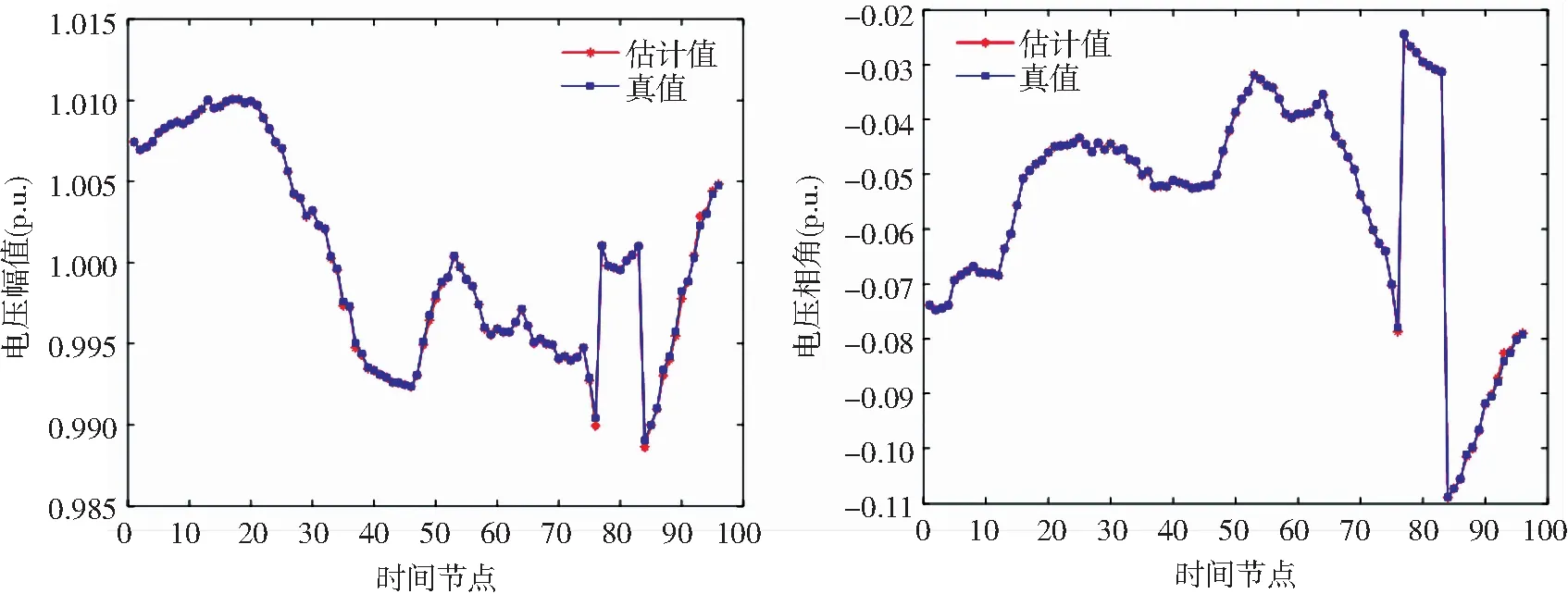
图8 节点9各时刻电压幅值和相角Fig.8 The voltage amplitude and the phase angle at node 9

3.2 抗差性测试

在改进的IEEE 33节点系统进行动态状态估计，测量不确定度Ui=3σi，k=1.3，λ=1.333 3。一般情况下，量测误差大于3σi被认定为不良数据。坏数据通过对量测数据加减50%、置零或者改变符号等方式获取。假设某一时刻，出现不同比例的坏数据，分别用所提的3种方法进行仿真测试。对比结果如表1所示。由于基于PMU和SCADA的配电网动态状态估计，PMU可以提供高精度的量测数据，因此该文假设量测数据中出现坏数据的比例较少。

由表1可知，在不同比例坏数据下，基于EKF的状态估计结果比其他2种方法明显不足。在理想情况下，量测数据中未出现坏数据，RAHEKF的状态估计结果比AHEKF的准确性更高，具有更好的估计能力。

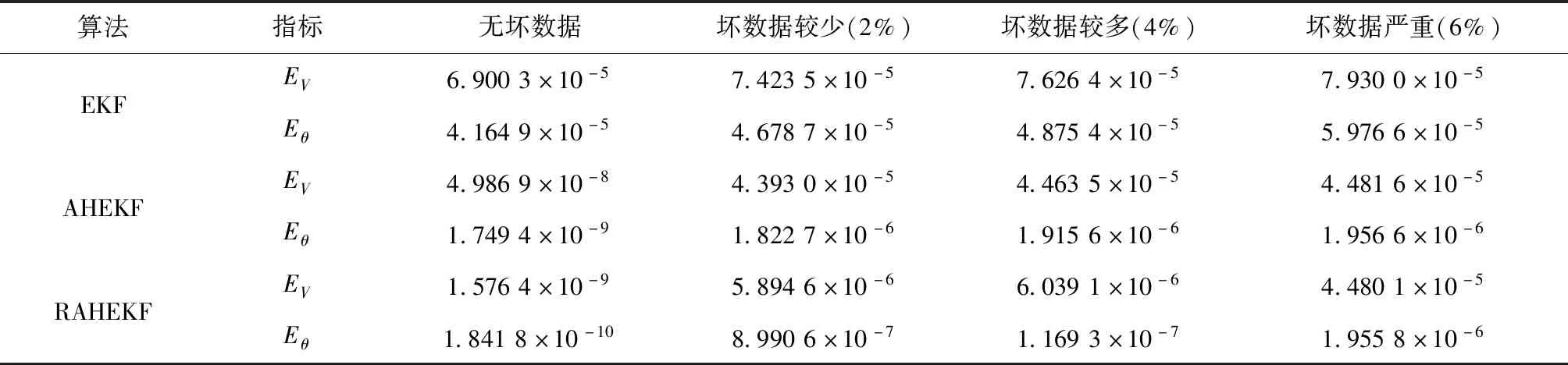
表1 3种算法下的状态估计准确性比较Table 1 State accuracy comparison under 3 scenarios

当量测数据中出现较少坏数据时，3种方法的估计精度均有所下降，而RAHEKF和AHEKF下降的幅度明显，但估计精度仍比EKF高。由于RAHEKF和AHEKF均采用渐消记忆时变噪声，坏数据对噪声动态变化产生不良影响，从而导致其精度的下降。而RAHEKF引入了测点评价函数，能够有效识别不良数据，降低其对渐消记忆时变噪声的鲁棒性，从而保证状态估计结果具有较高的精度。针对PMU配置下，坏数据比例较少，显然，RAHEKF具有更高的估计精度和更强的鲁棒性，能够有效应对实际情景中不良数据的影响。在坏数据较多的情景下，估计精度进一步下降，RAHEKF仍有较高的估计精度。

随着坏数据比例提高，状态估计结果准确性均有所下降，特别是在坏数据严重的时候，3种方法的估计精度都明显下降。在出现较多坏数据时，应该先进行不良数据的监测与辨识，降低不良数据在量测数据中的比例，再进行配电网的动态状态估计，但相对来说，坏数据对RAHEKF的状态估计结果的影响相对较少。

当系统中出现不同比例的坏数据时，RAHEKF能够降低其对状态估计的影响。在坏数据较少的情况下，能够实现更好精度的估计，可以与基于PMU动态估计更好地结合，实现高效精确的动态估计。

3.3 负荷突变测试

主动配电网在运行的过程中，某一时刻节点负荷量大，如电动汽车的无序接入，导致配电网负荷短时间内大幅度增加。以改进的IEEE 33节点动态仿真系统，假设时段k=10～12，节点6的负荷由0.004 6 (p.u.)突变到0.092 (p.u.)。节点6电压幅值和相角的变化如图9和图10所示。

图9和图10分别给出了节点6在系统发生突变时电压幅值、相角的真值以及3种算法的状态估计值。当系统负荷发生突变时，RAHEKF的状态估计值更加接近真值，能够更好地反映系统的动态变化情况。显然，RAHEKF能够更好地适应系统发生负荷突变的情况，对配电网实现更加准确的状态估计。

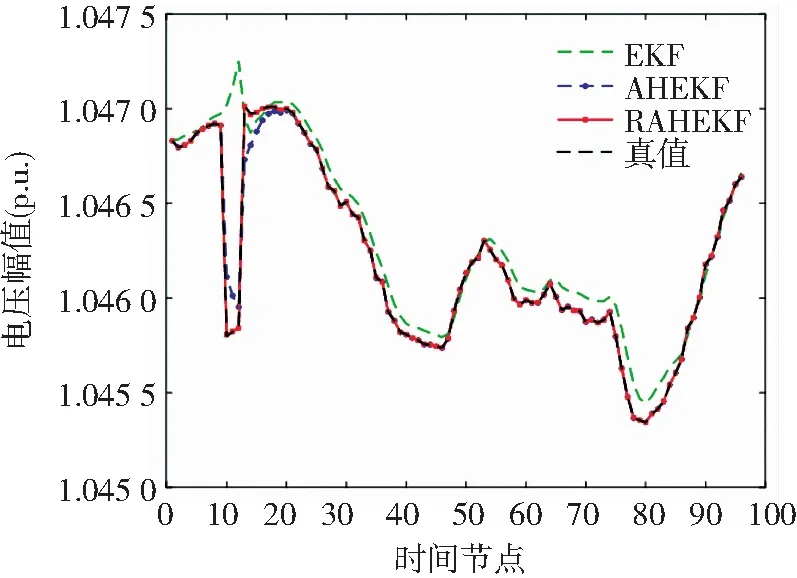
图9 节点6在各时刻的电压幅值Fig.9 The voltage amplitude at node 6

图10 节点6在各时刻的电压相角Fig.10 Voltage phase angle atnode 6

主动配电网会接入各式的分布式电源，而分布式电源的出力是动态变化的，导致分布式电源接入节点电压的变化，从而影响主动配电网的正常运行。因此对分布式电源接入节点进行有效的估计也显得尤为重要。以改进的IEEE 33节点动态仿真系统，设定时段k=40～43，风力发电机组的输出功率发生大范围波动，模拟日常阵风给风机运行造成的影响，假设该时段节点30接入风机的输出功率为0.01、0.04、0.01和0.02 ，在k=35～45时刻来观测节点30电压幅值和相角的变化，如图11所示。

由图11可知，在风机输出功率连续大范围出现波动时，RAHEKF能够有效地对接入节点进行精确的动态估计，估计值与真值基本重合。当风机功率连续较大变化时，RAHEKF估计效果比EKF和AHEKF更具有优势，具有更好的估计效果，能在接入分布式电源的主动配电网中得到有效的应用。

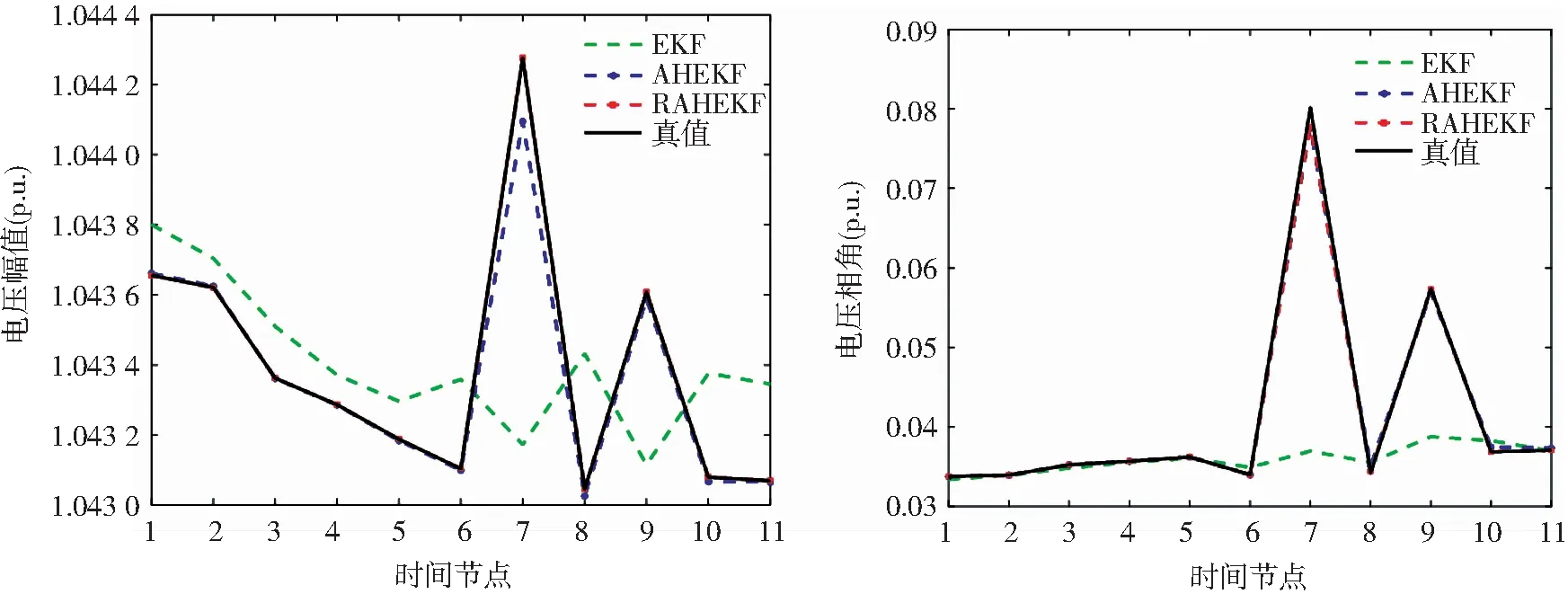
图11 节点30在时刻35到45之间电压幅值和相角的估计值与真值比较图Fig.11 Comparison of estimated and true values of voltage amplitude and phase angle of node 30 between time 35 and 45

3.4 算法性能分析

在改进的IEEE 33节点系统仿真测试中，RAHEKF算法相比较于AHEKF算法滤波精度更高，状态跟踪能力更强。在有不同比例的不良数据下，RAHEKF算法具有更好的抗差性以及更优的滤波性能。在对系统96次采样中，RAHEKF的动态仿真时长为1.979 0 s，AHEKF的动态仿真时长为1.204 0 s。那么每次采样后，RAHEKF平均单步计算时长为0.02 s，而AHEKF为0.013 s，因此基于RAHEKF状态估计时长比AHEKF有所增加。但是PMU每次采样间隔的时间为0.05 s，在估计时长稍有增加的情况下仍满足实际工程应用的需求。