基于多层植被水流实验的流速及应力的分布解析解研究
2022-07-27侯雨坤
罗 健,耿 川,侯雨坤
(中交第二航务工程勘察设计院有限公司,武汉 430060)
0 前 言
近年来,为贯彻“绿水青山就是金山银山”理念,国家大力开展河湖水环境综合治理工程。随着水生态修复以及海绵城市工程在国内的开展,河道修复中栽种挺水植物、沉水植物等措施普遍运用,使工程后的河底从原有的“光面”逐渐转化为成为多层植被的形态,也明显影响了河湖水动力特征。在这样的背景下,研究多层植被背景下的水动力变化情况对分析河流流态、确定防洪高程、准确分析污染物迁移等工作具有重要研究意义。
国内对植被水流的研究起步较晚。自2000年起,我国对植被水流的研究主要分为4个方面:
第一,植被水流的基础理论研究,即通过数学模型等理论研究推导得出植被水流的特性。有些学者试图将植被水流进行分类并分别进行研究[1-4];有些则对单一植株或均匀分布植株对水流的影响进行理论分析[5,6]。
第二,植被水流的实验研究,即在实验室中对自然状态下的植被水流进行经过一定条件简化(如植被直径均一化,分布规律化)后的实验。有些学者通过实验结果找出了植被水流的规律[7-10];有些学者则从实验结果反推基本理论[11-14]。
第三,植被水流的数值模拟,有些学者根据植被水流的复杂性,加入植被阻力项或对纯水模型进行修改,从而建立了自己的数值模拟模型[15-18];有些则分析了现有数学模型的适用范围或指出了已有模型的不足[19-21]。
第四,将基本理论与实际环境问题相结合,有些学者针对特定湿地区域的水环境问题展开研究,并提出相应的解决对策[22-24];有些学者从基本理论层面分析植被对水流环境的影响[25-34]。有些学者利用成熟的水流数值模拟软件进行植被水流的计算,为具体工程问题服务[35,36];有些学者总结了某一类工程实际问题中常遇到的植被水流问题,并对其展开研究[37-41]。
植被并非是以等高且均匀的方式分布在河道中的,而是往往由不等高的不同种类的植被构成,且呈不均匀分布的状态,而这些不均匀分布的植被对水流所起的作用与单层均匀分布的植被有着极大的不同。为此,以双层水流作为研究对象,通过对淹没及非淹没植被水流进行实验,探究了双层植被水流在不同的水深区间的不同特性,并对双层植被水流进行了分层,分析得出每层水流控制性方程的解析解,为更加深入的了解多层植被水流的水力特性提供重要参考。
1 研究方法
本研究选择在20 m长的水槽中进行双层植被水流实验,水槽宽度为1 m,高度为0.5 m。经分析,曼宁糙率系数为约0.09~0.15,并以此为依据计算均匀流水深,调节水槽尾部的尾门以使水流达到均匀流状态,并通过测量上下游水深来确保水流处于均匀流状态。水槽设计底坡S0为0.4‰。上下两排长度不同的钢钉被用来模拟刚性植被,上层植被高度h1=0.24 cm,下层植被高度h2=0.135 cm。流速使用Micro ADV 进行测量。钢钉的具体分布如图1所示。
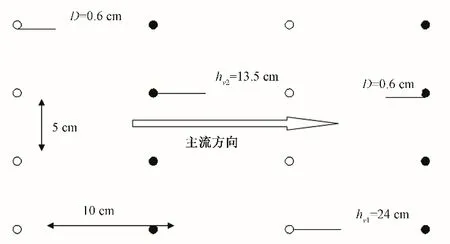
图1 双层植被分布示意图Fig.1 A schematic map of double layer vegetation distribution
为明确展示紧邻刚性、柔性植被的位置,并探寻与植被有一定距离,不受植被干扰的位置,流速及切应力吹响分布的规律。本研究将紧邻植被的测线与不受植被干扰的测线分为了B1、B2 两组,本次实验共测量了四组不同工况下的双层植被水流,具体工况如表1所示。

表1 双层植被水流实验工况的相关数据Tab.1 The related data of the experimental conditions of the two-layer vegetation flow
本次实验共测量了10 条不同位置的垂线上的时均流速分布,这10条垂线的位置如图2所示。
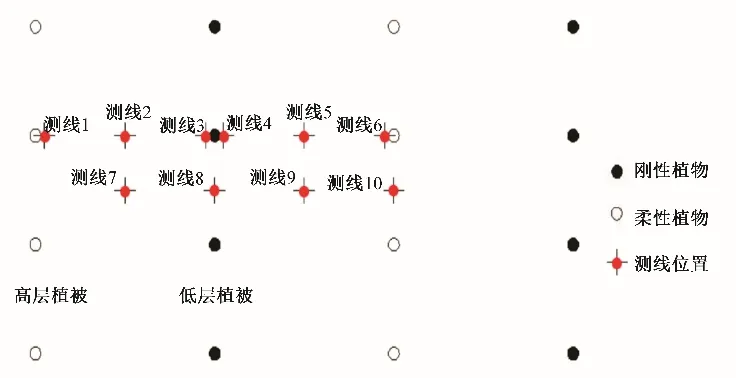
图2 测线位置布置图Fig.2 Layout of line position
实验测得的垂向流速分布数据如图3所示,可以看出,淹没和非淹没状态的双层植被水流垂向流速分布在不同的水深区间具有明显不同的分布规律,所以对双层植被水流应当进行分层研究。

图3 不同工况实验实测流速分布Fig.3 Experimental measurement of velocity distribution with different scenarios
相应Reynolds 应力数据如图4所示,从图4中可以看出,双层植被水流Reynolds 应力的分布呈现的规律性不多,不同测线之间,同一条测线不同水深之间的Reynolds 应力最多甚至相差两个数量级。但仍然可以发现,Reynolds 应力的取值在下层植被顶端出现了突变,即Reynolds 应力的分布在下层植被的顶层是不连续的。
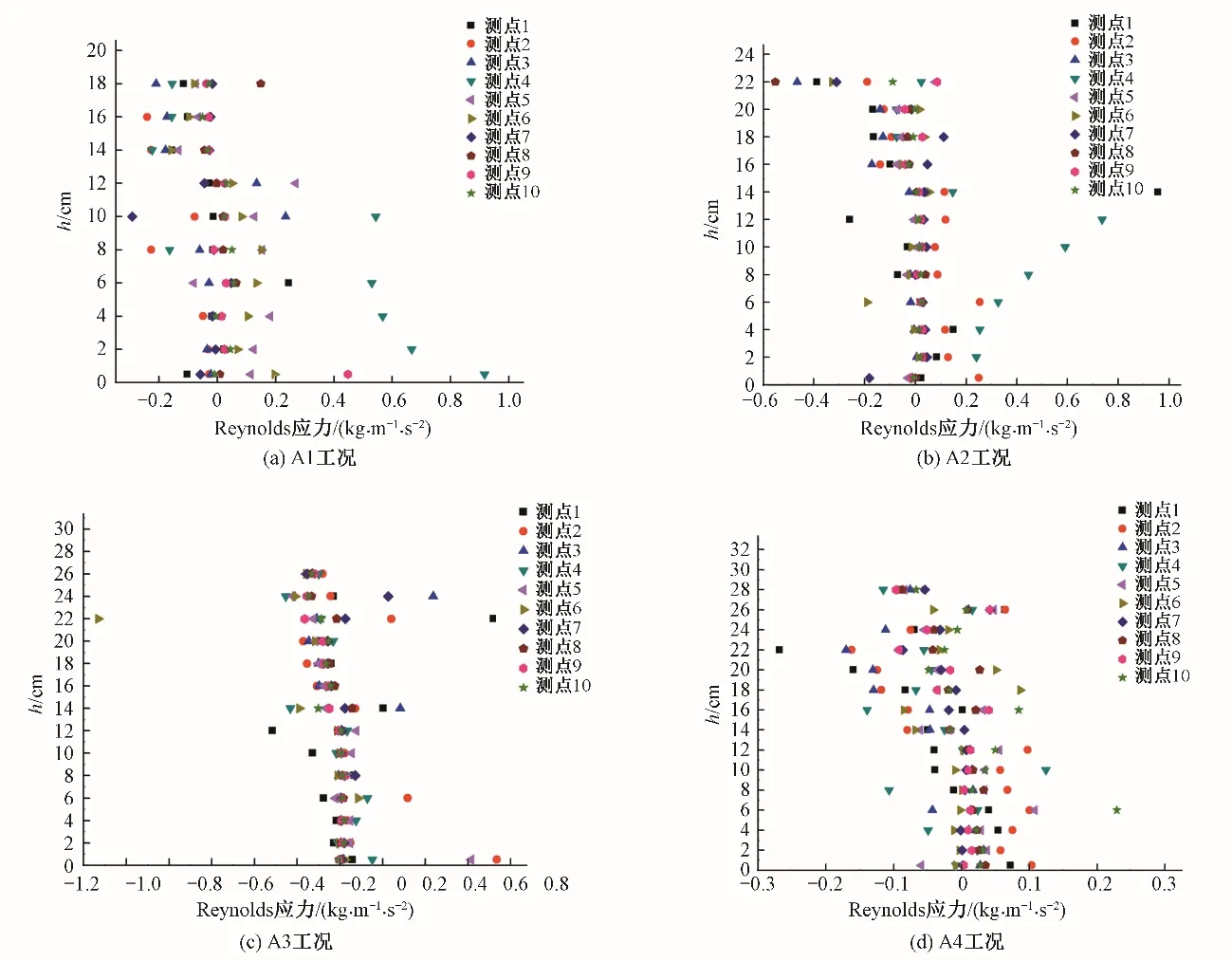
图4 不同工况实验实测Reynolds应力分布Fig.4 Experimental measurement of Reynolds stress distribution with different scenarios
2 研究结果
2.1 双层水流解析解数学模型建立
考虑双层非淹没水流(即高层植被没有被水流淹没),综合考虑黏性切应力,Reynolds应力及植被阻力的影响,双层非淹没水流共可分为4层,如图5所示。
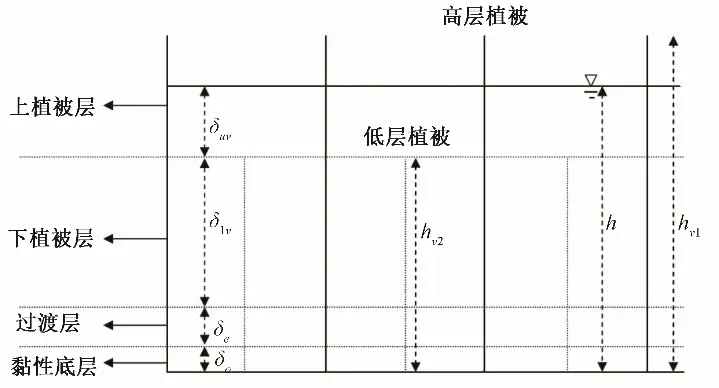
图5 双层植被水流分层示意图Fig.5 Stratified schematic diagram of water flow in double layer vegetation
在黏性底层中,黏性切应力起主导作用,Reynolds应力可忽略;在过渡层中,黏性作用已经大大减小,而由于植被的阻碍,水流的紊动性没有得到充分的发展,因而Reynolds 应力和黏性切应力均可以忽略;在下植被层及上植被层中,Reynolds应力起主导作用,黏性切应力可忽略不计,因此各层的动量方程分别为:
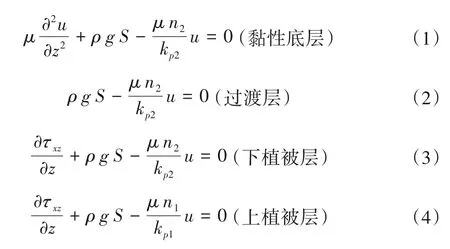
式中:μ为水的黏性性系数;u为主流方向的时均流速;x,z分别为主流方向及垂向坐标;ρ为水的密度;g为重力加速度;S为渠道的坡度;τxz为主流方向Reynolds 应力;n1,n2分别为上植被层及下植被层的孔隙率,计算公式分别为n1=1-Nv1Av1,n2=1-Nv2Av2-Nv1Av1,其中Nv1,Nv2为单位面积渠道内上植被层及下植被层的植被数,单位植株所占的断面面积Av1=πD12/4,Av2=πD22/4;kp1,kp2分别为上层植被及下层植被的多孔介质特定渗透率,其计算公式分别为:
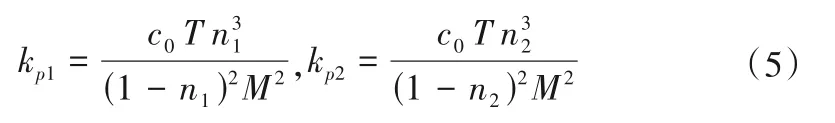
其中c0是Kozeny 常数,该常数在圆形断面中为0.5 在长直断面河道内为0.667,本文取c0=0.667;T是多孔介质的迂曲度,Carman[42]建议T取0.5;M是特征表面积,定义为表面面积与固体体积的比。植被越强壮,植被密度越小,M的取值就越大。对于水草类植物,M取103,对于植物的根系,M取104。双层植被研究中的M取值为从过渡层流速反推求得。在实验A1 中,下植被层取M=2 × 104,过渡层及上植被层取M=3.8 × 104;在实验A2 中,下植被层取M=2.2 × 104,过渡层及上植被层取M=4.0 × 104。
据Huai等[43],过渡层的厚度δe由经验公式:

决定,其中CD为植被拖曳力系数,其取值为:
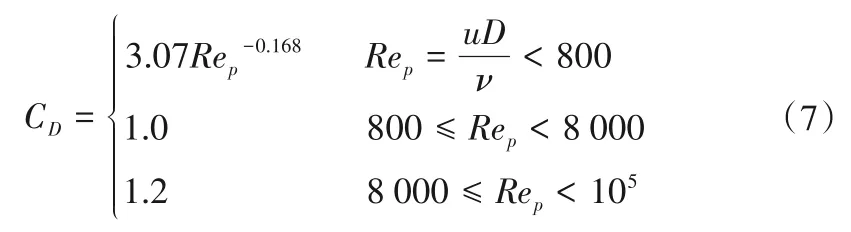
由方程(2),过渡层的动量方程的解析解为:

采纳Huai 等[43]的假定,将黏性底层的厚度δ0取为0.5 cm。由方程(1),黏性底层的动量方程解析解为:

其中系数C1和C2由边界条件确定,即黏性底层顶部u=,而渠道底部u=0。
下植被层的厚度δlv=hv2-δe-δ0,在下植被层,采用Ping和Yu[44]的假定,Reynolds 应力其中h为水深,β为紊动系数,其取值由试错法决定。因此,方程(3)可转化为:

设下植被层流速的解析解为级数形式,即:

将其带入方程(10)可解得各项系数间的关系式:

将方程(11)和方程(12)联立并代入边界条件,即已求得的过渡层与下植被层交界面处的u值,即可得到各项系数an的值。
在上植被层,由于植被密度的突然变化导致了水流紊动性的增强,而随着水深的增加,水流的紊动性又由于植被的作用而降低,所以将Ping-Cheng Hsieh 和Yu-Sheng Shiu 假定进行转化,在上植被层中取将上述τxz的表达式代入公式(4)可得:
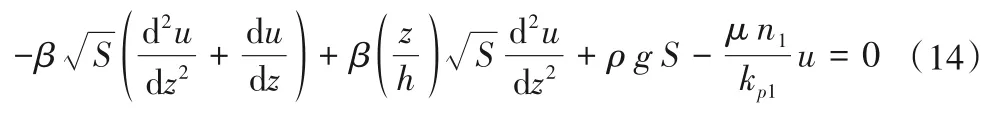
方程(14)的解析解为:

其中:
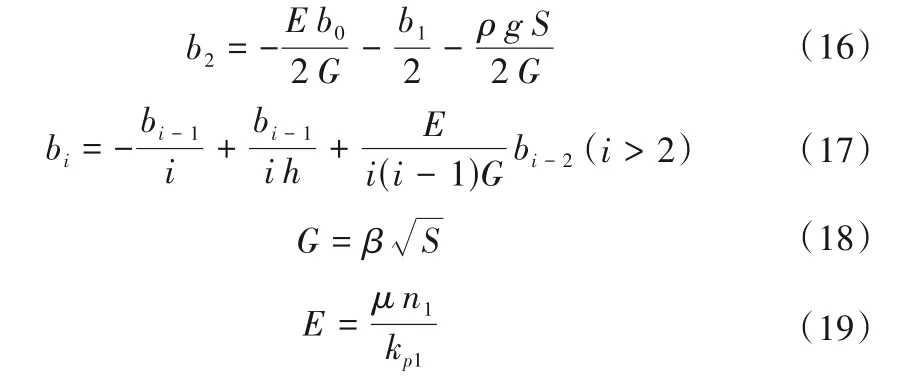
将方程(14)和方程(15)联立并代入边界条件,即已求得的上植被层与下植被层交界面处的u值,即可得到各项系数bi的值。上植被层的厚度δuv=h-hv2。
2.2 实验数据和模型计算结果对比
将试验数据进行平均,求出主流向的时均流速,并将A1、A2 两组实验的工况条件带入第3 章所求出的解析解,实验结果与解析解的对比情况如图6所示。
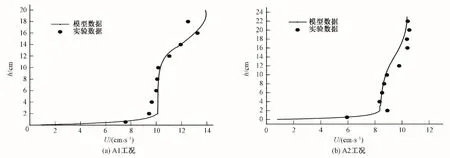
图6 两种工况实验数据平均值与计算结果对比Fig.6 The average value of the experimental data is compared with the calculated results with two scenarios
如图6所示,实验结果与解析解的结果吻合良好,说明非淹没植被水流的分层解析解可以很好的模拟双层植被水流的时均垂向流速分布。而与植被有一定距离,不受植被干扰的位置,流速与切应力分布与公式计算结果基本吻合;紧邻植被的位置,受植被影响较大,切应力及流速分布不规律,但可以明显得出切应力在柔性植被顶部不连续这一规律。在实验Run1中,下植被层β取值为60,上植被层β取值为10;在实验Run2中,下植被层β取值为70,上植被层β取值为12。
实验中的测线按照距离植被的远近,可分为两组,分组情况如表2所示。

表2 双层植被水流测线分组Tab.2 Flow measurement of double layer vegetation
图7为实验数据所测得的流速的平均值与计算结果的对比图,可以看出,计算结果可以反映远离植株的测线(B2)的垂向时均流速分布的趋势,而组紧贴植被的测线(B1)由于距离植株过近,受单株植被的影响太大,解析解并不能反映这些测线的垂向时均流速分布的趋势。
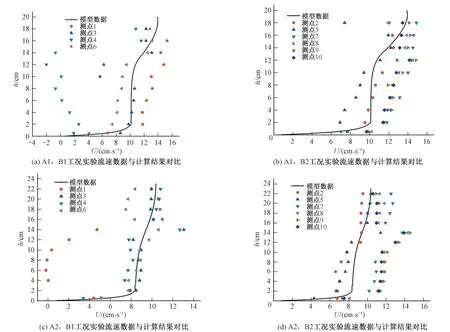
图7 不同工况实验流速数据与计算结果对比Fig.7 Comparison of experimental velocity data and calculation results of different scenarios
Reynolds 应力的实测结果如图8所示,无论测线是否邻近植株,Reynolds 应力的分布在不同的测线均有较大的差异。但可以看出,在低层植被的顶层,每条测线上的Reynolds 应力都发生了较大变化,即在低层植被顶层,Reynolds应力的取值是不连续的。这与模型中所假定的下植被层Reynolds 应力模型为上植被层Reynolds 应力模型为τxz=二者在低层植被的顶层取值并不连续相符合。
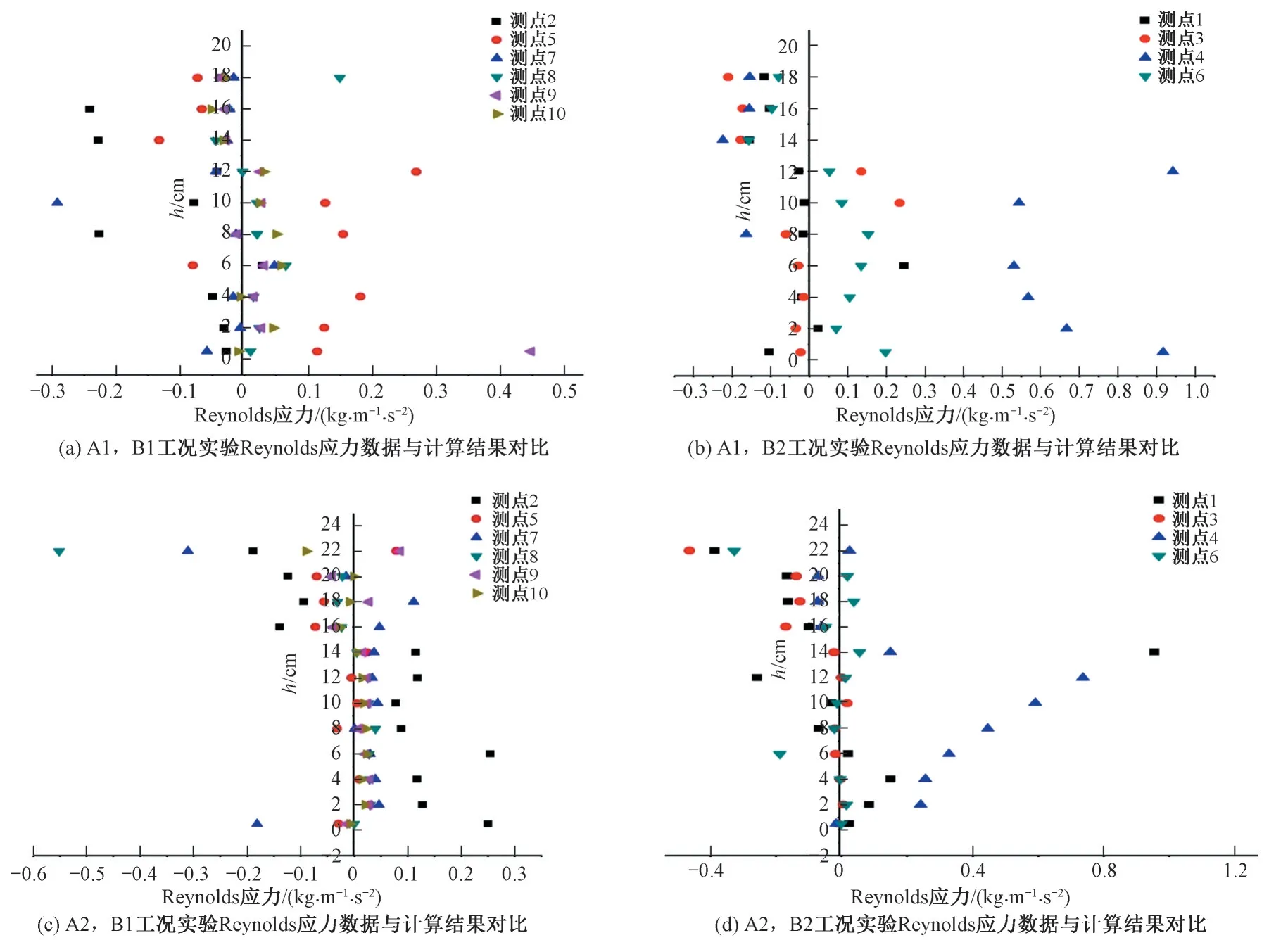
图8 不同工况实验Reynolds应力数据与计算结果对比Fig.8 Experimental Reynolds stress data and calculation results of different scenarios
3 结 论
(1)对淹没及非淹没双层植被水流进行了实验研究,通过分析实验数据,发现淹没与非淹没植被水流的流速分布在不同的水深区间具有不同的特性这一特点,进而指出应对非淹没双层植被水流进行分层研究。
(2)依据双层植被水流不同水深之间不同的水流特性,对双层植被水流进行了分层,并给出了每层的控制方程并求出了各方程的解析解;分析了双层非淹没植被水流的Reynolds 应力分布情况。同时给出了基于Micro ADV 测量的双层植被矩形水槽的紊流时均流速垂向分布的相关实验资料。结果表明,解析解可以准确预测双层植被水流的时均流速垂向分布以及远离植株的测线流速分布趋势。
(3)多层植被水流的各层之间,切应力由植被阻力,Reyn‐olds应力及黏性应力三部分组成,各层之间,这三种切应力的大小与在总切应力中所占的比例不同,因而在多层植被水流的研究中,应当对每层进行切应力分析,得出各层的主要切应力组成部分,从而舍弃微小量,对动量方程进行简化,进而求出垂向流速分布的解析解。
