心墙坡比突变对水力劈裂影响的离心模型试验研究

王艺洁，陶 虎，张少英，王军玺

（1.兰州交通大学土木工程学院，兰州 730070；2.西安理工大学土木建筑工程学院，西安 710000）

0 引 言

1976年，美国Teton 坝在蓄水初期失事，全程仅1.5 h，损失惨重，社会影响极大，经事故调查组勘查取证后，发现右岸齿槽内心墙土料出现拱效应，遂将其失事原因归结为水力劈裂引起裂隙发展，局部渗漏引起流土和管涌现象，最终引发溃坝。类似工程事故［1］还有挪威的Viddalsuatu 坝和Hyttejuvet坝、英国的Balderhead 坝、美国的Wister 坝 和Yard，s Greek 坝、加拿大的Manicouagan 坝和印度尼西亚的Djatiluhur 坝，以及中国的西斋堂坝，土质心墙坝的水力劈裂问题日益受到学者们的重视。

Seed［2］、黄文熙［3］均指出水力劈裂现象是指土体或岩体的裂缝在高压作用下产生并扩展的现象。因此在水力劈裂问题中，初始裂缝的形成是重要的物质条件之一［4，5］。在影响心墙出现裂缝的众多因素中，方达欧［6］认为土石坝心墙的几何形状是其中一个重要影响因素。比如挪威Hyttejuvet 坝在施工过程中监测到较高的孔隙水压力，为加快心墙孔隙水压力消散，在施工中途减小了心墙宽度，致使心墙结构异变，最终在初次蓄水期发生水力劈裂现象。研究表明心墙结构形态是影响水力劈裂发生的重要因素［7］，当心墙上游面形态呈现较大突变和转折时，会在心墙和坝壳料之间加剧拱效应现象，较易出现裂缝。因此，分析心墙坡比突变对坝体发生水力劈裂的影响便显得尤为重要。

土工离心模型试验可进一步贴合心墙的边界条件、应力路径和应力状态，近些年使用该项技术研究土体裂缝、沉降及水力劈裂的有效性已得到证实［8-10］。本文正是在此背景下提出，依托西南交通大学TLJ-2 型土工离心机，采用土石坝模型离心试验模拟坝体施工期及初次蓄水的工作状态，重点研究了心墙上游面突变段的应力分布情况，监测心墙上下游水压力及蓄水过程中心墙应力的变化过程，揭示初次蓄水时心墙发生水力劈裂的应力特征，通过有限元软件建立数值模型，运用总应力分析法分析竣工期和蓄水期心墙形态和上游面坡比不同对坝体拱效应的影响。

1 离心模型试验

1.1 试验模型箱

试验模型箱采用自制模型箱，尺寸为800 mm（长）×600 mm（宽）×600 mm（高）。模型箱底面及其他3 个侧面由钢板组成，另一侧面为便于观测试验模型运转情况采用有机玻璃，自制模型箱参数如表1所示。钢板外围采用肋条焊接以加固模型箱。试验模型处于水下环境，因此模型箱各接缝处的密封性十分重要，须涂抹密封材料。此次试验最大离心加速度为200g条件下，模型箱未出现肉眼可见的挠曲变形，也未观测到漏水现象，证明模型箱可用于此次水力劈裂试验。

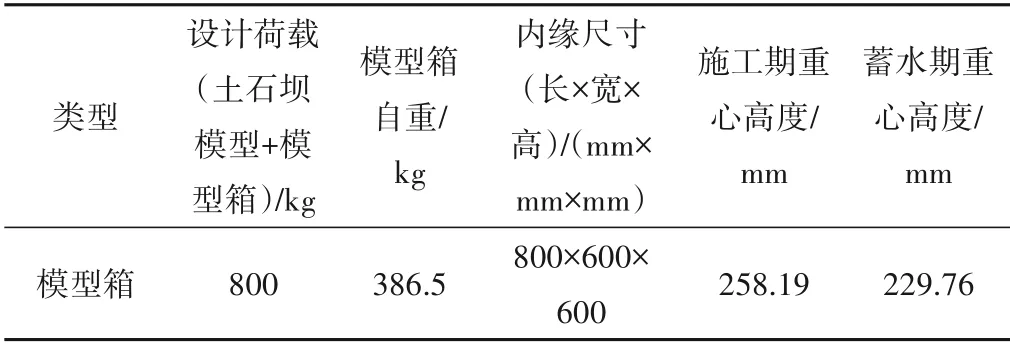
表1 模型箱主要参数Tab.1 Main parameters of the model box

装上土石坝模型后的模型箱正视图见图1，俯视图见图2所示。为防止箱体加载过程中出现模型侧壁与箱体接触面渗漏的问题，采用密封材料封堵密实，使用效果良好，试验过程中未出现侧壁渗漏。

图1 模型箱实拍正视图Fig.1 Sectional view of centrifugal model box

图2 模型箱实拍俯视图Fig.2 Top view of sensor layout

1.2 试验用土

现场实测资料分析表明，心墙坝工程的水力劈裂破坏均发生在初次蓄水期［11］，此时心墙尚未形成稳定的浸润线，为非饱和状态。只有在工程初期心墙土体处于非饱和状态才存在尚未消散的高孔隙水压力，使得土体竖向有效应力减小，水体进入裂缝后水压楔劈效应才易形成，最终产生扩展和贯通。为真实模拟施工期和初次蓄水初期土质心墙的非饱和状态，水力劈裂试验采用非饱和心墙土样，心墙防渗土料干密度为1.69 g/cm3，含水率18.25%，测定液限为39.5%，塑限为20.5%。考虑到要尽量减小模型试验中粒径效应和边界效应的影响，坝壳料试验干密度为1.89 g/cm3，孔隙率为22%，颗粒级配曲线图如图3所示。

图3 坝壳料级配曲线Fig.3 Grading curves of shell materials

模型填筑与原型建坝过程基本相似，采用分层填筑的方法，逐层夯实到设计干密度。对土层间接触面进行刨毛处理，确保相邻土层间接触良好。心墙土体两侧及底部与模型箱的接触面须在填筑土料前涂刷一层止水油脂，防止试验过程漏水。模型箱制好以后，吊入离心模型机中，检查采集系统是否正常，调整土压力和位移传感器，检查各通道、安全防护系统及加水系统。

1.3 试验步骤

模型坝的正视图如图4所示。模型坝高510 mm，其中防渗心墙上部宽50 mm，下部宽140 mm，坝顶宽76 mm。模型比尺取为1∶200，设计离心加速度为200g，等效坝高为102 m。为探究心墙变坡对水力劈裂的影响，在模型心墙上游面245 mm 处设置变坡，245 mm 以下坡比为1∶0.44，245 mm 以上突变为竖直心墙。

图4 土石坝模型正视图（单位：mm）Fig.4 Sectional view of centrifugal model box

模型箱中埋设5 支水压力传感器，上游左、右底面各一只（标号KY-2，KY-1），下游左、右底面各一只（标号KY-4，KY-3），245 mm 变坡处设一只（标号KY-5），设置3 支土压力传感器，分别位于上游坝壳处、心墙245 mm 变截面处水平和竖向各一只（TY-6、TY-7、TY-8），1 支位移传感器位于心墙顶端监测心墙沉降量（标号YWC-1），模型箱内传感器布置俯视图如图5所示。

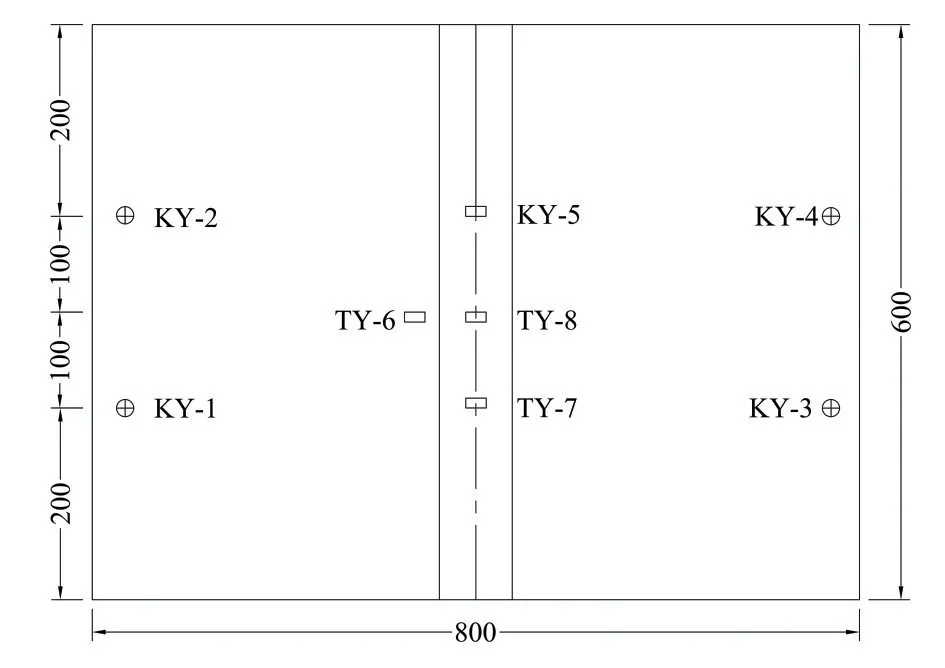
图5 传感器布置俯视图（单位：mm）Fig.5 Top view of sensor layout

模型运行分两个工况，即施工期和蓄水初期。运行前须确保试验设备安装正常，离心机开机后逐级加载升到200g，然后在200g下稳定转动，待变形趋于稳定后，打开加水阀门在模型上游注入掺入蓝色墨汁的水。试验结束后，能判定水力劈裂发生的现象如下：①土石坝模型下游出现蓝色水迹；②试验后拆模，查看心墙内部是否出现残留的蓝色痕迹，即水力劈裂形成的裂缝；③土石坝模型在未停机之前，上游安装的孔隙水压力传感器量测到水压突降，同时下游孔隙水压力传感器量测到水压突升。

试验后，第一组（模型A1）试验模型并未出现水力劈裂现象，分析是因为施工期运转时间太短，心墙土体沉降量太小，拱效应作用不明显。根据第一次出现的问题及不足，重新制模做了第二组（模型A2）离心模型试验，延长离心机运转时间以累积坝体不均匀沉降，最终出现水力劈裂现象，以下为两组试验结果的对比说明。

1.4 施工期模型分析

施工期，模型采用逐级从0g加载至16g、32g、64g、128g和200g的方式，模拟大坝逐级施工过程。模型A1 每级运转6 min，加到200g时再运转6 min，使得坝体固结。模型A2延长运转时长，每级运转12 min，加载至200g再运转12 min。两组模型上游坝壳、心墙处的土压力传感器TY-6、TY-8监测到这一过程的土压力随时间变化的曲线如图6所示。土压力均随模型加速度呈阶梯式变化，且同一高程处土压力传感器TY-6、TY-8监测到心墙土压力略高于坝壳土压力，为蓄水期心墙与坝壳不均匀沉降后产生拱效应提供力学条件。

图6 施工期竖向土压力-时间变化图Fig.6 Vertical soil stress vs.Time during construction

这一时期土料接近饱和，不断增加的自重荷载（上覆土压力）促使大坝土体内形成高孔隙水压力，并不断向低孔隙水压力区消散。当其消散速度小于增长速度，会造成孔隙水压力积攒，形成高孔隙水压力。进一步考虑到现代土石坝填筑速度快，心墙土渗透系数呈非线性特性，渗透系数较低的心墙土在固结及自重荷载作用下，其最终的渗透性往往低于原有工程设计值，使得孔隙水压力的消散变得更为缓慢和困难。这种高孔隙水压力的存在会大大降低心墙的有效应力。因此在施工期，土体不均匀固结和高孔隙水压力的存在都为水力劈裂的形成提供了物质基础。

1.5 初次蓄水期分析

1.5.1 模型水力劈裂现象

模型A1 在开机运转10 min 后打开电磁阀加水，每级加载时间6 min，同步逐级加载至200g后整体蓄水完成，运转30 min后停机。如图7（a）所示，模型A1 下游孔隙水压力并未突升，开挖后也未发现水力劈裂痕迹，而后总结经验调整模型加载时间。模型A2 分5 级加载，每级加载15 min，至200g后打开电磁阀向上游加水至预定蓄水位485 mm。运转至6 562 s 时，模型A2 出现下游孔隙水压力骤升，如图7（b）所示，即视为发生水力劈裂。模型A2 停机开挖后，心墙245 mm 水平面出现显著蓝色劈裂痕迹，见图8所示，即心墙变坡处出现显著的水力劈裂现象。开挖始末，如图9所示：心墙245 mm 处两端坝壳料均有蓝色示踪剂集中带，坝坡处距端部300 mm 处呈流塑状态，心墙左端边坡处水平向夹蓝色细沙，上、下游内伸0.5 cm 处整体呈流塑状态，最终导致渗透破坏。

图7 蓄水期水压力-时间变化图Fig.7 Water pressure vs.Time during storage period

图8 水力劈裂痕迹Fig.8 Hydraulic fracturing marks

图9 模型A2开挖实拍图Fig.9 Actual excavation image of Model A2

1.5.2 心墙变坡处水力劈裂机理初步分析

模型A2 试验过程中心墙顶端最大沉降量为919 μm，如图10所示。蓄水期土压力的增长曲线与施工期相比，如图11中土压力-时间变化与图6（b）所示明显不同，且蓄水期出现心墙变坡处水平土压力大于竖直土压力的情况。数据表明：在蓄水期5 010 s 时，上游坝壳土压力处于正常水平，相同高度处的心墙竖向应力值却徘徊在0.21～0.23 MPa之间，远小于该处施工期竖向土应力监测数值0.83 MPa，甚至小于同一高程处的心墙水平向土压力。证明该坝体模型出现较明显的拱效应及心墙应力各向异性。

图10 模型A2心墙沉降位移-时间关系图Fig.10 Model A2 displacement-time relation diagram of core wall settlement

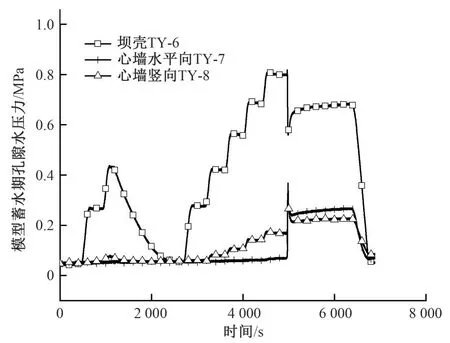
图11 模型A2蓄水期土压力-时间关系图Fig.11 Vertical soil stress vs.time of Model A2 during storage period

施工期时，一般认为心墙的大主应力与小主应力分别为竖直方向和水平方向，填筑时在大主应力方向施加上覆土压力。心墙两侧边缘部分土体受坝壳约束，应力矢量会发生轻微偏转［12］。蓄水期后水荷载作用于低渗透性的心墙上，该加载方式有异于自重加载，水荷载直接在心墙小主应力面施加，故对心墙小主应力的大小及分布影响比较大。竣工期时，心墙和坝壳料区的接触面附近拱效应又较为明显，尤其在心墙变坡处接触面剪应力变化较大，导致局部出现大主应力水平，小主应力竖直的情况。即经过初次蓄水后，心墙内部会出现应力重分布。

因此，分析施工期与蓄水期的孔隙水压力和土压力变化特征，认为水力劈裂首先是在竣工期因心墙土料与坝壳料物性指标差别较大造成不均匀沉降而形成显著拱效应，然后在初次蓄水时库水压力作用下，导致心墙上游表面裂缝的产生、扩展，最终形成贯穿的过程。

初期劈裂阶段，表现为心墙中的裂隙或缺陷成为渗透的优势通道，首先水体沿着渗透系数较大的坝壳料（无黏性土料）至黏土心墙前沿处。若黏性土中存在裂隙或缺陷，随着上游水位的升高，水压力进一步增高，由于裂隙或缺陷处的孔隙率高、密实度低导致渗透性较强，而碾压密实的结构面则孔隙率低、渗透性小，进而在心墙内局部产生不同的入渗速率，孔隙水压力在软弱界面处出现增大的现象，为产生楔劈效应提供了力学条件。劈裂后期，水压力仍然存在或继续上升，裂缝会在水压力的作用下持续扩展，压力下水流带出细小颗粒，发生管涌现象，最终形成较大直径的孔洞。结合试验结果，从水力劈裂判别准则方面讨论，传统观点认为拉裂判别准则为有效小主应力数值大于抗拉强度数值，该准则对局部微小裂缝适用，却忽略了库水压力作为劈裂动力的存在，与库水压力最终导致的水力劈裂发展的核心概念不符。因此，认为当心墙产生严重拱效应，致使竖向土应力小于库水压力时便会发生水力劈裂。

2 水力劈裂数值模拟

模型A2 试验结果表明，在初次蓄水期发生水力劈裂现象，且劈裂处恰为心墙变坡245 mm 处，为进一步分析心墙上游面坡比突变对水力劈裂的影响，使用有限元软件Geostudio 的应力-渗流耦合模块建立数值模型，土料的应力应变关系使用线弹性模型。水力劈裂的计算方法有总应力法、有效应力法和综合法［13-15］，试验中蓄水速度较快，可认为水压力为是瞬时加载的［16］，因此采用总应力判别法是比较合理的。

心墙黏土竖向总应力相对于计算上覆土压力偏小则表示坝体产生拱效应，相差越大则表示拱效应程度越严重。模拟坝体竣工期和初次蓄水期的拱效应变化过程，对比蓄水完成后的坝体拱效应程度与竣工期拱效应变化程度，分析水力劈裂发生在蓄水初期的原因。将上游库水压力是否大于相应高程处的土体竖向压力作为发生水力劈裂的判别依据。

因此设置3 个算例，算例1 坝型与离心模型试验中坝型一致，心墙上游面设置突变段；算例2 与算例3 仅改变心墙上游面坡比，分别为1∶0.20 和1∶0.25，并去除突变段，其他材料参数算例1 一致，用以对比说明心墙坡比变化后坝体应力状态及心墙位移的变化规律，材料参数如表2［17，18］所示，其中黏土心墙料和坝壳料物性指标与上文中试验模型一致。

表2 土石坝模型材料参数Tab.2 Material parameters of earth-rock dam model

提取以上3 组算例的上游面竖向应力，分析3 种坝型心墙上游面竖向应力与上覆土压力及静水压力的关系，并计算其相应的拱效应系数β（竖向土压力与上覆土压力计算值的比值），如图12、13所示。

如图12所示，算例1 竖向应力在高程48～58 m 之间出现竖向应力小于静水压力的情况，此处位于心墙坡比突变附近。而去除心墙突变段的两组算例则不同，竖向应力小于静水压力出现在73～98 m高程处，说明心墙为无突变形态的情况下，发生水力劈裂最危险的区域在心墙中上段，而有坡比突变的心墙形态，发生水力劈裂最危险的区域出现在坡比突变处。

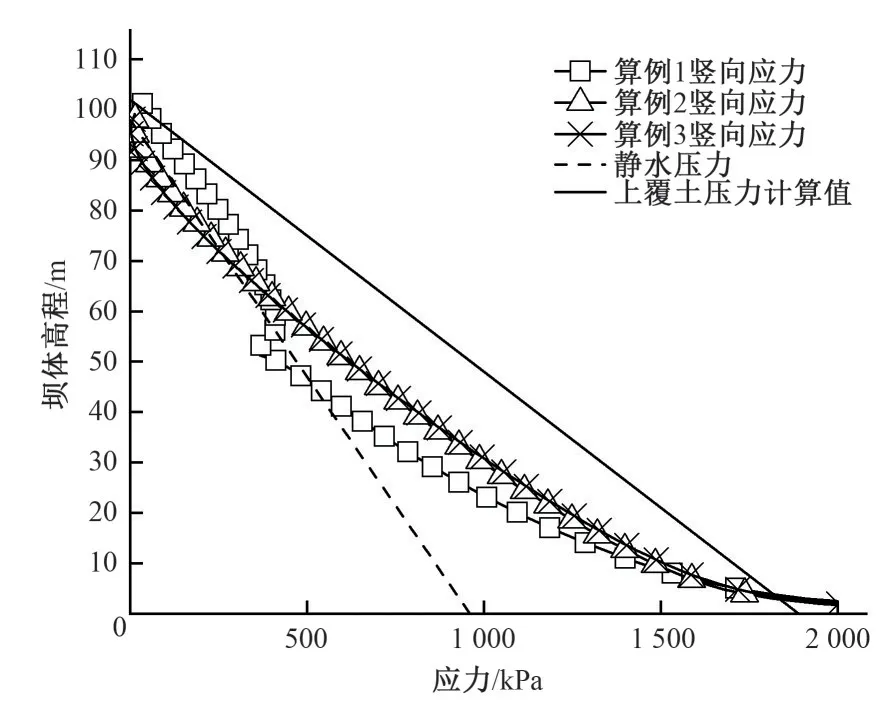
图12 心墙上游面竖向应力与静水压力关系图Fig.12 Relationship between vertical stress and hydrostatic pressure on the core wall

如图13所示，对比以上3 个算例心墙上游面的拱效应系数。有坡比突变突变的算例1心墙拱效应系数在突变高程52 m处骤降至0.43，竖向应力减小为357 kPa，说明此类心墙拱效应较为显著的位置在坡比突变处。在心墙上游面无突变的情况下，对比算例2 和算例3 的拱效应系数，同一高程处坡比越大拱效应系数越小，即坡比1∶0.25 的心墙上部拱效应比坡比1∶0.2的心墙要严重。说明无突变心墙拱效应较为显著的位置在心墙上部，这与Teton坝的水力劈裂位置相符。

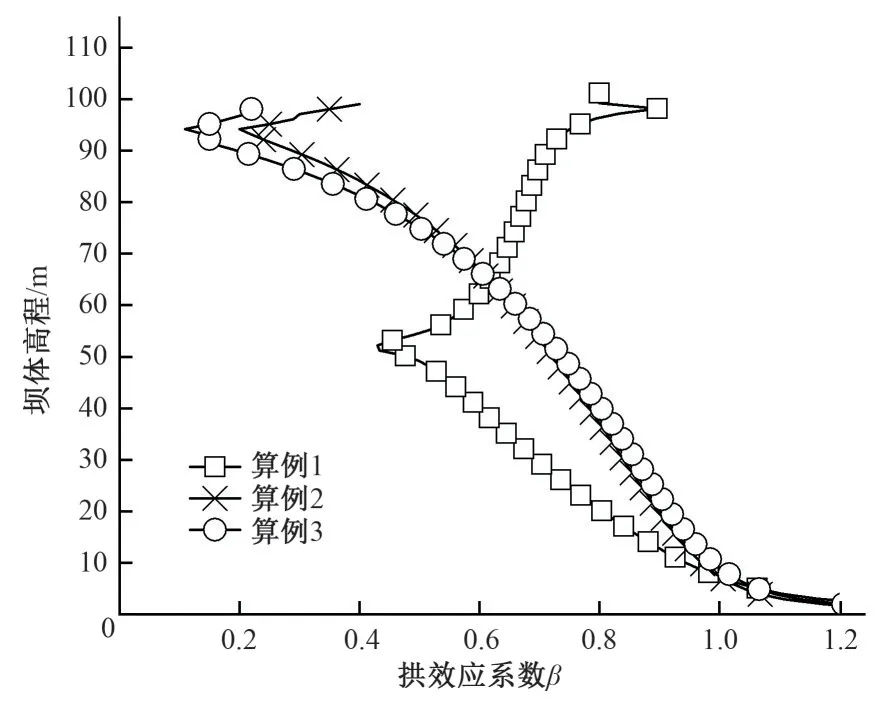
图13 心墙上游面拱效应系数对比图Fig.13 Comparison diagram of arching effect coefficient of upstream surface of core wall

3 结 论

结合室内离心机模型试验和Geostudio渗流-应力耦合模块分析了具有心墙坡比突变的土石坝水力劈裂形成机理，得出以下结论：

（1）离心机试验中，模拟了土石坝心墙坡比突变处在施工期与初次蓄水期的应力状态，成功再现心墙坡比突变处水力劈裂现象，心墙与坝壳土料力学性质的差异性为蓄水期坝体产生拱效应提供物质条件；

（2）离心机试验过程中，在心墙坡比突变处监测到的初次蓄水期应力特征值与施工期截然不同，离心机试验后期，突变段因不均匀沉降及结构异变，形成扰动应力场，应力发生偏转，出现竖直方向应力小于水平应力的情况。证明在水力劈裂发生过程中，劈裂部位存在较明显的拱效应及心墙应力各向异性；

（3）对比施工期与蓄水期的心墙应力特征，表明蓄水后出现心墙应力重分布，根本原因在于施加侧向水压力与不均匀沉降；

（4）建立土石坝渗流-应力耦合模型，调整心墙形态及坡比，结果表明：心墙形态变化比心墙上游面坡比变化对拱效应的影响更显著。上游面无突变心墙拱效应最严重的位置在85m高程以上，有突变的心墙拱效应最严重的位置则在突变处。因此在坝型设计中应尽量避免心墙上游面出现坡比突变的情况，提高心墙坡比也有利于增强土石坝的抗水力劈裂能力。