饱和铁氧体界面附近的原子Casimir-Polder扭矩效应
2022-07-27胡悦曾然徐思远陈伟强李浩珍杨淑娜李齐良羊亚平
胡悦,曾然,徐思远,陈伟强,李浩珍,,杨淑娜,李齐良,羊亚平
(1 杭州电子科技大学 通信工程学院,杭州 310018)
(2 同济大学物理科学与工程学院 先进微结构材料教育部重点实验室,上海 200092)
0 引言
微观粒子的van der Waals–Casimir 和Casimir-Polder 效应一直是近年来深入研究的课题。电磁场的零点能量子涨落会导致van der Waals 力[1],1948年CASIMIR H 在理论上指出,边界表面的变化导致电磁场零点能的扰动,宏观上可以观察到作用在物体上的力[2]。对于各向异性媒质,Casimir 力可能随媒质之间的相对方向而变化,这种变化导致了相对旋转,称为Casimir 扭矩[3-5]。目前关于Casimir 效应的研究已经涉及到多种各向异性材料,例如双折射材料[6-7]、特异材料[8-10]和各向异性拓扑绝缘体[11]等,测量转矩的实验装置[12-15]也被提出。CASIMIR H 和POLDER D 还给出了原子和理想导体板之间的力,在宏观板边界的存在下,处于基态或激发态的原子会受到Casimir-Polder 力的影响;而在各向异性媒质边界和原子之间,同样会产生Casimir-Polder 旋转扭矩。这类量子真空诱导扭矩是量子光学领域的重要研究课题之一,在物理化学、原子光学和腔量子电动力学等众多领域中都具有重要影响,并且在纳米技术中的许多潜在应用里同样发挥作用,例如构造原子力显微镜或反射原子光学元件[16-17]。
饱和铁氧体是近年来不断发展的一种具有铁磁性的非金属复合氧化物材料,其电阻率和介电性能等方面要优于常规金属磁性材料,铁氧体被广泛应用于卫星通信设备、精密仪器、控制技术等通信电子领域[18]以及光子晶体[19]等光学材料中。铁氧体在较高的频率范围内具有较大的磁导率,因此铁氧体在高频弱电领域也具有广泛的用途。另一方面,微波吸波材料作为一种新型材料在节能减排,人工智能和军工技术等方向发挥着重要的作用,而铁氧体材料既具备磁吸收能力又具备电吸收能力,并且其在吸波层厚度和频带宽度等方面优于其他吸波材料,因此铁氧体吸波材料也是现阶段的热门研究材料[20-21]。由于铁氧体的独特电磁特性,其附近原子的Casimir 效应和Casimir-Polder 效应与其他材料环境相比必然有较大不同,目前对于饱和铁氧体附近产生的Casimir 排斥效应和平衡回复效应[22]以及多层铁氧体结构系统的Casimir 扭矩[23]已进行了研究分析。由于铁氧体具有外场受控特性,进而可以通过外磁场来控制原子的Casimir-Polder 扭矩,本文将对二能级原子与饱和铁氧体材料板之间的Casimir-Polder 扭矩进行计算和讨论,给出原子位置、跃迁频率、铁氧体所处外场强度对扭矩的影响,并计算分析在一定微扰下旋转扭矩的平衡稳定性。
1 Casimir-Polder 扭矩理论计算
考虑一个二能级原子位于一块饱和铁氧体板附近的情况,如图1所示,原子位置为rA=(0,0,zA),z轴分量为zA(zA>0)。图中实线箭头为Casimir-Polder 扭矩方向,虚线箭头表示xoz平面上诱导旋转的方向。

图1 二能级原子和饱和铁氧体材料表面间Casimir-Polder 扭矩示意图Fig.1 Schematic diagram of Casimir-Polder torque between a two-level atom and saturated ferrite material surface
按照经典扭矩的定义,作用于某偶极子的光学扭矩来源于其偶极矩与所处电磁场量的矢积。其中,将偶极矩与电磁场推广到量子化的算子[24],即可以得到量子光学扭矩表达式为
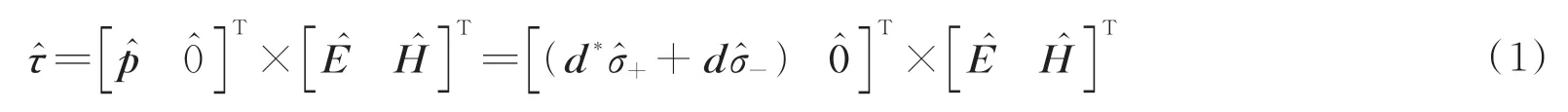
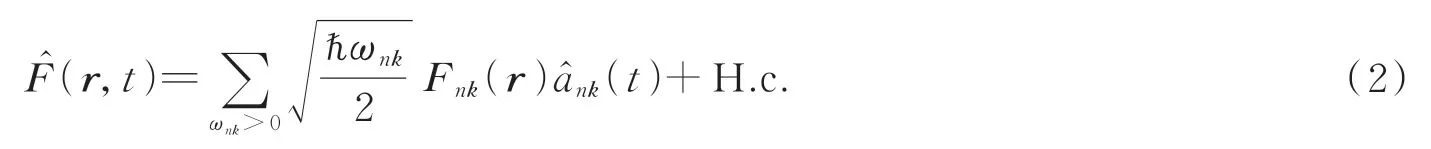
式中,Fnk为展开的场模,是湮灭算符,由海森堡运动方程给出,为系统哈密顿量。如果考虑到马尔科夫近似,可以表示为[25]
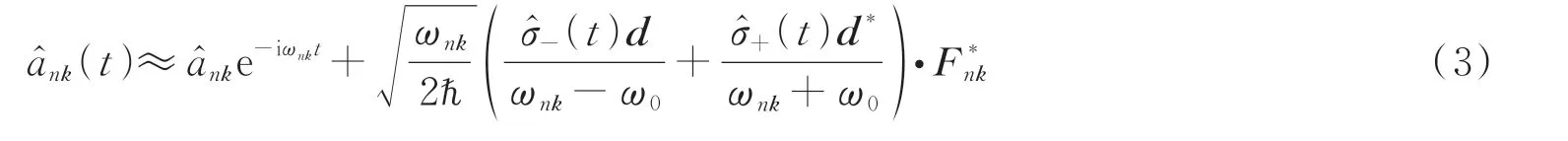

式中,和分别为量子光学扭矩的共振部分和非共振部分,即为Casimir-Polder 扭矩,对应系统初态处于原子基态,因为其包括真空涨落场全频段模式的贡献,可通过系统的格林函数张量[27]来描述二能级原子系统的Casimir-Polder 扭矩为
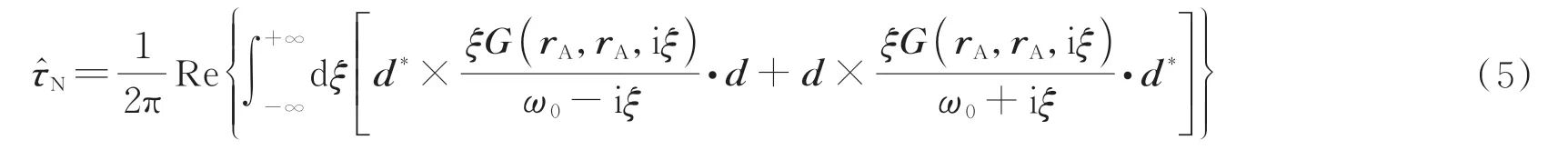
其中对此非共振部分的扭矩进行了虚频变换,ω→iξ。存在宏观饱和铁氧体界面边界的环境下格林张量G可表示为

式中,r为铁氧体反射系数,它是入射极化和反射极化的混合,下标s 和p 分别表示垂直极化和平行极化,z表示点源与界面的垂直距离,k‖表示波矢的平行分量,k⊥表示波矢的垂直分量。单位向量eσ+和eσ′-分别表示入射波极化和反射波极化,与坐标系矢量的关系为
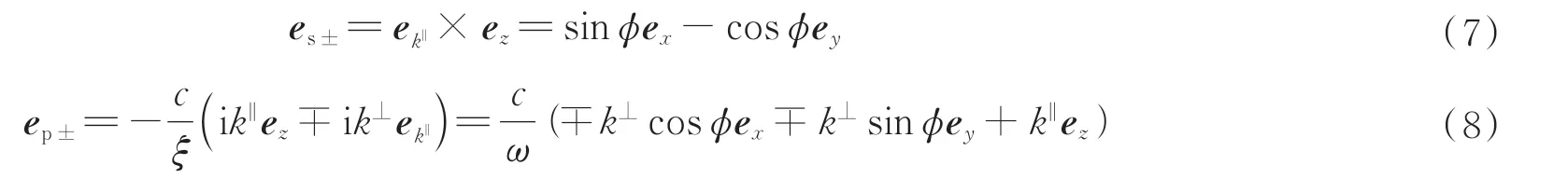
再将格林函数代入式(3),并选取典型的原子偶极矩计算二能级原子和饱和铁氧体板之间的Casimir-Polder 扭矩。
1)当选取原子偶极矩为

即圆极化偶极矩,极化面为xoy平面。经计算推导可得,各方向的扭矩为
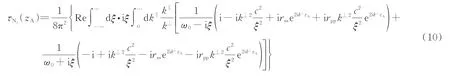
以及τNx=τNy=0。
2)当选取原子偶极矩为

即xoz平面内的圆极化偶极矩。该偶极矩下的各方向的扭矩为

以及τNx=τNz=0。
3)当选取yoz平面内圆极化偶极矩时

可类似地得到,y、z方向上扭矩为零,即τNy=τNz=0,而x方向上扭矩与式(10)中的τNy(zA)幅值相同但符号相反。另外,计算发现,当选取原子偶极矩为线极化时,Casimir-Polder 扭矩为零。
2 数值计算与分析
介质的电磁响应受介电常数ε和磁导率μ共同影响,当ε>μ时,介质表现出强电特性,当ε<μ时,介质表现出强磁特性。铁氧体是具有强磁特性的各向异性介质材料,即在铁氧体周围各个方向上施加不同强度的磁场时,铁氧体的磁导率会随着外加磁场的强度和方向而改变。当铁氧体材料磁饱和时,可通过式(14)来调节铁氧体的磁导率:

式中,ωex=γHex,其中Hex为外加磁场的强度,γ为旋磁比,即自旋磁矩和自旋角动量的比值;参量ωm=4πMS,其中MS为饱和磁化强度。通常情况下,典型铁氧体的介电常数的值在12~16 之间,而饱和磁化强度的值为135 G 到239 G 之间,旋磁比率的取值为1.8×107s-1G-1。本文涉及的频率将均以铁氧体的特征频率ωm为参考单位,而所涉及到的长度距离则以其相应波长为参考单位
首先考察不同的原子跃迁频率下,原子位置对二能级原子和铁氧体之间Casimir-Polder 扭矩的影响,如图2。本文选取铁氧体的介电常数为12,并且取扭力的单位为τ0=1/(128π2λ2m)。取外场特征频率参数为ωex=5ωm,图2(a)、(b)四种不同颜色的线分别代表原子跃迁频率为0.5ωm,1.0ωm,2.0ωm,3.0ωm。图2(a)显示了二能级原子的偶极矩为d=(1 i 0)T时,原子和铁氧体之间的Casimir-Polder 扭矩随着原子位置的变化情况,此时原子和铁氧体之间只有z方向上的Casimir-Polder 扭矩,原子和材料板的距离较近时,扭矩幅值很大,随着距离的增加,扭矩逐渐减小至0,这是由于原子距离材料板越远,Casimir-Polder 作用势越小,因此旋转扭矩效应越弱,这也类似于其他Casimir 压力作用或Casimir-Polder 相互作用力的规律。图2(b)是二能级原子偶极矩为d=(1 0 i)T的情况,此时只存在y方向上的Casimir-Polder 扭矩,随着原子与材料板的间距逐渐增大,扭矩急剧变小直至为0。y轴上产生的扭矩方向为负,这和原子偶极矩的选取有关,同时,原子偶极矩的选取也会影响扭矩的幅值,偶极矩为d=(1 0 i)T的情况下扭矩的幅值相对来说更强一些。从这些变化曲线也可以看出在不同的原子频率下,扭矩的距离依赖性大致都是上述的递减趋势;而当频率越高,Casimir-Polder 扭矩越小。

图2 二能级原子和铁氧体之间Casimir-Polder 扭矩随原子距界面位置的变化曲线(插图:较短距下的曲线)Fig.2 The Casimir-Polder torque between two-level atom and ferrite plate versus atomic position(insets:the curves at shorter distances)
为验证图2中扭矩随频率影响变化的单调性,取固定的原子位置,考察频率连续变化下Casimir-Polder扭矩受到的影响,结果如图3所示,四条不同颜色曲线分别表示原子与材料板间距为0.2λm,0.3λm,0.5λm,1.0λm。图3(a)为原子偶极矩d=(1 i 0)T的情况,随着原子跃迁频率的增加,Casimir-Polder 扭矩单调递减至0,并且对于不同的原子位置,原子和材料板之间的间距越大,Casimir-Polder 扭矩越小。图3(b)选取原子偶极矩为d=(1 0 i)T,y轴上的Casimir-Polder 扭矩方向为负,而幅值同样随频率升高而衰减。也可以看到xoz平面内的偶极子扭矩的幅值相对来说更强一些。Casimir-Polder 扭矩随频率变化表现的单调递减行为,与原子与板距离的单调影响相似。

图3 二能级原子和铁氧体之间Casimir-Polder 扭矩随原子跃迁频率的变化曲线Fig.3 The Casimir-Polder torque between two-level atom and ferrite plate versus atomic transition frequency
饱和铁氧体作为一种强磁性介质,磁导率受外加磁场的影响,因此接下来考察不同的外磁场对二能级原子和铁氧体之间Casimir-Polder 扭矩的影响。当固定原子与材料板的间距为zA=0.5λm时,分别选取原子跃迁频率为ω0=0.5ωm,ω0=1.0ωm,ω0=5.0ωm,计算得到的二能级原子和铁氧体之间Casimir-Polder 扭矩随外场特征频率参数ωex的变化曲线如图4。一般来看,Casimir-Polder 扭矩是随铁氧体的外加磁场的增强而变大的,从图中也可以看出,随着外磁场增强,z轴正方向上的扭矩和y轴负方向上的扭矩幅值都在逐渐增加并趋于一个饱和值,并且y方向上的扭矩比z方向略大。另外比较每个图中的三条曲线可以看出,原子跃迁频率较小时,扭矩幅值的变化曲线相对来说较平缓,原子频率较大时,曲线会在某些特定位置呈现急剧变化。

图4 二能级原子和铁氧体之间Casimir-Polder 扭矩在不同原子频率下随ωex 的变化曲线Fig.4 The Casimir-Polder torque between the two-level atom and the ferrite as functions of ωex for different atomic transition frequencies
当固定频率为ω0=2.0ωm时,分别选取原子与材料板的间距为zA=0.1λm,zA=1.0λm,zA=5.0λm,计算得到二能级原子和铁氧体之间Casimir-Polder 扭矩随外磁场变化曲线如图5。同样随着外磁场频率的增加,Casimir-Polder 扭矩逐渐增加并趋于一个饱和值,并且很容易看出,原子距离铁氧体越近时,扭矩幅值会在某些参数范围出现急剧变化行为。
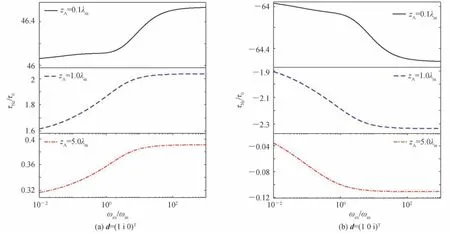
图5 二能级原子和铁氧体之间Casimir-Polder 扭矩在不同原子位置时随ωex 的变化曲线Fig.5 The Casimir-Polder torque between the two-level atom and the ferrite as functions of ωex for different atomic position
实际上,随着原子跃迁频率增大或原子越向材料板靠近,Casimir-Polder 扭矩随外磁场影响递增的单调性在逐渐发生变化,这种变化是一种偏离线性单调的趋势:在外磁场取某强度附近,或原子在某位置附近,扭矩会出现一种集中的急剧变化的倾向,其表明了非单调的拐点的倾向。但在图4和图5的结果曲线中,暂时还未出现非单调的变化性。若继续增大原子跃迁频率或减小原子与材料板的间距,就可以观察到单调性的改变,如图6。

图6 二能级原子与铁氧体间的相对Casimir-Polder 扭矩随ωex 的变化曲线Fig.6 The relative Casimir-Polder torque between the two-level atom and the ferrite as functions of ωex
图6对z方向和y方向的计算都采用了相对扭矩的幅值:即图中的曲线都显示非单调行为,在原子位置和原子跃迁频率都不同的情况下,随着外磁场的增大,Casimir-Polder 扭矩一般会先减弱再增强,呈现了一个随外磁场强度影响的“拐点”(而实际上某些曲线是存在两个拐点的,即还有一个从递增到递减的微弱变化)。也就是说,在外磁场强度取某值前后,扭矩增强或减弱的变化受磁场的影响是相反的。这表明:当用Casimir-Polder 扭矩效应来调控原本固有或已存在的某原子旋转态时,如果在如图曲线拐点的外磁场强度对应的扭矩恰好可以抵消原子固有旋转态的话,那么此时再调整外场强度,增大或减小该强度,都可以使原子向相同方向旋转。
以上考虑的二能级原子皆为理想的圆极化偶极子,若假设偶极子极化平面受到某种微扰,以xoy面的偶极子为例,使得偶极矩变为即极化平面从xoy面倾斜了一个微小偏转角度±Δ。通过计算发现,此时z方向上的扭矩大小并没有受到偏角扰动的影响,但z方向不再是唯一的扭矩方向,以x方向为例,将由于偏角扰动而产生如下非零扭矩
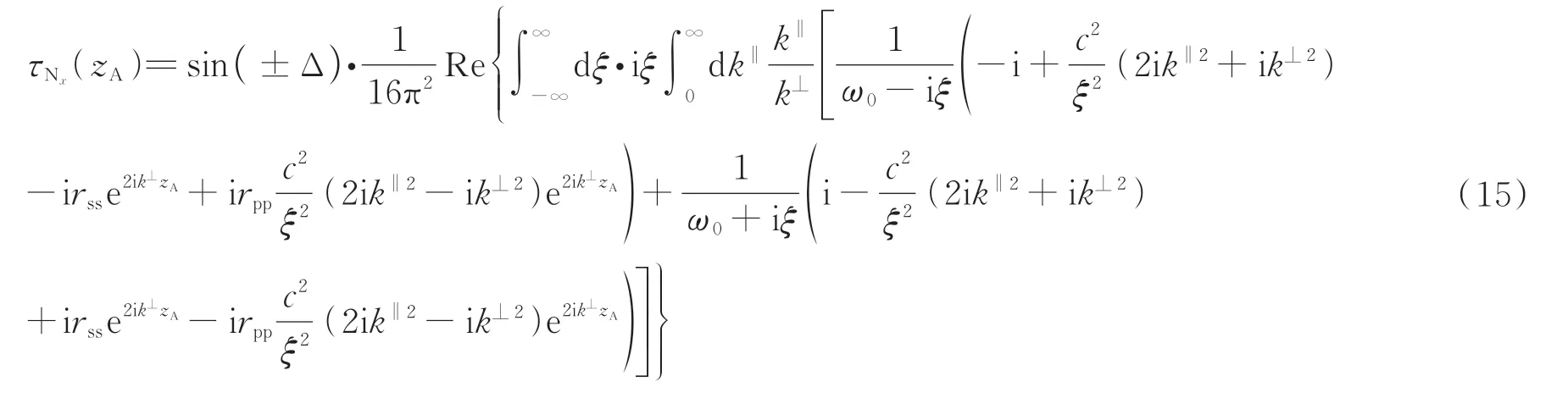
此时,固定原子与材料板的间距zA=1.0λm,外磁场ωex=5ωm,考虑原子跃迁频率对Casimir-Polder 扭矩x分量的影响,计算结果如图7。观察图中曲线可以发现,偶极矩主要在xoy平面,但沿着z轴有一个较小的分量,当偶极矩的z分量为sin( ±Δ)时,沿着x轴就会出现一个相应的负(正)扭矩,该扭矩将极化平面推回xoy平面,从而保持一种平衡状态——即尽管原子偶极矩极化平面受到微小角度扰动,使得Casimir-Polder 扭矩的方向偏离该平面,但是扭矩还是具有回归原旋转平面的趋势。
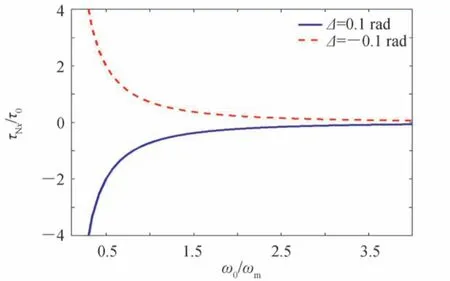
图7 圆极化偶极子极化平面受到微小角度±Δ 扰动下的Casimir-Polder 扭矩随原子频率变化曲线Fig.7 The Casimir-Polder torque versus atomic transition frequency under the perturbation of ±Δ on the circular polarization plane
3 结论
本文对二能级原子和饱和铁氧体材料板之间Casimir-Polder 扭矩进行了计算,通过旋转扭矩在量子化电磁场下的形式和格林张量求得Casimir-Polder 扭矩的具体表达式。研究了铁氧体材料板附近原子的扭矩在二能级原子的特征参数、所加外场以及偶极子所受微扰等因素影响下的行为。分析结果表明,Casimir-Polder 扭矩随原子位置和频率的变化分别都表现单调递减特性,而铁氧体所处环境的外磁场强度可以影响扭矩变化的单调性,扭矩随外磁场的变化曲线会呈现非单调的拐点。因此,当用这种扭矩效应来调控某原子固有旋转态时,如果在曲线拐点对应的扭矩恰好可以抵消固有旋转态,那么此时再调增或调减外场强度,都可以使原子向相同方向旋转。另外,一定的角度微扰下的圆极化偶极子,其扭矩具有回归原旋转平面趋势的平衡稳定性。Casimir-Polder 扭矩可在一些例如加速二能级系统的旋转态或将其冷却至量子基态等实际应用中发挥重要作用,而采用饱和铁氧体作为原子附近宏观边界的方案对原子的Casimir-Polder 扭矩提供了一种外场操控性。
