基于卷积神经网络的指纹条纹图相位提取方法

王海霞，单鲁斌，庞巧玲，张怡龙

（1 浙江工业大学 计算机科学与技术学院，杭州 310000）

（2 浙江工业大学 信息工程学院，杭州 310000）

0 引言

生物特征识别技术是利用人体固有的生理或行为特征来识别或者验证个人身份的技术。近几年生物特征识别技术［1］中指纹识别技术具有普遍性、可靠性、唯一性、永久性、可采集性、可行性等特点，是生物特征识别领域的研究热点。传统的接触式指纹采集多是通过按压或者滚动采集方式［2］，由于被采集者按压力大小的不可控和之前指纹采集所留下的残留物等问题，往往使得采集数据不理想。为了消除接触式采集而导致指纹失真问题，同时为了获取多维度指纹信息，近年来许多研究者试图应用非接触式采集方式获取三维指纹信息［3］。

目前常用的三维指纹采集技术有三种，即三维指纹重建［4］、结构光成像［5-6］和超声扫描［7］。在三种技术中，重建技术具有系统构成简单、成本低的优点。基于超声的三维指纹图像分辨率高，但特征提取与匹配识别难度大。相对而言，虽然结构光成像技术在收集三维数据时要求人的手指保持静止，但它具有精度高、成本适中的优点，因此广泛应用在三维指纹采集中。

在结构光成像技术中，条纹投影技术受到广泛欢迎和应用。条纹投影技术将余弦条纹通过数字投影仪投影至被测物，利用相机拍摄条纹因物体形貌产生的弯曲图像，解调该弯曲条纹得到相位，再将相位转化为目标三维信息。该技术核心算法是对采集得到的条纹图像进行相位提取。目前对条纹图像相位提取方法有傅里叶变换轮廓术［8-11］、相移法［12-15］和神经网络方法［16-26］等。傅里叶变换轮廓术由TAKEDA M 等［8］提出，常用在单幅条纹的相位计算中；FU Y 等［9］对传统的傅里叶变换进行改进，减少了三次频移，减少了计算时间，提高了滤波精度；PODDER P 等［10］对汉明窗、汉宁窗和布莱克曼窗的性能进行了比较，针对相位模糊问题进行改进；MA J 等［11］提出了根据相位分布连续性的相位确定规则，然后根据常规二维小波变换分析提出频率引导方案以获得正确的相位分布，但傅里叶变换轮廓术仍存在着对背景光和噪声敏感。相移算法是用于三个以上的条纹图案中并且需要知道每个条纹图像之间相移，从而可以准确的给出相位信息，对于静态三维测量具有较好的表现［12］。许多相移算法被提出和扩展，例如将格雷码和四步相移相结合实现相位计算［13］、基于导数算法的同步双波长三帧相移干涉相位提取方法［14］和结合超分辨条纹图像重建技术和五步相移算法获取相位信息［15］，在这些算法中，标准的N步相移算法因其在噪声抑制方面的优异性能而应用最广泛。为了获得较高的测量分辨率和精度，相移法通常是最佳的选择。

同时在近几年，随着计算设备和云资源上计算能力的不断提高，应用人工智能技术实现对数据智能处理是一个全新的解决方案。许多三维领域学者尝试将神经网络技术引入到三维测量中。神经网络主要分为两个阶段进行，第一个阶段是获取足够实验所需的数据，第二个阶段是搭建神经网络框架对实验数据进行训练，从而实现输入和输出的映射。在众多成功案例中，人工智能已在三维表面测量中得到证明，在相位展开［16-17］、高速轮廓测量［18］、镜头畸变校正［19］、单次轮廓测量［20-21］、ToF 三维成像［22］等领域表现都很出色。在相位解调方面，FENG S［23］等构建两个CNN 结构预测条纹相位图的正弦与余弦形式，然后通过反正切计算相位值。YIN W［24］等使用经过适当训练的深度神经网络，从单个条纹图像中预测相位信息，然后将其转换为三维形状。QIAN J［25］等将彩色条纹投影引入三维轮廓检测，将三种不同波长的条纹图像投影到检测目标表面，将采集到的图像分成三个通道，输入网络预测分子的相位反正切函数分母和绝对相位最终将误差降低到几十微米。HU W［26］通过U-Net 网络修改实现了从条纹图像到相位提取的过程。

本文针对条纹投影技术展开非接触式指纹三维测量研究，搭建了非接触式三维指纹采集系统，构建卷积神经网络对指纹相位图进行提取，并针对如今主流的相位提取神经网络中包裹相位2π 间断处误差剧增难优化问题展开研究，构建了新的包裹感知的损失函数对该区域进行约束，从而提高网络在2π 间断区域预测的准确性。

1 系统搭建与数据集建立

1.1 条纹投影三维指纹测量系统

三维指纹测量主要包含数据采集和数据训练两个部分，数据采集部分主要由DLP（Digital Light Processing）投影仪、相机和计算机组成。DLP 投影仪选用的是德州仪器开发的DLP LightCrafter 4500 投影模块，相机采用的是ASI183MM Pro 黑白相机，相机的镜头配备的是12～36 mm 变焦，型号为Computar M3Z1228C-MP。

本文搭建的三维指纹测量系统如图1所示。条纹投影技术获取随被测物体形貌变化的条纹图案，根据对应的相位信息计算点云深度信息。在实际进行三维指纹测量的过程中，对计算机生成的条纹图像在投影过程中存在Gamma 误差，本文采用Gamma 校正方法［27］进行消除；考虑到采集的指纹条纹图绝大部分为背景区域，为降低背景因素的干扰，本文对采集获取得到的指纹条纹图像进行感兴趣区域提取［28］，从而获取得到指纹有效区域。

图1 三维指纹采集平台Fig.1 3D fingerprint collection platform

1.2 数据集建立

神经网络算法需要大量的数据进行网络训练和测试。本文搭建的硬件采集系统采集手指条纹图像，并采用相移法获取相位作为真值。目前广泛使用的相移法有两步相移［29］、四步相移［30］等。相移的步数越多，相位提取的精度越高、抗噪声能力也越强，然而过多的步数会导致在一次图像采集中需要采集的图像大幅增加，采集时间变长，难以保证被测手指处于静止状态。因此，综合各方面因素，本文采用四歩相移算法计算相位值作为真值。

相机拍摄得到的条纹图像表示为

式中，A(x，y)表示背景光强，B(x，y)为待测物体表面的反射率，φ(x，y)表示条纹的相位值。四歩相移法拍摄四幅条纹图像，每幅图像相差π/2 相位差，因此可以联立式（2）四个相移条纹灰度图像公式获取得到真实的相位值。

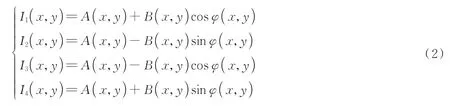
联立之后再通过反正切函数，计算得到相位值为

由于本文针对三维指纹进行研究，测量得到的条纹图像类型集中，因而全部采用真实测量得到的指纹条纹图进行训练。本文通过四歩相移共采集29 人，每人除去大拇指和小拇指共6 根手指，每根手指各采集3次，共采集得到522 组数据。这522 组指纹条纹图像采集方式为四步相移，即每个频率有四个不同相移图像，这样也便可以获得2 088 组高频指纹条纹图与相对应的包裹相位图，图像像素大小为480×640，其中2 000 组作为网络训练集，剩余88 组作为测试集进行网络模型质量评估，图2是部分采集得到的条纹图与对应相位图的展示，其中能观测到清晰的指纹信息。

图2 指纹条纹图像示例Fig.2 Fringe pattern examples of fingerprints

2 基于卷积网络的相位提取

2.1 网络模型介绍

针对三维指纹测量中的单幅条纹图相位提取问题，本文的卷积神经网络框架是基于卷积神经网络（Convolutional Neural Networks，CNN）搭建的，由编码器、残差模块和解码器三部分组成，图3是简化后的网络结构示意图，每一层的网络具体参数在表1中给出。

图3 网络结构图Fig.3 Network structure

表1 神经网络各层的参数Table 1 The parameters of each layer of the neural network

在网络结构的设计中，首先考虑数据输入的问题。由于手指指纹细节具有很细微的特征，归一化操作将会丢失指纹细节特征，这是三维指纹采集所不能够接受的，因此直接以图像像素值大小为0 到255 范围进行网络输入。编码器主要由卷积层所组成，卷积层旨在通过卷积操作实现对图像局部细节的感知，并在一定程度上降低噪声的干扰。卷积层中图像通道数则取决于卷积滤波器（内核）的数量。一般来说，使用的过滤器越多，网络估计就越准确。然而，使用更多过滤器也意味着更多的训练时间，为了平衡网络性能和效率，第一层卷积层过滤器的数量设置为64，之后两层卷积层过滤器数量分别为前一层的两倍，分别为128 和256。由于指纹条纹图像绝大部分为背景，因此第一层过滤器的大小设置为7×7，步长设置为1，而之后的两个卷积层过滤器大小设置为3×3，步长为2。在卷积层之后，本文设计加上了九个残差块，每个残差块包含两个卷积层。残差块的加入加快网络训练阶段的收敛速度，从而提升网络训练效率。在残差块之后，采用三个反卷积用于将多尺度数据返回到原始维度。整个网络结构使用Relu 激活函数，来实现网络线性函数到非线性函数的转换，从而加强神经网络表达能力。

2.2 损失函数

损失函数用于评估预测值与真实值之间的差异。神经网络模型的训练旨在最小化预期损失，因而损失函数的设置至关重要。现有基于神经网络直接对相位进行提取的算法中，损失函数往往是真实值与预测值之间的L1 或L2 距离。这是经典的神经网络损失函数的设置。然而在包裹相位提取中，由于包裹相位在2π处存在骤变，对于相位来说，小误差会造成该区域出现较大的损失值，从而造成网络优化的不确定性，从而在之后的三维重建中产生较大的误差。为了有效解决指纹包裹相位图像2π 间断处预测质量偏差的问题，本文提出了一种新的混合损失函数，如式（6）所示。

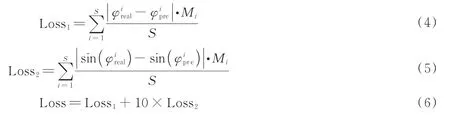
式中，φreal表示相位真值，即传统算法四歩相移得出的结果，φpre表示本文设计的神经网络预测出来的结果，Mi表示在1.1 节中提取得到的指纹感兴趣区域掩膜，S表示指纹感兴趣区域面积像素数量。在网络进行损失函数计算过程中，将提取得到的感兴趣区域分别与真值和预测值进行点乘的操作去除背景干扰之后计算损失，从而实现只是针对指纹感兴趣区域进行损失函数的计算。考虑到Loss2是正弦函数其值相比于Loss1会过小而易被网络所忽视，因此有必要对该部分损失加上权重。同时经分析可得，刚开始网络训练注意力应主要集中于间断区域以外之处，如将权重设置过大，会将网络的注意力过度集中于间断区域，而忽视指纹细节。本文结合实验对比权重5，10，15，20，最终将Loss2权重设置为10。

为了体现Loss2的效果，本文模拟了两张相差0.01π 的包裹相位图。图4（a）为这两张第200 行的包裹相位值。接着对这两张模拟包裹相位图像分别进行式（4）与式（5），即Loss1和Loss2的计算，为了更加直观地观察，本文同样选取第200 行的结果进行展示，Loss1和Loss2的结果分别如图4（b）所示，通过图像观察，在应用Loss2之后有效降低了包裹相位2π 处因存在骤变而所带来急剧的误差影响，从而将网络注意力更多的集中于包裹相位的质量，提高网络对指纹包裹相位预测的精度。

图4 模拟包裹相位图Fig.4 Wrapped phase simulation

3 实验结果与分析

3.1 相位提取结果对比

为验证本文提出的基于神经网络相位提取方法结果的可靠性和优势，本文使用传统方法包括傅里叶变化（Fourier Transform，FT）［31］和加窗傅里叶变化（Window Fourier Transform，WFT）［32］，神经网络方法包括HU［26］和FENG［18］神经网络对采集获取得到的指纹数据集进行相位提取，并对其结果与本文提出的方法进行比较，其结果如图5所示。

图5 不同相位提取方法结果及局部效果展示Fig.5 Phase extraction results and corresponding local effect demonstration

在图5中展示的实验结果中，第一行为常规四歩相移得 到的相位提取结果，第二行 为傅里叶变化得到的相位提取结果，第三行为加窗 傅里叶变化相移得到的相位 提取结果，第四行为应用HU 得到的结果，第五行为应用FENG 得到的结果，第六行则为本文提出的方 法结果，第二列和第四列分 别为左侧图像局部细节展示。对比常规四歩相移结果，首先可以看出这五种相位提取方法在手指大致结构有着较好的预测表现。在指纹特征方面，由于指纹的脊谷纹路跟条纹具有相似性［33-34］，从图5（b）与5（c）的局部放大图可以看出，傅里叶变化与加窗傅里叶变化在指纹特征处根据指纹纹路进行相位提取，可以观察到清晰的缠绕相位变化，这明显与相移法结果不同，不利于之后的三维重建。而HU 的方法与FENG 的方法对比本文的方法，整体观察与常规四歩相移算法差距不是很明显，通过进一步分析指纹局部细节信息，特别放大2π 间断处局部特征，可以明显观察到本文提出的算法在指纹三维测量的这些突变区域的关键指纹细节上保留的更加完整，指纹细节纹路也是连贯且清晰可见的。因此，通过观察对比包括本文在内的五种相位提取方法，可以得出本文提出的基于神经网络相位提取方法有着更加不错的表现。

为进一步对比两者差距，以常规四歩相移算法作为真值，用这三种方法分别应用平均绝对误差（Mean Absolute Error，MAE）进行误差计算，计算误差范围均为指纹感兴趣区域，即不包含背景区域。同时为了规避单张图像存在的偶然性，误差测试是面向测试集共88 张手指相位图然后得出的平均值，结果如表2所示。指纹包裹相位图像的像素值范围为［0，2π］，如表2所示，傅里叶方法误差为0.394 7，加窗傅里叶变化误差为0.341 7，应用HU 的神经网络方法误差为0.165 1，应用FENG 的方法误差则为0.179 2，而本文提出的神经网络误差为0.083 9，因此从指标上来看也是验证了上述通过观察得出的结论，本文提出的神经网络相位提取方法同样有着更加好的表现，预测结果更加接近传统四歩相移算法结果。

表2 相位提取精度对比Table 2 Comparison of phase extraction accuracy

本文将图5中HU、FENG 方法与本文方法获取的图像进行进一步结果对比，如图6选取三种相位提取结果的200 行与四歩相移第200 行更进一步细节结果比对，三行图像分别对应本文的算法、HU 和FENG 方法。其中带‘x’线为四歩相移结果，带‘o’线为本文应用神经网络相位提取算法后预测得到的结果，不难观察到本文提出的算法对比HU 方法重合度是更高的，由于FENG 方法是预测反正切函数的分子与分母使得其在间断区域保持了较高的精度，与本文方法的结果精度也是相近的。需要注意的是，包裹相位图像2π 间断处是神经网络预测的难点，从图中也可以看出本文算法在该区域能有较好的表现，这验证了本文应用的两个损失函数是可靠的，因此得到包裹相位结果有着较好的效果表现。

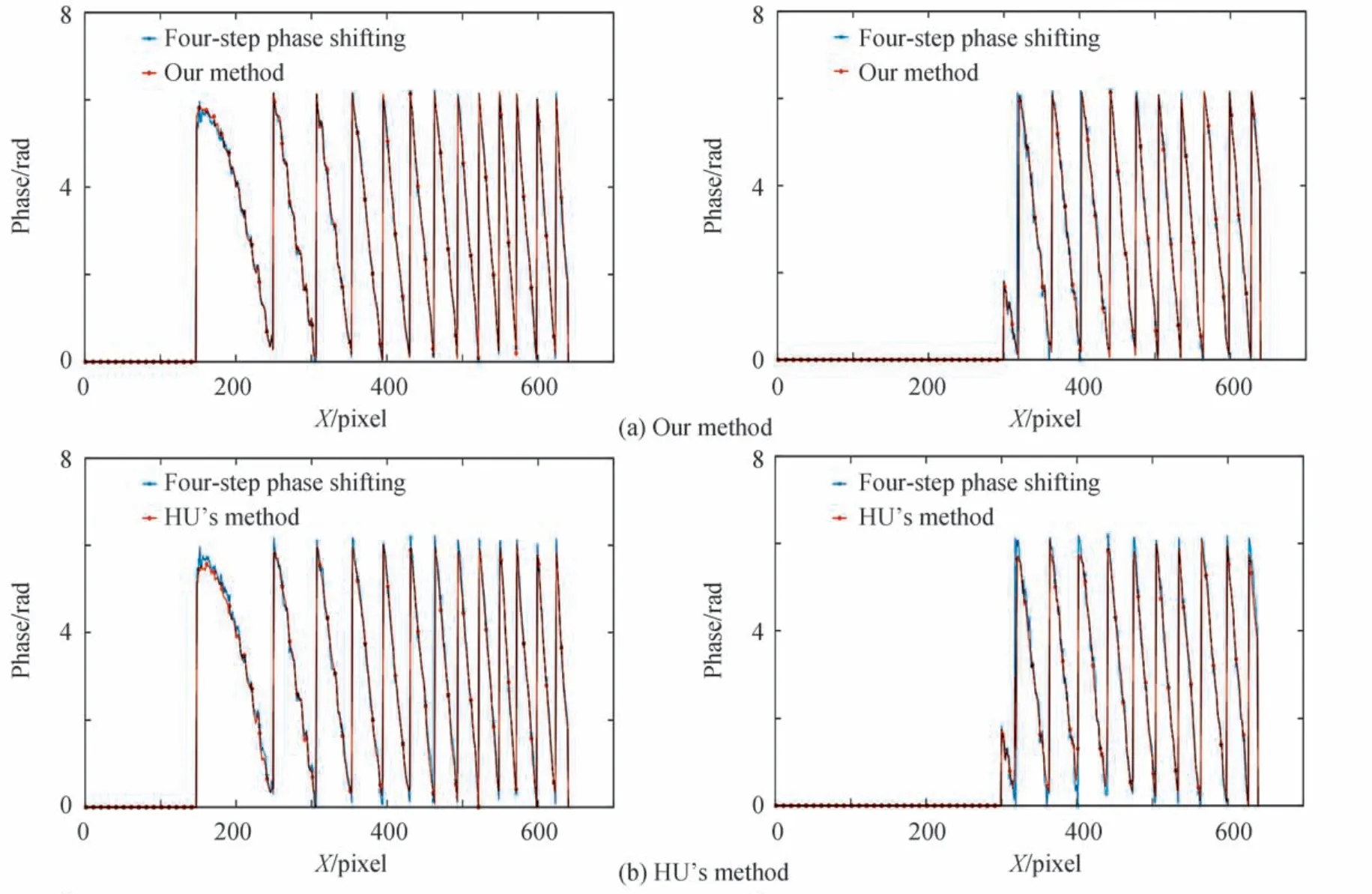
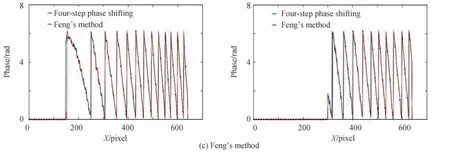
图6 两张不同手指相位图像第200 行精度结果展示Fig.6 Phase demonstration of the 200th line of two different fingers

3.2 包裹相位间断处误差对比

在损失函数评价中，本文为约束指纹包裹相位图2π 间断处误差设计了式（5）的正弦损失函数，为了评估包裹相位图像在间断处的质量本文进行了误差计算。如图7（a）首先通过差分方法突出指纹包裹相位图像间断处特征，再通过二值化法使得变为纯黑和纯白两种颜色的图像如图7（b）所示，考虑到实际间断处范围会稍大于由此得到的区域，因此通过膨胀算法将间断区域进行扩张，得到结果如图7（c）所示的包裹相位图2π 间断处区域后，应用点乘操作分别得到FT、WFT、HU、FENG 和本文算法在该区域的误差进行对比，结果如表3所示，可以发现本文网络在指纹相位提取方面有着明显的优势，证明了本文提出的正弦损失函数能在一定程度上提升神经网络在包裹相位2π 间断处的预测误差。

图7 包裹相位图2π 间断处提取Fig.7 The 2π discontinuity region extraction of wrapped phase map

表3 包裹相位间断处误差展示Table 3 Phase errors at the 2π discontinuity region

3.3 图像相似度实验

图像在神经网络处理过程中都有可能存在失真的问题，因此有必要对本文算法得到的结果进行相似度评价，本文选取了两种指标进行客观评价网络预测的结果，分别为结构相似度（Structural Similarity Index，SSIM）和直方图相似度（Histogram similarity），结构相似度是根据图像的亮度与对比度进行综合计算，而直方图相似度顾名思义是通过两张图像直方图进行相似度对比，两种指标都是越接近1 就代表越相似，结果如表4所示，本文算法得到的结果其结构相似度和直方图相似度结果分别为0.980 7 和0.866 1，体现了本文构建的神经网络得到的包裹相位图像具有较高的质量。

表4 图像相似度结果展示Table 4 Image similarity results

3.4 不同损失函数性能比较

在构建完神经网络框架后，本文对不同损失函数下的网络预测结果进行了对比，包括均方误差（Mean Squared Error，MSE）、Loss1与Loss。同样采用整体误差和2π 间断区域误差进行对比，如表5和表6所示。包裹相位误差中，使用MSE 误差为0.157 8，仅使用Loss1误差为0.084 7，应用本文损失函数，即使用Loss 的综合误差为0.083 9。包裹相位2π 间断区域，使用MSE 误差为0.206 1，仅使用Loss1误差为0.120 9，使用Loss 的误差为0.104 9。

表5 不同损失下包裹相位误差Table 5 Phase errors under different losses

表6 不同损失下包裹相位间断处误差Table 6 Phase errors at the 2π discontinuity region under different losses

因此可以得出网络预测结果在使用L1 距离作为损失函数计算会明显优于使用L2 距离作为损失函数。如图8所示，以MSE 为损失函数可以观察到在2π 间断处指纹存在信息丢失的问题。本文应用综合损失不仅能在相位缠绕处提升预测精度，也可以在整体上提升网络对包裹相位的预测精度。

图8 不同损失函数结果Fig.8 Display of different loss function results

3.5 连续相位结果对比

在上述相位提取的基础上，本文对提取得到的包裹相位进行解缠，如图9所示，其中第一行是常规四步相移法解缠后的绝对相位，第二行是相对应手指在本文神经网络相位提取算法后解缠获取得到的绝对相位，第三行与第四行为对应的连续相位图第200 行进行局部细节比对结果，带‘x’线为四歩相移结果，带‘o’线为本文算法预测得到的结果。从图（9）可以看出，本文提出的方法在解缠获取得到绝对相位仍具备较高的质量。

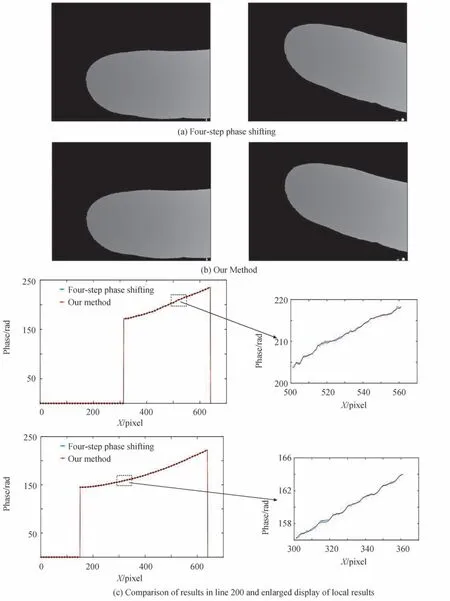
图9 相位解缠结果及第200 行相位解缠精度展示Fig.9 Demonstration of phase unwrapping results

不论从整体绝对相位实验结果展示，还是从具体第200 行局部对比结果展示，都可以看出本文提出的基于神经网络相位提取方法所具有较好的效果，与作为真值的常规四步相移算法差距不大，进一步证明了本文提出的基于神经网络相位提取方法的可靠性。

3.6 三维重建结果展示

本文对应用常规四歩相移算法、HU、FENG 与本文算法重建的三维指纹进行展示，进一步验证本文提出的基于神经网络的相位提取算法的效果。为了更好地展示效果，指纹点云皆通过Geomagic Studio 12 软件建模。图10展示了两根手指的三维手指结果，其中第一列是四步相移法得到的三维重建结果，第二列是对应的手指在HU 方法得到的三维重建结果，第三列为应用FENG 方法得到的三维重建结果，第四列为应用本文方法得到的三维重建结果，从图10可以看出，使用本文方法获取的指纹脉络清晰、脊谷分明，特别是在包裹相位2π 间断区域有着较好的表现。

图10 基于Geomatic Studio 12 的三维结果Fig.10 3D results based on Geomatic Studio 12

4 结论

针对非接触三维指纹测量，本文对三维指纹采集系统搭建和应用神经网络进行指纹相位提取展开研究。搭建了基于条纹投影技术的三维指纹采集系统，经过Gamma 误差校正、指纹有效区域提取，获取指纹条纹图像。之后对采集得到的条纹图构建卷积神经网络，针对如今主流的相位提取神经网络中包裹相位2π间断处误差剧增难优化问题，构建了新的包裹感知的损失函数对该区域进行约束，从而提高网络在2π 间断区域预测的准确性。经过实验与对比表明，本文所提的方法在三维指纹测量领域，单幅条纹图的相位提取方面有着较好的表现。