基于降采样粒子群优化的子孔径拼接干涉方法
2022-07-27王若言朱丹袁群刘威剑高志山
王若言,朱丹,袁群,刘威剑,高志山
(南京理工大学 电子工程与光电技术学院,南京 210094)
0 引言
干涉检测是一种非接触式的检测技术,它可以高精度地获取测试元件的表面信息,已广泛用于工业、医学和天文学等领域[1]。近些年来,大口径光学系统在各领域的需求不断增长,针对这类系统中大口径光学元件的检测,目前较为传统的方法是利用与被测件口径相当的大口径干涉仪,直接完成全口径面形检测。这种方法检测精度高且测试过程简单,但是大口径干涉仪价格昂贵且制造难度大。为了摆脱大口径样品检测对干涉仪尺寸的依赖,利用常见尺寸的干涉仪完成大口径样品的检测,用子孔径拼接干涉检测技术来获得大口径光学元件的完整面形图。子孔径拼接检测方法由KIM C J[2-3]于1982年首次提出,被测部件的全口径被划分为多个子孔径,分别对每个子孔径进行干涉检测,然后拼接所有子孔径的面形图,以获得全孔径面形参数。在对不同子孔径检测的过程中,为了更准确地获得每个子孔径的面形数据,需要对待测镜面的位置进行微调,因此会引入调整误差。调整误差包括相对z轴的平移,相对x、y轴方向的倾斜等,这些误差都是不可忽略的。同时受限于机械位移装置的定位精度和直线度,在对不同子孔径扫描过程中,相邻子孔径的实际位置偏差会与机械扫描装置的名义位移量不一致,即在扫描过程中引入了定位误差。机械扫描引起的定位误差将导致两个相邻子孔径重叠区域中的对应点不匹配,从而严重降低检测精度。在机械定位精度不高的情况下,提高拼接的精度和速度成了拼接干涉检测研究的主要方向。子孔径拼接检测中,通过每个子孔径中离散点的相位信息来描述获得的面形数据。每个子孔径面形图不仅包含被测子孔径的实际面形,还包含参考表面面形误差、调整误差和定位误差。由于干涉仪所用的标准透射平面或球面的面形质量很高,因此可以忽略参考面面形误差。由平移、倾斜和离焦等因素引起的调整误差一般可以通过最小二乘法进行拟合校正[4]。在机械定位精度不高的情况下,为了尽可能提高定位精度,消除定位误差,研究人员提出了一些辅助定位措施[5-6]。MAURER R 等[7]提出标记点法,在样品表面人为标记多个点,通过对准标记点的位置来实现子孔径测试数据的匹配。ZHANG P 等[8]提出立体视觉法,使用两个相机同时对机械位移装置上的标记点进行成像,然后计算标记的位置以实现子孔径的准确定位。
辅助定位的方法提高了定位精度,但增加了额外的运算量,降低了子孔径拼接检测的效率。因此,越来越多的研究小组利用高效的优化算法完成对定位误差的求解。TANG S 等[9]在考虑了刚体运动六个自由度的前提下,通过拟合重叠区域的面形偏差获得了最佳的定位误差估计。SJŐEDAHL M 等[10]提出了一种迭代算法,用以计算六个自由度的最佳估计值,而后更新重叠区域数据,直到算法收敛到预设的精度。陈善勇等[11]将子孔径数据转换至三维全局坐标系中,优化了子孔径与重叠区域对应点对之间的位姿关系。目前对于定位误差的求解一般以满足整像素的定位精度为目标[12-14],但是随着对于面形测量准确度要求的不断提高,不少研究小组开展了亚像素量级的定位误差求解方法研究[15]。
迭代算法通过交替优化的方式使得定位误差和调整误差依次收敛,但由于两者之间存在相互耦合,这种交替优化的方式并不能准确解析两种误差间的关系。为了实现定位误差和调整误差的同时校正,在美国QED 公司研发的子孔径拼接干涉仪中,采用迭代的全局优化算法[16-17],同时修正了机械定位误差和调整误差。另外卢炳辉等[18]提出了基于映射图像匹配的子孔径拼接方法,将形貌旋转关系转化为图像坐标的平移关系,再利用图像匹配算法得出子孔径坐标系间的对应关系。此外,一些搜索算法通过全局优化方法,也可以实现两种误差的同步优化。陈一巍[19]将遗传算法引入到子孔径拼接中,避免了在求解定位误差和调整误差时陷入局部最优解,对定位误差大于一个像素的情况,具有很好的补偿效果。上述三种实现定位误差和调整误差同时修正的方法,虽然在很大程度上降低了拼接误差,提高了面形检测精度,但是普遍存在算法构建复杂、运算量大、拼接效率低下等问题。在拼接检测过程中,除去干涉条纹调零过程中产生的调整误差外,还在拼接扫描过程中引入了定位误差,两种误差之间相耦合。需要通过合适的优化算法,对各个子孔径相对基准子孔径的调整误差和定位误差同时进行搜索补偿,对于这种多参数优化问题,粒子群优化算法[20]是一种很好的选择。粒子群优化是一种通过模拟鸟觅食行为发展出来的随机搜索算法。该算法模型参数设置简单,可被运用到高精度子孔径拼接定位中。朱峰等[21]将粒子群算法运用到柱面镜拼接中,优化搜索全部子孔径的定位误差,完成子孔径的同步拼接。陈一巍等[19]通过粒子群算法对图像锐化后的子孔径面形进行机械定位补偿,避免搜索时陷入局部最优解,实现错位情况下子孔径的定位。目前子孔径拼接技术中使用的粒子群优化方法大多仅以定位误差为优化目标,未能充分利用粒子群算法全局优化的优势,准确解析定位误差和调整误差之间的关系。并且现有文献均直接对原始面形数据进行粒子群优化,算法搜索耗时较长。为了提升全局优化搜索效率,本文提出了一种基于降采样粒子群优化的子孔径拼接算法,将定位误差和调整误差同时作为粒子群算法的优化对象,并通过对各子孔径面形数据的降采样处理减少搜索数据量,在粗配准结果基础上,结合原始未降采样数据,运用梯度算法得到准确拼接结果。
1 基本原理
1.1 子孔径拼接的定位和调整的误差
为了完成子孔径拼接检测,需要利用最小二乘法实现相邻子孔径的面形拼接。如图1所示,以两个相邻的子孔径w1和w2为例,它们在x和y方向存在着Δx和Δy的相对位移,且两个子孔径间在全局坐标系中,对应的俯仰倾斜也不相同。分别定义两个相邻子孔径中的重叠区域为w11和w22,它们对应实际测量中被测镜上的同一块区域。由于两个子孔径间存在相对调整误差,利用最小二乘法使得重叠区域对应点的距离最小,从而完成两个子孔径面形的拼接,即
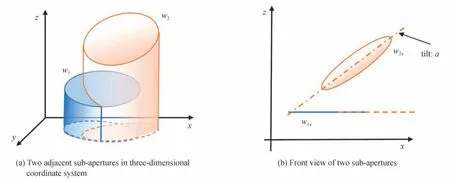

图1 全局坐标系内两个相邻子孔径的拼接示意图Fig.1 Stitching model of two adjacent sub-apertures in global coordinate

式中,a和b分别为待求解的俯仰和倾斜系数,c为待求解的相对平移量。
在理想情况下,Δx和Δy对应着位移平台的名义位移值。然而,在实际检测过程中,由于机械位移平台位移过程中不可避免的定位误差(dx,dy),则式(1)中需要额外引入两个定位误差变量,即改写为

因此,为了完成相邻子孔径的准确拼接,除了求解相对调整误差对应的系数a、b、c以外,定位误差dx、dy的值也需要得到精确的求解。
1.2 降采样粒子群算法的构建
粒子群算法[20]的基本思想源于对鸟群觅食行为的研究。算法中,每个待优化问题的解都可以看作一个“粒子”。根据待优化的目标函数,可以计算每个粒子的适应度,通过比较目前的适应度以及种群历史最优适应度,可以完成“粒子”在解空间的最优搜索。在子孔径拼接检测中,将重叠区域对应点的最小二乘距离设为所需优化的目标函数。待搜索粒子最佳位置包括:子孔径间的定位误差dx、dy,子孔径的相对装调误差如平移、俯仰、倾斜等多个变量。此外,为了保证拼接的准确性,重叠区域内的像素数普遍较多。因此,如果选择对原始的图像进行粒子群优化,则算法耗时较长。在本文中,对重叠区域内的面形数据进行降采样,大大提高粒子群优化算法的速度,具体算法过程如下:
假设在K维系数搜索空间,其中K由子孔径间的定位误差dx、dy,子孔径的相对装调误差如平移、俯仰、倾斜等变量个数决定,选择N个粒子构成一个种群,其中第i个粒子表示一个K维向量,Xi为第i个粒子的取值,即

令第i个粒子的移动速度也是一个K维向量,则有

对于降采样后的面形数据,首先对粒子群进行初始化,设置目标函数的自变量个数,在速度区间和搜索空间上随机初始化速度和位置。
随后,根据优化的目标函数(重叠区域对应点的最小二乘距离)计算每个粒子的适应度。
接着,对于每一个粒子,比较其当前的适应度以及历史最好适应度,选择更优的适应度进行更新。
为了防止定位误差和装调误差各项之间出现耦合作用,分别考虑个体最优解和全局最优解。经过第d次迭代,假设第i个粒子目前搜索到的历史最好位置为Xi_b,则称该位置为个体最优解Pid,即

全局最优解Pgd表示整个粒子群的历史最好位置,即从所有个体最优解(P1d,P2d,...,PNd)中选择适应度最好的位置,令

利用获得粒子的个体最优解和全部粒子的全局最优解来更新每个粒子的速度V和位置X,即

式中,ω为惯性权重,C1和C2称为学习因子或加速系数,r1和r2表示区间[0,1]内的两个随机数。
在经过粒子群优化算法后,获得降采样面形数据中对应的定位误差以及装调误差系数,该系数可以作为两个全采样原始子孔径面形数据的粗略预估值。在粗定位的基础上,结合原始的面形数据,通过梯度算法计算精定位。假设粗定位后两个子孔径重叠区域仍然存在(δx,δy)的偏差,分别用f(x,y)和g(x+δx,y+δy)来表示两个重叠区域,则二者的关系可表示为

为了求解(δx,δy),可将式(9)改写为


基于降采样粒子群优化的快速子孔径拼接方法流程如图2所示。
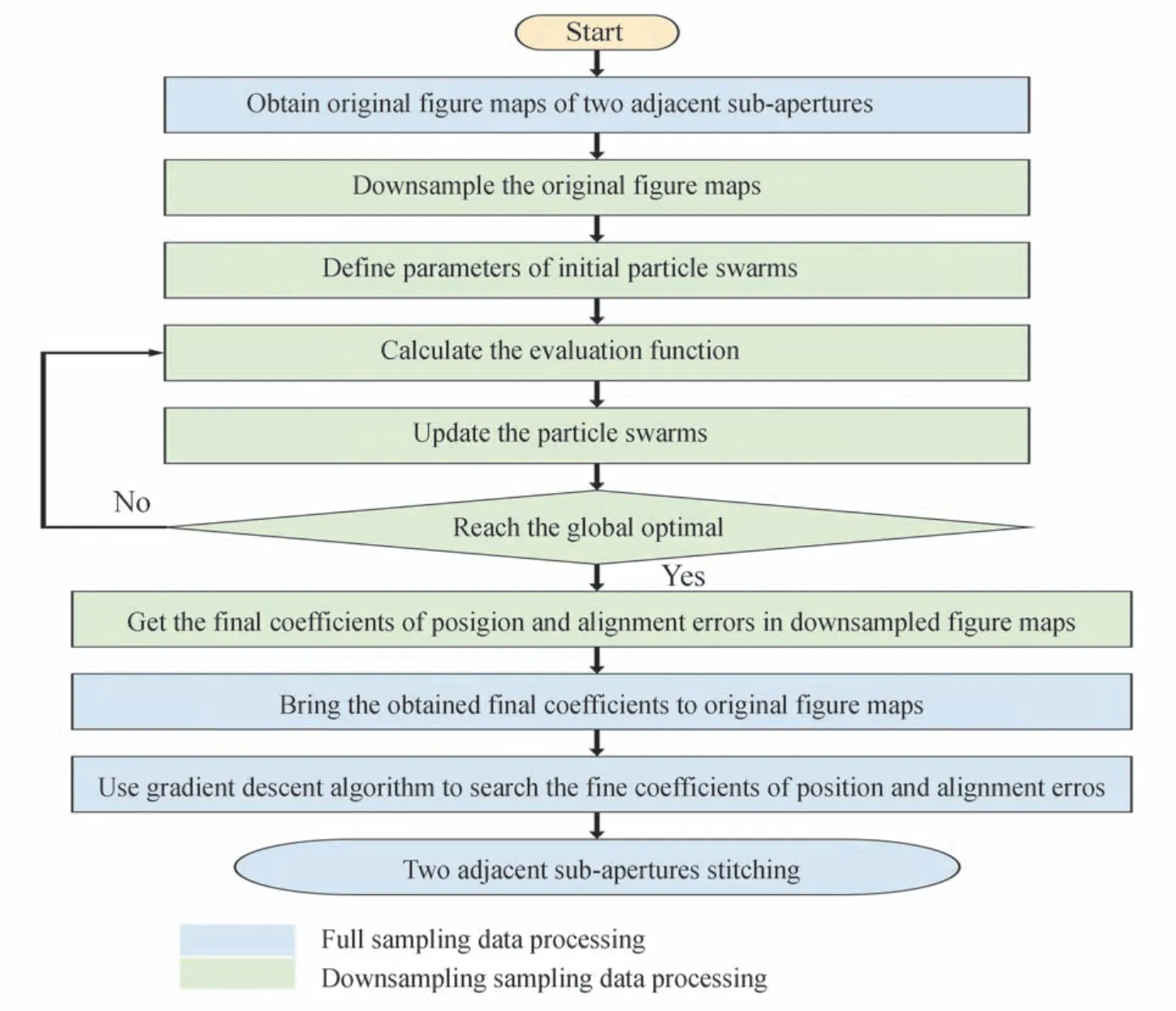
图2 基于降采样粒子群优化算法的子孔径拼接方法流程Fig.2 Flowchart of sub-aperture stitching based on down-sampling particle swarm optimization algorithm
以1 000×1 000 像素的面形采样数据为例,将像素数划分成4×4 的小格,对其取平均,得到250×250 的降采样面形数据。通过对减少1/16 的像素数进行粒子群搜索,将大大减少算法的运行时间。
2 模拟仿真分析
首先在模拟的两个相邻子孔径上对提出的降采样粒子群优化算法进行验证。将Zygo 干涉仪获取的球面镜面形数据作为子孔径的原始数据,如图3(a)所示。重叠区域的选择在图(b)中表示出,灰色圆表示原始的面形数据,蓝色和橙色圆圈表示子孔径w1和w2。

图3 算法仿真用球面镜原始面形Fig.3 Surface map of spherical mirror for simulation analysis
为了更准确地模拟实际的检测过程,需要人为地对两个子孔径面形图引入一些误差。首先,引入随机高斯噪声([−0.000 2,0.000 2]λ)以模拟不同孔径检测的随机误差。然后,在合理范围内对各个子孔径,分别加入由相对倾斜和相对轴向平移所引起的面形误差。此外,由于被测样品为球面镜,还要额外引入离焦项。最终面形误差的表达式为a(x2+y2)+bx+cy+d,仅对于本文所提的降采样粒子群算法而言,a、b、c、d可以取任意值,但是由于本文仿真所用球面镜数据,实际两个相邻子孔径的相对调整误差并不会无限大。因此,为了更准确地模拟实际子孔径面形,对a、b、c、d取值范围进行约束,保证离焦项小于0.32λ,x和y的倾斜小于0.2λ,相对轴向位移小于0.05λ,即a∈[-0.000 002,0.000 002]λ,b,c∈[-0.000 5,0.000 5]λ,d∈[-0.05,0.05]λ。最后,在各个子孔径引入随机的相对定位误差,使其满足dx,dy∈[-20,20]像素。
对得到的随机面形数据,通过粒子群算法获取相邻子孔径间的准确定位,并消除调整误差。本文算法中,随机生成20 个粒子,惯性权重ω设定为1,学习因子C1主要控制个体最优解对更新迭代步长的影响,学习因子C2主要体现全局最优解对寻求解值的影响,两者皆设定为2,迭代次数设为20 次。在粒子群算法迭代过程中,相邻子孔径重叠区域内对应点的最小二乘距离变化如图4(a),在经过6 次迭代后,模型已经达到全局最优解,且算法获得的面形误差表达式也与预设误差相一致。为了验证面形复原的精度,计算重叠区域处复原面形与原始面形数据之间的残差,结果如图4(b)所示,残差的峰谷值(Peak Valley,PV)为9.9×10-5λ,均方根(Root Mean Square,RMS)为2.89×10-5λ,主要为随机噪声引起。

图4 粒子群算法优化结果Fig.4 Results after particle swarm optimization
为了提高粒子群算法的计算速度,采用降采样的方法,减少子孔径面形中的数据点,利用粒子群算法获取子孔径之间的粗定位,得到降采样后的搜索结果,再将该结果带入到子孔径的原始数据中。粗定位结果和实际情况相比会有两个像素以内的偏差,两子孔径重叠区域与原始面形数据的残差如图5(a)所示,此时残差的PV 为0.182 0λ,RMS 为0.003 2λ。为了获得准确的子孔径定位,根据当前的粗定位结果,进一步运用梯度法对子孔径的定位偏差进行精确调整,得到准确结果后,用最小二乘法消除调整误差从而完成拼接。最终得到的重叠区域与原始面形数据的残差结果如图5(b)所示,残差的PV 为9.9×10-5λ,RMS 为2.89×10-5λ,该结果与单纯粒子群算法的一致,证明了本文所提方法的准确性。
假设对一个NX×NY像素点的图像进行N阶降采样,则降采样后的图像尺寸为X×Y像素,代入粒子群算法运算的数据点减少了N2倍。在每一次迭代计算单个粒子的适应度时,运算量与数据点数量有关,因此N阶降采样后的运算量也减小了N2倍。执行粒子群搜索运算时,在搜索粒子数量和搜索步长不变的情况下,如果迭代循环次数相仿,可以使得算法运算速度加快约N2倍。本文方法相较于单纯的粒子群优化方法增加了降采样运算和单次的梯度运算,运算时间远小于粒子群搜素算法的用时。分析可知,随着降采样阶数的提高,降采样后的数据运算量显著减小,算法运算速度也会显著提升。然而,越高的降采样阶数意味着降采样后每个像素位置包含更多的面形信息,使得粗定位的分辨率下降。较低的粗定位分辨率会导致后续精确定位的梯度算法陷入局部最优解。因此,为了综合考量降采样阶数对拼接精度和速度的影响,随机生成10 组不同误差的800×800 像素的面形数据,对每一组面形数据分别用不同降采样阶数的粒子群算法进行优化(20 个随机粒子,20 次迭代),统计其对应的平均运算时间,以算法准确定位次数,如表1所示。
由表1可知,随着降采样阶数的增大,10 次随机面形拼接的平均时间越来越短,但是随着阶数越大,每个降采样后像素内包含的面形信息越多,粗定位的分辨率也逐渐由2 阶的1 个像素,扩展到8 阶降采样时的4个像素,粒子群搜索的不准确度也增加。不准确度的增加会导致后期梯度法精定位时容易陷入局部最优解,即当6 阶降采样时,在10 次随机面形数据拼接中,只有8 次拼接是准确的,有2 次陷入了局部最优解。而随着阶数的不断提高,算法将更容易陷入局部最优解。因此,在综合考虑算法运行时间和面形复原精度的情况下,选择对面形数据进行4 阶降采样。由表中可知,单纯粒子群算法需要的时间为900 s,而通过4 阶降采样之后,本文算法的运算时间缩减为74 s,运算速度提高了约12 倍。

表1 不同降采样阶数对运行时间以及面形检测精度的影响Table 1 Influence of different down sampling order on running time and surface testing accuracy
3 实验结果
为了验证所提拼接算法的可行性,使用Zygo 干涉仪对4 英寸(1 英寸=2.54 cm)的平面镜进行测试,全口径检测面形如图6(b)所示,被测面形的PV 为0.036 3λ,RMS 为0.003 7λ。在标准参考平面后加入光阑,以模拟完成子孔径的检测,所有7 个子孔径的原始面形如图6(a)所示。运用所提方法对定位误差和调整误差进行校正,此时粒子群算法的参数设置与模拟仿真分析部分相同,随机粒子数为20 个,惯性权重ω为1,学习因子C1和C2均设定为2,迭代次数为20 次,降采样的阶数为4 阶,校正后面形如图6(c)所示,PV 值为0.036 4λ,RMS 为0.003 8λ。为了验证所提算法拼接的准确性,比较了本文方法与传统最小二乘法的拼接结果以及两种方法与全口径直接检测面形的残差,如图6(c)~(f)所示,本文所提方法的残差PV 为0.022 6λ,RMS 为9.53×10-4λ,明显优于传统最小二乘法的检测结果。
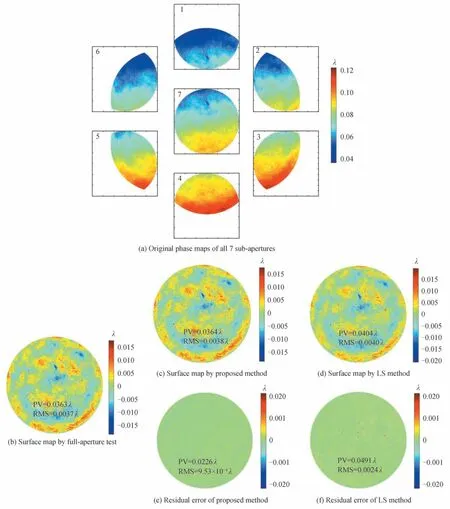
图6 4 英寸平面镜干涉检测结果Fig.6 Testing results of a 4-inch plane mirror
用Zygo 干涉仪对3 英寸的离轴抛物面镜进行测试。由于所用干涉仪的直径为4 英寸,大于检测的离轴抛物面反射镜口径,在干涉仪的出口处放置一个50 mm 的光阑,来模仿小口径干涉仪测试大口径镜面。整个光路遵循自准直的方法。如图7(a)所示,来自干涉仪的平行光束入射到离轴抛物面反射镜上,光被球面镜反射沿原路返回。

图7 离轴抛物面反射镜子孔径拼接干涉检测Fig.7 Testing of off-axis parabolic mirror by sub-aperture stitching interferometry
如图7(b)所示,将离轴抛物面镜划分为7 个子孔径,并通过五维位移机构实现对7 个子孔径的检测,其对应的面形如图8所示。

图8 离轴抛物面镜7 个子孔径面形图Fig.8 Surface maps of the 7 sub-apertures of tested off-axis parabolic mirror
由Zygo 干涉仪进行全孔径直接测试得到的表面如图9(a)所示,PV=2.652λ,RMS=0.352λ。利用提出的4 阶降采样拼接算法,算法参数设置与平面检测时保持一致,同时消除子孔径之间的定位误差、调整误差,拼接得到的全口径面形如图9(b)所示,PV 为2.635 7λ和RMS 为0.352 2λ。子孔径拼接干涉检测和全口径直接测试的残留误差如图9(d)所示,PV 值为0.181 9λ,RMS 值为0.012 2λ。图9(c)和(d)分别为最小二乘法求得的面形数据以及与全口径检测的残差值,由此可以发现,本文方法得到的面形数据与全孔径直接测试结果更加吻合。

图9 离轴抛物面镜面形检测结果Fig.9 Surface testing results of the parabolic mirror
4 结论
本文提出了一种基于降采样粒子群优化的快速子孔径干涉拼接方法,通过降采样的方式,加快了粒子群算法的搜索速度,获得相邻子孔径的粗定位,而后利用梯度算法获得子孔径的像素级定位,完成高精度的拼接检测。模拟仿真分析比较了本文算法与单纯粒子群搜索算法的速度优势,同时证明了本文算法拼接结果的准确性。为了验证所提算法的可行性,分别对大口径平面镜以及离轴抛物面反射镜进行了拼接检测,检测面形结果表明,与传统的最小二乘法相比,本文方法能够更准确地完成定位误差和调整误差的同步校正,面形检测结果与全口径直接检测结果更吻合。在后续的工作中,如果希望将定位精度提高到亚像素量级,可以先利用降采样粒子群优化方法获取粗定位之后,对面形数据进行插值,再运用梯度法获取子孔径的亚像素量级定位,实现更高精度的拼接检测。
