面向载荷运输的非锚定空间系留电梯轨道半径保持*

史格非

中山大学，广州 510275

0 引言

空间系留电梯(Partial Space Elevator，PSE)概念源于“航天之父”齐奥尔科夫斯基提出的“太空电梯”构想。其总体结构如图1。位于较高轨道的主航天器通过系绳将运输航天器系留于较低轨道，通过电力驱动电梯舱内部爬行机构，实现负载电梯舱沿系绳的快速移动。该系统构建灵活，运输成本低，安全性好，特别适于空间站物资运输及面向超大型航天器在轨组装的大范围跨轨道载荷交换。其相关技术拥有广阔的应用前景[1]。

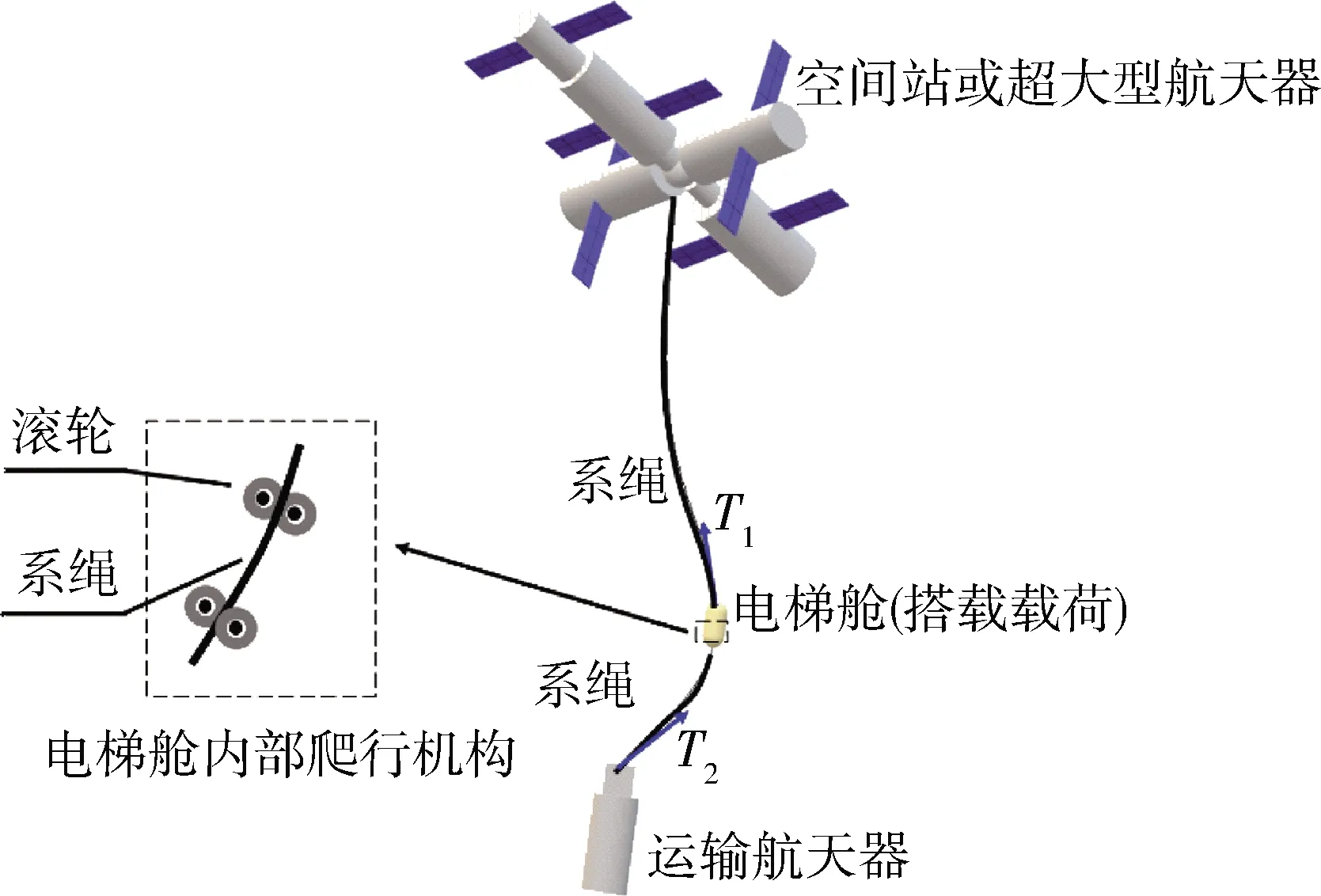
图1 空间系留电梯系统总体结构

在载荷运输过程中，系统各刚体间的动力学耦合将导致主航天器轨道参数发生变化，这不利于面向空间站及超大型航天器的货物运输。因此，如何将主航天器保持在目标轨道上，尤其是保持固定的轨道半径，是空间系留电梯面向货物运输工程实践的一个关键问题。

在过去的几十年里，许多学者都致力于空间系留电梯(PSE)的动力学和控制方法的研究。Misra等[2]和Lorenzini等[3]给出了空间系留电梯的数学模型。Cohen等[4]、Woo等[5]和Williams等[6]研究了PSE的动力学特性。Yamagiwa等[7]从工程角度研究了PSE。Kojima等[8]提出了“任务函数”控制方法，仅通过调整电梯舱移动速度来抑制货物运输过程中的系统摆动。史格非等[9]借鉴文献[10]，系统地研究了PSE的摆动动力学，提出了不使用推力的摆动抑制策略。进一步，文献[11]提出了一种控制非平衡欠驱动系统的“并行优化轨迹规划与跟踪”控制方法。上述工作皆假设主航天器锚定于固定轨道上。针对更为实际的情况，Jung等[12]建立了主航天器非锚定的PSE动力学模型，并对主航天器轨道半径的变化特性进行了初步分析，但相关问题依然有待进一步研究。到目前为止，对于非锚定PSE的轨道半径保持问题的研究非常有限，但依然可以借鉴部分现有的控制策略。钟睿和朱正宏[13]提出了一种分段最优控制方法来控制电动力绳系卫星系统的轨道参数和姿态。相关的优化方法可用于处理欠驱动空间多体系统，包括非锚定PSE。除了最优控制方法外，模糊控制也是控制PSE的一种可能方法。考虑到轨道和姿态控制的要求，Rao等[14]提出了一种基于模型预测控制的“三阶段”控制策略，用于对欠驱动绳系系统进行离轨控制。由于这种方法的泛用性和可实现性，可以考虑将其用于PSE的轨道保持及摆动抑制。

本文的研究目的是在不使用推力的情况下，实现对非锚定PSE在货物运输过程中主航天器的轨道半径保持。首先，扩展经典的“两哑铃模型”，建立空间系留电梯动力学模型。在平衡特性分析的基础上，提出了一种新的自稳定修正律。进一步，基于自稳定修正律，提出了一种新的控制策略并与SHMPC融合，在抑制系统摆动的同时，实现了主航天器轨道半径的保持。仿真结果表明，所提出的控制策略适应货物运输任务的特点，效果良好。

1 动力学建模与分析

非锚定空间系留电梯简图及状态参数如图2：

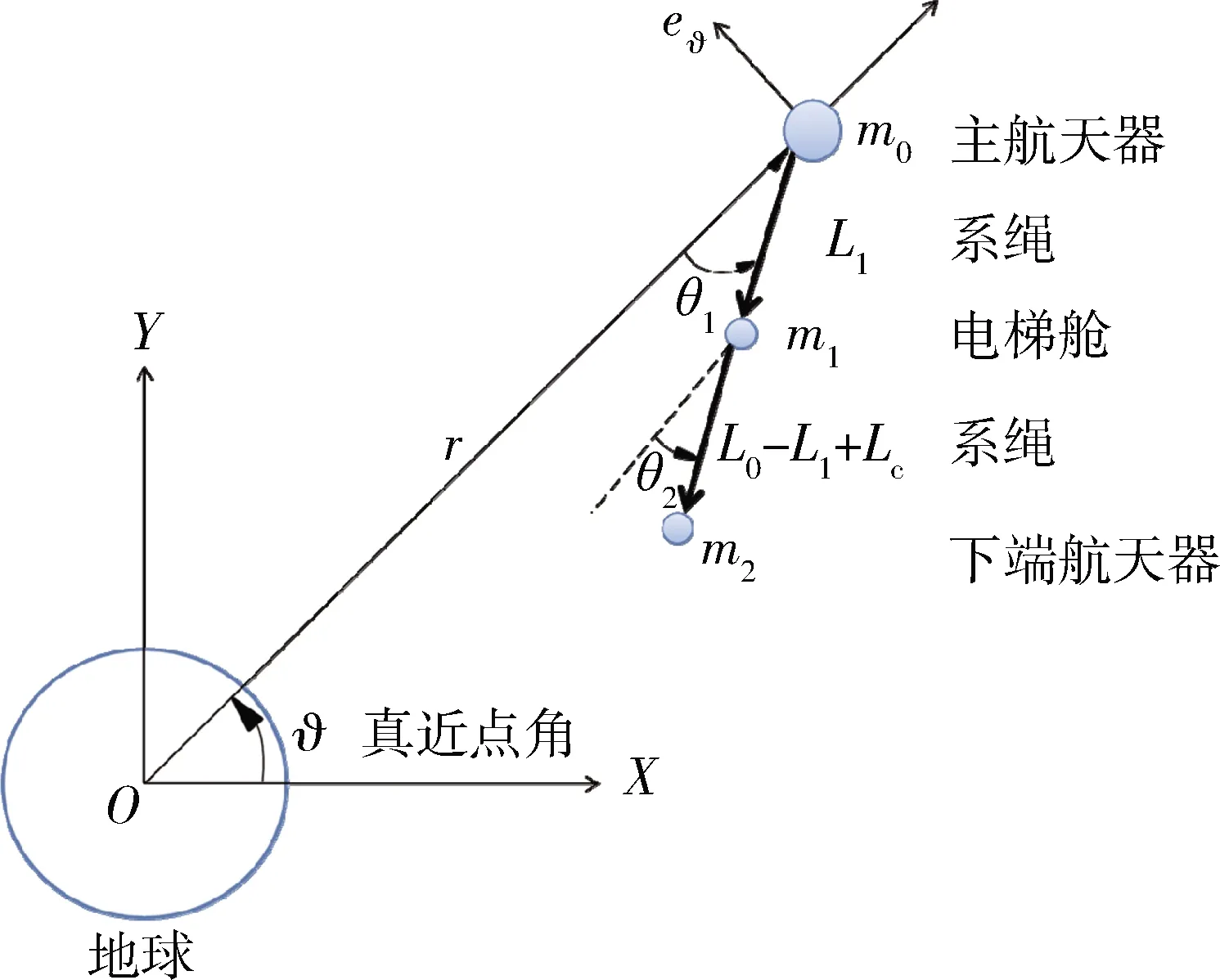
图2 系统简图及状态参数

为了简化模型，假设系统处于一个无扰动的中心引力场中，忽略大气阻力、太阳光压、面外运动、系绳质量和弹性[15]。动力学模型建立在地心惯性系O-XY中。采用拉格朗日方程建立系统动力学模型，得到系统的六自由度动力学方程：

(1)

(2)

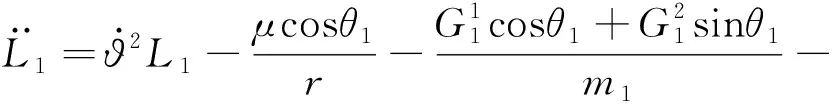
(3)

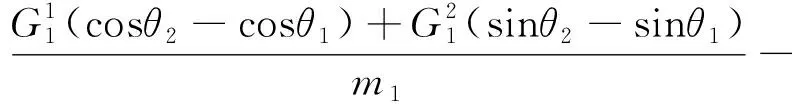
(4)

(5)

(6)

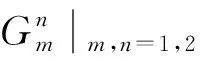
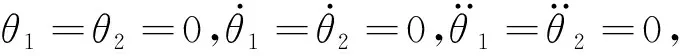
(7)

将式(7)代入系统动力学方程可以得到如下关系式：

(8)

(9)

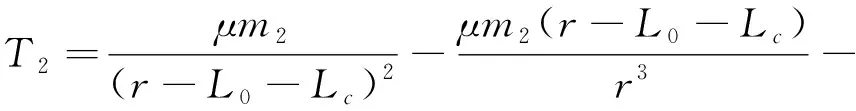
(10)

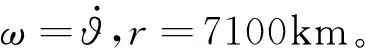
图3 轨道参数平衡状态

上述结果是基于系绳总长度不变的假设下得出的，即，Lc=0。在系绳总长度可变的条件下，对应不同的L1，可以得到特定轨道状态下的平衡解：

(11)

平衡点解集如图4中的实线表示。如图4(a)所示，对应不同的L1，可以通过改变Lc进行平衡，其变化范围为系统初始总绳长的45%～55%。在上述算例中，m1/m2=1/2，当该比值更小时，即电梯舱质量相比于下端系留飞船质量更小时，平衡解中的Lc减小，见图4(b)。

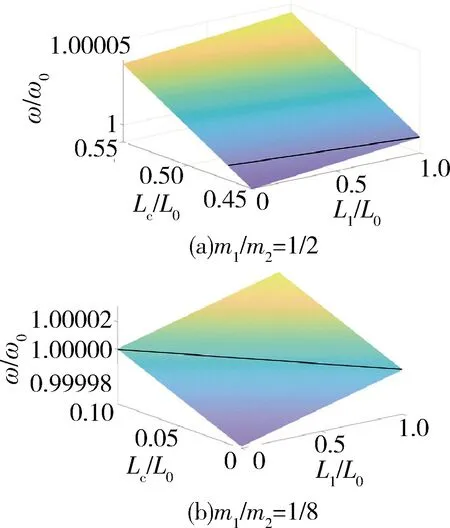
图4 对应固定轨道半径的平衡点轨道状态参数

综上所述，在平衡状态下，对应电梯舱不同的位置，r/r0的变化量远大于ω/ω0。此外，可以通过改变Lc，实现对非锚定的PSE的轨道保持，基于该结论，开展控制器设计研究。

2 控制器设计

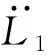
(12)

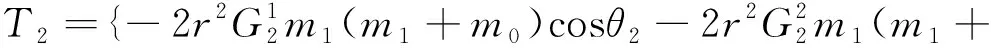
(13)

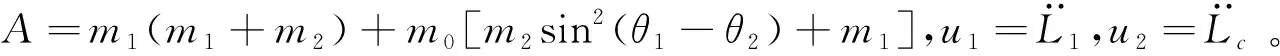
如式(5)所示，通过调节T1主航天器轨道进行保持的本质是对轨道半径动力学方程的修正。因此，可以以T1为虚拟控制输入，设计相应的修正律，实现主航天器轨道半径的自稳定。将该自稳定修正律写成滑模变结构控制律的形式，得到：

(14)

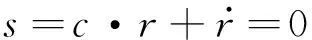
上述自稳定修正律可以看作是对控制输入的一种约束。在该种约束下，通过调节u1和u2，可以对主航天器轨道半径进行保持，并抑制非锚定PSE的摆动。由于货物运输是一个过程任务，故，要求系统状态在任务结束时收敛到平衡状态。对此，本文采用面向任务的SHMPC对系统进行控制。所预测的时域覆盖从当前状态到任务结束的时间段，控制时域则始终与预测时域成相同比例，当控制时域结束时，开始新的预测时域。本文忽略计算机运算时间。随着控制近程的推进，预测时域越来越短，相应的控制时域也在缩减，这意味着越是接近任务结束，控制步长及其对应的周期就越短，控制精度也越高，这可以极好地应对空间系留电梯运输任务所面临的“面条”效应[8]。当预测时域小于一个设定阈值时，其对应的控制时域直接与其相等，即控制进入最后一个周期。在本文中，考虑PSE的运输任务与系绳长度L1直接相关，因此控制时域直接以系绳长度作为尺度以代替时间尺度。这样，每个控制步长结束时刻tf是浮动的，则当前控制周期的目标函数为：

(15)

服从公式(1)、(2)、(5)、(6)、(13)、(14)以及

(16)

(17)

3 仿真校验

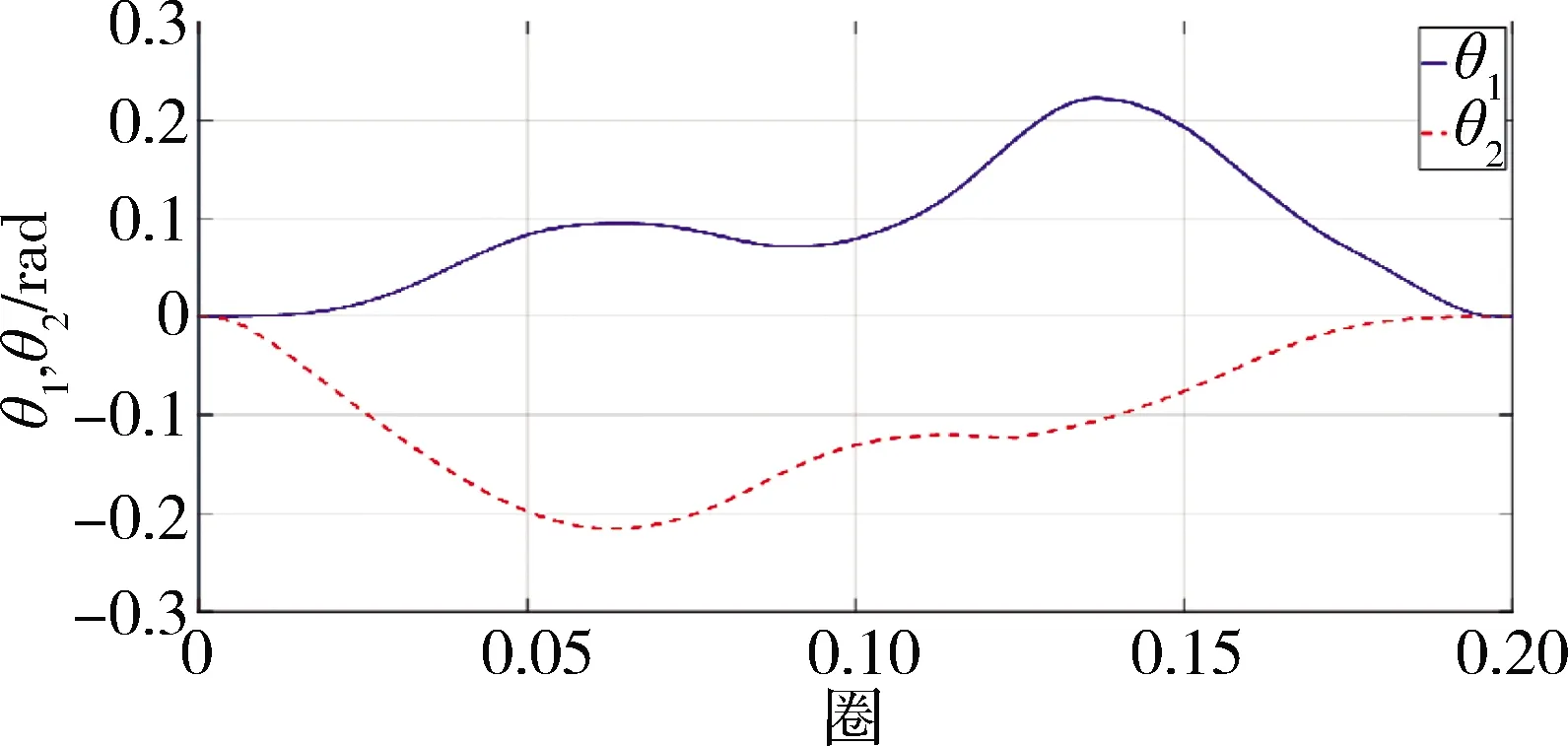
图5 系统摆角变化

图6 系绳长度变化

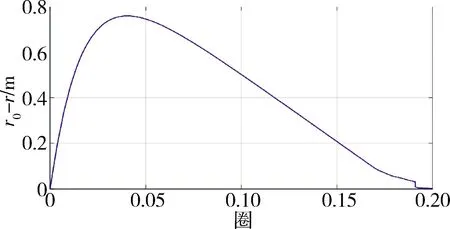
图7 主航天器轨道半径变化

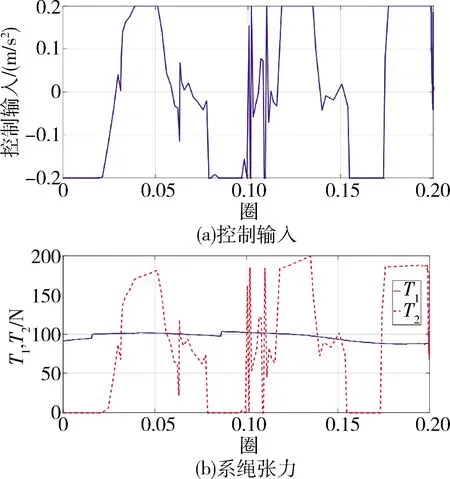
图8 控制输入与系绳张力

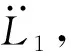
综上所述，在自稳定修正律和比例SHMPC的作用下，可以实现对非锚定PSE的轨道保持，同时，也可以对系统摆动进行抑制。通过调节控制输入，在运输任务周期结束时，系统状态参数将收敛到一个新的动态平衡状态，而相应的，需要对下端飞船沿系绳向更低的轨道进行一定的释放。

4 结论

本文基于六自由度动力学模型，对非锚定空间系留电梯的平衡状态进行了分析。研究发现，为了保证对主航天轨道进行保持并使系统达到平衡状态，可以沿系绳对下端飞船进行一定的释放。受这一发现的启发，本文提出了一种自稳定修正律，通过直接给定T1的修正律，实现对主航天器的轨道半径保持。在此基础上，面向保持轨道半径和抑制摆动的需求，提出了一种新颖的控制策略。在此基础上，考虑空间系留电梯货物运输任务特性，设计了基于比例SHMPC的控制律。仿真校验结果表明，所提出的控制策略能够在不使用推力的情况下，有效地实现主航天器的轨道半径保持，并对系统摆动进行有效抑制。