液体火箭发动机自适应克里金可靠性分析*
2022-07-27胡伟飞鄢继铨施钦杨方健豪刘振宇谭建荣
胡伟飞 鄢继铨 施钦杨 方健豪 刘振宇 谭建荣
1. 浙江大学 流体动力与机电系统国家重点实验室,杭州 310027;2. 浙江大学 机械工程学院,杭州 310027
0 引言
近年来,随着载人航天、探月工程等重大科技专项的实施,我国运载火箭进入了高强度发射期,对运载火箭高可靠、高质量等方面提出了更高的要求。液体火箭发动机是运载火箭等航天飞行器的心脏,需要具备更高的可靠度,因此对其运行过程进行故障监测,从而在一定程度上提高运载火箭的可靠性。液体火箭发动机是一类高度复杂的动力系统,由大量、相互之间存在广泛联系同时又进行着不同工作过程的组件和部件构成。随着运载火箭的有效载荷不断增加,且外界工作环境存在不确定性,使发动机工作在较为复杂的恶劣环境中。因此对其可靠性提出了更高的要求,液体火箭发动机可靠性研究受到广泛重视[1-3]。
传统可靠性分析的方法有:近似解析法、数值模拟法以及代理模型法,均适用于液体火箭发动机可靠性分析。近似解析法主要指的是一阶可靠度法(FORM)[4]、二阶可靠度法(SORM)[5],其通过将设计点的失效域边界线性化得到失效概率的估计。该类方法的缺点有:需要显性液体火箭发动机数学模型,而且在非线性问题上应用效果较差。数值模拟法主要指蒙特卡罗模拟法[6],该方法采用一定数量的样本并获取对应的响应值,基于这些样本计算失效概率。计算结果的精度随采样的样本点增加而提高。现有方法所需的计算成本和时间成本非常庞大。尤其针对液体火箭发动机这样的关键装备,获取失效样本的成本过高,收集大量数据不切实际。
基于上述结论,有学者提出了代理模型法,其主要原理为采用代理模型代替真实物理模型,运用蒙特卡罗模拟计算失效概率。蒙特卡洛法需要较为庞大的样本量,针对此,代理模型法提出将对应样本点输入代理模型当中,以较少的样本数量进行实时预测输出,减少真实物理模型或耗时的有限元仿真模型的运算次数与计算时间。现有的代理模型主要包括:多项式响应面模型[7]、神经网络模型[8]、支持向量机[9]以及克里金模型[10]。本文采用的代理模型为克里金模型,其优势在于其可以进行全局代理,获取了定义域内样本点区间的预测值,还包含预测局部方差,用于表征局部不确定性。
克里金模型对于模型的预测精确程度将直接影响分析结果的准确性,因此基于较少的样本构建精确的克里金模型是当前该领域的主要研究方向。Echard等[11]首先提出重要性采样的思想,引入重要性密度分布函数提高采样效率。在此基础上,Xiao等[12]提出了分层重要性采样的方法,进一步提高采样效率。此外Zhang等[13]提出的自适应克里金面向重要度采样方法和Wang等[14]提出的基于错误率的自适应克里金可靠性分析方法,为有效提高采样效率,拟合精确的失效边界提供新思路。但通过分析发现,现有方法大多存在样本点聚集现象, 即同一区域内样本点数量过于密集,这将导致计算资源的浪费。同时,现有方法的收敛条件不精准,容易导致过采样。
本文采用代理模型对液体火箭发动机进行可靠性分析。针对现有克里金代理模型存在的两个弊端,提出了基于泰森多边形区域划分自适应克里金的液体火箭发动机可靠性分析方法。该方法能够高效的构建克里金代理模型,并用于预测液体火箭发动机的失效概率。
1 基于代理模型的液体火箭发动机可靠性分析
1.1 液体火箭发动机可靠性分析现状
液体火箭发动机自身结构极为复杂,不同组件之间的相互作用也会对运行过程产生影响,存在随机性。图1给出了F-1发动机的组成图。针对液体火箭发动机的可靠性分析,王婷婷等[1]提出威布尔分布和Bayes估计分析方法,研究液体火箭发动机寿命分布参数以及该方法的可靠度。但这种方法未考虑液体火箭发动机实际运行时复杂环境给可靠性分析带来的不确定性,无法得到实时的可靠性分析结果。
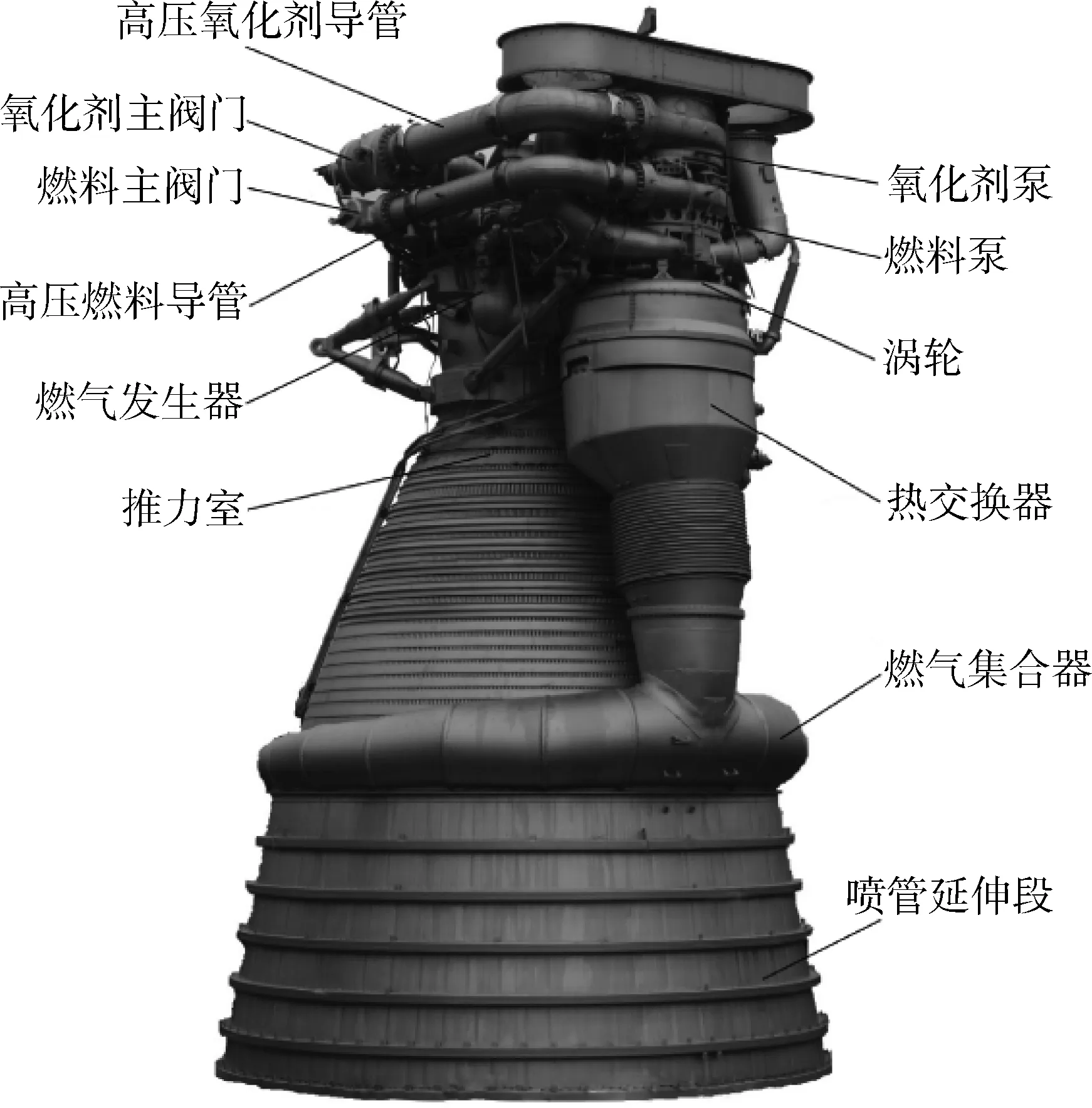
图1 F-1液体火箭发动机组成图[15]
1.2 基于代理模型的可靠性分析
本文提出采用克里金模型法对液体火箭发动机进行可靠性分析。通过建立精确的液体火箭发动机克里金模型,预测液体火箭发动机的失效概率,采用的是传统蒙特卡罗模拟方法。该方法通过采样足够数量的样本,统计处于失效域的样本数量,依照式(1)[16]计算出系统的失效概率PF。
(1)
式中,NG(x)<0定义为失效样本数量;G代表构建的克里金代理模型;NMCS为采用蒙特卡洛法采样样本点总数量。
蒙特卡罗方法计算过程中所采用的样本点越多,得到的结果越近似于真实值。在蒙特卡罗模拟计算中,得到的结果与样本点数需要满足如式(2)[16]所示的关系。
(2)
fcov(PF)为失效概率的差异系数,当失效概率的差异系数值小于0.05时,可以认为得到结果较为可信。
2 基于泰森多边形区域划分的自适应克里金模型构建方法
依据前文获得的液体火箭发动机在实际工作环境的失效概率,对其健康进行监测。计算失效概率计算失放概率的前提是构建精确的液体火箭发动机。针对传统克里金代理模型构建方法计算效率低,计算成本高等缺点,本文提出一种基于泰森多边形区域划分的自适应克里金代理模型构建方法,以较少的样本构建精确的克里金代理模型。
2.1 基于泰森多边形的全局区域划分
本文所提出的方法采用了全局区域划分策略,根据泰森多边形的区域分割方式,进行空间区域划分。具体流程如下:
根据已有样本点,生成所有相邻两个样本点的垂直平分面,进而由生成的垂直平分面将空间划分成不同的区域,此区域为泰森多边形区域。图2展示了一个由泰森多边形划分的二维案例。
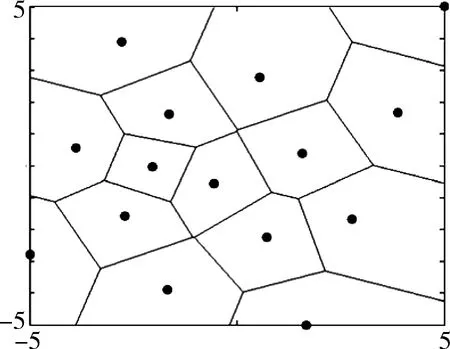
图2 一个由泰森多边形划分的二维案例[17]
由于高维样本点进行泰森多边形分割后的多边形单元是高维不规则边界的多面体,因此很难对其进行数学描述。因此,本文采用蒙特卡罗方法生成大量随机点从而近似描述高维问题中泰森多边形区域。通过计算候选样本点到空间中所有样本点的距离,将每个候选样本点划分至已有的样本点中最近的点。
2.2 改进留一法
在全局区域划分之后,需要选择出在失效边界附近的区域。该区域称为最敏感区域,采用改进留一法来实现。留一法[18](Leave-One-Out,简称LOO)是一种模型验证优化方法,常通过交叉验证检验模型的准确性。以下是留一法的具体流程:
假设空间中有N个样本,每次剔除1个样本,利用剩余的N-1个样本重新构建模型,并采用被剔除的样本作为测试集计算模型误差,进行N次流程循环,具体如式(3)所示。
(3)

将上述流程循环N次,最终得到所有样本点的预测误差。定义预测误差最大的样本点所属的泰森多边形区域为最敏感区域。
以上是传统留一法的过程。由于传统留一法是将剩下的一个点作为测试集,通过比较在这个点的响应值的偏差来比较泰森多边形区域的好坏,整个流程计算时间较长,计算成本较高。对于可靠性分析而言,只需要在失效边界附近构建精确,能够较好的拟合出极限状态函数等于0(G(x)= 0)对应的曲面即可。因此不必构建一个全局精确的克里金模型,减少不必要的计算量和成本消耗。在失效边界以外的区域,它的响应值不一定精确,只需要符号正确即可。
基于以上推论,本文所提出的方法对留一法进行修改,使其更适用于可靠性分析领域,具体流程如下:
假设空间中有N个样本,每次剔除1个样本,利用剩余的N-1个样本构建克里金模型Gi。根据构建的克里金模型Gi计算剔除后的失效概率Pfi,共循环N次。除此之外采用N个样本构建一个克里金模型,计算实际失效概率Pf。按照如式(3),计算针对每个模型的失效概率偏差,最后将偏差最大模型对应的泰森多边形区域选为最敏感区域。
2.3 主动学习函数
在计算得到最敏感泰森多边形区域之后,需在这个最敏感区域当中选取下一个样本点添加进训练集,重新构建克里金模型。本文采用的选择样本点方法为主动学习函数。主动学习函数用于确定构建模型的下一个最佳采样点,对于自适应克里金模型应用于可靠性分析领域必不可少。本文所采用的主动学习函数是预期可行性函数(Expected Feasibility Function,EFF)。
预期可行性函数fEF是由预期改进函数(Expected Improvement Function,EIF)改进而来的,由Jones等[19]在高效全局优化方法中首次提出。该预期改进函数是用来选择一个新训练样本点的位置。但是预期改进函数更多应用于构建全局精确的模型。因此本文引入了预期可行性函数,以表示预期响应的真实值满足等式约束G(x)=a的程度。其具体计算如式(4)[20]所示。
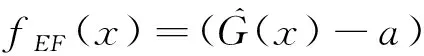
(4)

从敏感区域样本点中选取预期可行性函数值最大的点作为下一个训练样本点。通过添加新的训练样本点,建立新的克里金代理模型,采用该模型计算另一组预期可行性函,进而由该预期可行性函数选择另一个新的训练点。以此类推,直到最大点的预期可行性函数值低于指定的公差。
失效概率估计的准确性总是随着预期可行性函数停止准则的阈值的降低而增加的,但是代价是所需样本点更多,增加了计算成本。本文采用最大的预期可行性函数值小于0.001作为迭代更新的收敛判据。
2.4 整体流程
基于前文提及的方法,本文提出了一种基于泰森多边形区域划分自适应克里金的液体火箭发动机可靠性分析方法。该方法主要含有3个过程,包括全局泰森多边形区域划分,最敏感区域选择和最有价值样本点选择。其具体流程如图3所示。
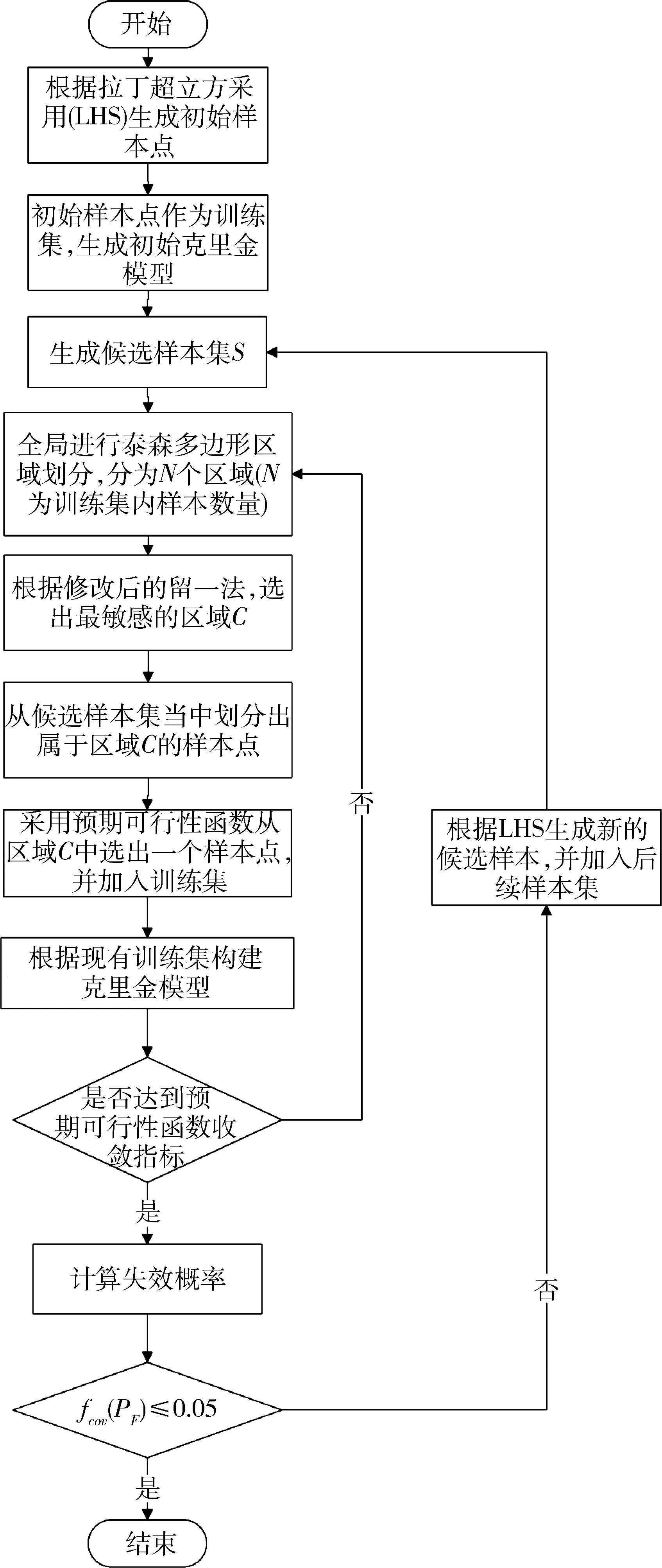
图3 基于泰森多边形区域划分自适应克里金的液体火箭发动机可靠性分析方法流程图
步骤1:根据不同输入变量分布生成少量的初始样本点X0,其中是采用拉丁超立方采样(Latin Hypercube Sampling,LHS)方法生成初始样本点;
步骤2:将初始样本点X0及其对应的输出值作为训练集X,生成初始液体火箭发动机克里金模型。具体包括:根据训练集样本X,输入到实际系统或有限元仿真模型中获得其对应的输出Y;然后根据案例类型,设置克里金模型核函数类型,设置初始参数,设置参数优化范围;将训练集输入,采用MATLAB的DACE工具箱构建克里金模型;
步骤3:根据不同输入变量分布生成一定数量候选样本集S,生成候选样本点使用的是拉丁超立方采样方法;
步骤4:在全局内进行区域划分,分为N个区域(N为现有训练集内样本数量)。全局区域划分时采用泰森多边形划分策略,使得每个多边形空间内仅包含一个样本点,且多边形内的任意位置离该多边形的样本点距离最近;
步骤5:根据改进留一法,计算失效概率偏差,选出最敏感的区域C;
步骤6:从候选样本集当中划分出属于区域C内的样本点;
步骤7:采用主动学习函数从区域C中选出一个样本点,并加入训练集X,主动学习函数采用的是预期可行性函数;
步骤8:根据现有训练集重新生成液体火箭发动机克里金模型,具体细节如步骤2;
步骤9:判断是否达到主动学习函数收敛指标,若未满足则重复步骤4至步骤8。收敛指标指的是式(5),当最敏感区域内所有样本点都满足条件时认为收敛。
max(fEF(x))≤0.001
(5)
步骤10:计算当前克里金模型下的失效概率,计算方法采用的是蒙特卡罗模拟法;
步骤11:根据式(2)判断是否满足蒙特卡罗法收敛指标失效概率协方差是否小于0.05,若未满足,则根据生成新的候选样本加入候选样本集S,并返回步骤3;
步骤12:基于现有液体火箭发动机克里金模型,根据蒙特卡罗模拟法计算系统失效概率Pf。
3 案例分析
本章采用的测试案例是基于杨晋朝[21]提供的液体火箭发动机失效数据,得到的液体火箭发动机性能方程,如式(6)所示:
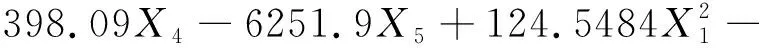
(6)
式中,5个输入变量分别是氧泵入口压力X1、氧泵后温度X2、氢泵入口压力X3、氢泵后温度X4以及燃气发生器室压X5均服从正态分布,均值0.5,方差0.1,5个变量相互独立。
在测试过程中,初始样本点选择为12个,每次生成的候选样本集数量为105个。将本文所提出的方法与传统的自适应克里金模型-蒙特卡罗模拟方法[20](An active learning reliability method combining Kriging and Monte Carlo Simulation, AK-MCS)作比较,并采用蒙特卡罗模拟结果作为真实值。并通过5次仿真测试后求取平均结果,验证本方法的鲁棒性。最终的实验对比结果如表1所示。表中展示了两种方法所需的样本点个数和误差率。从表中可以看出,本文所提出方法与传统自适应采样方法的计算误差都小于1%,达到精度计算要求。此外,本文提出方法所需的样本点个数仅为163.4个,而AK-MCS方法需要314.2个样本点。在本案例中,本文所提出方法效率比AK-MCS方法提高了48%,相对于传统方法能够快速、准确地对液体火箭发动机进行可靠性分析。

表1 测试案例结果对比
4 结论
针对传统可靠性分析方法计算效率低的问题,本文提出了一种基于泰森多边形区域划分自适应克里金的液体火箭发动机可靠性分析方法。利用泰森多边形进行全局区域划分,结合改进留一法对区域进行筛选,极大程度的提高了模型构建的效率,能够用较少的样本点构建同样精度要求的液体火箭发动机模型。同时,该模型能够结合外界载荷的不确定性,对发动机进行健康监测和故障检测。在理论测试中,基于本文提出方法构建的代理模型测试计算误差与其他模型相比小于1%,效率提高了48%。本文侧重于理论方法研究,如有真实液体火箭发动机模型或有限元仿真模型,采用本方法也能对其进行可靠性分析,计算出特定工作状况下的失效概率。
后续工作可以从液体火箭发动机时变可靠性分析研究着手,将外界载荷的时变特性纳入考量,研究一种高效的时变可靠性分析方法。
