基于田口算法的机电液耦合器结构优化

吴玉杰

（郑州机电工程研究所，河南郑州 450000）

目前内置式永磁同步电机是现阶段汽车现代化发展的重要发动机，但这种电机有一个较为突出的缺陷，即借助机电能量媒介转换[1]。为此，在进行电机设计期间和使用期间，必然存在电流过载而引发的发热、退磁等问题[2]。机电液动力耦合是电动车进行动力传动的重要组成环节，借助控制器能够保证车辆实现高效运行[3]。要实现对电机运行质量、效率的调整，就必须结合机电液动力耦合器电磁的特征，对其结构参数做出优化处理，通过控制柱塞对磁路的影响，实现机电液动力耦合器电磁性能的提升，从而改善电机问题。

1 机电液耦合器电磁结构有限元仿真

采用Maxwell 电磁场有限元分析进行机电液耦合器电磁结构的仿真处理。在对电机进行设计期间，电感与磁链作为能够体现电机性能参数的主要指标，其不仅受电磁耦合、结构尺寸以及非线性材料的影响，同时伴随着电机运行空间、时间等方面的改变，电感的变化能够更为准确地判断电机的复杂磁场状态。根据仿真模型，磁力线经由N 极出发在到达S 极后即可形成闭合回路，气隙以及磁桥部位漏磁情况相对有限[4]。同时，在受到柱塞腔的影响下，导致q轴磁路狭窄，磁阻迅速增大，故而导致电机磁阻转矩较小，严重影响弱磁性能。

2 确定优化目标和优化变量

结合仿真模型分析结果，确定机电液耦合器电磁结构的结构优化，关键就是解决q轴磁路的结构参数增大凸极率，从而实现对输出电磁转矩的提升。

在机电液耦合器进行大转矩运作时，可触发柱塞泵工作，经由斜盘旋转引发转子内柱塞轴进行往复运动，将液压能转变机械能，柱塞泵在实际运行期间，转矩会产生不可避免的脉动变化。机电液耦合器电驱系统在工作期间，必然会带动转矩脉动，但若脉动过大可能会使其整体运行稳定性发生改变。为此，在对磁路结构优化处理期间，在保障输出矩阵增加的同时，还必须确保机电液耦合器的脉动控制到最低。

转矩脉动主要包括了两个部分：即纹波转矩、齿槽转矩。其中纹波转矩的计算公式如下：

式中，Th为纹波转矩；Tmin矩阵脉动最小值；Tmax转矩脉动最大值；Tavg平均转矩示；Bs定子磁密；m 谐波的次数；Br转子所能够提供磁密度。

根据公式（2）可知，纹波矩阵实际上是定转子各次磁密谐波相互作用的结果，当定转子磁密谐波达到相同状态，且达到了6 m±1时随后会产生纹波矩阵，并且纹波矩阵的大小与定转子磁密谐波的次数之间呈现正相关性。即纹波次数越多，纹波矩阵就必然会越来越大，合理的转子永磁体布置方式能够较好地控制纹波矩阵。

永磁体在进行布置期间，不同的形式会对纹波矩阵带来不同的影响，同时还会对齿槽转矩带来相应影响。极弧系数与齿槽转矩之间的关系见式（3）：

据式（3）中，La电机轴向的有效长度；Ns主要用于对定子槽数进行表示；Bσ气隙磁密幅值；NL定子槽数最小公倍数以及永磁体极数；R1与R2电机气隙的内径与外径；ap则表示极弧系数；Kskn表示斜槽因素；as为斜槽/斜极角度；a 为永磁体相对齿槽之间的距离。

结合式（3）来看，通过对极弧系数进行调整，可实现对永磁体布置的调整，从而减少耦合器转矩时的波动反应。选取丰田prius 的“V”型转子结构可了解到永磁体励磁角度在达到133.5°时，即可取得最小谐波反应。

文章选取极间间隔a（mm）、磁钢厚度b（mm）、磁肋底到轴的距离c（mm）和磁钢宽度d（mm）作为设计变量，根据图1，永磁体励磁角度实际上受到c、a的影响，而d与角度又可对气隙磁的波形以及大小带来直接影响。为此，a、b、d、c均是参数优化重点。

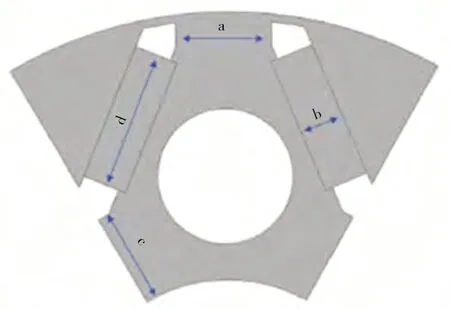
图1 优化参数

定义单位面积永磁体APM 产生转矩Tm 表征机电液耦合器对永磁体利用率的计算公式：

式中，Tm单位面积永磁体产生矩阵，Tavg平均转矩，Tcog是指齿槽转矩阵的最大值，Th是指纹波转矩，这是作为机电液耦合器最优的目标，确保其能够在达到最大矩阵时控制永磁体的实际用量，并将转矩波动控制到最低。最终，获得优化参数与目标的关系公式：

3 正交试验

基于AnsoftRMxprt 软件对上述优化目标参数的性能曲线进行试算，结合性能曲线即可获得最优化参数取值结果，见表1。基于不同优化取值范围，选取3个从小到大的水平值。

表1 优化变量水平值 单位：mm

在本次试验中，共获取了4个不同的优化变量，各个变量选取3个相应的水平值。基于田口算法下进行正交试验矩阵，构建起三水平L9（34）正交矩阵来保障各列获得相等次数的试验，同时还能减少不必要的试验次数，提升整体优化效率。注重完成了9次正交试验，试验结果见表2。

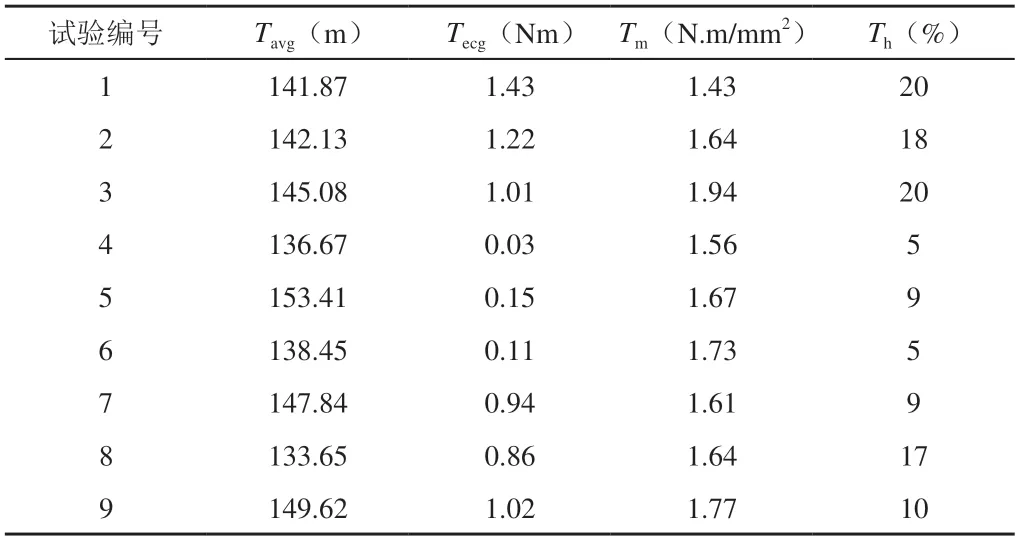
表2 正交试验值

试验1所对应的是初始参数，为了进一步了解优化变量的影响效果，对其进行平均值分析和方差分析，并计算各参数的影响比重，见表3。

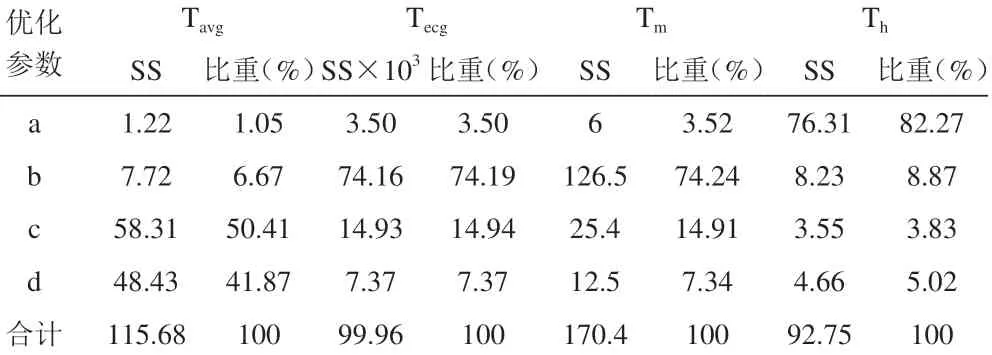
表3 各优化变量对电机性能的影响

从表3来看，不同参数的影响程度各不相同，基于不同比重结果，最终确定最优参数值：a为10 mm，b为4.8 mm，c为16 mm，d为17.5 mm。

4 优化结果对比分析

为验证该参数是否能够实现对机电液耦合器电磁性能的优化，通过有限元仿真软件进行验证，观察转矩特性曲线发现（图2），机电液耦合器电磁性能得到了非常显著的提升，输出转矩尤其明显，同时转矩的波动明显较小。基于此，对比原有模型，其性能结果显示，优化后机电液耦合器电磁的输出转矩、磁钢利用率等指标均有明显调节（见表4）。

表4 优化前后性能对比

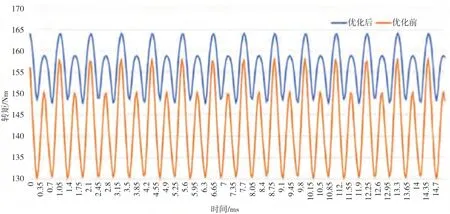
图2 输出转矩对比

5 结论

本研究结合机电液耦合器电磁结构优化的研究课题，提出了运用田口算法的优化模型，得出以下几点结论：

（1）机电液耦合器电磁性能优化要点，解决q轴磁路的结构参数增大凸极率。

（2）田口算法确定，对极弧系数进行调整，可实现对永磁体布置的调整，从而减少耦合器转矩时的波动反应。

（3）正交试验最终确定最优参数值：a为10 mm；b为4.8 mm；c为16 mm；d为17.5 mm。

（4）优化参数可调节输出转矩、磁钢利用率等指标。