激光散斑的漂移现象以及数值模拟方法
2022-07-26李可妤郭嘉钰
徐 蕾,李可妤,郭嘉钰,钟 鸣
(南京师范大学 物理科学与技术学院物理系,江苏 南京 210000)
散斑现象普遍存在于光学成像过程中,其携带了光束和光束所通过的物体的许多信息,因此被广泛应用于光学领域[1-3].
当一束激光打到粗糙表面上时,反射光会干涉成像,形成明暗不同的斑点,这样的图案便是散斑.而即使保持所有的仪器静止,我们依旧会发现,散斑在“漂移”.对于这一现象的研究有利于进一步认识散斑,从而提高散斑成像的精度,具有现实意义.
经过我们的分析,激光束照射的位置总体不会发生改变,而散斑之所以看起来在漂移,实质上是反射光干涉后的光强分布发生了动态变化,在视觉上就表现为“漂移”,类似于显示屏通过交替点亮LED产生滚动字幕的效果.为了进一步研究这种现象,本文将通过多项实验来寻找散斑漂移的主要因素,并且会根据这些因素进行仿真模拟来重现散斑的动态变化.
1 分析方法与实验内容
1.1 分析方法
我们通过相机拍摄记录下散斑从产生到漂移稳定的过程,将其导入软件中进行分析.分析过程涉及以下两个概念.
相关系数γ可以有效比较两幅散斑图像间的相关性,其表达式为[4,5]
(1)
其中,pj=Ij(xi,yi)-〈Ij(xi,yi)〉,I1(xi,yi)为t=0时刻的散斑图案位于(x,y)坐标上的光强,I2(xi,yi)为t>0时刻的散斑图案位于坐标(x,y)上的光强.
为了比较不同时刻一个散斑漂移的快慢,我们定义了相关系数的变化率,其表达式为
(2)
为了减小时间间隔带来的影响,我们将每20个时间间隔,取一次变化率的平均值,v的平均值越大,表示散斑变化得越快,即“漂移”得越快.而当v的标准差趋于0时,说明变化率维持稳定,即散斑的“漂移”维持稳定.
1.2 实验装置
实验装置如图1所示.摄像机帧率为30 fps,选取波长为635 nm的红色激光笔,粗糙表面为卡纸与磨砂纸(较薄).另外,使用焦距为10 cm的凸透镜以放大光路,方便拍摄.摄像机、激光笔、凸透镜、粗糙表面四者皆固定于光具座上,调节至一条直线.在黑暗的实验条件下进行拍摄,确保激光笔是唯一的光源.我们在实验中调节各仪器间的距离,使得在表面上成像的散斑大小直径为6 mm左右.

图1 实验装置示意图
1.3 实验内容与数据分析
激光具有能量,由于激光加热而产生的一系列热效应很可能会造成干涉结果的变化,使肉眼看到“漂移”的现象.以下设想了2种可能:空气受热膨胀,导致折射率变化;粗糙表面受热膨胀.两者在不同程度上都将造成光程差的变化.下面将通过实验来验证上述猜想.
1.3.1 散斑漂移的特征
对一个散斑进行600 s的拍摄,在500 s处使用小风扇在远离表面处吹风,使得激光经过的空气产生流动,而表面不受到这一流动的干扰,其相关系数以及相关系数的变化率随时间的变化关系如图2所示.图2(a)描述的是相关系数随时间的变化,黑点是实验中实际采集到的数据,黑线则是对数据进行平滑处理后得到的连续曲线(后面的分析如果没有特殊声明,其实验结果都经过了平滑处理).图2(b)描述的是漂移速率以及漂移的稳定性(漂移速率的标准差)随时间的变化.
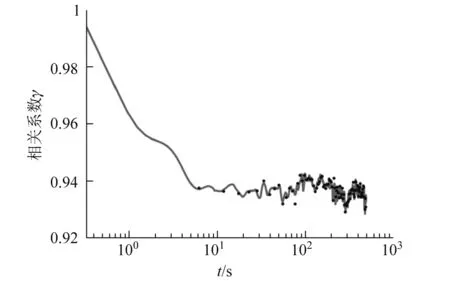
相关系数随时间的变化
从图2(a)不难发现,在最初的10 s内,散斑的相关系数不断下降(至0.93左右),而后开始呈现上下震荡,震荡幅度逐渐减小.600 s后,相关系数仍保持一定微小的震荡.图2(b)显示漂移速率与漂移的稳定性先下降(大约持续10 s)后震荡,随着时间推移,漂移速率维持在一个较为稳定的值(0.002 7左右),漂移速率的标准差基本为0,也就是说散斑的漂移由快至慢,由不稳定至稳定,最终散斑处于动态平衡.实际上,在大约180 s后,肉眼很难再观察到散斑的漂移,但通过软件分析,散斑依旧处于漂移状态.
值得注意的是,当我们在500 s时给空气一个扰动后,接下来的100 s内,散斑并没有出现剧烈的变化.从而认为空气的热效应并非是散斑漂移的主要因素.我们在同样的实验条件下,重复上述实验,其相关系数的变化,漂移速率的变化在宏观上是一致的(主要表现为变化的趋势,达到相对稳定所需的大致时间,达到相对稳定时的相关系数以及漂移速率的大小等),下面重点关注的便是散斑漂移时的宏观性质.
1.3.2 研究粗糙表面的颜色的影响
我们分别选取了同一款品牌的黑色和红色卡纸作为粗糙表面进行实验.实验结果如图3所示.
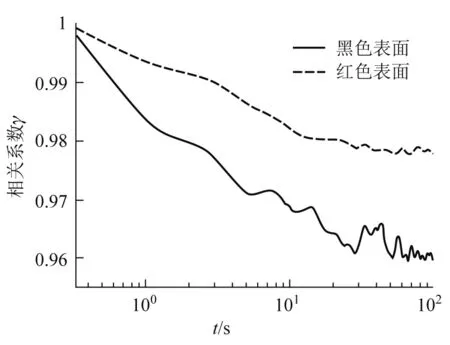
图3 不同颜色粗糙表面产生的散斑相关系数随时间的变化
图3显示黑色卡纸产生的散斑漂移得更快,达到稳定需要的时间也更长.这是因为对于相同功率的激光,黑色卡纸相较于红色卡纸而言,对光的吸收率明显更大,因此黑色卡纸接收到的能量更多,表面膨胀更快,光线的相位差变化更快,最终造成干涉的结果——明暗变化更快[6,7].同时,由于黑色卡纸吸收更多热量,黑色卡纸最后温度变化更大,其形变程度更大,导致散斑基本稳定的时候,相关系数变化更大.而黑色卡纸吸热膨胀的过程持续更久,因此散斑达到稳定需要的时间也更长.
这就使得我们确认了导致散斑变化的一个主要因素——粗糙表面的热效应.
1.3.3 研究表面粗糙程度的影响
选择粗糙程度不同,材质相同的磨砂纸进行实验.以cw(国产砂纸的粒度,粒度是指颗粒的大小)来描述粗糙程度的大小.
图4描述了不同粗糙程度磨砂纸产生的散斑的相关系数随时间的变化关系.显而易见的,这些相关系数的变化没有很大差别.回顾实验条件,被选取的表面磨砂纸与卡纸较为薄大,而激光只照射到非常小的一块区域,表面切向膨胀不易,因此法向膨胀占据了主导地位.由于散斑是无数光波的叠加,理论上通过大量统计后,不论粗糙程度的大小如何,其最终造成的干涉条件的变化是等效的.这样就能很好解释我们图4中呈现的实验结果.由此可见,在我们的实验条件下,粗糙程度只是漂移的一个次要因素.
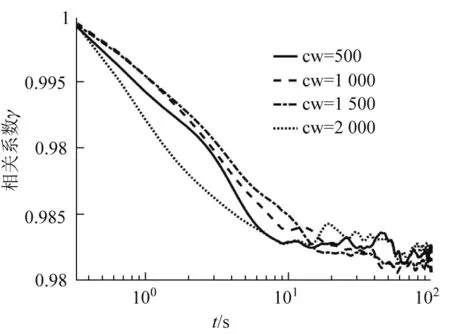
图4 不同粗糙程度下散斑相关系数随时间的变化关系
1.3.4 激光笔功率的影响
使用两片偏振片来改变激光笔的功率.偏振片平面与激光光束垂直,θ为两片偏振片的夹角,当θ=0时,激光笔的功率是最大的.结果如图5所示.
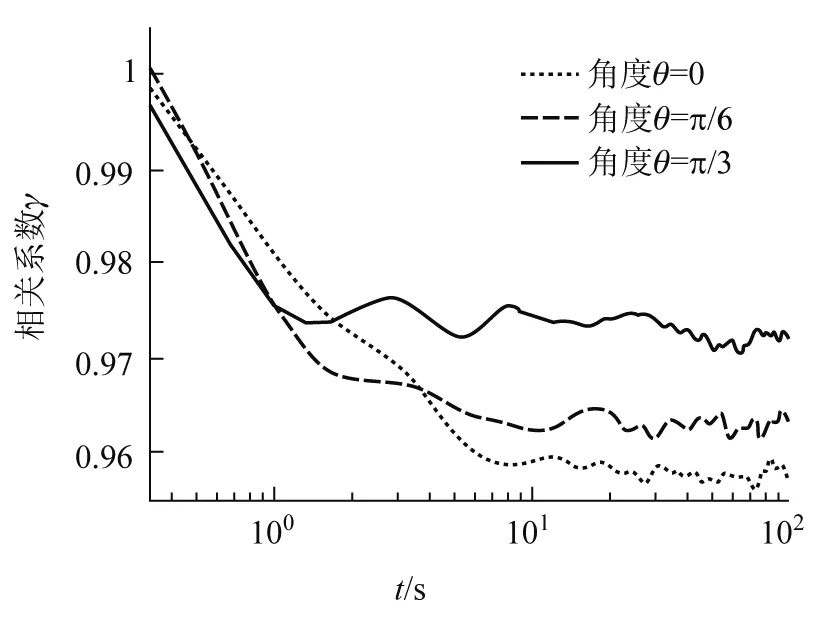
图5 不同激光笔功率产生的散斑相关系数随时间的变化
从图5中明显可见功率大的激光产生的散斑漂移更快,需要更长时间达到稳定.这样的结果不难理解,功率大的激光能让粗糙表面更快发生形变,这里就不做过多赘述.
值得一提的是,在经过上述实验条件的变换后,散斑漂移的特征基本不变,都是由快至慢,由不稳定至稳定.因此实验1.3.1中对散斑漂移特征的描述具有普适性.
2 数值模拟
经过上面一系列实验,我们得出散斑漂移的主要原因为:激光加热→表面受热膨胀→相位改变→干涉结果改变(明暗变化)→宏观“漂移”.
为了再现这一现象,下面将通过数值计算来模拟这个动态过程.
2.1 散斑的形成
散斑是无规则散射体的相互叠加.为了模拟一个散斑,首先需要随机生成一个粗糙表面矩阵s(即随机生成数的矩阵).
其次,通过式(3)、式(4)得到散斑振幅大小.其中o(x0,y0)是由于粗糙表面反射造成的相位差,由式(5)表示.像平面任意一个点A(x,y)的振幅是激光束经过表面发射后振幅A0(x0,y0)不同比重的叠加,这一比重通过h(x,y)描述,h(x,y)的形式由式(6)表示.
A(x,y)=∬A0(x0,y0)h(x0,y0,x,y)dx0dy0
(3)
A0(x0,y0)=E0(x0,y0)exp(o(x0,y0)i)
(4)
(5)
(6)
其中,a为有效光斑的半径大小.z为像屏与光斑的距离,λ为激光束的波长.而E(x,y)为激光的复振幅,我们将激光看成高斯光束,那么,E(x,y)的振幅呈高斯分布.J1为一阶贝塞尔函数[8-10]最终,模拟散斑的相对光强为振幅的模.
在对实验中拍摄的视频进行图像处理时,灰度值即为光强,而设备对灰度值的存储范围有限(0~255),因此我们在模拟散斑时,对散斑光强大小进行了上限处理,当光强大于x(某一值)时,光强取为x.
生成散斑后,我们将模拟的散斑与实验中的散斑进行光强的对比,结果如图6所示.

实验中拍摄到的散斑
实验与模拟的散斑存在着一些差别.主要来源于以下几点:在实验中,表面有7~9本底灰度值,这是无法避免的.而在数值模拟中,表面的本底灰度值为0.在拍摄过程中,由于摄像机分辨率原因,采集到的散斑相对于模拟的散斑模糊.但模拟总体上已经再现了散斑.
2.2 散斑的动态变化
由于激光束照射表面,导致表面的温度变化.在这一步中,考虑模型理想化的几个点:1) 只考虑激光对表面的加热,表面厚度非常小,膨胀时,以法向膨胀为主;2) 表面的吸光率是恒定的;3) 激光功率是恒定的;4) 光斑边缘的温度是恒定的室温.
列出热导公式
(7)
其中,k为热导率,C为表面的比热容,ρ为表面的密度,q为激光对表面的加热功率,有
(8)
r为传播轴线相交于z的的高斯光束等相面上的光斑半径,α为表面的吸光率,ω为高斯光束等相面上的光斑半径,E0为光心处的振幅.
由于热膨胀导致的相位改变为
(9)
β为表面的线性热膨胀系数,d为表面的厚度.这样的相位变化最终导致散斑形成过程中式(5)的变化.将式(5)与式(9)叠加,便形成新的表面.合成新的散斑.
得到表面随时间的变化后,用不同时刻的表面生成散斑,计算这些散斑的相关系数,实现对漂移这一动态的模拟.由于相关参数的精确测量是难以实现的,因此本次模拟参数有着如下所述的参考范围(仅适合本文中所描述的实验情况):表面的热导率约为0.07~0.12 W/(m·K),表面的比热容约为1.7×103~2.1×103J/(kg·K),表面的密度约为0.85×103~0.9×103kg/m3,激光笔的最大功率约为0.95~1.0 W,表面的吸光率约为0.8~0.85,表面的线性热膨胀系数约为8×10-6~9×10-6K-1,室温为283.1 K,激光直径为6 mm,表面厚度为0.08 mm,激光波长为635 nm.通过不断调整模拟的参数,虽然无法完全再现真实的散斑漂移,但是能在趋势以及数量级上尽可能贴近实验.图7呈现了模拟结果与实验的对比.

图7 模拟与实验中产生的散斑相关系数随时间的变化关系
模拟与实验得到的结果有一定的吻合度.不同的是,当模拟足够时长时,表面会到达热平衡,此时,散斑的相关系数不再会改变.但是实际实验中,空气的流动、浮尘、激光光强的衰减、表面的径向膨胀等众多因素,都将导致散斑无法达到绝对的平衡.因此,相关系数会震荡.
3 总结
肉眼观察到的散斑漂移现象的本质是散斑定点光强的明暗变化,宏观表现为漂移.我们通过实验发现,造成散斑漂移的最主要因素是激光的能量导致了粗糙表面的膨胀,而表面升温过程升高由快至慢,因此其相关系数的变化率(漂移速率)也是由快至慢,而后期,肉眼几乎看不到散斑的变化,散斑达到一个相对稳定.
考虑到表面膨胀为散斑漂移的主要因素,我们构建了完善的模型,得到散斑动态变化的数值模拟.虽然这一模型忽略了很多次要因素,但是模拟下来的结果与实验较为贴合.可以对此借鉴,进行进一步研究.
