散射介质成像中光学记忆效应概念及其进展

王玉杰，周 昕，白 星，杨忠卓，余 展，陈星宇

(四川大学 电子信息学院，四川 成都 610065)

人们从外界获取信息的主要方式是通过眼睛直接观察或借助物理装备辅助人眼成像.这种传统的成像方式是在无散射介质的情况下，通过记录弹道光子，然后在空间上分布再现弹道光子所携带的物体信息来实现的.但是在实际生活中，普遍存在的散射介质会不同程度地影响传统光学成像方式的效果[1].例如，天文观测上，地面站台由于受空气中散射颗粒的扰动，只能看到闪烁的星星和模糊的光影；卫星遥感光学成像受大气和云层的影响，图像利用率很低；在雾霾、雨雪等恶劣天气条件下，会影响驾驶员观察而导致事故多发；在临床医学诊断中，观察目标周围的各种生物组织对成像效果造成干扰等等.可见，如何克服散射介质的影响，利用散射光成像实现对介质后方待观察物体进行高质且快速的成像，是长期以来光学成像技术领域期望解决的重大问题.

在科研人员长期不懈的努力下，散射介质成像技术已取得了很大的进步.尤其是近几十年来，随着新技术、新工艺的发展，诸如空间光调制器(SLM)、数字微镜器件(DMD)、微机电系统调制器(MESM)等数字波前整形器件相继出现并应用于散射成像研究中，出现了多种具有一定实用性的散射介质成像方法，如光学相位共轭、波前反馈调节、飞行时间法、自适应光学技术、波前整形、光学传输矩阵等，极大地促进了散射介质成像技术的实际应用.与此同时，光学记忆效应概念的提出，为散射介质成像研究打开了新的局面.最具代表性的就是2012年荷兰特温特大学的科学家Bertolotti等人[2]基于光学记忆效应提出了散斑自相关方法，并成功地运用在散射介质成像中，揭开了利用光学记忆效应实现透过散射介质成像的序幕.基于光学记忆效应的散射成像技术，具有非侵入的特点，并且对光源和系统的要求较低，可以仅采用非相干光照明，而不是昂贵的激光器、光场调控器件和复杂的机械扫描或控制等系统，因而展现出强大的应用潜力.2014年，瑞士科学家Yang等人用自相关方法实现了生物组织后方红细胞的成像；2015年Bertolotti团队的Yilmaz等人在该方法的基础上引进高折射率散射介质作为成像透镜，成功实现了对直径100 nm的荧光小球的成像.不过这两种方法还是采用的相干光作为光源物体，且光源必须保持静止.2014年，Katz等人[3]利用空间非相干光源照明物体，首次实现了一种单次曝光的非侵入式的成像方法，利用解自相关方法完成了单次非侵入式成像恢复.在此基础上，2016年美国的研究者Edrei等人通过提前测出系统的点扩散函数，实现了散斑解卷积成像.解卷积的成像方法与自相关方法相比，具有更高的信噪比和更快速的恢复成像时间，因此成像质量更好.同年周建英团队和Scarelli团队先后提出将解卷积技术用于透过散射体后的成像恢复，得到了实时、彩色、大视角和超分辨率的成像恢复结果.2018年新加坡Tang等人用同样的方法实现了大视场成像.2019年上海光机所提出了双屏模型，揭示了光学记忆效应本质就是高阶空间的时不变性.

可以看到，光学记忆效应概念的提出揭示了光场散斑之间微妙的关系，极大地促进了散射介质的成像技术的研究，为后来出现的散斑自相关技术和散斑解卷积方法提供了理论支持，加快了以非侵入方式实现成像技术的研究进展.因此，光学记忆效应现象的发现及概念的提出，在散射介质成像领域中具有极其重大的意义，预计在今后仍将是解决散射介质成像问题的重要途径.但是基于光学记忆效应的成像技术目前仍面临着成像范围较小、难以达到大视场效果等进入商业实用化的瓶颈障碍，因此如何扩展记忆效应的成像范围是未来该领域研究需要关注的核心问题.本文结合目前最新研究成果，对光学记忆效应概念的提出、发展以及在研究散射介质中的重要作用，进行了全面的介绍，并对其今后的拓展做了预测，提出广义光学记忆效应的概念.

1 光学记忆效应概念的提出

当一束均匀的激光照射在纸张或者墙壁上并反射时，观察者会看到对比度高而且尺度细微的颗粒图案，这种颗粒结构被称为“散斑”.当激光穿过散射体或空间中悬浮的微粒时也会有类似的散斑现象出现.散斑的产生就是因为介质的散射作用，即光在传播时受到介质微结构的作用而改变其传输方向、偏振态、甚至频率的现象，进而在空间中形成了光强随机分布的图案.20世纪80年代，Feng等人[4]在散射介质传输系数的研究中发现，当入射激光转动一个小角度时，从散射介质出射的光场也会随之转动相同的角度，但随机分布的散斑图案几乎保持不变，直到角度超过一定的临界值，散斑图案才发生根本变化.也就是说，散射光形成的散斑图案似乎存在散射介质的记忆中，他们将此现象命名为光学记忆效应.为了更加清晰的认识这种现象，之后Freund等人[5]在实验上证实了该结论，图1所示为他们的实验结果.可以看到，当入射角度轻微调整时，所得散斑与之前的散斑具有很强的相关性，但随着角度的逐渐增大，相关性逐渐减小直至消失.进一步的研究发现光学记忆效应只与散斑介质的厚度L有关，而不依赖其他参数，其范围可以用关联函数的一阶效应来表示，即

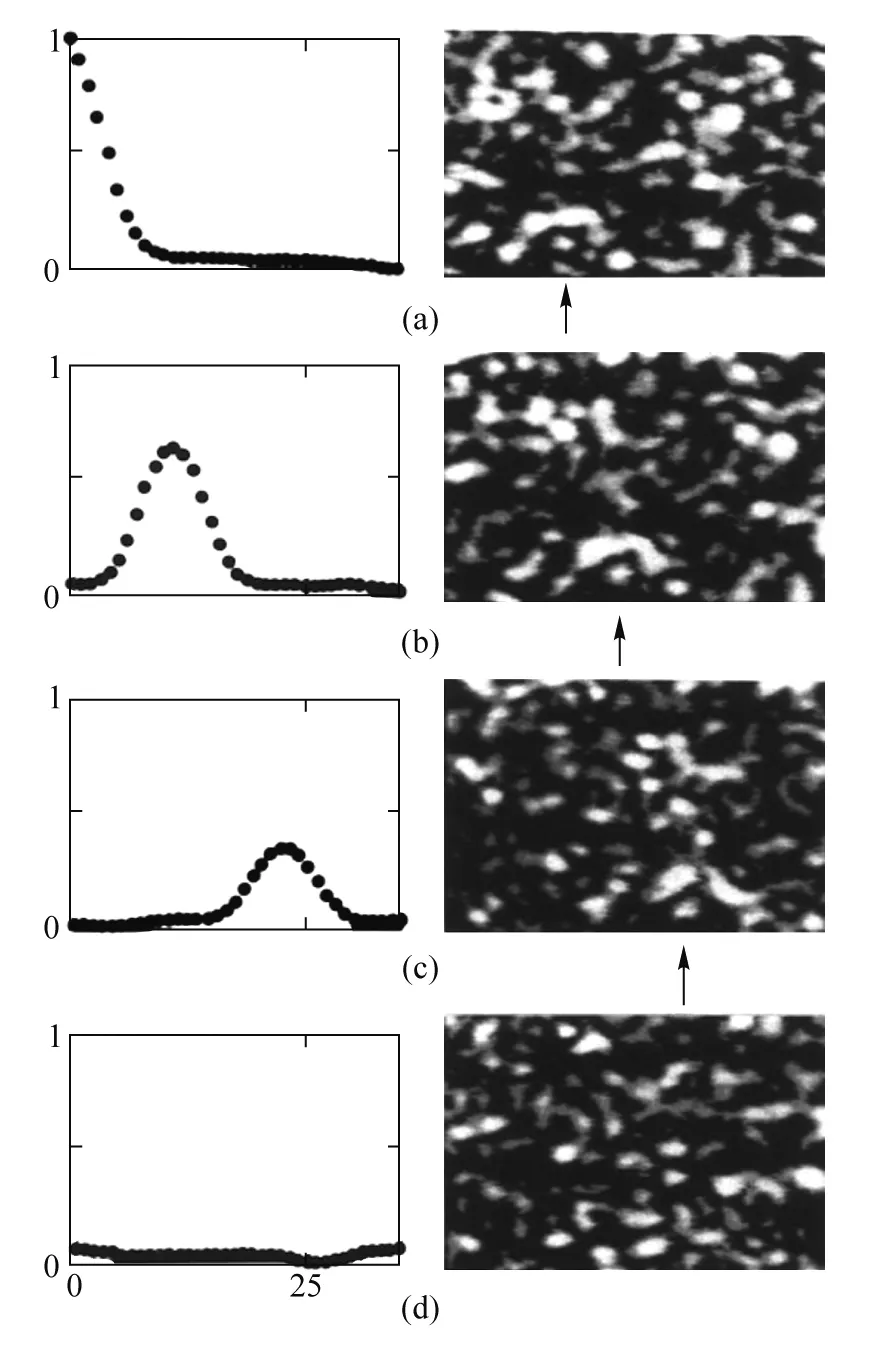
图1 光束入射角度改变下的光学记忆效应实验图

(1)

其中q=2πδθ/λ，δθ为转动角度，L代表散射介质的厚度，C代表相关度.

随后，Judkewitz[6]于2015年又提出了平移光学记忆效应的概念，是以角度表征的光学记忆效应概念的一种延伸.如图2所示的平移光学记忆效应，是指入射光束在垂直于入射方向上平移一段小的距离之后，从散射介质出射的散斑光场也跟着平移一个距离，且散斑图案基本保持不变，直到入射光束平移距离足够大时，出射散斑图案发生根本变化.不难看出，平移光学记忆效应实际上是角度光学记忆效应在光源位于无限远情况下的一种特殊情况.

图2 传统的角度记忆效应和平移记忆效应

光学记忆效应概念的提出，首次揭示了散斑之间相互依存的关系，为其后非侵入成像的方法的研究奠定了理论基础.基于该记忆效应发展的透过散射介质的成像技术主要有散斑自相关和散斑解卷积两大类别，能实现高质量快速的恢复物体，但受限于光学记忆效应的范围较小，使得难以达到大视场效果等进入商业实用化的瓶颈障碍，因此迫切的需要提高光学记忆效应的成像范围.

2 光学记忆效应概念的延伸

有学者研究发现，可以通过物理方法辅助扩大光学记忆效应的范围.例如Antip等[7]利用一种定制的超大记忆效应范围的准散射体，实现了解卷积的三维成像恢复；Liao等[8]利用检测不同轴向位置的一系列点扩散函数，通过利用不同轴向位置的光学记忆效应组合实现了沿轴方向的景深拓展；Shaoo[9]使用单色相机演示单镜头多光谱成像，利用不同光谱下的光学记忆效应的去相关操作实现了多光谱成像.图3为Shaoo等人的实验中，多光谱物体的光通过强散射介质在单色照相机上产生散斑图案，不同的波产生的散斑不同.用单色相机记录在不同光谱带照亮中心点物体时所产生的点扩散函数，然后利用各光谱对应的点扩散函数，从单色散斑图像恢复出相应波长的图像，最后将各个单光谱叠加起来得到物体的全光谱图像.

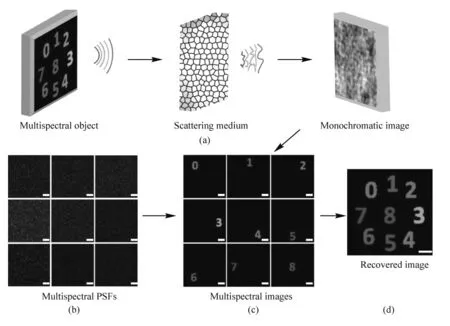
图3 光谱成像示意图.(a) 多光谱图像的传输过程；(b) 对应的散斑图样；(c) 多光谱成像；(d) 合成结果

不过，这些借助辅助手段实现光学记忆效应范围的扩大，在本质上并没有改变光学记忆效应概念的内涵.随着研究的深入，这一概念逐步向涵盖空间域和频谱域的范围延伸.

在Feng等人的研究中，光学记忆效应表现为：当光束的入射角改变一定值时，从散射介质出射光场的随机散斑图案几乎不变，而仅仅是相应跟随入射光改变一定角度.这可以理解为在相应入射角范围内，散射介质的点扩散函数保持较大的相关性；随着入射角度的不断增大，PSF相关度逐渐降低，直至完全不相关.我们可以把这种认识进一步拓展，不仅局限于考察入射光场的入射角引起的PSF相关性变化，而是拓展到不同空间距离、不同光谱波长的散射光场散斑图案的相似性，也就是考察在这些不同条件下散射介质PSF的相关度.目前已经有相关研究人员关注到这方面的问题，如Xu等[10]研究了不同光谱波长下PSF的相关度变化.在他们的实验中，利用不同光谱波长对应的散斑图案实现了多光谱记忆效应.这种基于多光谱记忆效应的表现为：只要对不同频谱的点扩散函数进行适当的空间放缩，就能使得它们之间的相关性最大化.图4为Xu等人的实验结果，在空间位置相同的情况下，用两种光谱完全不重叠的LED进行照明.如图4(a)和4(b)所示，分别为两不同波长得到的散斑图样，其中一个波长的点扩散函数是已知的.通过对已知的PSF进行适当的放缩，估计出另外一个波长的点扩散函数，进而恢复出另外一个波长物体的形状，缩放大小满足的条件为t=λ1/λ2.从该实验中可以看出，在透过散射介质成像时，由于波长变化而导致的点扩散函数变化是有很强相关性的.从侧面说明当面对某一个波长的已知物体和另一波长的未知物体时，仅通过一次拍照就可以恢复出未知物体的形状，从而在全光谱范围内实现多光谱成像.

图4 用PSF缩放法对不同波长同深度的物体进行成像.(a) 已知波长的散斑图；(b) 未知物体的散斑；(c) 进行放缩后相关得到的结果；(d) 直接相关的结果

另外，物体的轴向位置也对光学记忆效应有一定的影响.在不同平面的物点之间也存在一种特殊的相关性，只需要测得一个物平面的点扩散函数，通过缩放因子便可以推导出其它平面的点扩散函数,因此也可称其为轴向光学记忆效应.以Xie等人[11]的实验结果图5为例，在同一波长下如果不对点扩散函数放缩，会得到很差的运算结果，如图5(g)所示.如果按照q=f′/f放缩可以很轻松的得到重构物体结果，如图5(h)所示.从Xie实验的结果可以看出，通过轴向光学记忆效应能有效地扩展成像的景深.与原始方法相比，该方法提高了约为五倍景深分辨率，并且能从单幅散斑图像中恢复超过原始景深的3个物体.基于此方法可以通过先探测物体不同平面，再通过组合成完整物体从而实现立体成像.

图5 用PSF缩放法对相同波长但不同深度的物体进行成像.(a) 参考对象；(b) 一个未知的对象；(c)和(d)分别是参考对象和未知对象的散斑；(e)是从(c)检索到的PSF；(f) 是缩放的PSF；(g)和(h)分别是直接成像和放缩PSF成像

由上述可以看出无论是轴向光学记忆效应还是多光谱记忆效应，都可以用下式来概括表示为

(2)

其中PSF1和PSF2分别表示在不同的时空位置的点扩散函数，t为缩放因子.式(2)可以理解为在多光谱及轴向位置改变的情况下，只要通过尺度缩放来实现PSF的高相关度，则该时空区域均处于光学记忆效应范围.

这与光学记忆效应概念在最初提出时，即基于入射光束转动前后的高相关度，在本质上是相同的.也就是说，式(2)中是利用改变不同条件前后的PSF相关度，而在传统光学记忆效应中则是利用转动前后散斑的相关度，由于转动前后散斑的相关度实质上就取决于PSF的相关度，因此这两者在本质上是相同的.从另一方面来讲，式(2)可以理解为拓展了光学记忆效应的适用范围.

3 展望

上面将光学记忆效应概念拓展到不同轴向位置以及不同波长，极大地延伸了光学记忆效应的适用范围.如果进一步将不同横向空间距离、不同纵向空间距离、不同光谱波长、乃至不同时刻的散射光场等因素同时考虑，在一个更为广泛的时间和空间尺度范围内定义光学记忆效应，则有助于我们从更新的角度加深对相关问题的理解.在测量相应的系统点扩散函数时，并不局限于不同空间范围的PSF，也包括同一空间范围在不同时刻或者在不同频率光照下的PSF，因此，前述散斑自相关和散斑解卷积等基于光学记忆效应的散射介质成像方法也可能扩展到更大的时空范围.也就是说即使在多种因素的共同作用下，只要在考察区域范围内满足恢复成像要求的取值，则以往研究人员基于入射光场角度改变或者空间平移所提出的利用光学记忆效应实现散射成像的方法依然有可能适用.

其次，测量PSF时不再受单一因素影响，而是在多种因素综合作用下最终表现出的尺度缩放.尤其需要注意的是，存在多种影响因素，其在共同作用过程中，对考察区域PSF之间相关度的影响会出现此消彼长的现象，因此在研究散射介质成像的过程中，有可能充分利用这种影响因素之间的关联性，以便在不同时空域之间实现目标物体的成像.例如，通过改变照明光场的频谱特性可能得到目标物体沿纵向的空间尺度的分布情况，或者调节光源的随时间光场发射状态来获得各频段光波照射下目标物体的谱图，等等.同时，随着对光学记忆效应概念描述维度的扩大，原本在低维度描述体系下超出光学记忆效应范围的问题，有可能在高维度仍然属于同一记忆效应范围，因此可以用来解决扩大成像视场等瓶颈问题.

总之，研究如何扩大光学记忆效应的范围，可以为今后散射介质成像问题的研究带来新的提示，使散射系统成像特性的研究从孤立的局域的层面进入到关联的全域的高度，以便更能接触到散射介质成像的本质.同时，由于可以通过相关影响因素彼此消长来实现相关度的提高，这意味着在综合多种因素影响下会比单一因素可能得到更高的PSF相关度，进而有望开发出能够包含更多图像细节的成像技术，为探索光学记忆效应及散射成像技术开辟新的研究方向.

4 结论

本文在回顾散射介质成像领域中光学记忆效应概念的提出及所起重要作用的基础上，根据近年来相关研究成果，对原有光学记忆效应在概念上进行了拓展.光学记忆效应概念最初是基于入射光线旋转情况下观察到的散斑图案变化特性总结归纳得出的，并据此发展出许多具有一定效果的散射成像方法，但同时也存在大视场成像范围受限等问题.我们从分析散斑相关性的角度出发，将光学记忆效应概念定义为在不同横向空间距离、不同纵向空间距离、不同光谱波长、乃至不同时刻的散射光场等因素综合作用下的具有较高点扩散函数相关性的区域.我们将其称为广义光学记忆效应的概念，并且这一概念的拓展，将有助于全面描述点扩散函数时空特征，为散射介质成像技术的深入研究提供新的思路.