基于AOSO递进优化方法的车体抖振控制研究

王泽根，宫 岛，周劲松，孙 煜，李哲豪

（同济大学铁道与城市轨道交通研究院，上海 201804）

引言

高速动车组因其平稳舒适、方便快捷的特点，成为现今人们出行的主流交通工具。但随着运营时间的增加，某型动车组在线路上运行时出现了车体抖振问题，影响着车辆的运行安全。因此，分析动车组车体异常振动的成因以及解决问题的方法，成为维护动车组运营发展的重要任务。在对铁道车辆横向异常振动研究方面，Xia 等［1］基于小波包变换，提出一种车体低频异常晃动的在线检测方法。孙善超等［2］认为车辆运行中轮轨关系的不匹配会使转向架整体蛇行振型的阻尼因子过小，从而降低稳定性，导致车辆出现主频为5.7 Hz 的横向晃车现象，并提出通过调节轮对内侧距来改善晃车现象。叶一鸣等［3］认为钢轨交替不均匀侧磨、轨道轨向与水平复合不平顺是引发机车晃车的主要因素，并给出指导现场养修的预防措施。Qi 等［4］发现高速列车通过道岔时，由于轮轨接触关系改变，车轮踏面的等效锥度增加，导致转向架横向失稳，从而引发主频为7.1 Hz 的车身异常振动。并提出两种治理方案：减小轮缘后部之间的距离和优化悬挂参数可以有效减小转向架和车体的横向振动加速度，进而改善车身的晃动；通过钢轨打磨、车轮镟修等改善轮轨关系的措施［5-6］以及设计车体模态［7］，来缓解车体的异常振动。在垂向振动及控制方面，Wang 等［8］在研究低地板有轨车辆时，发现车体异常垂向振动是由车体的俯仰运动引起的，并将动态吸振器理论应用在铁路列车上，来减小车辆的异常垂向振动。此外，还有通过合理设计动态吸振器的参数来抑制车身弹跳和俯仰的低频振动［9］以及柔性车身的共振问题［10］。但对于特定情况的异常振动，还需根据实际情况深入分析来制定治理措施。

本文首先对某型动车组的在线试验数据进行分析，探究车体发生异常抖振的成因，然后提出一种融合解析优化和仿真优化的两级递进优化方法，对抗蛇行减振器的参数进行优化，来提高车辆运行的稳定性，从而控制车体的异常振动，并进行仿真及试验验证。

1 在线试验分析

根据对某型动车组的在线试验发现，车辆在运行中存在抖振现象并伴有转向架蛇行运动，该现象在运行速度超过120 km/h 且大踏面锥度状态下更为显著，威胁着车辆的运行安全。图1 为测量车体中部地板面横向振动加速度和构架横向振动加速度信号的传感器现场布置位置。车辆的在线试验记录了运行全程车体和构架振动加速度的时间历程，当振动加速度明显增大并且呈现谐波震荡趋势时，表明车辆发生抖振现象，振动主频为9.8 Hz，该时间段（里程段）定义为抖振段，反之未发生此现象的时间段（里程段）定义为非抖振段。本文在抖振段和非抖振段的测试数据中分别截取10 s 典型数据进行分析。图2 为典型抖振段与非抖振段的车体中部地板面横向振动加速度时间历程及幅频曲线，车辆运行时速为140 km/h。从图中可以看出，车辆发生抖振时车体的横向振动加速度会显著增大，且出现明显的谐波震荡，抖振主频为9.8 Hz，与该车车体菱形模态频率EMA（Experimental Modal Analysis）试验结果（10.04 Hz）接近。

图3 是与图2 对应的相同时刻下，转向架构架横向振动的时间历程及幅频曲线。可以看到，车体发生抖振时，转向架构架横向振动也呈谐波震荡趋势，说明转向架已经出现明显的蛇行运动，且主频为9.8 Hz。同时，时间历程结果还可以看出，转向架未达到失稳临界值［11-12］。据此可认为，抖振是一种车体菱形模态振动被放大并伴随转向架蛇行运动的整车异常振动现象。

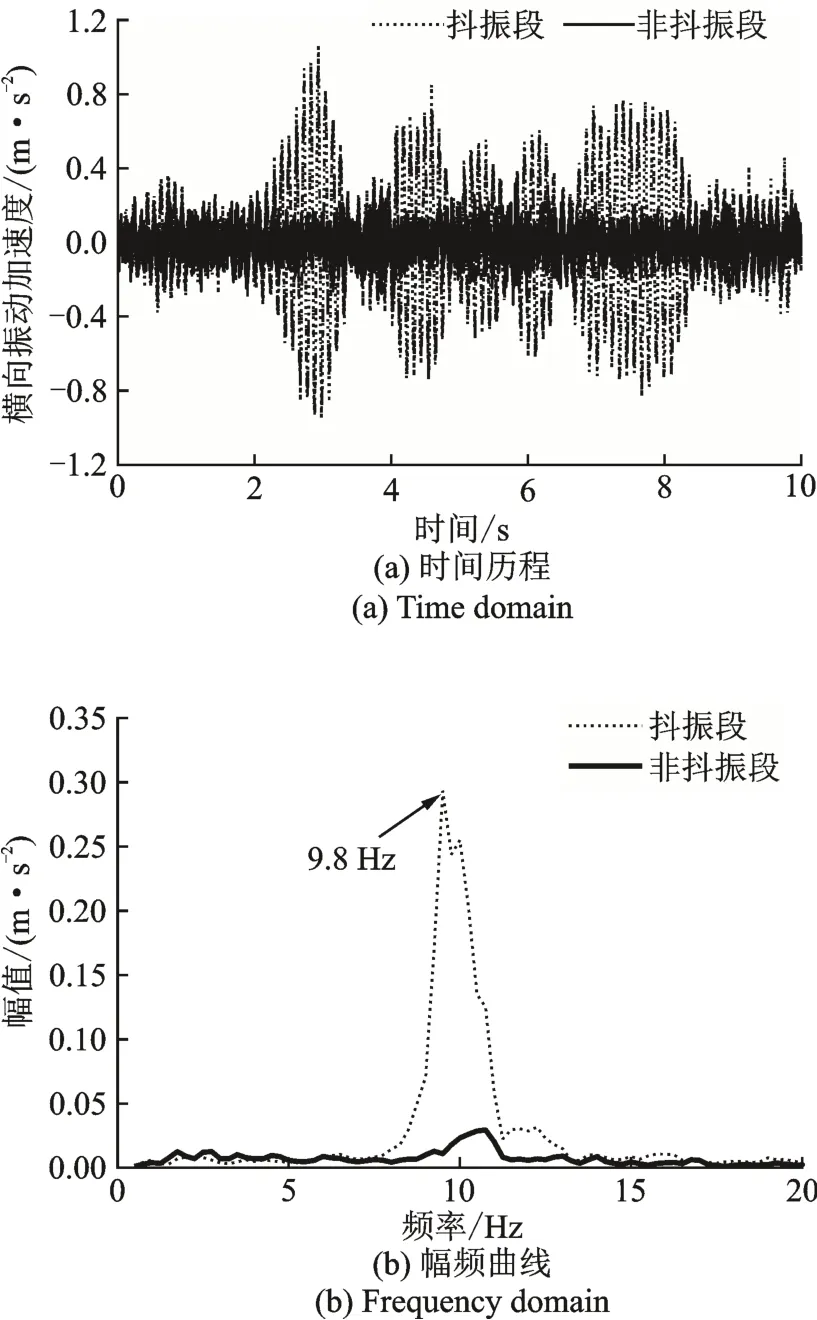
图2 车体中部地板面横向振动加速度Fig.2 Lateral vibration acceleration of the floor in the middle of the carbody

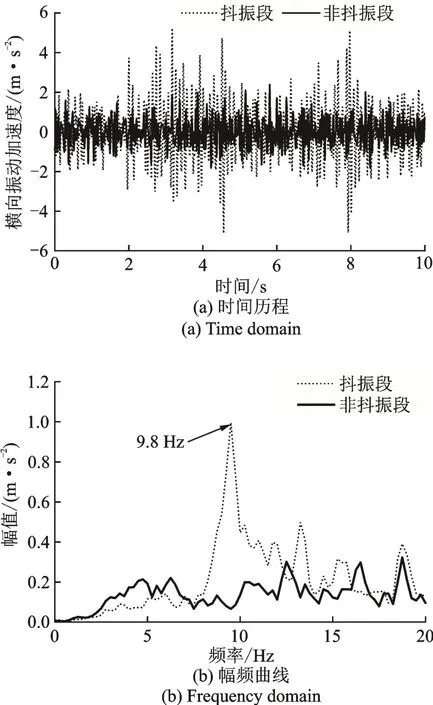
图3 构架横向振动加速度Fig.3 Lateral vibration acceleration of frame

图4 为实测车轮的轮轨接触关系，其中新车轮踏面等效锥度为0.103，磨耗轮踏面等效锥度为0.558。磨耗轮的运行里程为5×104km，还远未达到镟修规定的里程。经对比发现，磨耗轮存在一定程度的凹磨现象，轮轨接触点集中，所以车辆在轨道不平顺的激励下，致使轮轨接触发生变化，使得轮轨接触点移动至凹磨边界，此时车轮等效锥度瞬间增大，并导致转向架蛇行运动频率陡增。为抑制因转向架蛇行运动引发的整车异常抖振现象，本文通过优化悬挂参数来提高车轮磨耗状态下车辆的临界速度，进一步增加转向架蛇行运动稳定性裕量，来控制上述异常振动的发生。在车辆的悬挂元件中，抗蛇行减振器和一系定位刚度对临界速度的影响较大，但改变一系定位刚度又会对车辆通过曲线段的安全性产生一定影响。因此，为了提高车辆的临界速度同时对其他动力学性能不造成较大影响，将优化的对象确定为抗蛇行减振器。

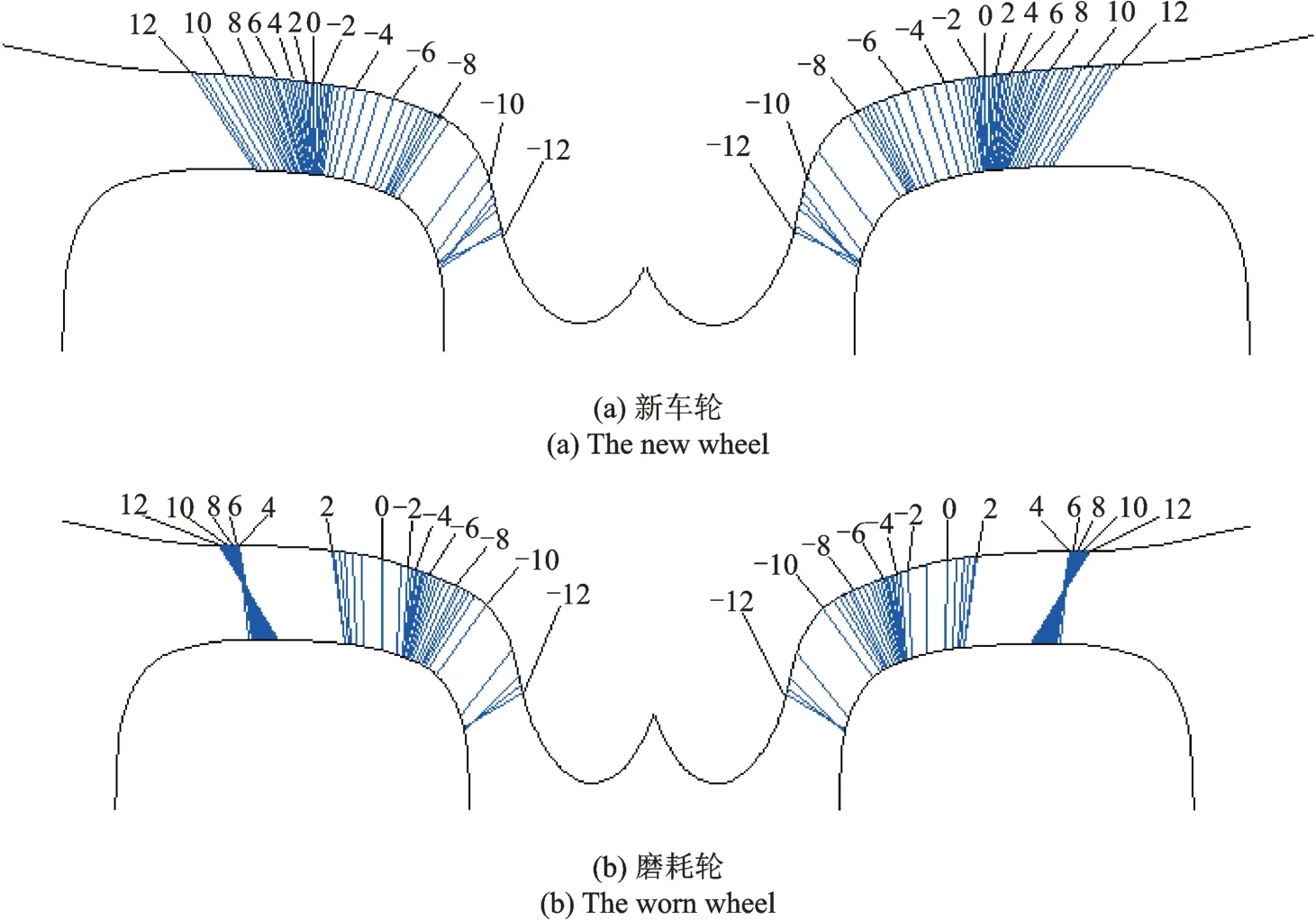
图4 轮轨接触关系Fig.4 Wheel-rail contact relationship

2 递进优化方法

本文提出一种融合解析优化和仿真优化的两级递进优化方法（AOSO），第一级解析优化（AO）可科学、高效地缩小各参数的优化范围，第二级仿真优化（SO）是在第一级优化基础上，对各参数再次进行细致优化，最终得到各参数精确的优化值，AOSO 可为多参数多目标优化问题的解决提供方法。该方法的实现过程如图5所示。

图5 递进优化方法（AOSO）Fig.5 Progressive optimization method（AOSO）

步骤一：明确目标问题。针对具体的工程优化问题，首先确定需要优化的参数和目标指标。为了改善磨耗轮状态下车辆的稳定性，并兼顾新车轮状态，将优化的参数确定为抗蛇行减振器的刚度和阻尼，优化目标为磨耗轮、新车轮状态下车辆的临界速度。

步骤二：解析优化。首先建立转向架稳定性解析模型，从理论计算角度来分析抗蛇行减振器参数对临界速度的影响规律，然后初步筛选出各参数的优化范围，为下一步，即步骤三中优化试验的制定提供便利。

步骤三：仿真优化。首先建立该型车的车辆动力学模型，然后在步骤二参数初步优化的基础上，制定优化试验方案，采用均值法和极差法对参数进行二次细致优化，进而得到精确的参数优化值。

步骤四：得到参数优化结果。根据步骤三的优化分析结果，最终确定满足多目标的各参数优化结果。

3 解析优化AO

3.1 转向架稳定性解析模型

为了研究抗蛇行减振器参数对临界速度的影响，构建如图6所示的刚性转向架解析模型，并将抗蛇行减振器简化为由弹簧与阻尼串联组成的Maxwell 模型［13-14］。轮对与构架刚性连接即一系定位刚度无穷大，以此来模拟转向架蛇行运动最为严重的情况，进而保证抗蛇行减振器参数筛选的准确性。其中m为转向架质量，J为转向架摇头惯量，ksx和ksy为二系纵向、横向刚度，csy为二系横向阻尼，keq和ceq为抗蛇行减振器等效刚度和阻尼，y为构架横向位移，φ为构架摇头角，f为横向/纵向蠕滑力系数，v为车辆运行速度，l，l1和l2为轴距、二系空簧、抗蛇行减振器横线间距之半，xs为活塞杆位移，b为轨距之半，λ为轮对的等效锥度，r0为车轮名义滚动圆半径，ya1和ya2为第一、二轮对的横向激励。

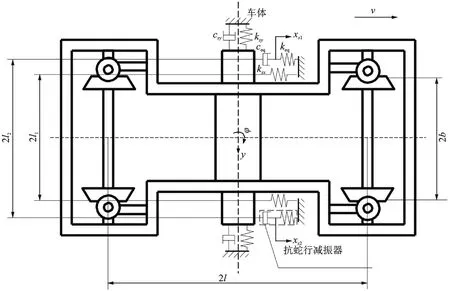
图6 刚性转向架解析模型Fig.6 Analytical model of rigid bogie

该模型的建立基于以下假设：（1）轮对和构架均为刚体；（2）构架为对称结构，两侧抗蛇行减振器的活塞杆位移一致；（3）整体振动的位移和速度相对较小，二系悬挂的刚度和阻尼均在线性范围内工作；（4）依据Kalker 线性轮轨接触理论［15］，假设横向和纵向蠕滑力系数相等。

根据牛顿第二定律［16-18］，建立此刚性转向架系统的运动微分方程为：

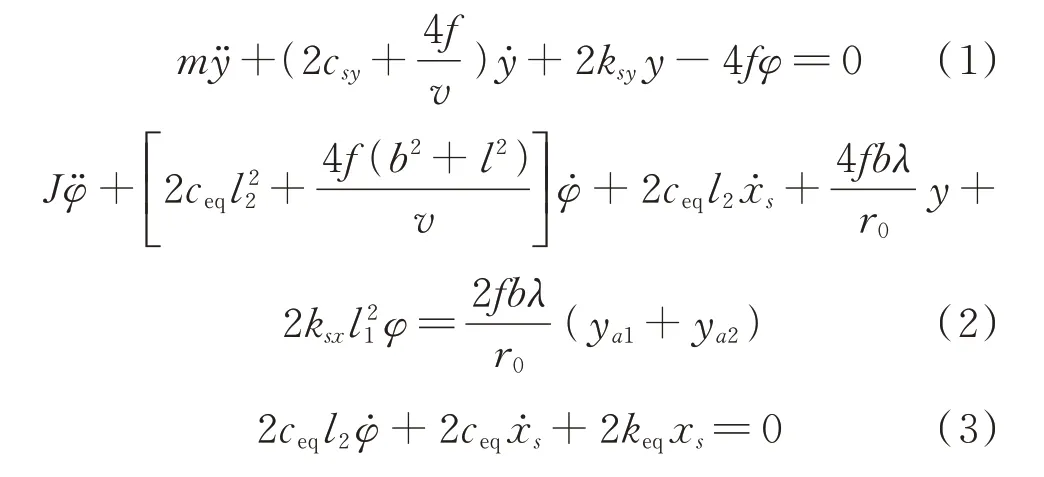
将式（1）～（3）转换成矩阵形式：

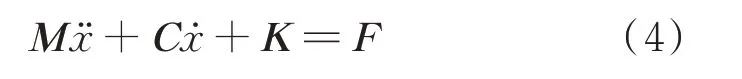
式中M为质量矩阵，C为阻尼矩阵，K为刚度矩阵，F为轨道不平顺的激振力矢量。

对式（4）左侧作拉普拉斯变换，使其行列式为零，得：

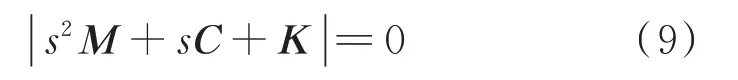
忽略抗蛇行减振器的质量，依据Hurwitz 稳定判据［19-20］建立的五阶特征多项式为：

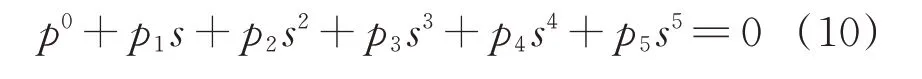
其中各阶系数分别为：

根据Hurwitz 稳定判据，可直接从稳定性临界条件Δ5=0 得到转向架系统的临界速度，即：

一般而言，对于高于五阶的多项式的解析解是存在一定问题的。所以本文采取以下方法：式（10）特征多项式应该至少有一个虚根是转向架系统达到的临界状态。将该约束作为已知条件加入式（10），将特征多项式的虚部和实部分别设为零，得：

将式（13）中的三项分别代入，可得到三个最高阶为二阶和三阶的求解转向架系统临界速度的方程：

求解式（14）～（16），v的最小值即为该转向架系统的临界速度。

3.2 解析优化分析

将表1 中的参数代入解析模型中求解，其中抗蛇行减振器的等效刚度和等效阻尼的取值范围是由实际可制造的成品确定，车轮踏面等效锥度值是按照实测车轮与CHN60 轨实际匹配来给定的。然后分析抗蛇行减振器参数变化对临界速度的影响规律，最后得到能够提升磨耗轮状态下车辆稳定性的抗蛇行减振器参数优化范围。

表1 车辆动力学参数Tab.1 Vehicle dynamic parameters

图7 和8 分别为新车轮状态下抗蛇行减振器参数对运行稳定性影响的趋势图及等高线图。分析可知，抗蛇行减振器等效刚度在0～5 MN/m 范围内，临界速度随抗蛇行减振器等效阻尼的增加而提升，然后逐渐达到恒定状态，等效刚度越大，临界速度恒定值越高；等效刚度在6～20 MN/m 范围内，临界速度随等效阻尼的增加而持续上升，且在等效刚度为7～15 MN/m 范围内（尤其10 MN/m 附近），临界速度随等效阻尼的增加而显著上升，均高于前、后等效刚度区段的临界速度。

图7 新车轮状态下抗蛇行减振器参数变化对稳定性的影响Fig.7 The influence of the parameters of the anti-yaw damper on the stability of new wheel

图9 和10 分别为磨耗轮状态下抗蛇行减振器参数对运行稳定性影响的趋势图及等高线图。分析可知，临界速度随抗蛇行减振器等效阻尼的增加呈现先增加后逐渐趋于恒定的趋势，并且等效刚度越大，所对应的临界速度恒定值越高。

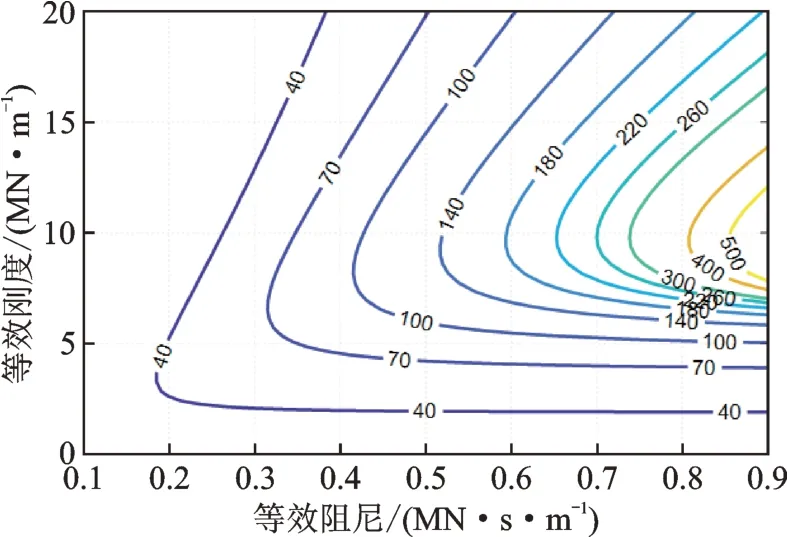
图8 新车轮状态下临界速度等高线图Fig.8 Contour diagram of critical speed of new wheel

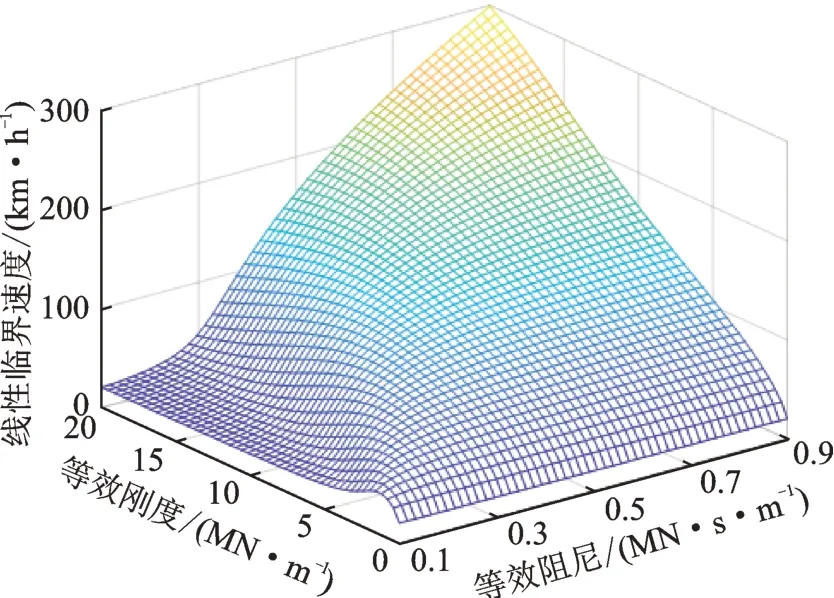
图9 磨耗轮状态下抗蛇行减振器参数变化对稳定性的影响Fig.9 The influence of the parameters of the anti-yaw damper on the stability of abrasion wheel

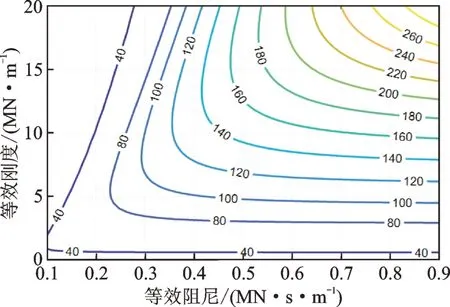
图10 磨耗轮状态下临界速度等高线图Fig.10 Contour diagram of critical speed of abrasion wheel

对上述两种踏面状态进行比较发现，随着车轮磨耗的增加，临界速度将会下降，进而降低车辆运行的稳定性，使得大踏面锥度状态下的车辆在较高速度运行时出现蛇行运动，引发车体的抖振。为了提升磨耗轮状态的稳定性，综合磨耗轮和新车轮两种状态下解析计算的结果，筛选出参数经过AO 确定的优化范围为等效刚度16～20 MN/m、等效阻尼0.5～0.9 MN·s/m。

4 仿真优化SO

4.1 车辆动力学模型

根据该型车的动力学参数，在多体动力学软件SIMPACK 中建立如图11所示的刚柔耦合车辆动力学模型［21-22］，模型包括1 个车体、2 个构架、4 个轮对、8 个轴箱以及各种减振元件。考虑车体弹性，使其具备真实车体的振动模态信息。相较于车体而言，构架、轮对、轴箱的弹性变形均较小，故考虑为刚性。抗蛇行减振器具有卸荷特性，因此需将等效阻尼考虑为卸荷速度和卸荷力。表2所示为车体模态缩聚结果与试验模态结果的对比，可以看出仿真模型与试验模型的模态频率的误差均小于5%，模态缩聚结果合理。

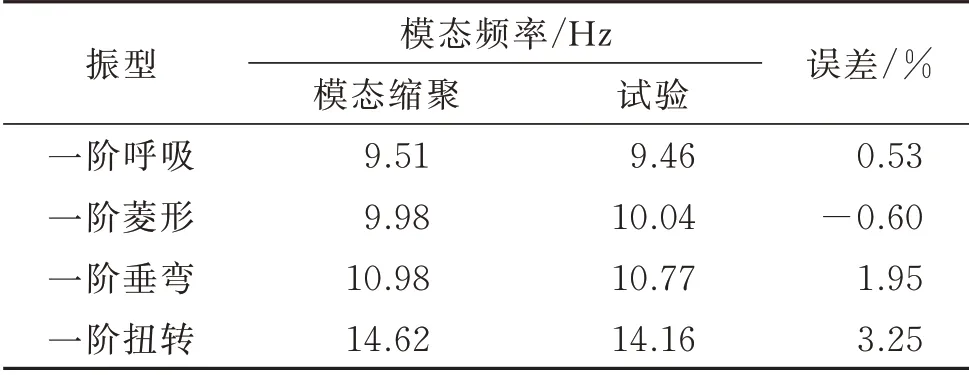
表2 车体模态缩聚结果与试验模态结果对比Tab.2 Comparison of modal polycondensation results with experimental mode results

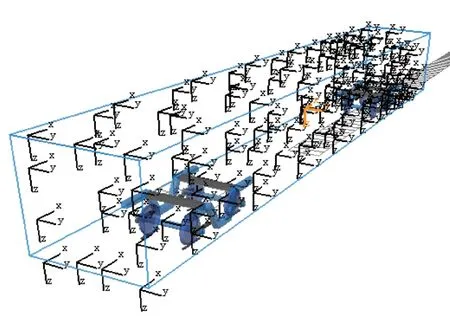
图11 刚柔耦合车辆动力学模型Fig.11 Rigid and flexible coupling vehicle dynamics model

仿真时新车轮踏面、磨耗轮踏面、轨道不平顺均采用实测数据，车辆运行速度为140 km/h。图12 为通过车辆动力学模型得到的车体抖振复现数据，可以看出，抖振时车体的横向振动加速度幅值显著增大，且呈谐波变化，抖振主频为9.84 Hz，仿真结果与车辆在线试验一致，表明所建动力学模型是准确的。

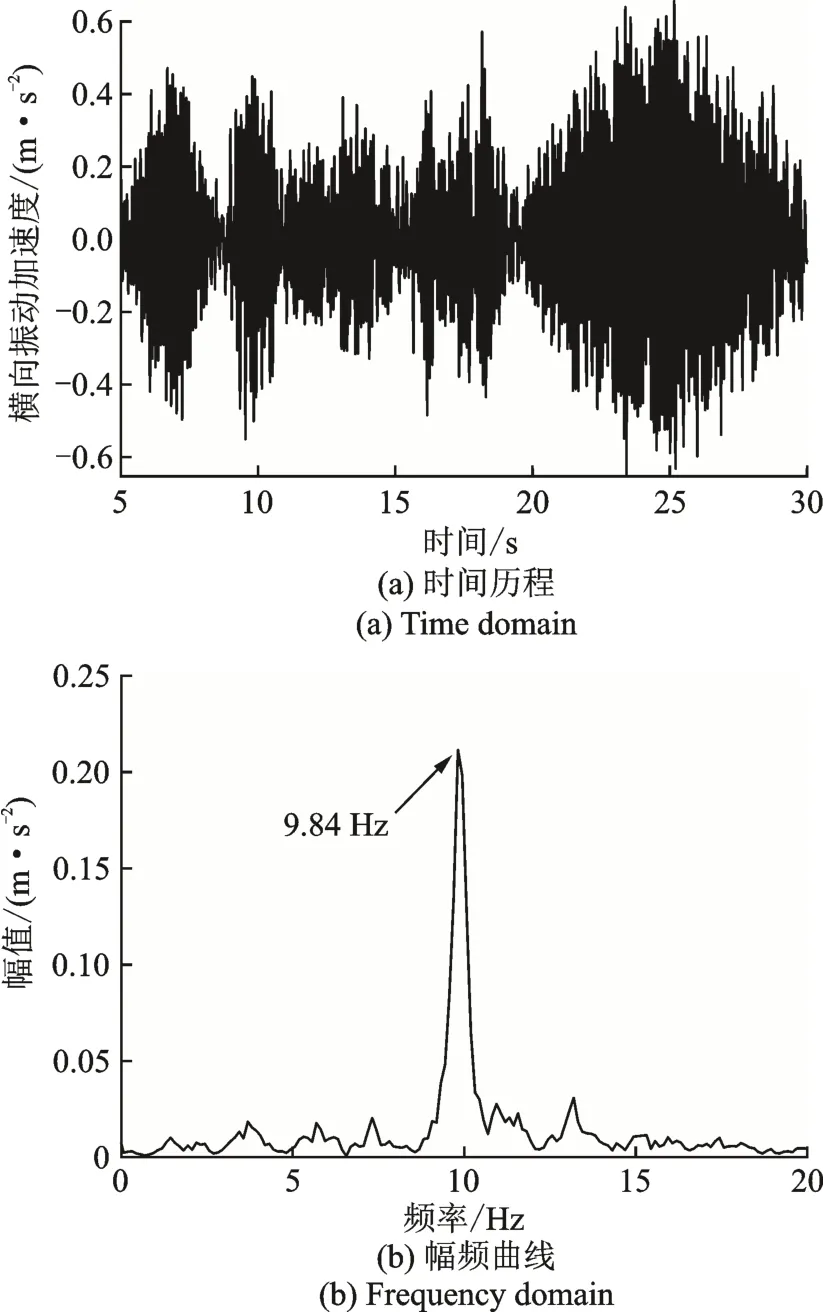
图12 抖振段车体横向振动加速度仿真结果Fig.12 Simulation results of carbody lateral vibration acceleration of chattering section

4.2 仿真优化分析

根据解析优化确定的参数范围和表3 抗蛇行减振器的原始参数值，综合确定表4 抗蛇行减振器等效刚度、卸荷速度以及卸荷力的各水平值，可以看出每个参数有5 种变化水平。接下来制定表5所示的优化试验，表中A，B 和C 分别代表抗蛇行减振器的等效刚度、卸荷速度以及卸荷力。优化试验一共开展25 组，每组试验中各参数都有对应的水平。然后分别对新车轮和磨耗轮两种状态的车辆动力学模型开展优化试验，记录每组试验的结果。

表3 抗蛇行减振器参数Tab.3 Parameters of anti-yaw damper

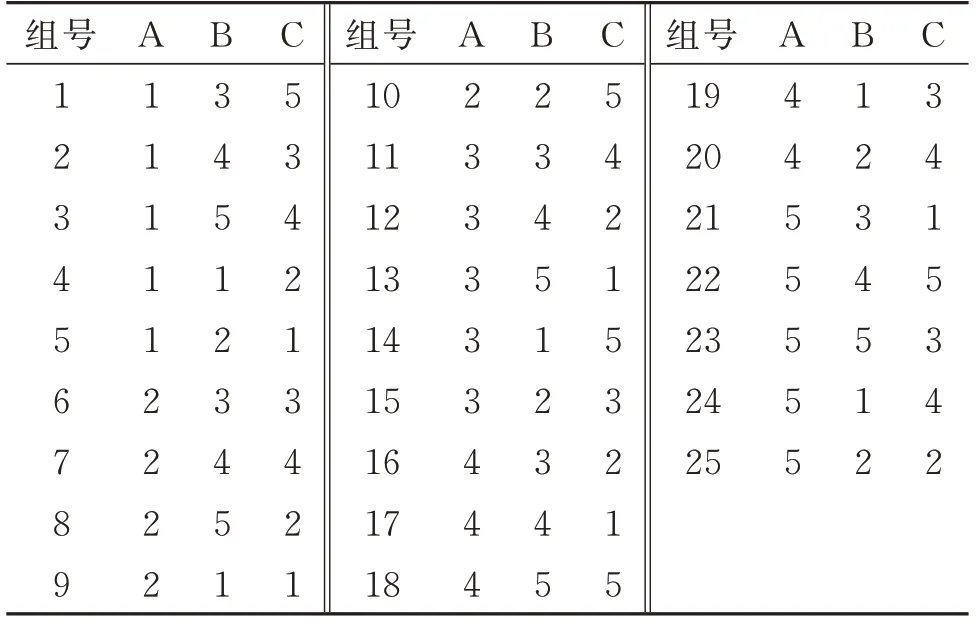
表5 优化试验Tab.5 Optimization test

优化试验的结果需依次运用均值法和极差法来处理。均值法是按照表5所示的25 组优化试验，对同一参数所对应同一水平的5 组试验结果做均值处理，使得结果涵盖另外两个参数变化带来的影响，更加真实合理。图13（a）和（b）分别为新车轮及磨耗轮两种状态下经均值处理的优化试验结果。从结果中可以看到临界速度随各参数变化的总体趋势。然后通过极差法来筛选最优方案，极差法首先求取各参数在5 个水平变化的极差，然后按极差的大小对三个参数赋予优先级顺序，极差大的意味着该参数对临界速度影响大。再根据均值处理结果写出新车轮和磨耗轮两种状态下最高临界速度所对应的参数水平，即最优序列。表6 为极差法处理的结果，可以看出，抗蛇行减振器的等效刚度对临界速度的影响要小于卸荷速度和卸荷力对临界速度的影响，而且两种车轮状态的最优序列基本一致。为了更显著提升磨耗轮状态的临界速度，避免车辆在大踏面锥度状态下发生蛇行失稳，再加上可制造抗蛇行减振器成品阻尼的限制，最终确定抗蛇行减振器参数优化结果为等效刚度17 MN/m、卸荷速度0.01 m/s、卸荷力9000 N。

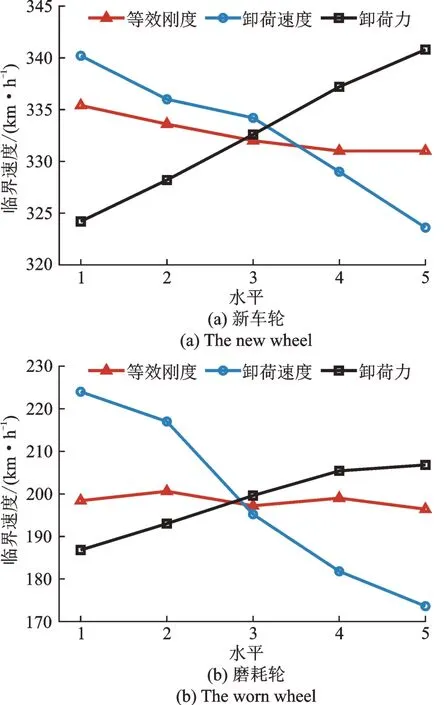
图13 均值法处理结果Fig.13 Results of the mean method

表6 极差法处理结果Tab.6 Results of the range method

表7 为两种踏面状态下，抗蛇行减振器参数优化前后所对应的临界速度，可见优化后两种踏面状态的车辆临界速度均得到提升，新车轮状态下临界速度较原参数工况提高了4.83%，磨耗轮状态下临界速度较原参数工况提高了19.68%，磨耗轮状态的临界速度提升明显。

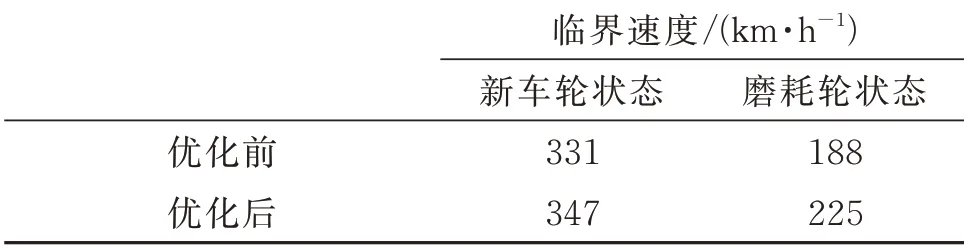
表7 优化前后临界速度对比Tab.7 Comparison of critical velocity before and after optimization

5 验证分析

5.1 仿真验证

图14 为抗蛇行减振器参数优化前后抖振段的仿真对比，仿真时车辆运行速度为140 km/h。可见优化后车体的横向振动加速度明显减小，9.84 Hz 的主频幅值也大幅度降低，车体的异常抖振得到明显改善。通过对抗蛇行减振器参数的优化，提高了车辆的运行稳定性裕量、改善了车辆运行中车体的抖振现象。

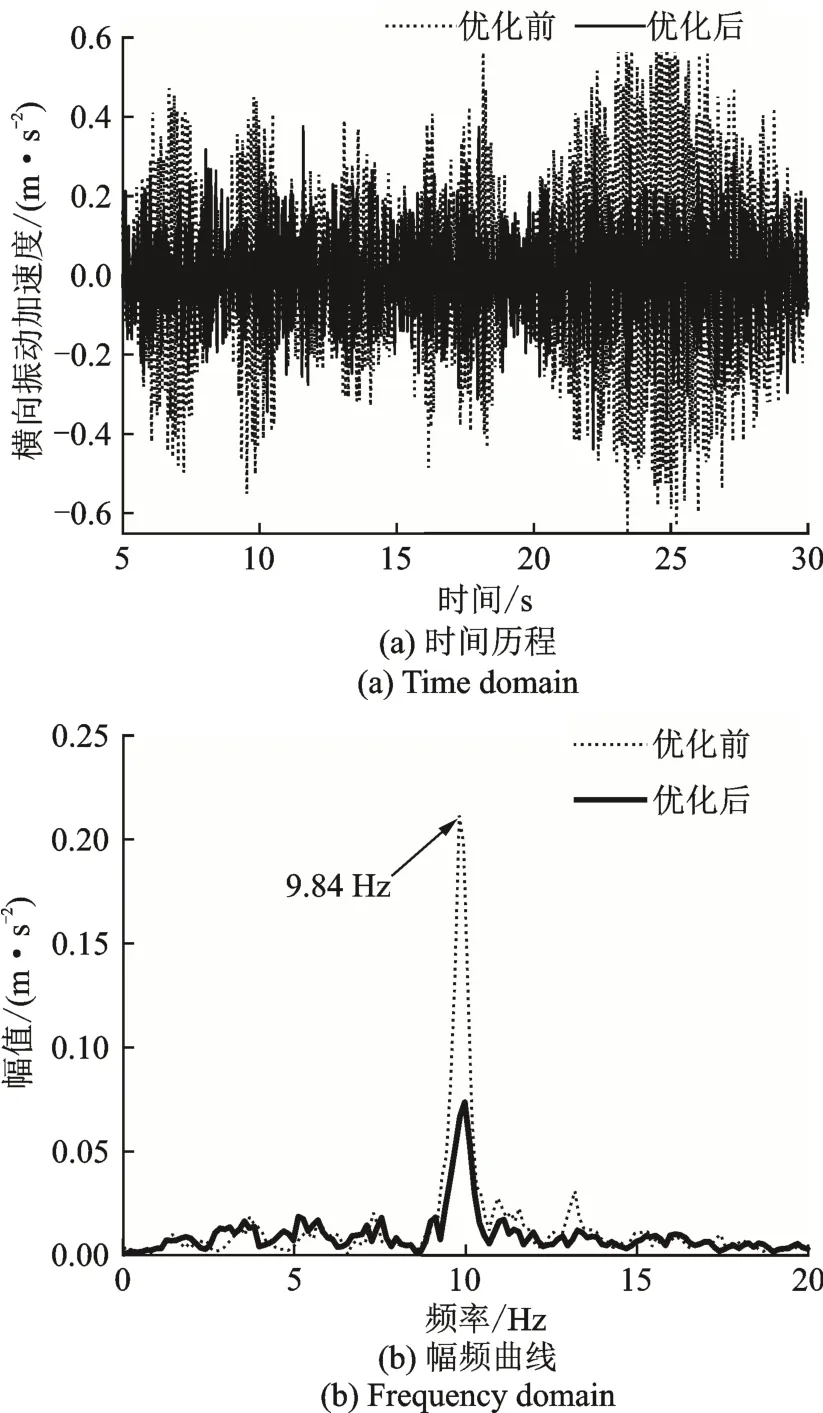
图14 抖振段车体横向振动加速度优化前后对比Fig.14 Comparison of carbody lateral vibration acceleration of chattering section before and after optimization

5.2 试验验证

为了验证抗蛇行减振器参数优化后的实际效果，给车辆更换优化后的抗蛇行减振器，然后进行车辆线路测试。图15～17 分别为车辆以120，140，160 km/h运行时，抖振段在抗蛇行减振器参数优化前后的对比，同样观察指标为车体中部地板面横向振动和构架横向振动的时间历程及幅频曲线。从结果可以看出，抗蛇行减振器参数优化后，车体抖振的幅度显著减小，抖振主频9.8 Hz处的幅值也明显下降。构架横向振动的幅值也显著减小，已无明显的蛇行运动，主频9.8 Hz处的幅值也明显下降。因此可得，通过对抗蛇行减振器的参数进行优化，车体抖振得到控制和改善。

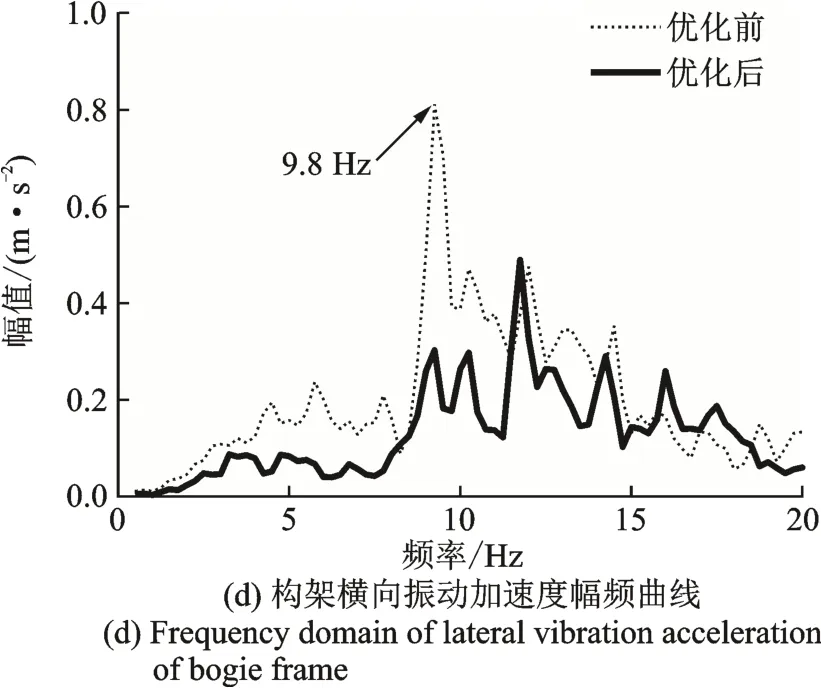
图15 120 km/h 时试验测试数据Fig.15 Test data at 120 km/h

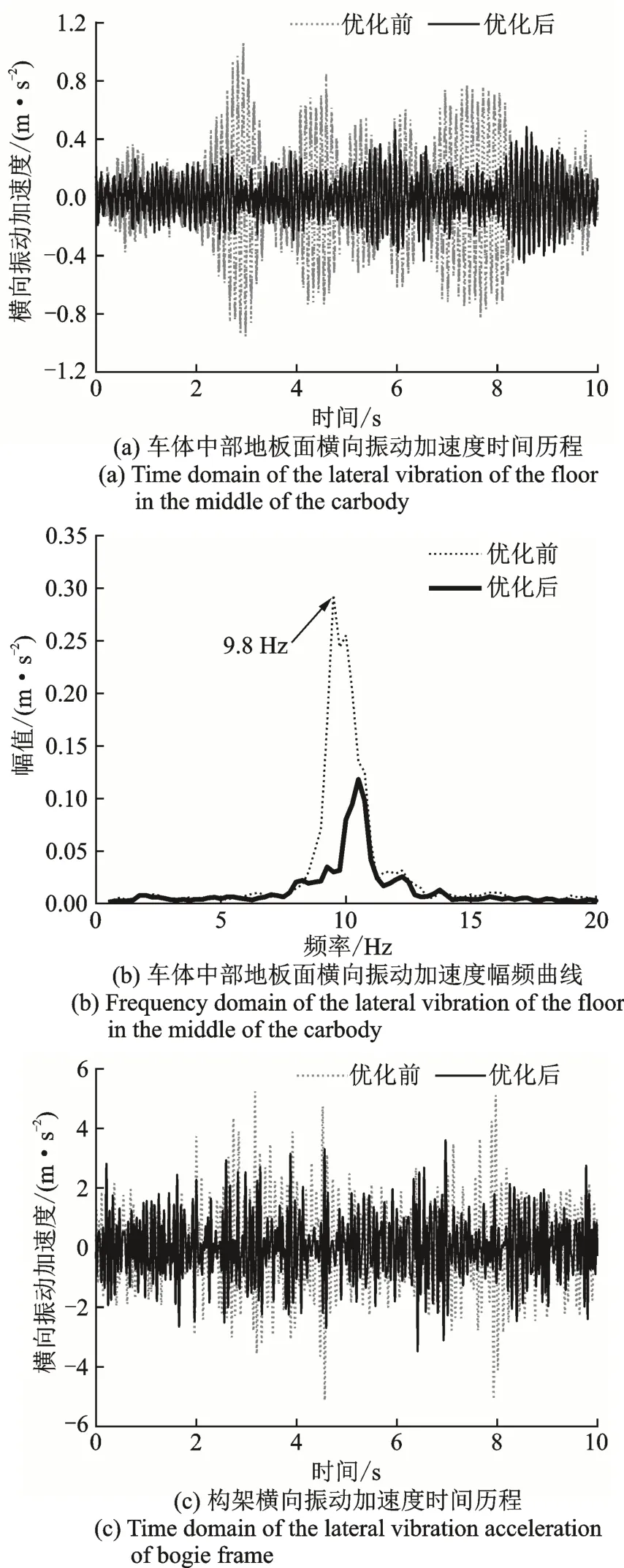
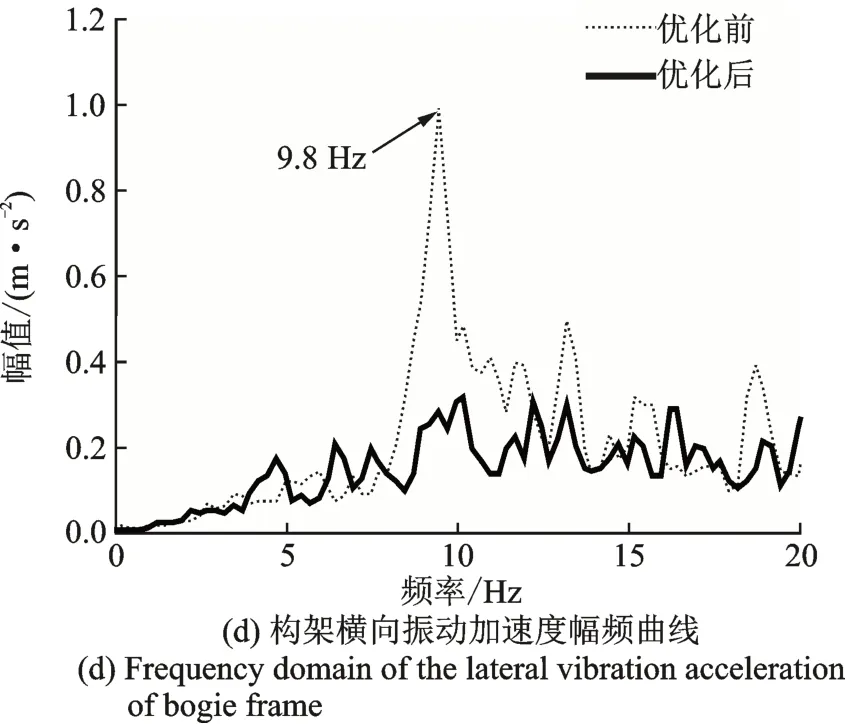
图16 140 km/h 时试验测试数据Fig.16 Test data at 140 km/h

图17 160 km/h 时试验测试数据Fig.17 Test data at 160 km/h

6 结论

本文针对某型动车组在运行中出现的车体抖振问题展开研究，分析了车体抖振的成因，并提出了控制车体抖振的方案，最后将治理方案在试验中得到验证。结论如下：

（1）通过对车辆在线试验的分析发现，较高速度运行时大踏面锥度状态的转向架蛇行运动的频率上升，稳定性下降，转向架蛇行运动的频率与车体菱形模态接近从而引发车体的抖振。

（2）为了提升车辆稳定性裕量，提出一种融合解析优化和仿真优化的两级递进优化方法（AOSO），对抗蛇行减振器的参数进行优化，最终优化结果为等效刚度17 MN/m，卸荷速度0.01 m/s，卸荷力9000 N。优化后新车轮状态下临界速度为347 km/h，较原工况参数提高了4.83%，磨耗轮状态下临界速度为225 km/h，较原工况参数提高了19.68%，磨耗轮状态的临界速度提升明显。

（3）仿真验证发现，抗蛇行减振器参数优化后，车体抖振主频处的振动能量被明显衰减。

（4）试验验证发现，车辆在更换优化后的抗蛇行减振器后，车体抖振的幅度显著减小，抖振主频9.8 Hz 处的幅值也明显下降，转向架已无明显的蛇行运动。因此，该优化方案使车体抖振问题得到了控制和改善。