桥梁耦合极值应力的贝叶斯动态预测
2022-07-26王佐才丁雅杰孙晓彤
戈 壁,王佐才,2,辛 宇,3,李 舒,丁雅杰,孙晓彤
(1.合肥工业大学土木与水利工程学院,安徽合肥 230009;2.土木工程防灾减灾安徽省工程技术研究中心,安徽合肥 230009;3.安徽省基础设施安全检测与监测工程实验室,安徽合肥 230009;4.清华大学合肥公共安全研究院,安徽合肥 230601)
引言
随着桥梁健康监测系统在实际工程中的普及,系统能够实时监测桥梁结构在服役期内的响应及变形[1-3]。其中,在环境及荷载作用下结构内部产生的应力反映了结构局部的受力状态,同时也是结构安全运营状态的重要指标之一。因此,应力监测在桥梁健康监测系统中具有十分重要的地位。应力监测可分为监测数据的收集和应用两个部分。经过几十年的研发,数据收集技术都已相对成熟[4-6]。目前国内外学者的研究主要集中在基于历史监测数据的应用方面,并在桥梁结构损伤识别[7-9]、荷载效应分析建模[10]、模态参数识别[11]等方面取得了一定的成果。然而,在基于桥梁极值应力监测数据的结构安全性能评估与预测方面还有待发展。桥梁极值应力蕴含着结构安全性能的重要信息,对极值应力进行分析以及动态预估,不但能够动态、直观地反映在役桥梁运营状况下的极值应力状态,为桥梁结构的维护与养护提供重要依据,而且能够为桥梁的动态安全性能评估提供理论依据。因此,如何合理地利用海量历史监测数据,实现结构响应的动态预估是结构健康监测目前亟需解决的关键问题。
目前,基于实际监测数据对结构响应进行动态预估已经有了一些研究。例如,冯海月等[12]基于广义Pareto 分布提出了一种改进的独立风暴法,可较好地预测车辆荷载效应。阳霞等[13-14]改进了广义Pareto 分布模型的阈值选取方法,并可利用实际监测数据建立具有一定规律的概率统计模型。研究表明改进后的概率统计模型能够更好地拟合出由车辆荷载引起的桥梁应变右尾分布,结合极值统计理论能够对桥梁剩余服役期内的应变极值进行估计。Fan 等[15]提出可利用极值应力监测数据以及高斯混合粒子滤波器实现桥梁极值应力的动态预测。但是,由于极值应力是多种荷载效应的耦合,直接对耦合监测数据进行拟合以及动态预估,其效果并不理想。近年来,由于贝叶斯动态模型可结合监测数据的客观信息和主观信息,能够对桥梁极值应力进行有效预测,使该方法得到了长足的发展[16-17]。Ni 等认为在役桥梁由于承受了多种荷载才导致应变/应力响应数据结构的多模态性。为了更好地预测耦合极值应力,分别提出了一种具有较强非平稳动态过程建模能力的贝叶斯动态线性模型[18]和一种参数贝叶斯混合模型[19]。通过试验验证,改进后的模型对极值应力的预测精度具有一定程度地提高。Liu等[20]考虑到监测得到的耦合极值应力是非平稳数据与平稳数据的耦合,提出了一种利用局部多项式理论建立的贝叶斯动态线性趋势模型。该模型能有效地减小监测数据中非平稳趋势项对预测结果的影响,并随着预测模型参数的更新,桥梁耦合极值应力的预测结果越来越合理。樊学平等[21]则将桥梁耦合极值应力简单分为具有趋势性的温度荷载效应和具有随机性的车辆荷载效应并提出了基于解耦极值应力的动态耦合线性模型。模型首先使用简单的移动平均法数据解耦,再分别建立贝叶斯动态耦合线性模型并进行极值应力预测分析。樊学平等[22]认为由于监测数据具有动态性、随机性以及周期性等特点,因此可利用Fourier 函数对初始应力状态数据进行回归分析,进而运用Fourier 动态线性模型并对桥梁极值应力进行预测。从上述研究可以看出,基于贝叶斯方法的动态模型能够对桥梁极值应力进行动态预测,并且利用解耦极值应力数据,可使预测模型精度进一步提升。
由于桥梁耦合极值应力主要受到温度荷载效应、车辆荷载效应和风荷载效应等的影响,因此桥梁极值应力监测数据的解耦方法通常按照所受荷载类别进行解耦并分类,这就使得解耦数据仍可能是多阶模态响应的耦合。这样,利用解耦数据建立的贝叶斯动态模型依然存在着模型相对复杂,不能很好地体现桥梁极值应力周期性、随机性等数据特点的问题。为了解决上述问题,本文引入了Hilbert 信号分解以及解调技术,对数据进行解耦。该方法不但能够对具有密集模态与频率叠混的非平稳结构响应信号进行有效分解,而且能够很好地保存信号幅度、频率和相位的信息[23-25]。同时,在得到单分量极值应力数据后,即可利用Hilbert 信号解调技术,回归得到状态变量函数的参数,建立单分量极值应力数据的Hilbert 动态线性模型(Hilbert Dynamic Linear Model,HDLM)。随后,利用贝叶斯方法对模型进行概率递推,实现单分量极值应力的动态预测。将各阶单分量极值应力预测值进行相加即可得到桥梁耦合极值应力的动态预测值。最后,利用在役桥梁一年的监测数据对本文所提方法的有效性进行了验证。
1 桥梁耦合极值应力的动态预测
桥梁健康监测系统在长期运营期间可以监测大量的应力信息,而结构的应力响应则反映了诸多荷载(如温度荷载,车辆荷载,风荷载等)作用下结构的内部特征。因此,桥梁结构的应力响应具有复杂的耦合性。为了更好地动态预测桥梁耦合极值应力,本文首先建立了单分量极值应力的HDLM,进而提出了BHDLM。其中,HDLM 由监测方程与状态方程组成,状态变量表示了监测数据的变化趋势,而状态方程则描述了状态变量如何随时间变化,监测方程描述了监测变量与状态变量之间的关系。其中,预测模型的主要流程如图1所示。
从图1 流程图中可以看出,在数据解耦过程中,定义时间区间(t-1,t]内,监测的最大应力为桥梁耦合极值应力Yt,并将监测得到的极值应力数据视为一个时间序列。在得到Yt后,首先利用了Hilbert信号分解技术对数据进行解耦[23-26],得到有限多个具有单一频率成分的单分量极值应力数据yi,t。随后,基于Hilbert 平方解调算法(Hilbert Square Demodulation,HSD)回归得到各阶单分量极值应力数据yi,t的HDLM。一旦建立了单分量极值应力的HDLM,即可通过贝叶斯方法对模型中的参数实现概率递推,实现对极值应力的动态预测,进而可得到桥梁耦合极值应力的动态预测结果。
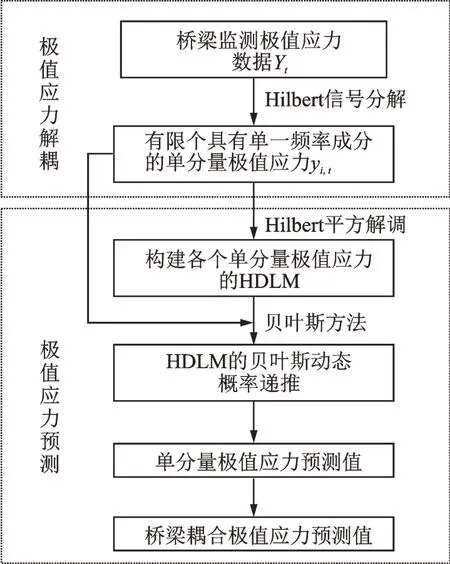
图1 桥梁耦合极值应力预测模型流程图Fig.1 The flowchart of the prediction model for bridge coupled extreme stress
2 单分量极值应力的HDLM 及参数确定
2.1 桥梁极值应力解耦
直接利用耦合极值应力进行建模与预测,不但增加了极值应力以及预测模型的复杂性,而且不利于应力预测的精度[20-21]。因此,为了减小监测数据的复杂性,满足建立预测模型的需要,对极值应力进行解耦应是HDLM 建模过程中的必要步骤。
在以往的研究中,桥梁耦合极值应力被认为是多种荷载效应的耦合,因此解耦过程中通常按荷载效应类型进行分类。一般利用简单移动平均、二次移动平均等拟合算法,即可得到结构监测应力的趋势项。趋势项的均值可看作结构自重荷载效应,而除去均值的趋势项因其具有较为明显的周期性,可认为是环境温度作用下的荷载效应。监测数据与趋势项的差值则被认为与车辆荷载效应和风荷载效应相关。可以看出上述解耦过程虽然步骤简单、便于实现,但过程中存在着经验成分,因此解耦过程并不十分充分。
根据模态叠加理论,结构的位移响应可表示为各阶模态贡献之和。如果只考虑结构某一方向的正应变,则应变与位移之间存在如下关系式:
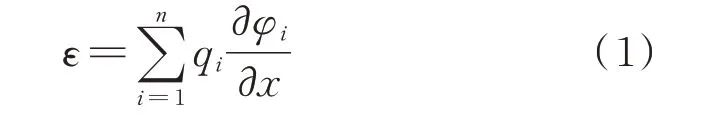
式中ε为正应变;φi为第i阶的位移模态振型;qi为模态坐标。而应力与应变在一定的比例极限范围内可视为线性关系。则Yt同样可以表示为具有n个有效频率ωi(i=1,2,…,n)成分耦合的实数时间序列。为了能够充分解耦,得到具有单一频率成分的单分量极值应力数据。本文提出利用Hilbert 信号分解算法对桥梁耦合极值应力进行分解[23-26]。一旦确定了Yt中的频率,即可利用Hilbert 变换的信号分解算法对Yt进行解耦,分解成n个具有单一频率的单分量成分yi,t(i=1,2,…,n)。则极值应力Yt可进一步表示为:

2.2 单分量极值应力解调
在利用Hilbert 信号分解算法将桥梁耦合极值应力Yt分解为有限多个单分量极值应力yi,t后,可进一步利用HSD 算法对yi,t进行解调,回归得到状态变量θi,t的函数。HSD 算法是一种针对具有单一频率成分数据的解调算法,其原理可简单概述如下[27]:
假设单分量极值应力数据yi,t的回归函数θi,t可简化为:
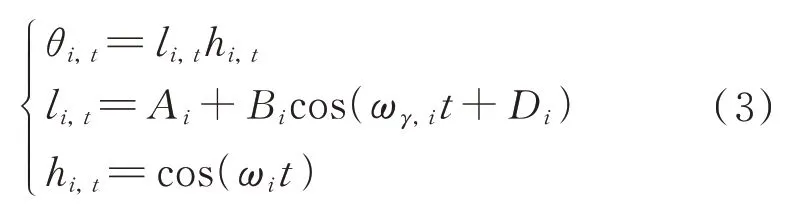
式中Ai,Bi,Di,ωγ,i以及ωi均为回归系数。首先,构建yi,t的解析信号Zi,t:
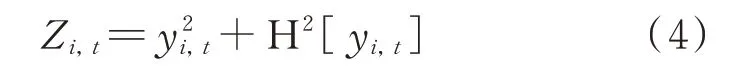
式中 H[·]为Hilbert 变换算子。则回归函数θi,t中的li,t可表示为:

联立公式(3)和(5),可进一步得到hi,t:

其中,为了减小单分量极值应力数据中噪声以及解调误差对回归函数θi,t的影响,可对公式(5)和(6)作进一步优化[27]。则回归系数Ai可认为是解调结果li,t的均值。li,t中的相位函数ωγ,it+Di可通过下式得到:
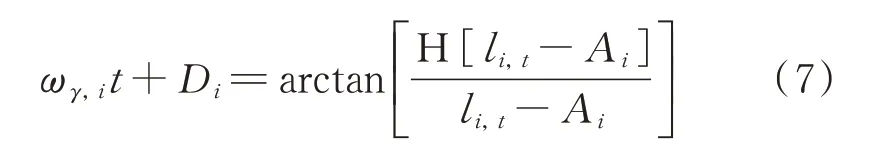
其中,系数ωγ,i可通过对相位函数求导得到,进而可回归得到Di。结合公式(5)和(7),回归系数Bi可表示为:

而hi,t中的相位函数ωit可表示为:

再对相位函数进行求导可得到回归系数ωi。
2.3 单分量极值应力的HDLM
根据公式(3)~(9),可得到各阶yi,t的单分量极值应力回归函数θi,t。则θi,t+1的表达式可由下式得到:
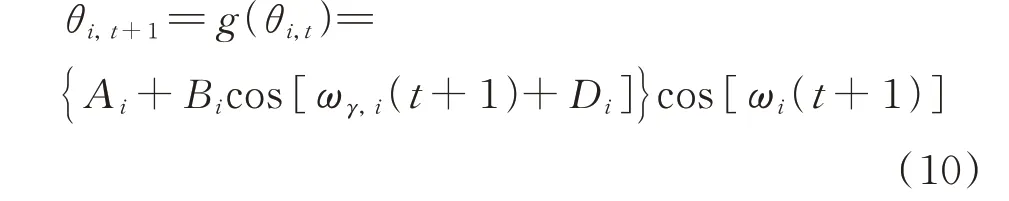
式中g(·)表示非线性函数。可以看出,状态变量随时间呈非线性关系。利用公式(10)可得到的历史监测应力数据的动态非线性模型。然而,由于贝叶斯方法更适用于线性模型,因此在得到动态非线性模型后往往需要进行线性化处理[28]。本文利用Taylor 级数展开技术,将g(θi,t)在初始状态数据的期望值M1,t附近处展开,即可得到公式(10)对应的线性函数:
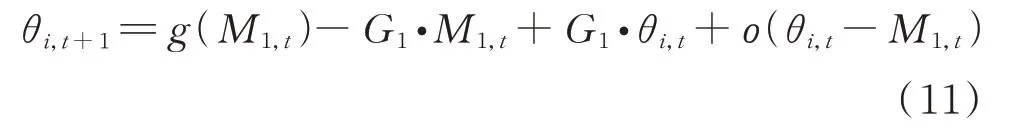
其中,初始状态数据可利用Hilbert 信号分解算法得到,则初始状态数据期望值M1,t可由数据的均值近似得到;为已知项,且与θi,t无关;о(θi,t-M1,t)为g(θt)在M1,t处展开的高阶项。公式(11)可进一步改写为:
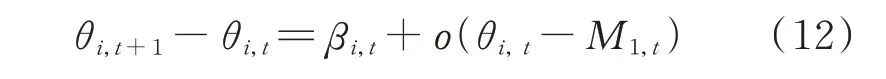
式中θi,t+1-θi,t为状态数据的一阶差分;βi,t=g(M1,t)-G1·M1,t+(G1-1)θi,t。通过公式(11)和(12)可以看出,状态t+1 时刻的状态变量θi,t+1不仅和前一时刻的θi,t有关,也可能与状态数据的一阶差分变量βi,t有关。考虑βi,t只与前一时刻的一阶差分变量βi,t-1有关,并忽略公式(11)和(12)中的高阶项,桥梁单分量极值应力的Hilbert 动态线性状态方程可表示为:
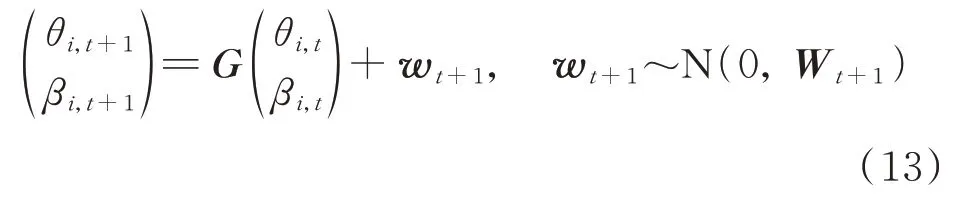
模型误差方差Wt+1无法直接从状态数据中得到,可根据初始状态数据的方差Ct近似计算得到[21]:
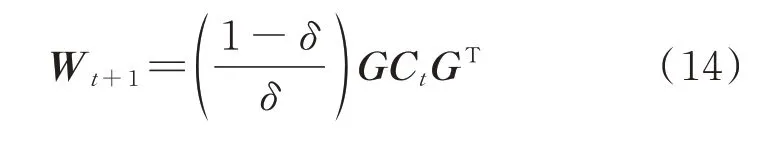
式中δ为折扣因子,取值范围为0.95~0.98。折扣因子δ对预测精度影响很大,选择合适的δ能够使贝叶斯动态线性模型的预测精度快速收敛[15]。状态变量以及状态一阶差分量的方差矩阵Ct可表示为:
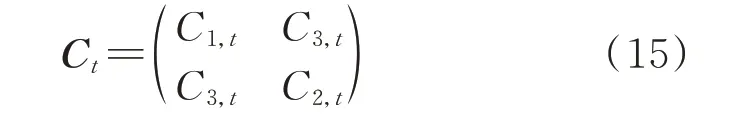
其中,方差矩阵中对角元素C1,t,C2,t可分别通过计算初始状态数据以及初始状态一阶差分数据的方差获得。θi,t与βi,t的协方差C3,t可由下式近似得到:
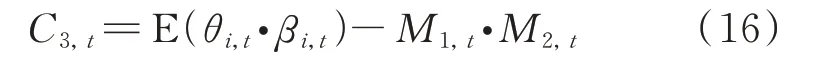
式中M2,t为初始状态数据一阶差分结果的期望值,可由数据的均值近似得到。
利用监测数据以及状态变量θi,t+1,可得到单分量极值应力的Hilbert 动态线性模型中的监测方程。假设监测值与状态变量呈线性关系,并考虑监测误差的影响,监测方程可表示为:
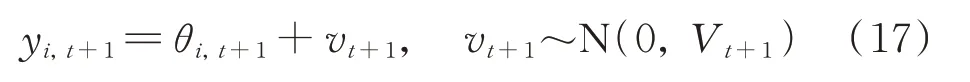
式中yi,t+1为t+1 时刻单分量极值应力监测值;vt+1为监测误差并假设监测误差服从期望为0,方差为Vt+1的正态分布。根据公式(17)可知,对单分量极值应力yi,t与状态数据θi,t之间的差值进行统计分析,可近似得到监测误差的方差Vt+1。
结合公式(11),(15)和(16),t时刻以及t时刻之前初始状态信息的后验概率分布可整理为:
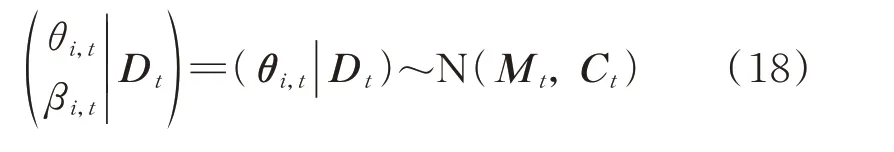
式中θi,t为状态变量向量;为状态变量和状态一阶差分量的期望向量;Dt表示t以及t时刻之前监测数据的信息集合,包括t时刻的监测数值yi,t,t-1 以及t-1 时刻之前的Mt-1和Ct-1。
3 HDLM 的贝叶斯概率递推
在建立单分量极值应力的HDLM 之后,结合贝叶斯方法可得到BHDLM。根据t时刻状态变量θi,t的后验分布可对t+1 时刻的极值应力yi,t+1进行预测。再利用贝叶斯方法以及实际监测数据对模型中t+1 时刻的状态变量后验分布θi,t+1概率进行修正,使得下一时刻的预测结果更加合理。这样,随着模型中的参数不断更新,BHDLM 即可实现对单分量极值应力的动态预测并且精度不断提高。模型的概率递推过程如图2所示。

图2 BHDLM 的概率递推过程Fig.2 The probability recursive process of BHDLM
BHDLM 递推过程中参数更新如下所示[19-22,27]:
(1)t+1 时刻的状态变量先验概率密度分布
结合公式(18)给出了状态变量θi,t在t时刻的后验概率密度分布。根据状态方程可得到t+1 时刻的θi,t+1和βi,t+1先验概率密度分布,表示为:
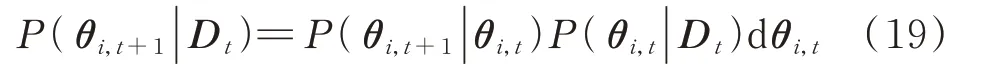
简化可得:

式中
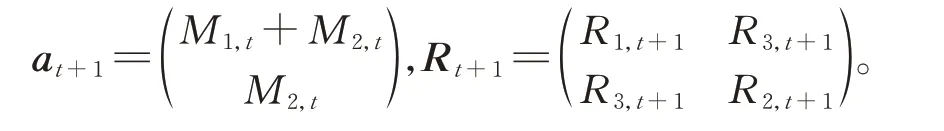
其中,R1,t+1=C1,t+2C3,t+C2,t+W1,t+1,R2,t+1=C2,t+W2,t+1,R3,t+1=C3,t+C2,t+W3,t+1。
(2)t+1 时刻监测变量的一步向前预测概率密度分布P(yi,t+1|Dt)
结合状态变量的先验概率P(θi,t+1|Dt)以及监测方程,即可得到监测变量一步向前预测概率密度:
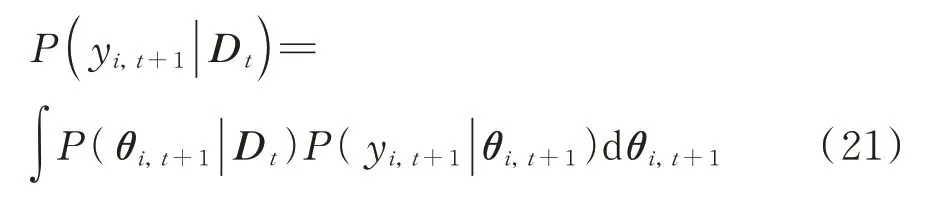
简化可得监测变量概率密度:
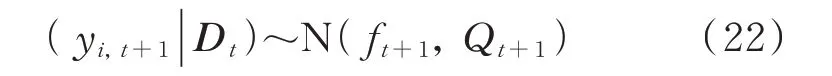
式中 预测值ft+1=at+1(1,1);预测方差Qt+1=Rt+1(1,1)+Vt+1。而预测方差的倒数则为BHDLM的预测精度[21]。
(3)t+1 时刻的状态变量后验概率
密度分布P(θt+1|Dt+1)
当已知t+1 时刻的监测值Yt+1后,结合公式(20)和(22)以及贝叶斯方法,t+1 时刻的状态变量θt+1后验概率密度分布可表示为:
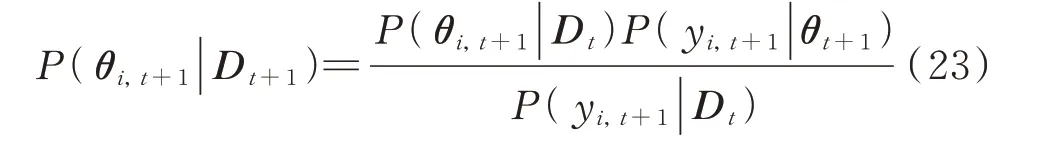
简化可得:
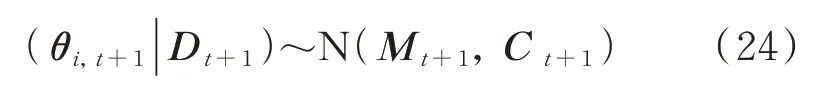
式中 期望向量Mt+1中M1,t+1=at+1(1,1)+A1,t+1·et+1,M2,t+1=at+1(1,2)+A2,t+1·et+1,其中,适应性系数A1,t+1=Rt+1(1,1)/Qt+1,A2,t+1=Rt+1(1,2)/Qt+1,一步预测误差et+1=yi,t+1-ft+1;方差矩阵Ct+1中C1,t+1=A1,t+1·Vt+1,C2,t+1=Rt+1(2,2)-A2,t+1·Rt+1(1,2),C3,t+1=A2,t+1·Vt+1。
4 实桥分析
派河大桥主桥上部结构为飞燕式钢箱拱桥,跨径组合为54 m+130 m+54 m。拱圈和钢梁采用Q345D 钢材,弹性模量为206 GPa。为了全面监测桥梁在运营期间的极值应力应变,全桥共选取5 个关键截面布置了32 个应变传感器,应变监测截面布置图如图3所示。其中,钢纵梁的应变传感器安装在钢纵梁内部,每个截面安装4 个传感器。为了了解拱脚处钢纵梁的应力状态,定义每小时监测最大应力为桥梁耦合极值应力Yt,并提取了12#墩附近2-2 截面Sx9~Sx12 监测点一年(共8571 h)的历史监测数据。其中,2-2 截面钢纵梁应力监测点布置如图4所示。
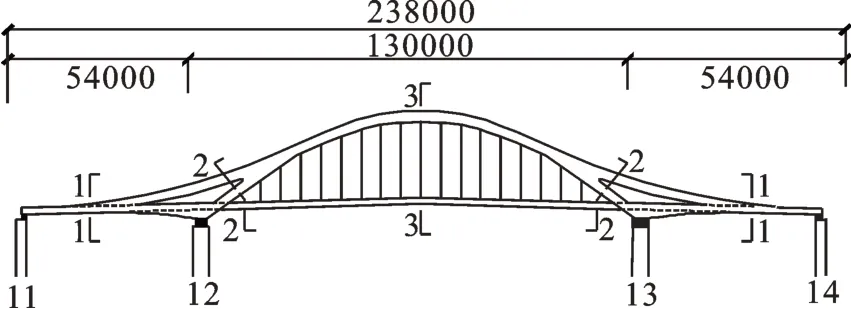
图3 应力监测截面布置图(单位:mm)Fig.3 The layout diagram of stress monitored section(Unit:mm)
4.1 基于BHDLM 的桥梁耦合极值应力分析
为了验证本文所提方法的有效性,现选取Sx12测点历史监测数据中前3000 h 作为建模数据,建立各阶单分量极值应力的HDLM。再利用建立的模型以及贝叶斯方法,对剩余5572 h 的极值应力进行动态预测。其中,Sx12 测点采集的历史监测数据如图5所示。
对建模数据进行傅里叶变换,结果如图6所示。从图6 中可以看出,历史监测数据是多模态响应耦合的数据。
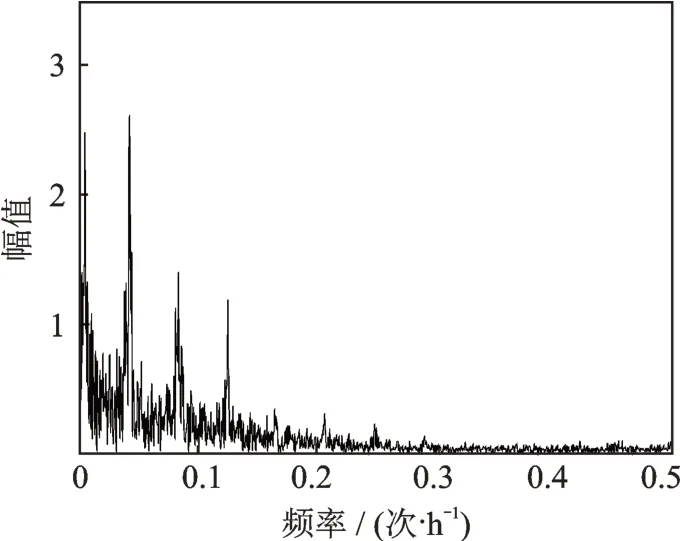
图6 Sx12 测点极值应力数据的傅里叶谱图Fig.6 The Fourier spectrum of the extreme stress data of the Sx12 measure point
结合傅里叶分析结果和Hilbert 信号分解算法对前3000 h 耦合极值应力进行解耦,可得到4 个具有单一频率的单分量成分yi,t(i=1,2,3,4)。基于公式(3)~(9),分别对yi,t进行解调,即可得到单分量极值应力的状态数据回归函数θi,t(i=1,2,3,4)。解调结果为:
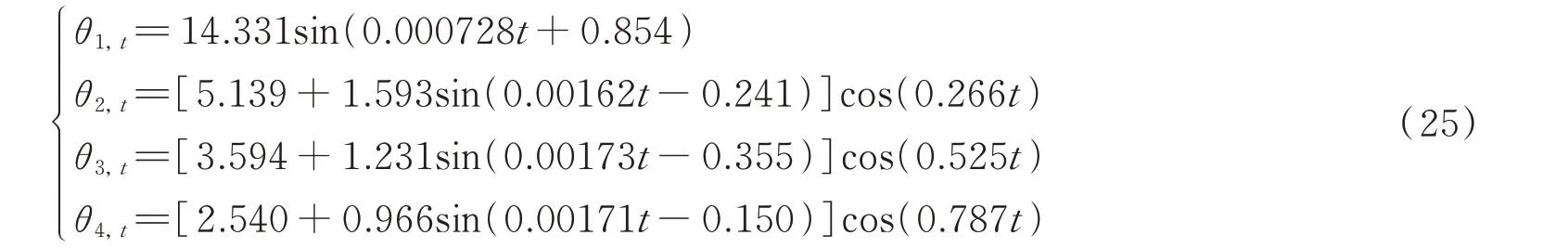
首先,基于y1,t以及θ1,t,对桥梁耦合极值应力中的一阶单分量应力数据进行预测。根据θ1,t的回归公式可得θ1,t+1:
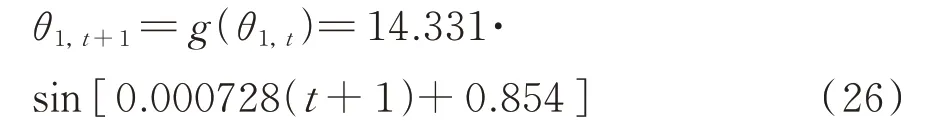
则基于公式(25),(26)和(12)可知,θ1,t≈θ1,t+1,即可认为θ1,t+1仅和前一时刻的θ1,t有关,与状态数据的 一 阶 差 分 变 量β1,t无 关,且G1=。其中,监测应力和初始状态信息如图7所示。
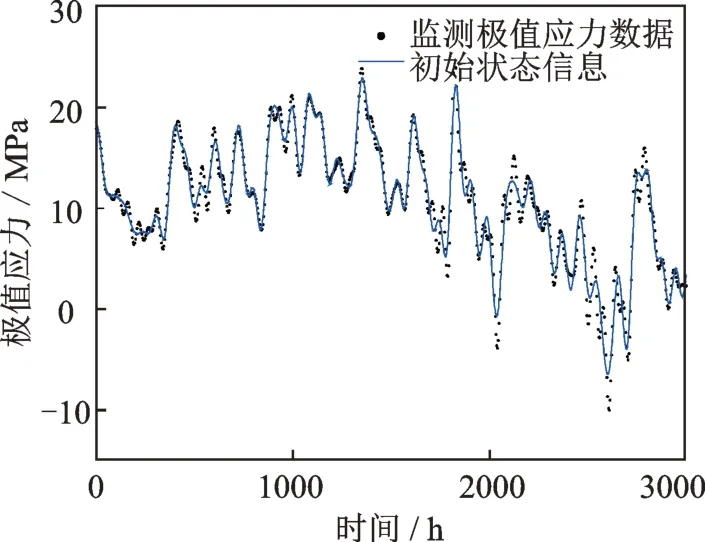
图7 第一阶解耦应力数据以及初始状态信息Fig.7 The first order decoupled stress data and initial state information
则初始状态信息为:

则根据公式(13),状态方程可简化为:
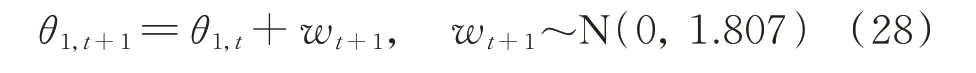
其中,折扣因子δ的取值为0.95。监测方程为:

在得到0~2999 h 监测数据的动态线性模型后,结合公式(19)~(24),可对3000~8573 h 的数据进行动态预测,一步预测结果以及预测精度分别如图8 和9所示。从图8 的预测结果中可以看出,第一阶单分量极值应力的预测值与监测数据近似相等,证明本文所提模型预测效果较好。而结合图9 的预测精度结果可以看出,预测应力区间可以包含所有的监测应力数据,随着单分量极值应力数据的远程更新,精度越来越高并最终趋于稳定,说明本文所提模型的合理性。

图8 第一阶解耦极值应力数据预测结果Fig.8 The predicted results of the first order decoupled extreme stress data
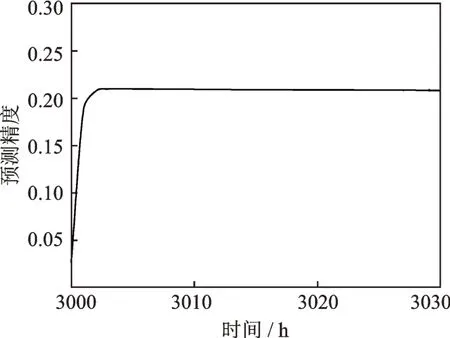
图9 BHDLM 的预测精度Fig.9 The prediction precision of BHDLM
同样的,基于y2,t以及θ2,t,对桥梁耦合极值应力中的二阶单分量应力数据进行预测。根据θ2,t的回归公式可得θ2,t+1:
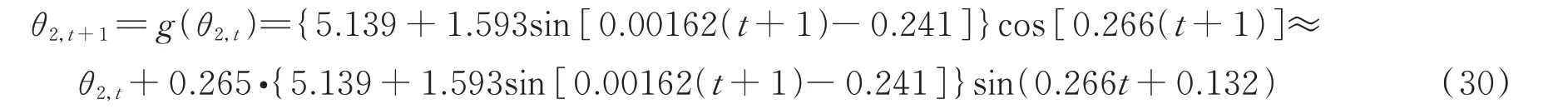
基于公式(25),(30)和(12)可知,监测方程中θ2,t+1与前一时刻的θ2,t和状态数据的一阶差分变量β2,t有关。利用差分计算可得状态变量转移矩阵中其中,监测应力和初始状态信息如图10所示,初始状态信息的一阶差分值如图11所示。
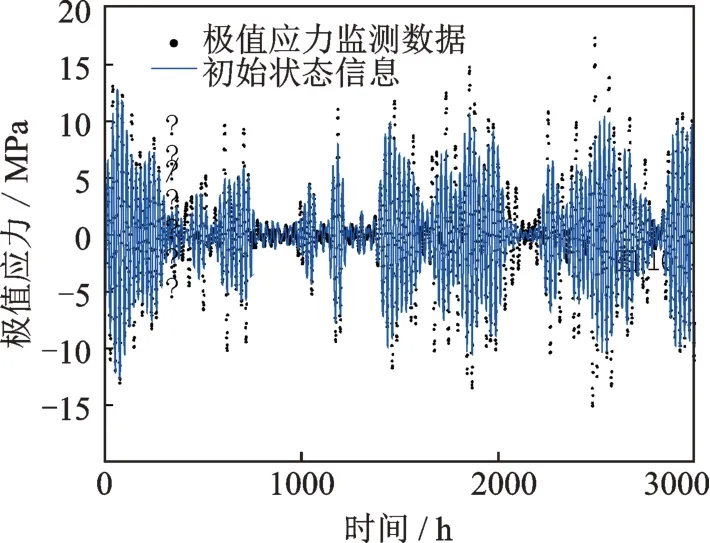
图10 第二阶解耦应力数据以及初始状态信息Fig.10 The second order decoupled stress data and initial state information
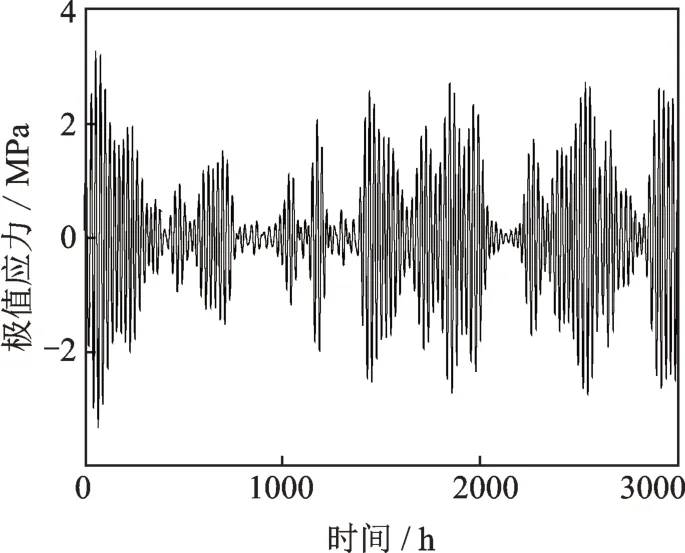
图11 初始状态信息的一阶差分值Fig.11 The first order differential data of initial state information
则根据图10 和11,初始状态信息可表示为:
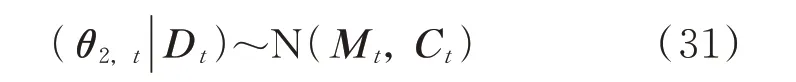
其中
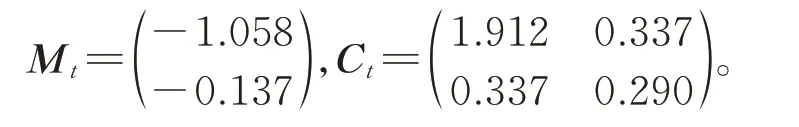
而根据公式(13),状态方程为:
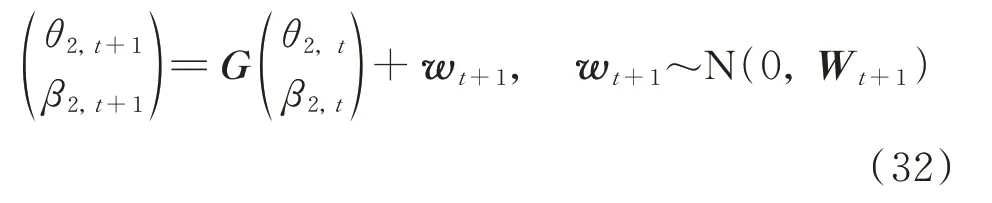
其中,折扣因子δ的取值范围为 0.95,。
监测方程为:
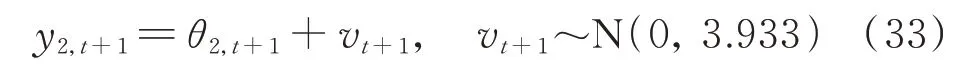
利用贝叶斯方法,对3000~8572 h 的数据进行动态预测,预测结果如图12所示,预测值与监测值接近,预测效果较好。预测精度如图13所示,随着数据的更新,预测精度趋于稳定。
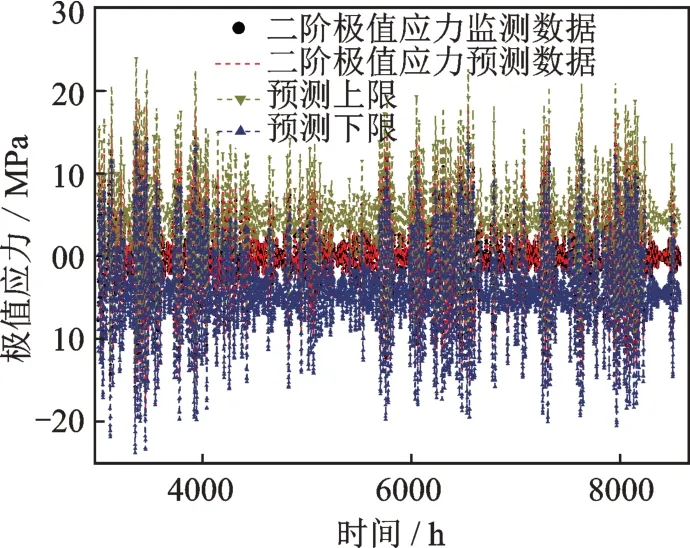
图12 第二阶解耦极值应力数据预测结果Fig.12 The predicted results of the second order decoupled extreme stress data

图13 BHDLM 的预测精度Fig.13 The prediction precision of BHDLM
将第3和4阶单分量极值应力数据按上述步骤进行动态预测,则桥梁耦合极值应力即为各阶单分量极值应力动态预测值相加,预测结果如图14所示。
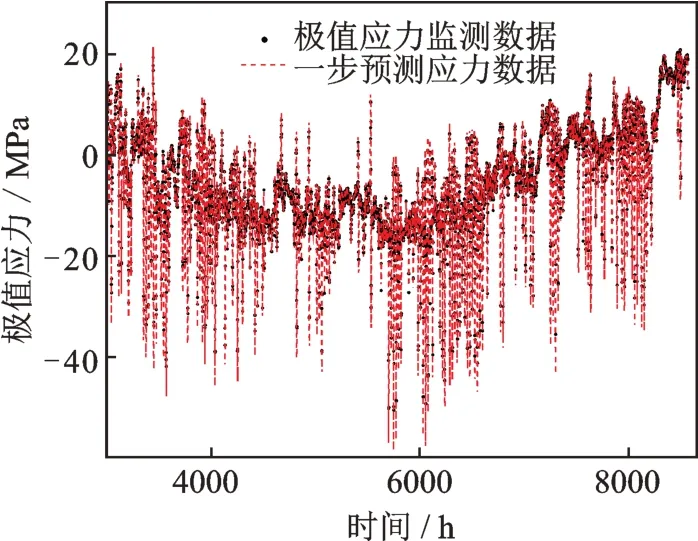
图14 Sx12 测点桥梁耦合极值应力预测结果Fig.14 The predicted results of bridge coupled extreme stress of the Sx12 measure point
按照上述流程,利用BHDLM 可进一步得到Sx9,Sx10 和Sx11 这3 个测点3000 h 以后的桥梁耦合极值应力动态预测结果,预测结果如图15~17所示。可以看出,耦合后的极值应力动态预测值与实际监测值接近,说明了本文所提方法能够较好地预测桥梁耦合极值应力。
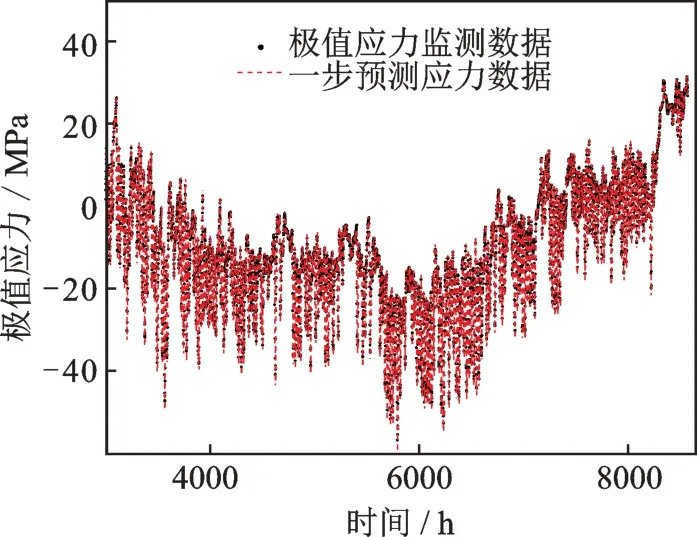
图15 Sx9 测点桥梁耦合极值应力预测结果Fig.15 The predicted results of bridge coupled extreme stress of the Sx9 measure point
4.2 耦合极值应力预测准确度对比分析
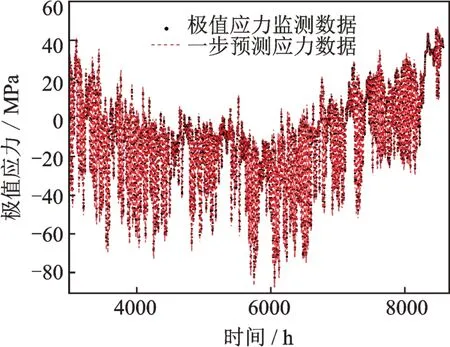
图16 Sx10 测点桥梁耦合极值应力预测结果Fig.16 The predicted results of bridge coupled extreme stress of the Sx10 measure point
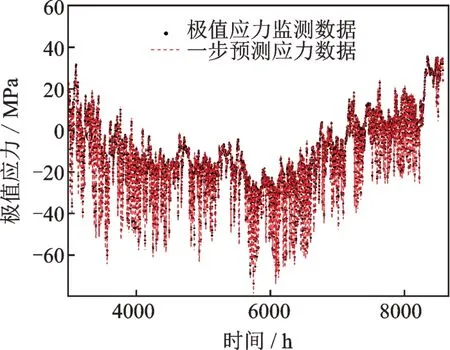
图17 Sx11 测点桥梁耦合极值应力预测结果Fig.17 The predicted results of bridge coupled extreme stress of the Sx11 measure point
为了验证BHDLM 的在预测桥梁耦合极值应力方面的优越性,本文利用贝叶斯动态线性模型(Bayesian Dynamic Linear Model,BDLM)对Sx12测点处的极值应力进行了动态预测。同时,采用均方根误差(Root Mean Squared Error,RMSE)作为模型预测准确度指标,用于模型预测准确度的比较分析。其中,预测准确度指标RMSE可表示为:
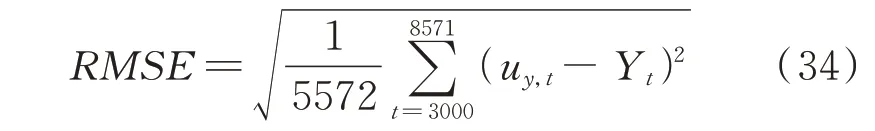
式中uy,t为桥梁耦合极值应力预测值;Yt为桥梁耦合极值应力监测值。
BDLM 预测结果如图18所示。根据图18 的预测结果并结合公式(34),可得BDLM 预测准确度指标RMSE为2.59。而利用本文提出的BHDLM 进行动态预测时,模型预测准确度指标RMSE则为1.60。证明了本文所提方法相比于BDLM 具有更高的预测准确度,更具优越性。
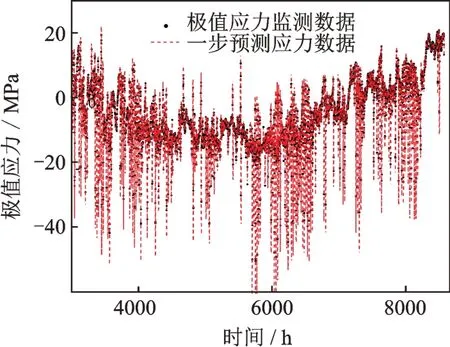
图18 利用BDLM 得到的桥梁耦合极值应力预测结果Fig.18 The predicted results of bridge coupled extreme stress by using BDLM
5 结论
桥梁耦合极值应力可视为有限多个单分量极值应力的累加。在考虑到单分量极值应力周期性、随机性等数据特点的情况下,提出了单分量极值应力的BHDLM。通过对单分量极值应力的动态预测,进而可得到桥梁耦合极值应力的预测结果。最后,利用派河大桥一年的实际监测数据进行分析验证,得到如下结论:
(1)通过Hilbert 信号分解及解调技术可对桥梁耦合极值应力数据进行解耦,并建立各阶单分量极值应力数据的HDLM。
(2)基于解耦得到的单分量极值应力数据以及BHDLM,可对单分量极值应力进行合理预测,预测精度随着模型参数的更新不断提升。
(3)桥梁耦合极值应力的最终预测结果与监测数据基本一致,具有较好的预测准确度。验证了本文提出方法在实际工程中的可行性与有效性。
