某露天矿高边坡稳定敏感性因子分析
2022-07-26周琪,钟兴
周 琪,钟 兴
(湖南元天检测技术有限公司,湖南长沙 410007)
0 引言
目前,我国露天矿存在许多安全问题,主要体现在边坡的稳定性[1]方面,而影响边坡稳定性的因子很多,且各个因子之间有着复杂及不确定的因素。当前对其进行分析评价的方法主要是从地形地貌、地质特性、地下水、地震等[2]。在一定的边坡工程地质条件下,就边坡稳定性而言,有些因素对其影响大,有些因素对其影响小,这就是说,影响边坡稳定性的因素其贡献度不同[3]。影响边坡稳定因子的敏感性分析是定量地分析,并找出边坡安全系数与边坡稳定各影响因素之间的一一相关性。在矿区边坡设计及开采边坡治理工程中进行敏感性分析,不但能够直观的发现边坡失稳的主要因素,而且对治理边坡失稳及优化设计露采边坡都具有重要意义[4]。通过敏感性分析找到边坡失稳的主要影响因子,在设计方面能更好的把握优化对象,且能有针对性地治理边坡。
1 边坡稳定敏感性分析的计算方法
1.1 边坡稳定性计算公式
边坡稳定性计算是指根据露天矿的实际条件,计算露天矿边坡所需保持一定稳定系数的边坡角。目前边坡稳定性计算主要还是采用二维断面进行进行分析,其稳定性分析方法主要有3 种:①刚体极限平衡法[5],把滑体看作刚体,滑动面的形成是剪切破坏造成的,其边坡稳定系数是通过块体在斜坡上得平衡原理而确定的。②数值分析法[6],其中包括有离散单元法、边界单元法、有限单元分析法等其他方法,通过数值计算得出的边坡体内部的位移和应力分布来确定边坡稳定性。③概率分析法[7],通过数理统计方法分析得到的边坡稳定性系数。
边坡稳定性分析方法最常用的为刚体极限平衡分析法,其计算力学模型如图1 所示。

图1 边坡稳定性计算力学模型
其安全系数的确定可按式(1)计算。

式中:Wi——第i 条块土重,Wi=γHiBi;Ui——第i 条块底面水压力,Ui=hwiγwli;γ——土体重度;γw——水的重度;Hi——第i 条块的高;hwi——第i 条块底面的水头;bi——第i 条块的宽;li——第i 条块底面的底边;li——第i 条块底面的底边;βi——第i 条块底面倾角;c——滑带土的粘聚力;φ——滑带土的内摩擦角。
根据式(1)不难发现,在边坡坡率、坡高已定的情况下,安全系数Fs的影响因素有滑体容重γ、滑体地下水位hw、滑带土黏聚力c 和内摩擦角φ 等[8]。影响边坡安全系数Fs中各个因素的作用不同(即敏感性大小不同),所以需要通过定量的标准来找到较大的影响因子,把该因子作为重点研究的对象来治理滑坡或滑坡加固设计,对边坡整治产生较好的效果。
1.2 敏感性分析计算方法
通过对边坡稳定有影响的各因子与边坡稳定系数的对应关系,该关系是通过边坡稳定系数的相对变化率与各影响因子之间的相对变化率之间的比值来确定的[9]。
各影响因素的变化会导致边坡的稳定系数的变化(即为函数关系),假定边坡的稳定系数为Fs,可得式(2)。

则敏感度Si可按式(3)计算。

徐宏等[10]研究了安全系数的敏感性大小与边坡各影响因素之间的关系,Fs对γ、hw、c、φ 求偏导数,求出各影响因子对安全系数Fs的偏导数,比较不同γ、hw、c、φ值下各偏导数的值,以此确定敏感度Si值,通过敏感度Si值的大小分析出各影响因素对滑坡的影响,由此指导边坡的防治。
2 边坡稳定敏感性分析实例
2.1 工程地质概况
2.1.1 地理位置与地形地貌概况
本文以某铜钴矿区高边坡[11]为例。该矿区面积约为10.91km2,矿区到主干公路约15km,路况较好,交通比较便利,总体地势为东南高、西北低,海拔标高1375~1525m,地貌类型为低缓丘陵。
2.1.2 区域工程地质条件
(1)地层岩性和地质构造
本区域分布的地层主要为加丹加系和第四系,加丹加岩系主要为恩古巴群(Ng)、罗安群(R)、孔德龙古群(Ku)。该区域主构造线为北东30°~40°,主要构造为褶皱构造、断裂构造及不整合接触构造等。
(2)水文地质特征
工作区地处赤道南侧,属于热带干湿季气候。工作区处于赤道低压带与信风带交替控制区。一年之中有明显的干季和湿季,区内湿季为每年的5—10 月,干季为11 月至次年4 月。区内年平均气温20℃。在干季相对湿度为83%,旱季相对湿度为40%。区内东北、东南风为主导风向,平均风速11m/s,最大风速20m/s。
该矿区位于吕卢河汇水盆地中,区域研究范围自东、西、南三面地表分水岭至东北部吕卢镇一带,面积250km2。吕卢河控制着区内地下水流动系统。地下水接受大气降水入渗补给后,依地势从分水岭向沟谷汇聚,溢出成泉或形成湿地,汇流到吕卢河各支流,构成吕卢河基流量,根据勘探期间吕卢河流量过程曲线分析,吕卢河基流量0.77~2.62m3/s,平均1.53m3/s。
2.1.3 岩土体参数指标
通过室内土工试验,与当地的经验值确定岩土体的参数指标,并与Hoek-Brown 准则相比较综合得出如表1 所示的岩土体参数指标。
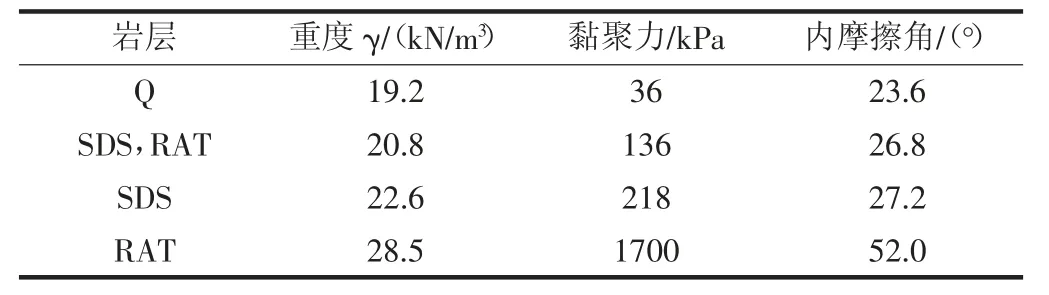
表1 最终岩体的力学参数
2.2 参数的敏感性分析
由于地形情况比较复杂,在进行边坡的稳定性分析中,内摩擦角,黏聚力,地下水,岩土体的容重都是进行分析的重要参数,每一个因素的变化都可能导致边坡的稳定性发生很大的变化,现在将以本边坡为例研究上述因子对边坡的敏感程度。
2.2.1 内摩擦角敏感性分析
下文通过岩土体不同的内摩擦角所引起的边坡安全系数的变化分析两者之间的敏感度,得出安全系数Fs与岩土体内摩擦角φ 的关系式,如式(4)、式(5)所示。

从式(4)、式(5)可以看出,安全系数对岩体内摩擦角的敏感程度比对土体内摩擦角敏感程度大,其中对于土体来说安全系数随着内摩擦角的增大变化很小,变化率平均值为0.0004/度,敏感度S 值为0.04;对于岩体来说安全系数随着内摩擦角的增大而线性增大,变化率平均值为0.0227/度,敏感度S 为0.552。
2.2.2 地下水水位敏感性分析
下文通过地下水水位变化引起的安全系数的变化分析敏感度。得出安全系数Fs与地下水水头hw之间关系,如式(6)所示

边坡上部边界水头1300m,坑底水头1003m,浸润线高水位点距坡顶的距离为地下水位的高度,坡顶为0,向下依次增大。由于采用单因子敏感性分析,没有考虑地下水对岩土体物理力学指标的影响。因此,只能总体反映地下水对边坡的敏感度,不能比较地下水对土质边坡和岩质边坡的敏感程度。从式(6)不难得出,安全系数对地下水较敏感,随着地下水位降低而增大,变化率平均值为0.0016/m,敏感度S 为0.132。
2.2.3 容重敏感性分析
下文通过土体和岩土的不同容重所引起的安全系数的变化分析两者之间的敏感度。得出安全系数Fs与岩土体重度γ 之间关系,如式(7)、式(8)所示。

从式(7)和式(8)可以得出,伴随着岩土体容重的增大边坡的安全系数逐渐减小敏感性比较明显,对边坡的稳定性都起着消弱的作用。对本边坡来说,土体Fs-γ关系为反向陡倾直线,变化率平均值为-0.0083/kN·m-3,敏感度S 为0.122;岩体Fs-γ 关系为缓倾直线,变化率平均值率为-0.0032/kN·m-3,敏感度S 为0.049。说明土体边坡比岩土边坡在重度方面更敏感。
2.2.4 黏聚力敏感性分析
下文通过土体和岩土的不同黏聚力所引起的安全系数的变化分析两者之间的敏感度。得出安全系数Fs与岩土体黏聚力c 之间关系,如式(9)、式(10)所示。

从式(9)和式(10)可以看出,伴随着岩土体黏聚力不断增大边坡的安全系数也逐渐增强。对本边坡来说,其中岩体Fs-c 关系正向陡直线,安全系数对粘聚力的变化率为0.0008/kPa,敏感度S 为0.222。土体Fs-c 关系为正向倾斜直线,变化率为0.0003/kPa,敏感度S 为0.007;因此可以得出岩体的黏聚力对边坡安全系数的敏感程度比土体强。
3 总结
从表2 可以得出如下的结论。

表2 影响因子敏感度及其作用下的边坡安全系数变化率
(1)从纵向看来容重对边坡的安全系数起着反向作用,即随着容重的增大,安全系数有逐渐降低的趋势。内摩擦角和黏聚力起着正向作用,提高岩土体的内摩擦角和黏聚力由于提高边坡的安全性系数。
(2)土体和岩土分开进行比较来看,不同介质属性各个因子产生较大的差别,比如:对于内摩擦角岩体的敏感程度比土体的敏感度要大很多,另外岩体粘聚力的敏感性也大于土体的。但是对于容重来说土体的敏感度大于岩体的。
(3)地下水位的深度与边坡的稳定性反向的相关关系,水位越高,边坡的安全性越低。
4 结语
通过边坡稳定敏感性分析,发现在治理高边坡滑坡工作中,除了采用常规方法去有效的降低坡高和放缓边坡坡度外,还应该提高与安全系数正相关的参数如c、φ 值和降低地下水位hw,对以后在此类似的露天矿高边坡治理方面有一定指导价值。
