Gamma ray multiplicity of a 240Pu solid sphere simulated by JMCT
2022-07-26HuanHuanDingFanGaoChangBingLuRuiLiChenGuangLiZhaoHongMoDunFuShiMingSuDeShanZhaoMaoBingShuaiZhongHuaXiongBinYuanXiaYunBai
Huan-Huan Ding · Fan Gao · Chang-Bing Lu· Rui Li · Chen-Guang Li·Zhao-Hong Mo · Dun-Fu Shi · Ming Su · De-Shan Zhao · Mao-Bing Shuai ·Zhong-Hua Xiong · Bin-Yuan Xia · Yun Bai
Abstract Determining the mass of plutonium metal is an important research objective in the field of nuclear material accounting and control. Based on the 3D neutron and photon transport code JMCT (Jointed Monte Carlo Transport),the gamma ray multiplicity of 240Pu was simulated in this study, and the average number of gamma rays leaking from 240Pu solid spheres with different masses was also obtained. The simulation results show that there is a oneto-one correspondence between the average number of gamma rays and the mass of 240Pu solid spheres in the range of 0.50–3.00 kg. This result provides a basis for using the average number of gamma rays to account for the mass of 240Pu.
Keywords 240Pu·JMCT·Gamma ray multiplicity·Solid sphere mass · Surface-to-volume ratio
1 Introduction
When a nucleus undergoes fission, the primary fission fragments are always formed in a state of high excitation and de-excite through the evaporation of prompt neutrons and emission of prompt gamma rays. The statistical properties of the numerical distribution of neutrons and gamma rays generated in fissile samples are important and have been studied using experimental data, analytical methods,and Monte Carlo simulations. It is well known that the number of neutrons evaporated in spontaneous fission can vary from 0 to 6 or more [1], whereas the prompt gamma rays can range from 0 to 20 per fission by fitting the measured experimental data [2]. The emission of prompt neutrons has been used as a means to determine the mass of fissile materials; however, there is little published work regarding the gamma-ray multiplicity distributions of fission systems. For gamma-ray multiplicity, most studies focus on general properties, such as the average energy dissipated,average multiplicity,or peak multiplicity[3–6].Other works have studied the competition in the emission of prompt gamma rays and neutrons from the de-excitation of fission fragments by considering quantum mechanical selection rules for the conservation of angular momentum[7].
In recent decades, extensions of non-destructive assay measurements using detectors sensitive to both neutrons and gamma rays have been proposed [8]. To use gamma ray multiplicity data to determine the fissile mass, some experiments have been performed using scintillation detectors to measure the properties of prompt gamma rays for thermal-neutron-induced fission of235U [9] and239Pu[10], and spontaneous fission of252Cf [11]. The results show that the average number of gamma rays emitted per fission for the three nuclides is 6.51±0.3,6.88±0.35,and 8.32±0.4,respectively.Based on these data,Valentine[8]estimated the prompt gamma ray multiplicity parameters for some spontaneous fission nuclei, such as238U,238Pu,240Pu,242Pu,242Cm, and244Cm, which provides an approximate method using the correlation of neutron and gamma emissions in fission to estimate the average number of gamma rays from the fission process [8].
At present, in addition to determining the sample mass by neutron multiplicity counting, gamma-ray multiplicity has also been considered. There are several reasons for using gamma multiplicity counting, including higher gamma ray multiplicity per fission, greater ability to penetrate through most strong neutron absorbers,and relatively easy detection by organic scintillation detectors. Based on this concept,gamma-ray multiplicity has been suggested as a potential method for nuclear safeguards [12, 13]. P′azsit et al.[14]studied the first three moments of the gamma-ray multiplicity distribution (i.e., singlet, doublet, and triplet rates). As shown in ref [14],because the values of the first three moments for gamma ray multiplicity increase faster with an increase in the fission probability than those for neutron multiplicity, gamma ray multiplicity is a more sensitive method for estimating the sample mass and multiplication. Enqvist et al. [15] derived the neutrongamma joint distribution; however, the mixed moments of the joint distribution were highly nonlinear. To solve this problem, they used an artificial neural network [15] to determine the sample parameters, especially the fission rate,which is closely linked to the sample mass.According to this result, artificial neural networks can also be used as a replacement for pure neutron assay without loss of accuracy compared to the conventional unfolding of three sample parameters.
Currently,software has been developed to study neutron and gamma ray multiplicities. The MCNP-PoliMi code, a modified version of the standard MCNP code [16], was used to calculate neutron and gamma ray multiplicities,and good agreement was found between the quantitative results and the Monte Carlo results [14, 17, 18]. The fission reaction event yield algorithm (FREYA) [19, 20] was designed to generate fission events and provide specific correlations for prompt neutrons, gamma rays, and fragments. FREYA was employed to estimate the fission spectrum of the sequential neutron emission following neutron-induced fission of240Pu,and the uncertainties were several times smaller than those of the current experiment for outgoing neutron energies of less than 2 MeV [21].FREYA has also been integrated into the particle transport code MCNP5 as a private modification to study the neutron multiplication distribution and angle correlation of240Pu spontaneous fission (sf) [22]. This approach allows for more accurate modeling and is able to simulate correlations that are not predicted by conventional neutron Monte Carlo codes.
Furthermore, the 3D neutron and photon transport code JMCT(Jointed Monte Carlo Transport)[23]was developed based on the framework of JCOGIN [24]. JMCT can use both multi-group and pointwise continuous energy cross section data obtained from the evaluated nuclear data file ENDF/B-VII.0. Furthermore, JMCT can calculate the multiplicities and correlation of the neutrons and photons of the nuclear fission process.In this study,the gamma ray multiplicity distribution of240Pu was investigated, and the average number of gamma rays leaking from240Pu in the form of a solid sphere, solid cube, and solid rectangular parallelepiped with different masses was also calculated using JMCT.The relationship between the average number of gamma rays leaking from the240Pu solid spheres and their masses was obtained.
2 JMCT modeling
2.1 Prompt gamma ray multiplicity of 240Pu
JMCT provides the ability to calculate the gamma ray multiplicity for many nuclides of plutonium, such as spontaneous fission nuclides238Pu,240Pu,242Pu, and neutron-induced fission nuclides239Pu,241Pu. However, for plutonium metals produced in the real world (especially in the process of the nuclear fuel cycle), the yields of238Pu,241Pu, and242Pu are the lowest, while the yield of239Pu is the highest, followed by240Pu. The spontaneous fission probability is small for239Pu and relatively high for240Pu;thus, the spontaneous fission yield of239Pu is smaller than that of the same mass of240Pu.Furthermore,for plutonium metals with different compositions of239Pu and240Pu, the total quantity of gamma rays produced by fission (including spontaneous and induced fission) varies depending on the mass of the sample. The composition of plutonium metals in the real world is variable; to simplify the complexity of the following calculations,240Pu is selected for the calculation of gamma ray multiplicity and the relationship between the average number of gamma rays and the sample mass, because of its higher probability of spontaneous fission. The average gamma ray multiplicity for all types of plutonium compositions can be calculated using JMCT.
During the simulation, the gamma ray multiplicity distribution of a point240Pu source was calculated based on ENDF/B-VII.0 using JMCT. The Watt fission parameters for240Pu (sf) and the neutron-gamma coupled transport were also applied in this calculation. The total number of gamma rays per fission was determined. To reduce the calculation time cost, an energy cutoff of 0.05 MeV was applied. This value was chosen because it has very little effect on the calculation result, but it greatly reduces the calculation time. The number of fission particles in the simulation is 1.0×107. The gamma-ray multiplicity distribution of240Pu is shown in Fig. 1.
From Fig. 1, the average number of gamma rays for240Pu (sf) is 6.49 ± 0.02, where 0.02 is the standard deviation of the average number of gamma rays in the simulation. For comparison, Table 1 shows the average number of gamma rays for240Pu(sf)obtained in this study with the corresponding results from the estimated average number of gamma rays reported by Valentine [8] and the result of the first prompt fission experiment for the average multiplicity for240Pu (sf) [25].
The fission events and neutron-gamma transport are calculated by JMCT with the multi-group energy crosssection data, and the energy-related parameters in JMCT are converted to the average value in the energy group.Thus, the average number of gamma rays obtained in this work as shown in Table 1 agrees with the estimated average number of gamma rays reported by Valentine [8]within error permissibility. However, the first prompt fission experiment result for the average multiplicity (8.2 ±0.4) for240Pu [25] is much greater than the estimatedaverage number of gamma rays and our result. For the240Pu experiment average multiplicity, a greater result is drawn from a limited number of events and may show a possible correlation of prompt gamma-ray emission with the distinct shape of the fission fragment distribution [25].As observed by Oberstedt et al. [25], to fully understand the underlying physics of this experimental result, more data are needed. Therefore, the calculations in this study are carried out in accordance with Valentine [8]; further,confirmed experimental data can be used in future simulations to calculate the gamma ray multiplicity of240Pu and to understand its physics.

Table 1 Average number of gamma rays for 240Pu (sf) from this study compared with the estimated average number of gamma rays reported by Valentine [8] and the result of the first prompt fission experiment for the average multiplicity for 240Pu (sf) [25]

Fig. 1 (Color online) Prompt gamma ray multiplicity distribution of 240Pu, as simulated by JMCT
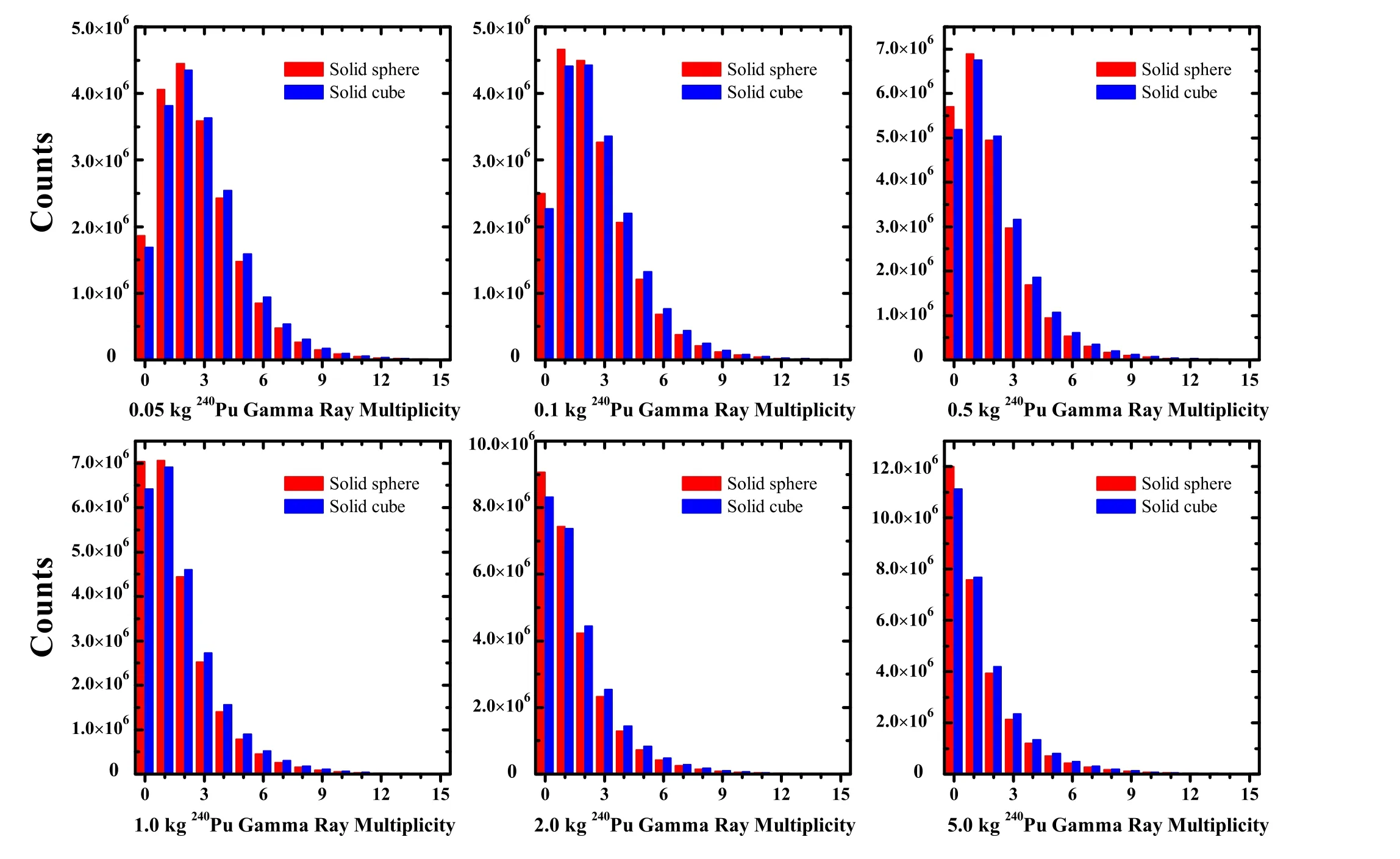
Fig. 2 (Color online) Gamma ray multiplicity distribution for 240Pu solid spheres and solid cubes with different mass
2.2 Average number of gamma rays for 240Pu solid spheres and solid cubes
To obtain the relationship between the average number of gamma rays and the sample mass for240Pu, the gamma ray multiplicity was simulated for240Pu solid spheres with different masses; for comparison, the gamma ray multiplicity for240Pu solid cubes with equal mass was also simulated.
The simulations were performed for nine solid spheres of240Pu with masses of 0.05, 0.10, 0.20, 0.50, 1.00, 2.00,3.00,4.00,and 5.00 kg,and nine240Pu solid cubes of equal masses. The simulation conditions (the Watt fission parameters, neutron-gamma coupled transport, energy cutoff,and ENDF/B-VII.0 database)are the same as above.More importantly, a uniform sampling of the positions within the geometry for the nine240Pu solid spheres and cubes was used in the simulation.To perform the transport of gamma rays, the photoelectric effect, pair production,and Compton scattering were considered in JMCT. Moreover, on the basis of the above three interactions, coherent scattering and the cross section for Compton scattering modified by the form factor that deal with high Z material and deep penetration problems of the gamma rays have also been added in JMCT.The total number of gamma rays leaking out of the240Pu surface was counted. Figure 2 shows the calculated gamma ray multiplicity for the240Pu solid spheres and an equal mass of240Pu solid cubes. The average number of gamma rays and their standard deviation for each240Pu solid sphere and solid cube are given in Table 2, as well as their ratio (R).
As shown in Fig. 2, because of the interactions of gamma rays with the240Pu considered in JMCT,the single,double (and zero) counts in the gamma ray multiplicity distribution increase with an increase in the240Pu mass,which is quite different from that in Fig. 1.Meanwhile,the average numbers of gamma rays for the nine240Pu solid spheres and cubes listed in Table 2 decrease gradually with increasing mass.The average number of gamma rays for a240Pu solid cube is larger than that for a solid sphere with equal mass,and their ratio(R)is always larger than 1.00,in the range of 0.05–5.00 kg.
The most obvious feature is that the average number of gamma rays leaking from the240Pu solid spheres and cubes decreases with an increase in their mass. This is mainly because the interaction between gamma rays and the240Pusample, that is, the self-shielding of gamma rays by the240Pu sample,reduces the total number of gamma rays.The average energy of gamma rays of240Pu estimated by Valentine [8] is 0.95 ± 0.07 MeV, and240Pu is a higher Z material,the photoelectric effect and Compton scattering are the most favorable reactions in this energy region.Therefore, the total number of gamma rays is reduced by the number that have interacted, which also causes the average number of gamma rays to be smaller than that of the240Pu point source in Fig. 1.Similarly,the gamma rays in the240Pu solid sphere are shielded by themselves, and the shielding effect increases with the radius(i.e.,increases with the mass of the240Pu solid sphere).The contributions of other interactions,such as the photonuclear reaction and nuclear resonance reaction,are quite small for gamma rays in the energy range of 0.1–30 MeV, which is less than 1%compared to its self-shielding effect[26].Because the total energy of prompt gamma rays for240Pu(sf)is 6.07±0.03 MeV in Ref. [8], few secondary gamma rays are produced by such processes. Another feature is that the average number of gamma rays for a240Pu solid sphere is smaller than that for a240Pu solid cube with the same mass in the range of 0.05–5.00 kg. The only difference is that the surface area of a sphere is smaller than that of a cube with the same mass.

Table 2 Average number of gamma rays leaking from 240Pu solid spheres and solid cubes with different mass
3 Results and discussion
3.1 Curve fitting
To study the relationship between the average number of gamma rays leaking from a240Pu solid sphere and its mass,an exponential function (y =ae-bx+c) was used, as shown in Fig. 3.When the mass of the240Pu solid sphere is greater than 3.00 kg and less than 5.00 kg,the difference of the corresponding average number of gamma rays becomes smaller and smaller; thus, the average number of gamma rays for the 4.00 kg and 5.00 kg240Pu solid spheres is not used in the curve fitting. The coefficients of the fitting equation are a =1.36, b =2.29, c =1.48, and the correlation coefficient R2is 0.9734. As shown in Fig. 3, the fitting curve agrees with the simulated result in Table 2.
Therefore,it can be concluded from Fig. 3 that there is a one-to-one correspondence between the average number of gamma rays and the mass of the sphere in the range of 0.05–3.00 kg. This provides a method to use the average number of gamma rays to account for the mass of a240Pu solid sphere.Moreover,for240Pu solid spheres in the range of 0.05–3.00 kg, the smaller the mass, the larger the average number of gamma rays leaking from the sphere.However, it is worth mentioning that, as the mass of the240Pu solid sphere becomes close to 3.00 kg, the average number of gamma rays decreases more and more slowly with an increase in its mass.

Fig. 3 (Color online) Fitting curve between the average number of gamma rays leaking from a 240Pu solid sphere and the mass of the sphere,based on data from Table 2
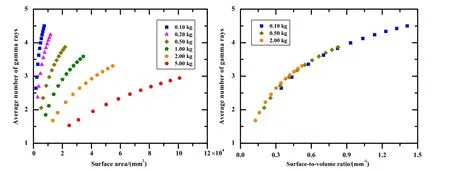
Fig. 4 (Color online) a Average number of gamma rays leaking from a 240Pu rectangular parallelepiped as a function of its surface area.b Relationship between the average number of gamma rays leaking from a 240Pu rectangular parallelepiped and its surface-to-volume ratio
3.2 Average number of gamma rays for 240Pu solid rectangular parallelepiped with different surface area
As the volume is equal for240Pu solid spheres and solid cubes with the same mass, the only difference is their surface area. To study the effect of the difference in the surface area of the240Pu samples on the average number of gamma rays, six families of240Pu solid rectangular parallelepiped with masses of 0.1, 0.2, 0.5, 1.0, 2.0 and 5.0 kg were investigated. To reduce the variable degrees of freedom in the simulation,the lengths of two dimensions in the rectangular parallelepiped were set to be equal, and the other simulation conditions were consistent with those for the solid spheres and solid cubes.The simulation results of the relationship between the average number of gamma rays leaking from the six families of240Pu solid rectangular parallelepiped and their surface area are shown in Fig. 4a.
In Fig. 4a, the average number of gamma rays leaking from a240Pu solid rectangular parallelepiped of a given mass increases gradually with increasing surface area.Meanwhile, the average number of gamma rays leaking from a240Pu solid sphere is less than that from a240Pu solid rectangular parallelepiped of the same mass. Because the gamma rays counted in the simulation leak from the surface of the240Pu samples,the larger the surface area of the240Pu solid samples, the more gamma rays leak out.
In addition, as shown in Fig. 4a, for240Pu solid rectangular parallelepipeds with fixed surface area and varying mass, the average number of gamma rays decreases as the mass increases. On the one hand, for a given mass, the average number of gamma rays leaking from the240Pu solid rectangular parallelepiped increases with the increase of its surface area. On the other hand, for a given surface area,the average number of gamma rays decreases with an increase in the mass (and/or volume). Thus, as shown in Fig. 4b,the average number of gamma rays leaking from a240Pu solid rectangular parallelepiped increases with an increase in the surface-to-volume ratio. The conclusion of Fig. 4b is that the average number of gamma rays is the same for a given surface-to-volume ratio, independent of the specific dimensions. In this regard, because a240Pu solid sphere of a given mass has the smallest surface-tovolume ratio, it emits the smallest average number of gamma rays.
4 Summary
The gamma ray multiplicity of240Pu solid spheres,cubes, and rectangular parallelepipeds is calculated using JMCT, and the corresponding average number of gamma rays leaking from different240Pu samples are also given.In this study, to simplify the effect of the difference in the240Pu shape, the gamma ray multiplicity of a240Pu solid sphere with one degree of freedom (radius) is studied in detail. The relationship between the average number of gamma rays and the mass of the sphere is obtained for240Pu solid spheres with different masses, with the result that the average number of gamma rays decreases exponentially with the increase in the240Pu mass for solid spheres in the range of 0.50–3.00 kg.This result provides a basis for using the average number of gamma rays to account for the mass of a240Pu solid sphere. In addition,the simulation of gamma ray multiplicity leaking from the six families of the240Pu solid rectangular parallelepiped shows that the average number of gamma rays is related to the surface-to-volume ratio.The average number of gamma rays increases with an increase in the surface-to-volume ratio, and will also be constant for a given surface-to-volume ratio, independent of the specific dimensions. Since there is a limited quantity of experimental data on the gamma-ray multiplicity of240Pu samples, to further determine the gamma ray multiplicity of240Pu,multiplicity detectors with high detection efficiency are being studied,and an experiment to measure the gamma ray multiplicity and its average for fission materials is ongoing.
AcknowledgementsThe authors wish to thank the Institute of Applied Physics and Computational Mathematics and the CAEP Software Center for High Performance Numerical Simulation for providing JMCT software and for opening their source interface to us.
Author contributionsAll authors contributed to the study conception and design. Huan-Huan Ding and Chen-Ghang Li conceived the original idea and developed the method. Material preparation was performed by Huan-Huan Ding, Fan Gao, Chang-Bing Lu, Rhi Li and Zhao-Hing Mo. Data collection was performed by Huan-Huan Ding, Fan Gao, Dun-Fu Shi, Ming Su and Chen-Ghang Li.Analysis was performed by Huan-Huan Ding, Chen-Ghang Li, De-Shang Zhao,Mao-Bing Shuai,Zhong-Hua Xiong,Bin-Yuan Xia and Yun Bai. The first draft of the manuscript was written by Huan-Huan Ding, and all authors commented on previous versions of the manuscript. All authors read and approved the final manuscript.
杂志排行
Nuclear Science and Techniques的其它文章
- Spatial resolution and image processing for pinhole camera-based X-ray fluorescence imaging: a simulation study
- Picosecond time-resolved X-ray ferromagnetic resonance measurements at Shanghai synchrotron radiation facility
- Nonrecursive residual Monte Carlo method for SN transport discretization error estimation
- Density fluctuations in intermediate-energy heavy-ion collisions
- Isospin effects on intermediate mass fragments at intermediate energy-heavy ion collisions
- Identification of anomalous fast bulk events in a p-type pointcontact germanium detector
