基于改进向量序优化算法的V2G电动汽车充电站规划方法

2022-07-26周有为高忠江钟雨哲童建林邹红波

智慧电力 2022年7期

周有为，高忠江，钟雨哲，童建林，邹红波

（1.中冶赛迪电气技术有限公司，重庆 400013；2.三峡大学电气与新能源学院，湖北宜昌 443002）

0 引言

十四五规划明确提出要推进“能源革命”与“提倡绿色生产生活方式”，电动车产业作为绿色新能源的重要组成部分，未来必将迅猛发展[1-3]。而电动汽车充电负荷对电网潮流平衡有较大影响[4-5]，同时电动汽车与电网双向能量传输（Vehicle to Grid，V2G），可以有效提升电网的供电可靠性和潮流分布[6-7]。在这样的背景下，亟需提出一种考虑V2G 模式对于配电网动态潮流影响的充电站规划方法。

目前，针对电动汽车V2G 充电站规划的研究，主要集中于V2G 模式下的充放电负荷对于配电网的影响和相应的控制调度策略方面，文献[7]提出一种V2G 模式下城市电网电压质量概率评估方法，在电网运行过程中考虑V2G 模式对于电压质量的影响。文献[8]通过研究电动汽车不同充放电策略下配网潮流变化情况，分析电动汽车与配电网互动时，充放电行为对配电网电压相角、幅值等电气参数的影响。文献[9]则是在直流微电网中考虑电动汽车的影响，将电动汽车作为直流微网中的移动储能看待，构建电动汽车移动储能模型，充分发挥V2G 模式对于直流微电网的优化作用。文献[7-9]的研究均定性或者定量地评估了V2G 模式对于配电网电压等各项指标的影响，但是并没有从配网运行整体角度进行优化。

关于电动汽车充放电负荷对于配电网潮流运行的影响，文献[10]充分考虑大规模电动汽车接入会导致配电网潮流分布发生变化，采用场景概率法进行潮流的计算，并在此基础上确定充电站最优电气接入点。文献[11]采用超立方抽样和场景法建立充电负荷模型，在此基础上进行潮流计算，然后以网损、电压偏差最小为目标函数构建充电站规划模型。文献[10-11]的研究在规划过程中考虑了充电站对于配电网整体潮流运行参数的影响。但是，电动汽车的充电负荷是动态变化的，而考虑充电负荷动态变化和配电网最优安全经济运行模型，构建电动汽车V2G 充电站模型的文章却鲜有报道。

随着经济社会的发展，电动汽车充电站规划过程中，需要考虑的现实因素和电气约束条件不断增多，其规划方案呈指数级增加，而传统智能算法经常面临着收敛和局部最优的问题[12-17]，因此有研究将序优化算法引入多目标优化问题的求解中，其主要思路是通过在算法中构建粗糙评估模型和精确评估模型，实现“目标软化”降低计算量，并在此基础上，有学者提出向量序优化（Vector Order Optimization，VOO）这一算法[18-20]，通过足够好解替代最优解，足够高概率最优解替代确定性解，降低求解难度，提高求解效率。但是目前的向量序优化算法均是采用集中优化的思路进行求解，无法在保证精度同时进一步缩短计算时间。因此本文在向量序优化理论基础上，通过引入分散优化、并行计算的思路，对改造粗糙评估模型进行改进，提出一种考虑分散优化的改进向量序优化算法，进一步提升求解效率。

综上所述，本文对电动汽车可调用的动态功率进行建模，然后构建考虑充电站全寿命周期成本和配电网安全经济运行的多目标规划模型，并采用考虑分散优化的改进向量序优化算法进行求解，和传统的方法相比，本文的主要贡献为：（1）在电动汽车动态功率模型的基础上，充分考虑配电网潮流变化，以考虑V2G 的配电网安全经济运行成本最优为目标函数之一进行规划，提高规划的整体经济效益；（2）在传统向量序优化算法理论中引入分散优化思想，通过对评估模型改造，实现优化过程并行计算，提高了求解效率和精度。

1 多目标规划模型

本文规划模型首先对电动汽车充放电功率动态变化进行建模，然后在此基础上构建充电站规划模型。

1.1 电动汽车动态功率模型

充分考虑电动汽车的移动储能特性，电动汽车不仅仅需要从充电站中获取电能，还可以作为移动储能向电网总释放电能，提高城市电网的潮流分布。在此基础上，构建电动汽车动态充放电功率模型，即：

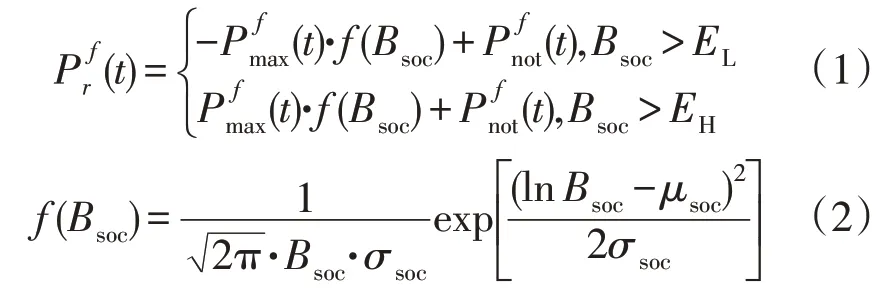
不参与V2G 的充电站的充电能量为：

式中，ζ为用户参与V2G 的概率，是统计学参数；n为所有充电站数量；φ(t)为在t时刻充电站的单位时间充电量；cpi为单个充电站典型模式下的充/放电功率。

单个充电站典型模式下的充/放电功率为：

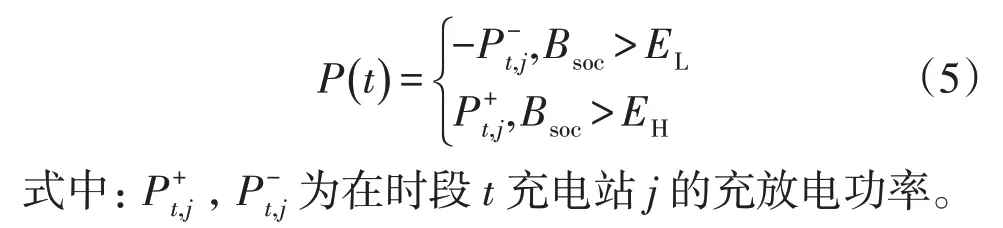
1.2 目标函数

本文选择充电站的全寿命周期成本和考虑V2G 的配网总运行成本作为规划的目标函数。

式中：F为目标函数；F1,F2分别为子目标函数充电站全寿命周期成本和考虑V2G 的配网安全经济运行成本。

1）充电站全寿命周期成本

充电站的全寿命周期成本如式（7）所示。

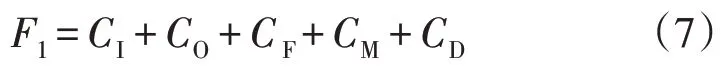
式中：CI，CO，CF，CM，CD分别为初始投资成本、运行成本、故障成本、检修成本、退役成本。

（1）初始投资成本CI的计算为：

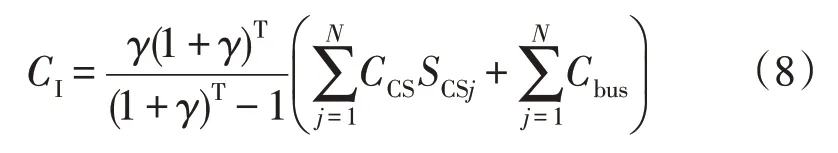
式中：γ为折现率；T为规划周期；CCS为充电站建设费用；SCSi为配网节点i处接入的充电站的容量；Cbus为安装充电站的其他固定成本。（2）运行成本CO为充电站的运行损耗费用。规划周期内目标充电站的运行成本为：

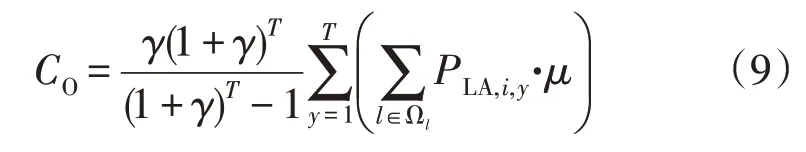
式中：PLA,l,y为充电站i年份y的交换的电量；μ为单位充电量充电站的运维成本。

（3）规划周期内充电站的检修成本为：

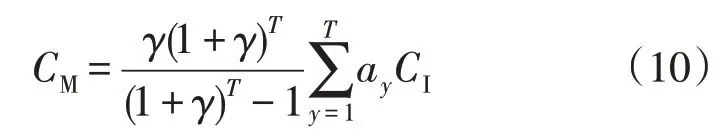
式中：ay为第y年浴盆系数。

（4）故障成本CF指充电站故障引起的经济损失，具体计算方式为：

（5）退役成本CD的计算为：

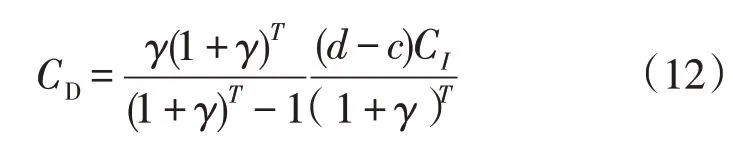
式中：d，c退役成本计算系数，取值分别为0.04 和0.05。

2）考虑V2G 的配电网安全经济运行成本

考虑V2G 配电网安全经济运行成本模型是在引入V2G 后，在保证配电网系统安全运行的前提下，总运行成本最小，其目标函数为：

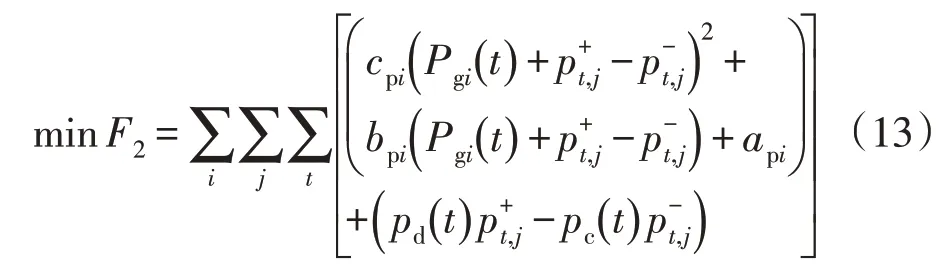
式中：cpi，bpi，api为节点i购电成本参数且为定值；Pgi为节点i购电量；为电动汽车充、放电电价。

1.3 约束条件

1）有功功率平衡约束

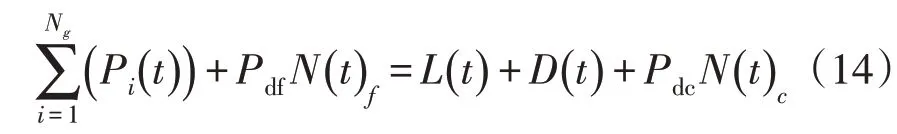
式中：Pdf为电动汽车平均放电功率；L(t)为网损；D(t)为预测得到的有功负荷；Pdc平均充电功率；N(t)f，N(t)c为t时刻充、放电车辆数。

2）充放电约束

电动汽车的充、放电功率均应小于充电站容量，即：

3）节点电压约束

4）支路电流约束

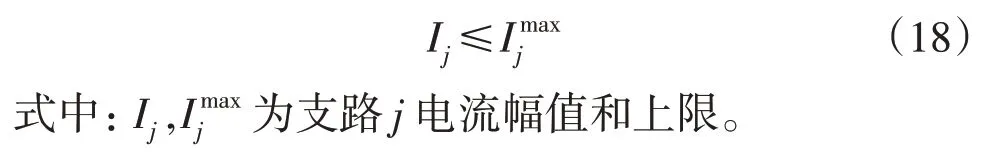
2 基于改进向量序优化算法的模型求解

本文改进向量序优化算法[18-20]通过引入目标级联分析理论对粗糙模型进行分散优化，并列计算，进一步提高求解效率。

2.1 改进向量序优化算法的优化原理

本文改进向量序优化算法针对传统向量序优化算法中粗糙评估模型构建问题，通过引入目标级联分析进行分散优化，提高计算效率，本文提出的改进思路如下图1 所示。

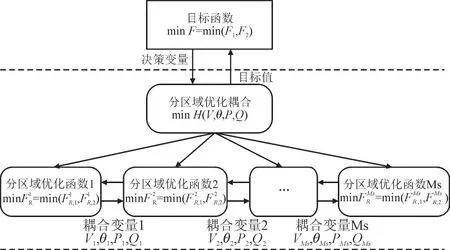
图1 算法改进思路图Fig.1 Diagram of algorithm improvement

2.2 改进向量序优化算法的粗糙评估模型

1）粗糙评估模型的目标函数

本文首先以电动汽车充电站最大接入容量为决策变量，通过潮流计算，以充电站建设成本和总体运行成本最小为目标函数构建粗糙评估模型[21-23]，即：

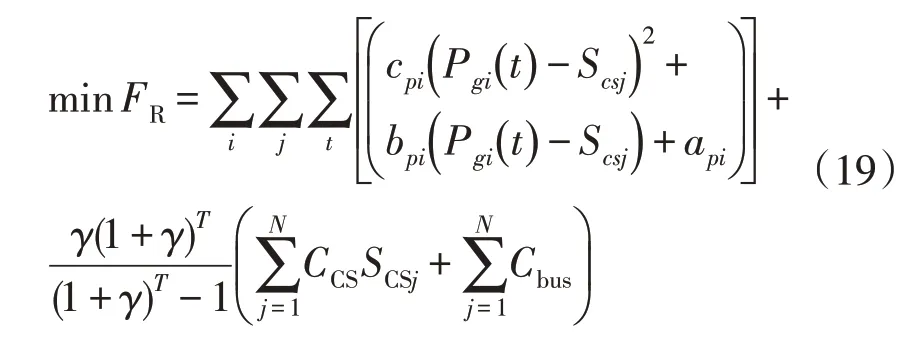
式中：FR为粗糙评估模型。

2）分散式优化粗糙评估模型

在粗糙评估模型目标函数的基础上构建分散优化粗糙评估模型，将式（19）进行区域解耦，进行分区域优化，并列求解，耦合变量为电压幅值V、相角θ、有功功率P、无功功率Q，即：

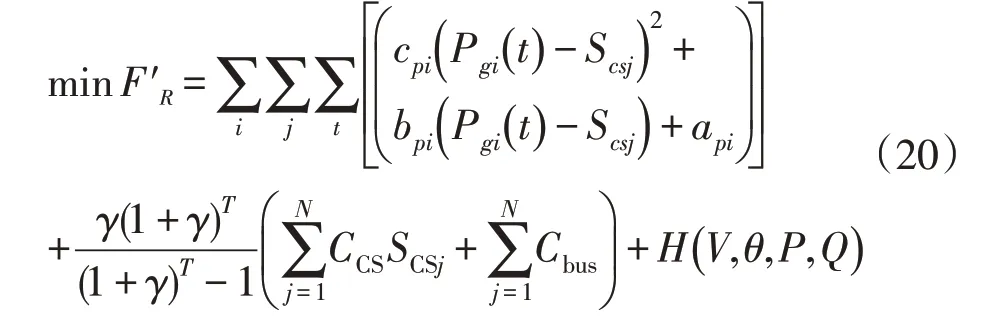
分区域耦合模型H()V,θ,P,Q的计算如式（21）所示：

2.3 改进向量序优化算法的算法流程

在分散优化粗糙评估模型的基础上，得到改进向量序优化的求解流程。具体求解步骤为：

步骤1：初始化，生成规划方案，在此基础上得到规划方案集的表征集合。

步骤2：对表征集合进行分散区域粗糙评估，评估模型如式（20）所示，针对各个区域，以V,θ,P,Q为返回值进行迭代计算并判断收敛，收敛判据如式（22）所示。根据排序分层算法进一步得到表征集合的序曲线（Ordered Performance Curve，OPC），确定优化问题类型，即：

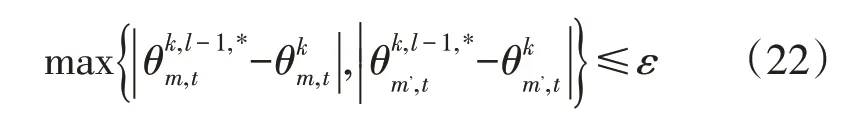
式中：ε为收敛条件，取0.004。

步骤3：确定精确评估集合S，取表征集合前s层为选定集合S。其中s的计算为：

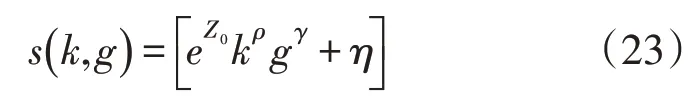
式中：s为关于κ，g的函数，其中κ为帕累托解，g为帕累托解的层数；e为自然对数；Z0，p，r为回归参数；φ为噪声分量[19]。

步骤4：采用式（6）对集合S进行精确计算，然后对计算结果进行第二次排序分层，得到帕累托前沿。

步骤5：比较帕累托前沿的充电站全寿命周期成本和配电网运行成本，得到最优规划方案。

3 算例分析

3.1 算例说明

本文IEEE33 节点仿真算例包含33 个节点和32 条线路，其中各个节点均可接入V2G 充电站[24-25]。

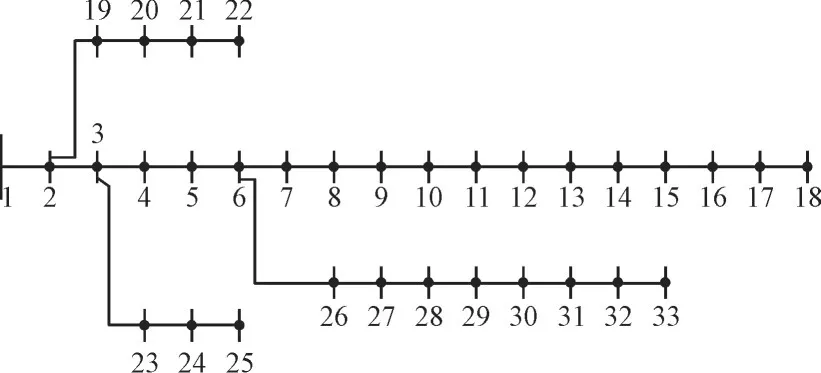
图2 IEEE33节点配电系统Fig.2 IEEE33 power distribution system

在IEEE33 节点配电系统基础数据上，充电站典型日的电动汽车的充电行为和数量利用蒙特卡洛方法进行模拟得到，在此基础上结合电动汽车可调用负荷进行潮流计算。

3.2 算例结果

通过改进向量序优化算法计算得到本文算例的OPC 曲线，进而确定了其优化类型为natural 型，其中OPC 曲线如图3 所示。

图3 OPC曲线Fig.3 OPC curve

此基础上，由公式（23）计算得到s＝2，即集合S的前两层为可行解的帕累托前沿，具体计算结果如表1 所示。

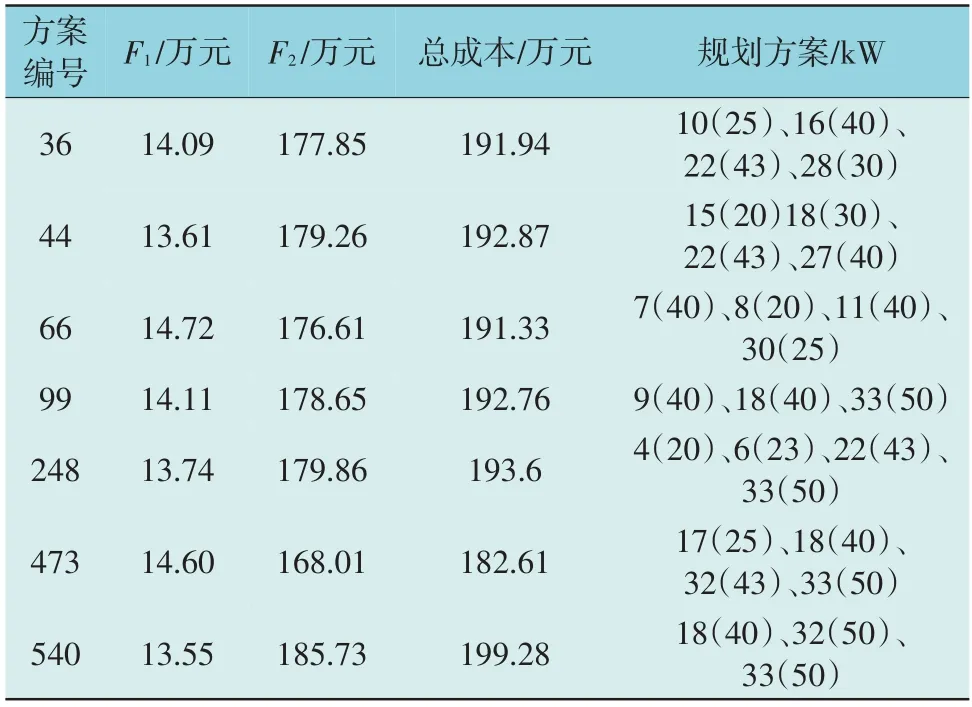
表1 可行解的帕累托前沿Table 1 Pareto frontier of feasible solution

由表1 可知，从总体成本看，在帕累托前沿中，本文算例规划方案最优解为473 号解，其具体规划方案为：17，18，32，33 节点安装容量分别为25 kW，40 kW，43 kW，50 kW。规划方案中括号前面的数字为编号，括号中的数字为安装容量。

3.3 算例分析

1）结果分析

由计算结果可知，考虑V2G 的电动汽车充电站在电网中以不同的方式和容量接入，对电网的运行参数均有不同的影响。如图4 所示，本文规划方案使得充、放电负荷可以有效进行配电网负荷的削峰填谷。如图5 所示，由于电动汽车充放、电负荷的影响，导致配电网各节点潮流发生变化，同样引起了配电网网损的变化。

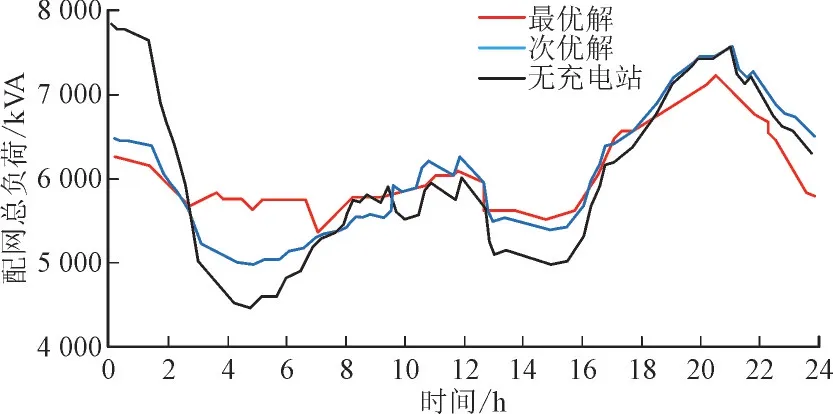
图4 负荷优化图Fig.4 Load optimization diagram

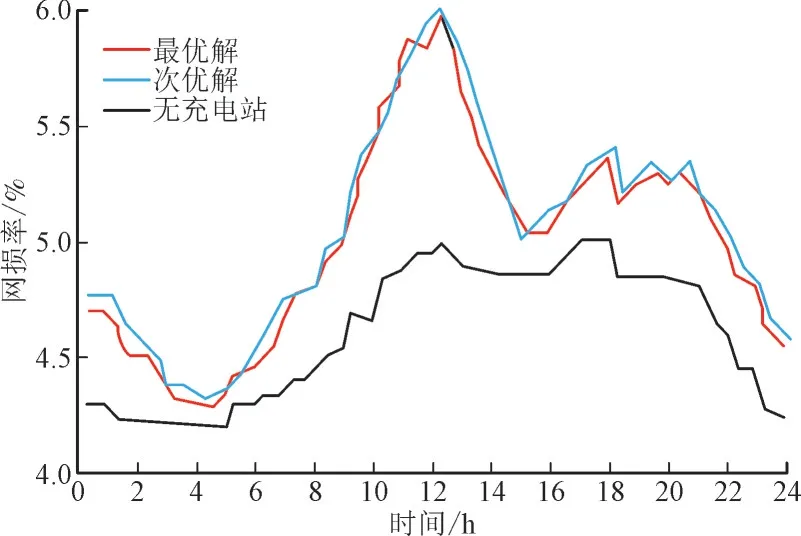
图5 网损优化图Fig.5 Network loss optimization diagram

进一步分析图4、图5 可知，最优解和次优解相比，对于负荷和网损的影响程度并不相同，通过表2对各参数的影响程度进行量化分析，首先对于负荷影响程度，最优解的负荷标准差为1 978.6kW，相较于次优解的2 189.4kW 降低了210.8kW，最优解平衡配电网负荷的作用更加显著；与此同时，最优解的平均线损率较次优解同样减小了0.82%，在相同的充、放电负荷下，最优解对于配电网网损的影响程度更小。对比最优解和次优解的规划方案可知，二者主要的区别在于充电站接入位置不同，最优解电动汽车充电站的接入位置为IEEE33 节点系统馈线后半段，其主要原因是：由于线路损耗等原因，导致线路末端电压质量更易受到影响，造成系统潮流分布不均衡。最优解通过一定的投资成本增加，通过合理选择充电站位置，优先选择在线路的末端进行V2G 充电电站规划，通过调度和消纳电动车的放电功率，改善配电网的潮流分布，优化了网损指标，降低了接入充电站后配电网整体的运行成本。