基于合同功率与持续时间的电网老化和可靠性优化

2022-07-26董飞飞张云晓张天龙何天宇邹红波

智慧电力 2022年7期

董飞飞，刘欣，张云晓，张天龙，何天宇，邹红波

（1.电力规划总院有限公司，北京 100120；2.三峡大学电气与新能源学院，湖北宜昌 443002）

0 引言

电力网络致力于以安全，可靠和经济的方式输送电力。不断完善的市场法规和高昂的电网建设费用将进一步阻塞电网向可再生能源扩展的需求[1-3]。电力企业亟需研究和实施更加灵活的架空线路网络增强策略，这些策略可以提高网络功率传输能力，同时避免不必要的重大资产投资[4-6]。

使用基于需求响应（Demand Response，DR）程序补偿[7-8]、基于架空输电线（Over-Head Line，OHL）的热行为[9-10]来增强其额定值。DR 补偿是根据需求侧进行调控，研究已较为成熟。热额定值提升是从供给侧入手，形成了2 种灵活的热额定值：动态线路额定值（Dynamic Line Rating，DLR）系统和概率热额定值（Probabilistic Thermal Rating，PTR）方法，实施PTR 可能会增加线路老化的风险，破坏OHL 的实际容量。DLR 方法始终可以根据所选导体温度实现最大线路额定值。但确定导体最佳温度的风险尚未被电力企业量化。文献[14]基于计及老化风险的电网预防控制模型，引入支路开断分布因子，提高了模型求解效率和网络可靠性。文献[15]考虑了由于DLR 方法引起的OHL 线路的老化效应及其参数对线路失效概率的不确定性。文献[16]考虑了使用PTR 方法操作的OHL 老化对网络可靠性的影响。文献[17]基于电缆所接负荷的特性，通过接地电流的变化分析了电缆绝缘老化程度，但并未对可靠性展开研究。文献[18-19]对配电网中的电缆老化进行了建模，并根据老化临界程度对电缆进行排序，以确定实现最佳网络可靠性的电缆更换优先级。这些研究提出了OHL 和电缆的各种老化模型，论证了老化对网络可靠性的影响。但尚未有文献考虑过网络老化和可靠性之间的折衷问题。

本文首先提出了一个将DLR 和DR 评估集成的优化框架，该框架新颖之处在于对合同功率和持续时间（Contractual Power and Duration，CPD）的最佳利用，在不引起过度老化的前提下提高网络可靠性。然后对优化框架中的各模块功能和建模细节进行了介绍和说明，基于初步筛选模块研究了应急DR 方案的自动响应，确定了CPD 的初始优化值，代入执行模块解决了网络可靠性与老化之间的权衡问题。最后与仅考虑可靠性或老化的方案进行对比分析，说明了所提出方法的优越性。

1 研究方法

提出的可靠性评估框架如图1 所示。所使用的网络数据包括母线电压限值、发电机功率限值、每小时按时间顺序的负载需求模式、描述所有线路、电缆、变压器等电力元件布局的网络拓扑以及基于操作员历史记录的每个元件的可靠性数据。OHL 数据包括各种设计因素，例如直径、低温和高温下的电阻、股数、额定强度和导体类型等。天气数据包括风速、风角、环境温度以及太阳辐射角和强度等。

图1 DR和DLR协同优化网络可靠性和老化流程图Fig.1 Flowchart of proposed DR and DLR synergy for optimum network reliability and aging

在初步筛选模块中，执行经典的顺序蒙特卡罗（Sequential Monte Carlo，SMC）模拟[20-23]。在SMC 的每个模拟时间步长Δt处，执行标准的最佳交流功率流（Alternative-Current Optimal Power Flow，ACOPF），将跟踪每个负载母线上未供给的预期能量EENS（Expected Energy Not Supplied，EENS）来进行仿真，直到EENS 的值SEENS满足系统EENS 收敛为止。另外，还记录了每条负载母线上的负载削减的预期持续时间EDLC（Expected Duration of Load Curtailment，EDLC）和预期频率EFLC（Expected Frequency of Load Curtailment，EFLC）。EDLC 的值用TEDLC表示，EFLC 的值用PEFLC表示。将负载母线b的合同功率PCP_b和持续时间TCD_b传递到执行模块进行处理，获得DR 和DLR 的最佳比例，以最大程度地减少系统SEENS和预期的总网络老化（Expected Total Network Aging，ETNA），ETNA 的值用SETNA表示，计算为：

在每个Δt处的执行模块都是从检查意外情况开始的，基于CPD 值的最佳用法确定提升后的DLR值ADLR_new和负载需求新模式DRnew，并执行ACOPF。然后，检查DLR 提升所考虑的每个OHL的导线温度Tc的增量，即超过其老化温度Tage的部分[24]，获得的Tc用来确定OHL 的老化因子。SMC的迭代模拟状态都会考虑OHL 的工作温度和剩余使用寿命。在模拟收敛后，计算网络SEENS和SETNA，这2 个目标参数也被用作优化算法检查指定功能公差的停止标准。只要不满足协方差（Covariance，COV），就选择下一个合同功率百分数α继续重复该过程执行模块中提到的各种优化方案。

2 模型建立

2.1 负荷需求模型

根据DR 聚合器在每条负载母线意外事故期间利用合同功率CPb的可靠性和DR 聚合器介于0 和1 之间的均匀随机可用性系数u，在时刻t处的可用合同功率PCP_b（t）的计算为：

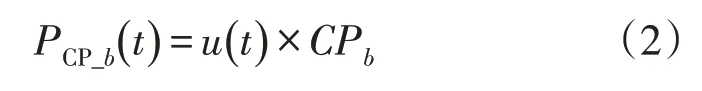
使用超过峰值负载Lb_peak的原始负载需求水平百分数l和PCP_b（t）的降低百分数αb来执行修改，即：

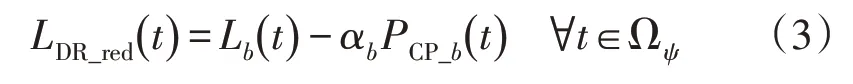
式中：LDR_red（t）为发生负载减少时所有时间的新负载需求；Ωψ为时的时间集合；Lb()t为原始负载需求水平。

通过在总线的合同期限TCD_b中将它们均分，可以在下1 个小时将负载恢复为：

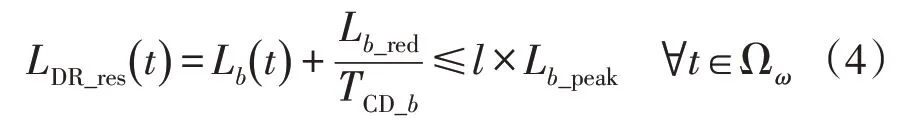
式中：LDR_res（t）为发生负载恢复时所有时间的新负载需求；Ωω为时的时间集合，使得k＜l以确保恢复后不会产生新的峰值；k为低于峰值负载Lb_peak的原始负载需求水平百分数。

2.2 线故障模型与老化模型

将OHL 使用寿命与其热应力联系起来的最为常见模型是Arrhenius，模型为：

式中：L为OHL 的平均寿命测量值；A，B 为采用历史数据导出的经验常数。

所选择的威布尔分布函数应仅有1 个寿命度量，且参数可以捕获响应更高的线路负荷和有用寿命而增加的故障率，根据文献[25]得到威布尔失效概率U，计算出的失效概率U和修复率固定值μ最终用于推导与寿命和载荷相关的OHL 失效率λL。

当OHL 在超过老化温度Tage的温度下运行时，导线就会加速老化，将不同Tc下的不同蠕变εc值归一化为Tc=100 ℃下的等效老化t100，以获得所有导线之间的可比老化为：

式中：RSTc为温度Tc下导体剩余强度的百分比；ε100为OHL 在100 ℃下的蠕变。

根据所有模拟年份Ny中所有OHL 中所有不同的衰老事件，确定了SETNA为：

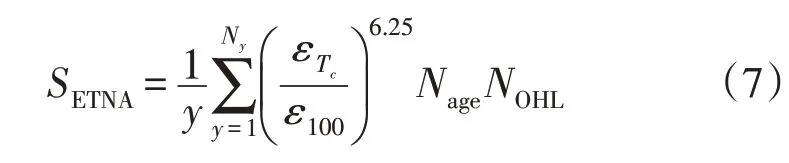
式中：NOHL为OHL 总数；Nage为OHL 中发生的老化事件。

2.3 优化模型

因此，在每个Δt期间，SEENSb和SETNAb这2 个指标更适合作为双目标函数最小化来解决，即：

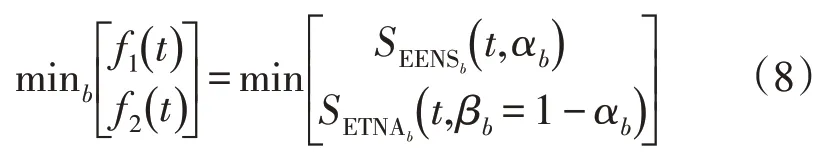
鉴于需求损失的减少和DLR 的增加都是基于使用PCP_b来实现的，因此始终保持关系αb+βb=1。以下是所提出优化模型的2 个目标详细信息，βb为母线b合同功率的百分数。

目标1：根据合同功率所使用的电力比例，将电网的SEENS降到最低，即：

式中：Pb_loss为ACOPF 期间通过考虑OHL 的DLR 提升而确定的负载母线b的减载；Nb为负载总线数。

目标2：根据使用的合同功率的剩余比例来最小化电网的SETNA。第二个目标函数为：

式（10）表示考虑所有OHL 的线路额定量增量ΔADLR()t,βb后计算的SETNA，这个指数量化了网络的额外允许潮流，即：

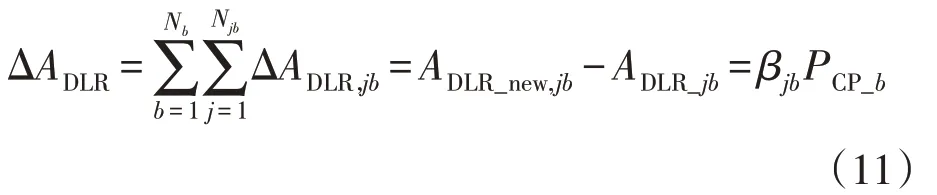
式中：Njb为母线b的馈线j的总数；ΔADLR，jb为母线b的馈线j额定值的增量；ADLR_new，jb为在DLR 提升后馈线额定值；ADLR，jb为在DLR 提升前馈线额定值；βjb为负载总线b的所有馈线中βb的均分。

SETNA(t,β)的解需要确定DLRnew的等效运行温度Tc，由于热平衡方程非线性，在已知变量相同的情况下，反向计算该方程以确定满足热平衡方程的Tc。从Tc=Tair（环境温度）开始，Tc在每次迭代中增加0.5 ℃，然后重新进行计算。当连续的热平衡误差小于1%时，将终止此反向计算过程。

2.4 决策模型

模糊决策法通过确定每个解与最大值和最小值的相对距离来判断，其中0 和1 分别表示最不期望和最期望的解，点X在目标i的最大解和最小解之间的相对距离μfi()X为：

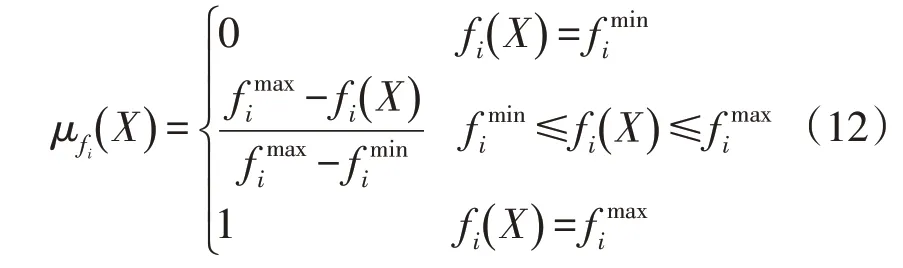
最终点x选择为：

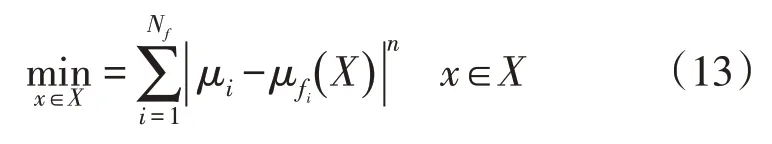
式中：Nf为解的数量；μi为解的优先级；n为1 到∞之间的整数。

3 结果分析

将所提出的优化方案在IEEE 24 总线可靠性测试网络（Reliability Test Network，RTN）中加以应用。DR 方案是在RTN 峰值负载l=80%和k=60%时实现的。初步筛选模块中确定的CPD 值PCP_b和TCD_b如图2 所示，它们的值是相互匹配的，并用作执行优化模型中的优化基础。假设文中所使用的架空导线的老化温度为95 ℃，当温度超过这个限值后，超出的温度仅被限制为该值的15%，且不考虑网络中变压器和地下电缆的可靠性和老化问题。

图2 初步筛选模块确定的CPD值Fig.2 CPD values identified in initialisation module

3.1 CPD值的优化使用

图3 中的第一个Pareto 解是在优先考虑系统可靠性的情况下获得的，PCP_b全用于提高DLR 的效率，而不关注过度负载引起的线路老化。在最优先考虑网络老化的情况下，可以获得第二个Pareto解，完全避免了线路老化，并且PCP_b仅用于DR 动作。较高的SEENS值表明，尽管DR 方案能够通过均衡峰值负载来减轻发电机的负担，但其对系统可靠性的好处却受到电力网络传输能力瓶颈的限制。

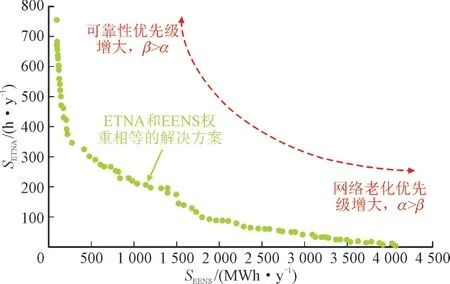
图3 优化方案的帕累托解Fig.3 Pareto front of proposed optimisation

EENS 和ETNA 基于等偏好设置（μ1=μ2=0.5）选择的各负载母线的最优αb和βb值如图4 所示。

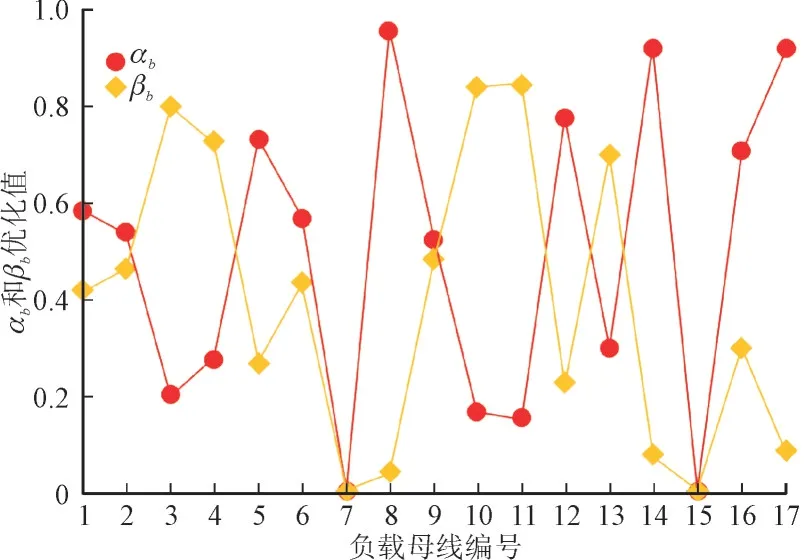
图4 基于等偏好设置的各负载母线α和βFig.4 Optimal values of α and β of each load bus based on equal preference settings

母线3，4，10，11 和13 利用较大比例的PCP_b（βb＞0.5）来提升与它们相连的线路DLR 值。母线3，4 和10 上的累积负载平均占网络总负载的15.7%，且均无本地发电机，迫使所有负载需求只能通过从远程母线上的其他发电机输入功率来获取。这些负载母线大多数时候至少与两条馈线连接，不会因线路共享分担的负荷上调而导致过度的线路老化。负载母线11 和13 具有本地发电机，在满足本地需求后仍有很大的盈余，可将剩余功率传输到其他母线。母线11 和13 至少与2 个输出线路连接，可分担上调的负载。其余的负载母线1，2，5，6，9，12，14，16 和17 将大部分PCP_b值（αb＞0.5）专用于DR 动作，这些负载母线需求小，提高其连接线的ADLR的必要性较小，并且DR 动作足以减轻这些负载总线上的SEENS。负载总线7 和15 被排除在优化之外，这是因为它们上没有CPD 值。

3.2 优化方案的可靠性影响

优化方案如表1 所示，并对它们的可靠性影响进行了比较。A1 是基本情况，不使用任何CPD 值来增加灵活性。A2 在不考虑网络老化的情况下将系统可靠性降至最低。A3 忽略了系统可靠性，只寻求网络老化最小化。A4 是在模糊决策模型中提出的具有等偏好设置的优化。除了SEENS和SETNA，还记录了预期中断成本EIC（Expected Interruption Cost，EIC）和预期总网络成本ETNC（Expected Total Network Cost，ETNC）等新指标，EIC 的值用CEI表示，ENTC 的值CENT表示。

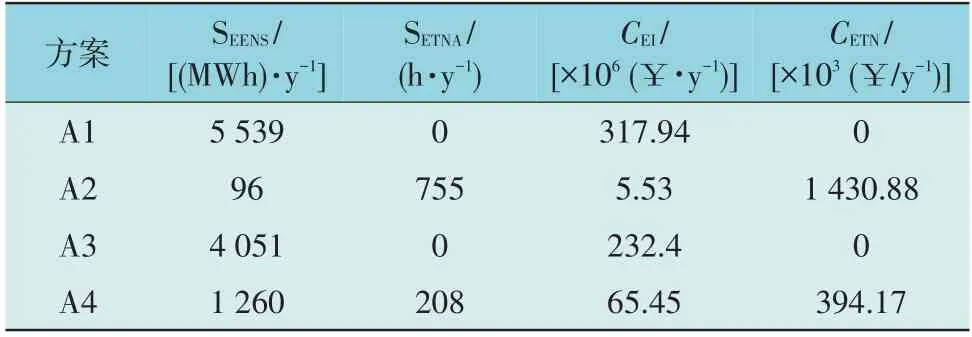
表1 可靠性指标Table 1 Reliability indices

A1 中OHL 的温度限制为95 ℃，且没有使用任何CPD 值来降低峰值需求。因此A1 的SEENS和CEI最高，分别为5 539 MWh/y 和317.94×106￥/y。当使用CPD 值平衡A3 中的峰值需求来增加RTN 灵活性时，SEENS和CEI与A1 时相比显著下降了26.9%，但没有采取主动措施提升线路的DLR，因此A3 中未出现任何网络老化情况。相比之下，A2 将所有CPD 值用于提升DLR，但峰值需求并未减少。导体温度将升高到老化温度95 ℃以上，以确保所产生的功率通过最佳的传输途径传递到每个负载点，A2 中的SEENS最低，但SETNA却被提高到755 h/y，与A1 和A3 相比，其成本约为1 430.88×103￥/y。A4 不仅是单独降低了SEENS或SETNA，而是基于所提出的优化模型将两者均最小化。尽管此时SEENS大于A2，但其值仍远远低于A1 和A3 的SEENS，减幅分别达到了A1的77.3%和A3 的68.9%。就SETNA而言，A4 的网络老化也约比A2 低72.5%，可节省1 036.28×103￥/y，弥补了CEI值的59.92 M￥/y 增长。

3.3 导体温度超标影响

导体温度的超标极限范围为老化温度的1%到25%，其余所有其他设置都相同。由于导体温度仅会影响到网络老化，仅A2 和A4 受到影响，如图5所示。

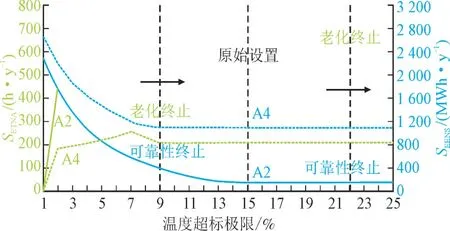
图5 温度超标极限对SETNA和SEENS的影响Fig.5 Exceedance effects on SETNA and SEENS

由图5 可知，A2 和A4 中的SETNA都随着超标百分比的增加而增加，而它们的SEENS却随着超标百分比的增加而减小，呈负相关。由于A2 忽略了线路老化并仅优先考虑系统可靠性，因此在整个研究的超标范围内，它的SETNA高于A4，SEENS低于A4。但A4 中的2 个指标在超过9%后保持恒定，而A2 在超过22%后才停止。主要原因是用于提高DLR 的合同功率PCP_b的比例在这些点上被完全使用，进一步提高超标极限对DLR 不再有影响。A2 具有更高的线路升级潜力，与A4 中的9%相比多出了13%，以便完全消耗掉PCP_b。

SETNA分别在A4 和A2 中趋于平稳之前分别下降了7%和21%。在达到平衡之前，线路额定限值低于专门用于线路升级的PCP_b。因此，线路额定限值在提升后总是达到上限，只有通过提高超标水平才能进一步提高。但当超过这些点后，线路额定值限值被解锁以分担上调负担，从而导致SETNA在与PCP_b全用于线路上调之前相比略微降低。结果表明，在任何特定的超标水平下，A4 的老化平均比A2低70.3%，因此A4 允许更高的线路容量，同时显著降低老化风险。