基于时序动态回归的超短期光伏发电功率预测方法

解振学，林 帆，王若谷，张 耀，高 欣，王建学

（1.国网陕西物资公司，陕西西安 710054；2.陕西省智能电网重点实验室，西安交通大学陕西西安 710049；3.国网陕西电力科学研究院，陕西西安 710100）

0 引言

近年来，我国可再生能源产业，尤其是光伏发电产业发展迅猛。截至2019 年底，全国可再生能源发电装机总容量已达7.94×108kW，占全部电力装机的39.5%，其中，光伏发电装机容量为2.04×108kW，同比增长17.3%[1]。在国家政策影响下，分布式光伏发电增长尤为迅速，截至2019 年底，全国分布式光伏累计装机已达6.263×107kW，同比增长24.2%，2019年内的增长容量为1.220×107kW，同比增长41.3%[2]。

光伏发电功率预测可以根据预测提前期划分为超短期、短期、中长期预测等。超短期预测主要关注未来数小时内的光伏出力情况，对于日内的电网调度计划调整与电力市场交易具有重要指导意义。

目前超短期光伏发电功率预测的实用方法主要有2 类：（1）结合气象云图分析的预测方法；（2）基于数据驱动的预测方法[3]。在基于云图的预测方法中，文献[4]描述了一种以卫星云图与地面遥感数据作为输入的人工神经网络模型，预测提前期为2 h。文献[5]结合卫星云图与数值天气预报结果进行了提前期为4 h 的光伏功率预测。除卫星云图外，地基云图也有所应用。文献[6]根据地基云图与数值天气预报进行了未来4 h 内的光伏功率预测。文献[7]介绍了位于美国San Diego 的地基云图分析系统，并用该系统对未来15min 内的太阳辐照度进行准确预测。文献[8]以实时采集的全天空图像和太阳辐照数据作为输入，预测未来1～10 min 内的每分钟平均太阳辐照。在数据驱动型的预测方法中，文献[9]基于动态人工神经网络方法进行提前1 h 的光伏功率预测。文献[10]则采用改进的共轭梯度算法对动态神经网络光伏功率预测模型的训练进行优化，获得了精度较高的预测。文献[11]基于以气象信息为主要特征的光伏功率相似日思想，采用动量优化方法训练BP 神经网络预测模型。类似地，文献[12]在相似日历史数据的基础上，采用回声状态神经网络建立了光伏功率短期预测模型。除单一的非线性预测方法外，组合方法也得到广泛研究。文献[13]混合AR 模型和Lucheroni 模型[14]提出了CARDS 模型，用于预测未来数小时内的太阳辐照强度。文献[15]结合小波变换技术与人工智能技术，进行了提前1 h 的光伏功率预测。文献[16]采用深度信念网络进行光伏发电功率短期预测，并通过粒子群算法对神经网络的训练过程进行优化。文献[17]采用模糊技术挖掘历史数据的规律，配合在线加性学习，滚动预测未来数十分钟内的光伏发电功率。文献[18]使用Elman 神经网络[19]进行光伏功率短期预测，并采用改进的布谷鸟算法[20]对Elman 神经网络预测模型的结构与状态进行优化。文献[21]采用加入Soft attention 机制的双向LSTM 模型[22]作为光伏发电量预测模型，并使用粒子流算法优化预测模型参数。

文献[3-21]所提出的光伏发电功率预测方法都在气象数据采集与存储方面存在较高要求，而我国光伏发电产业的现状是配套的气象观测设备普遍不完善，没有上述预测算法所需要的高精度气象观测数据。

因此，本文提出了一种基于时序动态回归的超短期光伏发电功率预测方法，仅需要历史光伏发电功率数据与数值天气预报作为输入，即可获得较高精度的预测结果。算例结果表明：在原始数据集相同的情况下，与一般时序模型相比，本文提出的模型在超短期预测上的预测精度明显更高。

1 光伏功率数据来源及数据相关性分析

本文所使用的光伏功率数据来源于澳大利亚某光伏电站（149°E，35°S）[23]，数据范围为2012 年4月至2013 年6 月，共计447 d，等距采样间隔为1 h。数据集包括2 部分：（1）归一化的光伏电站实际发电功率；（2）欧洲中期天气预报中心提供的数值天气预报（Numerical Weather Prediction，NWP），其中与光伏发电最相关的气象要素为地表太阳辐射累计值（Surface Solar Radiation Down Accumulation，SSRDA）。2 部分数据的时间分辨率相同，在分析前，数据均已经过归一化处理。

1.1 光伏发电功率与SSRDA的相关性分析

原始的SSRDA 数据为每小时累计值，对其作差分后获得每小时辐射量（Hourly Surface Solar Radiation Down，HSSRD），其量值记作HSSRD。与光伏发电功率直接联系的是同时刻的太阳辐射强度，对HSSRD 作二阶滑动平均可以更好地近似这一物理量，如式（1）所示，得到新时间序列平滑后每小时辐射量（Smoothed Hourly Surface Solar Radiation Down，SHSSRD），其量值记作SSSRD。其与光伏发电功率数据的相关性如图1 所示。根据图1 数据，SHSSRD 与光伏发电功率的相关系数为0.877，两者表现出较强的相关性。

图1 SHSSRD与光伏发电功率的散点图Fig.1 Scatter plot of SHSSRD and photovoltaic power

式中：t为时间刻度。

除了图1 所展示的线性相关性以外，光伏发电功率与SHSSRD 的相关性也可能表现为非线性形式。通过将二者分别作自然对数变换，得到如图2所示的散点图。

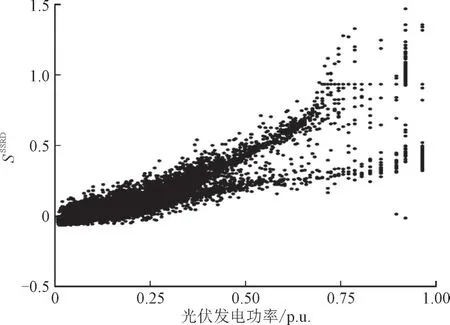
图2 SHSSRD与光伏发电功率经对数变换与-0.1倍伸缩后的散点图Fig.2 Scatter plot of SHSSRD and photovoltaic power after log-transformation and multiplying by-0.1

为了方便展示，图2 中的数据经过了-0.1 倍的伸缩，这一操作不影响数据相关性。根据图2 数据，经自然对数变换后，SHSSRD 与光伏发电功率的相关系数增加到0.945，说明SHSSRD 与光伏发电功率的相关性具有显著的非线性特征。图2 最右侧的数据点比较分散，这是因为这些点对应着原数据中光伏发电功率接近于0 的部分。

1.2 光伏发电功率的季节性分析

因为太阳日升日落及太阳高度角随季节变化的自然规律，光伏发电功率时间序列具有复杂的季节性。将光伏发电功率全体数据按照1 d 中不同的时刻加以分类，得到箱线图如图3 所示。

图3 光伏发电功率按照1 d中不同时刻分类的箱线图Fig.3 Box plot of photovoltaic power classified by different time of day

图3 描绘了各分类子集的中位数、上下四分位数、最小最大值等统计指标。据此判断，光伏发电功率的时间序列具有明显的日季节性。另外，将光伏电站全天发电量按月份分类，得到的箱线图如图4 所示。从图4 可以看出，光伏发电功率时间序列也具有较为明显的年季节性。

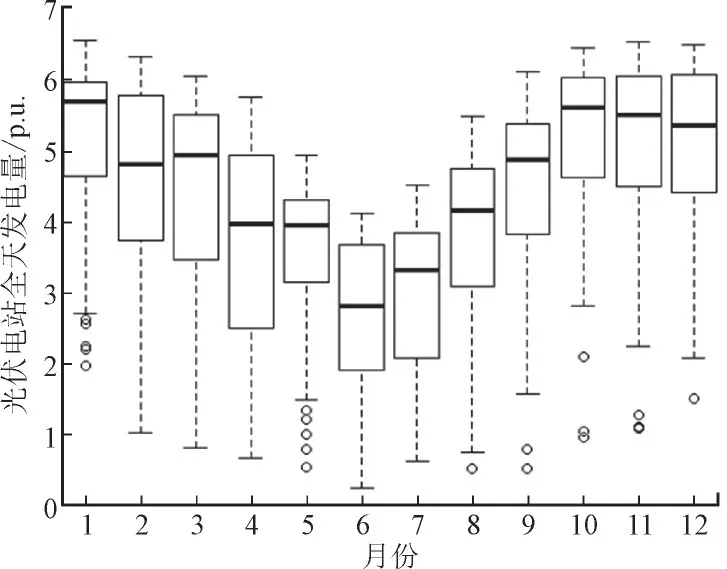
图4 光伏电站全天发电量按照月份分类的箱线图Fig.4 Box plot of daily electricity generation from solar power station by month

2 时序动态回归预测模型

2.1 简单回归模型

根据1.1 节的相关性分析结果，可基于回归原理选择SHSSRD 数据作为输入变量，来预测光伏发电功率，回归方程可写为如下2 种形式：

式中：Pt为t时刻光伏发电功率；β0为回归截距；β1为回归斜率；εt为回归残差。

式（2）和式（3）的结构相同，都是线性回归模型，只是式（3）中经过了对数变换，因此将式（2）称为回归模型的普通形式，式（3）则称为对数形式。无论哪种形式，简单回归模型只能捕获时间序列中蕴含的部分信息，残差项εt仍然保留着大量未被充分利用的信息。

2.2 整合移动平均自回归模型

残差信息的挖掘对于提高回归类预测模型的预测精度具有重要意义。而且，残差项本身就是一个时间序列，本文采用整合移动平均自回归模型（Autoregressive Integrated Moving Average，ARIMA）对上述回归模型的残差项进行建模预测[24]。

1）平稳时间序列的获取方法。ARIMA 方法只能应用在平稳时间序列上。平稳序列是指类似于白噪声的无明显趋势性与季节性的时间序列。然而，式（2）和式（3）中含有规律信息的残差εt仍然可能不是平稳时间序列，此时需要通过差分运算获得平稳序列。这里给出时刻后移算子B，如式（4）所示：

式中：εt-1为t-1 时刻的残差项。

2）自回归模型（Autoregressive Model，AR）与滑动平均模型（Moving Average Model，MA）。在获得平稳时间序列后，可以选择AR 预测模型或MA 预测模型。AR 模型是利用历史数据的加权平均进行预测，如式（5）所示：

式中：yt为回归残差经过可能的差分运算后获得的平稳时间序列；c为常数项；φi为历史数据yt-i的权重；p为正整数；et为预测误差。

MA 模型则是利用历史预测误差的加权平均进行预测，如式（6）所示。

式中：θi为历史预测误差et-i的权重；q为正整数。

式中：f为数学变换，这里可以取恒等变换（对应回归方程式（1）），也可以取对数变换（对应回归方程式（2））；Bi为后移算子的i次方，表示将时刻后移i个单位，i为自然数；ηt为ARIMA 部分的预测误差。

2.3 季节性谐波分量

由于SHSSRD 数据来源于数值天气预报，不可避免存在误差，因此在刻画光伏发电功率序列的季节性方面（见1.2 节），完全依赖对SHSSRD 进行回归并不可取。为了准确刻画光伏发电的季节性特征，本文引入谐波分量作为额外的预测变量，以配合ARIMA 方法挖掘原始回归残差中剩余的季节性特征。

对于季节性周期为m的时间序列，可以定义如式（8）所示的1 组谐波分量：

式中：k为谐波次数；x2k-1,t，x2k,t分别为第k次谐波分量的余弦部分与正弦部分；K为谐波最大次数，1≤K≤0.5m。

值得注意的是，K若取值较大，不仅会使运算量大幅增加，还可能导致过拟合问题，因此K并非越大越好。另外，因为SHSSRD 数据对光伏发电功率的年季节性已经有所体现，而且在超短期预测中，年季节性的影响要远小于日季节性，所以这里只引入m=24 的谐波分量以刻画关键的日季节性。

根据式（7）和式（8），可得到考虑季节性谐波分量的动态回归模型，如式（9）所示：

老式B-29、B-59型轰炸机夜以继日地将多达百万吨的炸弹扔在北越的公路上，第二天早晨你就会发现越南人又在上面通过了……尽管美国拥有绝对的制空权和制海权，但实际上从未有效切断过越南的全部交通线，航空兵皮特·希拉里把轰炸效果描述为“将垃圾从路北边挪到了路南边。第二天，我们再把这点垃圾从路南边挪到路北边”。

式中：βk,1，βk,2为第k次谐波分量的系数。

根据式（9），光伏发电功率的超短期预测结果将由2 部分组成：（1）回归部分，主要来自SHSSRD和谐波分量的贡献；（2）残差部分，主要由ARIMA方法基于历史残差序列得到。

3 算例分析

3.1 实验设定

在算例分析中，本文采用第1 节介绍的数据集，验证时序动态回归模型的有效性，检验其在超短期光伏发电功率预测问题上的预测精度。从图3可以看出，每天从22：00 到次日5：00 这段时间内，光伏发电功率为0。因此，光伏发电功率的超短期预测将分时段进行：夜晚时段（20：00 到次日5：00共10 h）的预测结果直接取0；白天时段（6：00 到19：00 共14 h）利用式（9）所示的动态回归模型进行预测。因此仅对白天时段进行建模预测，故需要提前去除数据集内的夜晚时段数据，同时式（9）中谐波项的季节性周期设为m=14。

式（9）中待定参数可以分为2 类：（1）第一类包括回归参数β0，β1，βk,1，βk,2与ARIMA 公式中的系数φi，θi和常数项c等，它们被称为普通参数，可基于历史时间序列计算得到。其中，计算回归参数采用最小二乘估计，计算ARIMA 公式中的参数采用极大似然估计。在此过程中用到的历史时间序列长度被称为滑动窗口长度；（2）第二类参数包括滑动窗口长度，ARIMA 模型的阶数p，d，q及谐波分量的最高次数K，它们被称为超参数。本文通过时序交叉验证来确定超参数的最佳取值。

全体数据集被划分为训练集（前12 月，共5 110 h）和测试集（后3 月，共1 274 h）。时序交叉验证在训练集上进行，当确定普通参数和超参数的取值后，在测试集上检验模型的预测精度，评估指标统一采用均方根误差（Root Mean Square Error，RMSE），其量值为ERMS。

3.2 预测模型训练与测试

通过在训练集上执行时序交叉验证，可确定ARIMA 的最优阶数组合为（2，0，0），谐波分量最大次数为7，得到式（9）的具体形式，如式（10）所示。同时也确定滑动窗口长度为420 h（30 d）。

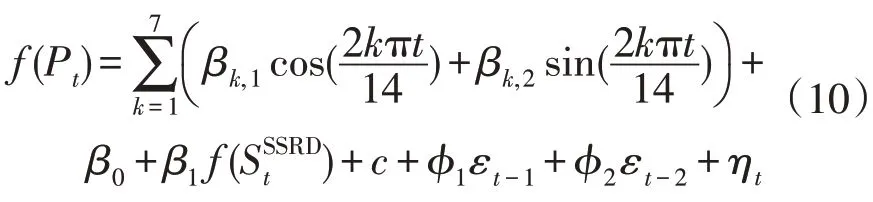
为展示式（10）中各分量对预测精度的贡献，设置3 个对照模型进行对比测试：（1）模型1，仅考虑SHSSRD 回归项，即采用式（2）所示的普通回归形式；（2）模型2，在模型1 的基础上，增加ARIMA 项，即式（7）所示模型；（3）模型3，在模型2 的基础上，增加谐波分量，即本文所提预测模型，如式（10）所示。

在测试集中随机选取1 d（2013 年6 月3 日），3个模型的超短期滚动预测结果（预测提前期为1 h）如图5 所示。

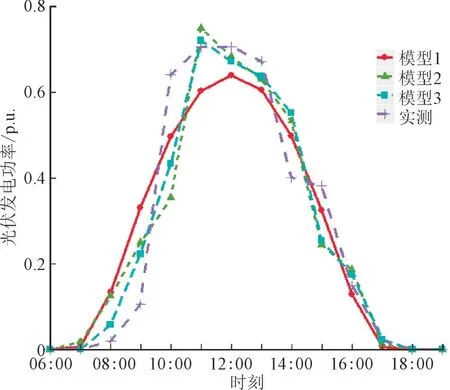
图5 3个模型的超短期滚动预测结果Fig.5 Very short-term rolling forecast results of three models

从图5 可看出，缺少ARIMA 项的模型1 预测效果明显比模型2、模型3 差；模型2、模型3 在下午时段的预测结果基本一致，在上午时段，引入谐波分量的模型3 预测效果相较模型2 有很大改进。表1 列出了3 个模型在测试集上超短期滚动预测的预测精度评估结果。

表1 3个模型在测试集上的超短期滚动预测RMSETable 1 Very short-term rolling forecast RMSE of three models on the test set

表1 数据表明，从模型1 到模型3，通过增加ARIMA 项和谐波分量，模型预测精度得到很大提高。此外，表1 还给出对数形式（式（3））动态回归模型的预测精度，虽然其总体预测效果要差于普通形式的动态回归模型，但通过分析每天各时刻的预测精度，发现对数形式在16：00 到次日6：00（忽略夜晚时段，见3.1 节实验设定）的预测精度明显高于普通形式。表2 列出了从16：00 到次日6：00 这一时段内，模型3 普通形式和对数形式的各时刻预测精度，包括训练集评估结果和测试集评估结果。

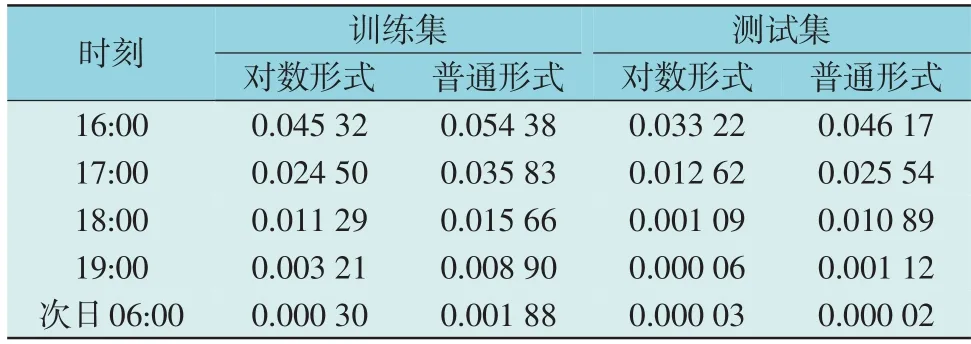
表2 模型3的对数形式与普通形式在16：00到次日6：00时段内的各时刻预测精度RMSETable 2 Forecast RMSE between logar-ithmic and normal forms of model 3 from 16：00 to 6：00

综合表1 和表2 展现的预测精度结果，本文采用一种混合预测方案，即在原实验设定下，进一步将白天时段划分为2 个时段：从7：00 到15：00 为第一时段，采用普通形式的动态回归模型进行预测；从16：00 到次日6：00 为第二时段，采用对数形式的动态回归模型进行预测。这种混合预测方案既保留普通形式模型优良的整体预测精度，同时也改善了在局部时段的预测精度。

3.3 与现有预测方法的对比分析

为检验第3.2 小节提出的混合预测方法的有效性，本文选择了3 种基于时间序列的光伏发电功率超短期预测模型作为对照组：（1）snaive 方法，即将前1 d 的同时刻实测数据作为预测结果；（2）STL+ETS 方法，是一种数据分解算法，可以分解得到光伏发电功率的日季节性分量，并以snaive 方法给出日季节性分量的预测结果[25]。去除日季节性分量的剩余部分则采用ETS（指数平滑）模型进行预测，ETS模型以历史数据的加权平均作为预测结果，权重系数按指数衰减；（3）STL+ARIMA 方法，其基本思路与STL+ETS 方法类似，不同点在于用ARIMA 模型取代ETS 模型，经交叉验证可得ARIMA 的最优阶数组合为（3，1，2）。

在测试集中随机选取2 d，2013 年5 月29 日为多云天，分别采用4 个模型进行超短期滚动预测（预测提前期为1h），其中2013 年5 月11 日为晴天的结果如图6 所示，2013 年5 月29 日为多云天的结果如图7 所示。

图6 4个模型在晴天的超短期滚动预测结果Fig.6 Very short-term rolling forecast results of four models on a sunny day

图7 4个模型在多云天的超短期滚动预测结果Fig.7 Very short-term rolling forecast results of the four models on a cloudy day

从图6 可看出，4 种模型在晴天的预测效果都很好，但是本文所提混合方法的整体预测精度明显要更高，尤其表现在上午光伏发电功率爬升时段。在图7 中，snaive 方法由于不能对天气变化做出响应，因此预测精度最差；而另外2 种对照方法的预测精度也不理想；总体上看，混合预测方法是4 种方法中跟随发电功率变化最准确、最快速的方法，因此其预测精度也最高。

表3 列出了4 种方法在测试集中的滚动预测精度评估结果。为使评价更全面，除RMSE 外，表3还给出了各方法预测值的平均绝对误差（Mean Absolute Error，MAE），其量值为EMA。表3 评估结果显示，在超短期预测精度上，基于动态回归模型的混合预测方法明显高于其他3 种对照方法。

表3 4种方法在测试集上的超短期滚动预测精度Table 3 Very short-term rolling prediction accuracy of four methods on the test set

为了检验所提方法对不同时间段的鲁棒性，将3 个月测试集数据（2013 年4—6 月）按时间先后分为6 部分（每半月构成一部分），分别统计4 个模型在6 个时段滚动预测误差（只包括预测提前期为1 h 的预测）的RMSE 值，得到结果如图8 所示。

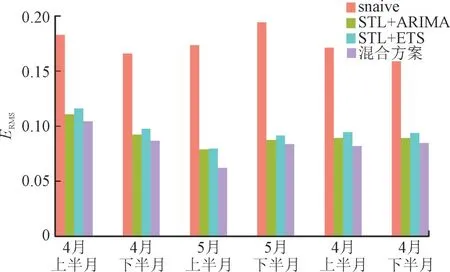
图8 4种方法测试集超短期滚动预测的分时段RMSE统计结果Fig.8 Time-segmented RMSEs of very short-term rolling forecasting of four methods on the test set

从图8 可看出，在4 种预测方法中，所提混合方案在6 个时间段内的预测效果均为最佳，且在不同时段内的预测精度差别不大，说明所提方法具有一定的时间鲁棒性。

4 结语

本文提出的基于动态回归的超短期光伏发电功率预测方法，仅需要历史光伏发电功率数据与数值天气预报作为输入即可实现较高精度的预测。算例结果表明了与单一的普通形式回归模型相比，综合了普通形式回归模型与对数形式回归模型的混合预测方法具有更好的预测效果。算例也验证了相较于一般的时序模型，本文所提出的预测方法在超短期光伏发电功率预测方面预测精度更高。