基于主从博弈的共享储能分时电价策略

2022-07-26张青苗陈来军马恒瑞薛小代梅生伟

智慧电力 2022年7期

张青苗，陈来军，马恒瑞，薛小代，2，梅生伟，2

（1.青海省清洁能源高效利用重点实验室（青海大学新能源光伏产业研究中心），青海西宁 810016；2.电力系统及发电设备控制和仿真国家重点实验室（清华大学电机系），北京 100084）

0 引言

由于用电需求的日益增长，供电负载峰谷差也在不断变大[1]，而储能系统不仅可以平滑负荷峰谷，降低对电网的冲击和压力，还可对可再生能源发电系统供电进行调节，提高供用电的可靠性和利用率[2-3]。由于储能系统的投资成本高，需较大的投资规模，且回报周期也相对较长，限制了用户对储能系统的投资建设，同时由于储能产业的商业化模式尚未明确，进一步限制了储能系统的发展。2021 年7 月，国家发改委、国家能源局共同发布《关于加快推动新型储能发展的指导意见》，要求强化规划引导，鼓励储能多元发展。积极推进源、网、荷侧储能多元化发展为了使这些问题得到有效解决，青海省在全国首创性地提出了“共享储能”模式[4-5]。“共享储能”以储能容量租赁、虚拟电厂调度优化和社区储能资源分配等方式，在提高储能系统利用率的基础上，增加了总体收益[6-7]。随着“共享储能”的普及和推广，探索储能在使用需求上的互补性和合理的价格机制，提高储能资源的充分利用及各主体的收益，同时减少用户用电成本及电网压力，逐渐成为近年来的研究热点。

近年来，国内外对共享储能在各方面展开了大量研究。文献[8]提出基于发电侧储能供需的形成、匹配和收益分配机制，在合作博弈基础上，建立了共享储能规划模型，通过实际数据仿真检验了共享储能机制和博弈模型的有效性。文献[9]对用户独立储能和社区共享储能进行研究分析，验证了社区共享储能具有更高的储能利用率和更大的容量需求。文献[10]提出一种储能与多种常规调峰手段优化组合调峰方案，建立了其参与电力市场的经济性评估模型。文献[11]基于时间尺度构建多能量市场购电模型和差异化合同售电模型，通过条件风险价值评估损失和收益，并确定购售电策略。文献[12]建立了用户侧储能多维度方面的互动机制，对比分析不同电网交互模式的风险和特性，验证了合理的商业模式和运营策略可提高储能的盈利水平，实现各主体的协同共赢。文献[13]研究了社区综合能源系统，建立多能源协同优化调度模型，对用户每日能源消耗量进行分配和优化，从而减少其用能费用的支出。

关于共享储能的研究较少考虑在价格信号引导和刺激下，用户根据自身需要调整用电方式产生的影响，对用户使用共享储能的充放电行为和用户与共享储能间互动分析较少。因此本文提出在共享储能中引入“需求侧管理技术”[14-17]，借助需求响应来解决这些问题。通过储能系统，将用电高峰期的部分负荷转移到电价较低时使用，不仅能达到削峰填谷、提高储能收益的目的，同时也能为用户节省用电成本[18]。

主从博弈适用于分析过程复杂的序贯决策问题[19-21]，目前已被广泛应用于价格制定相关研究中。本文提出一种基于主从博弈的共享储能分时电价策略，所提策略以分时电价为研究基础，以主从博弈方法为工具，以共享储能为研究架构，对分时电价的最优策略进行分析。

1 社区共享储能电站运营模式分析

1.1 居民社区共享储能电站运营模式

随着社区用户日益增长的用电需求，考虑到用电峰谷时段的负荷状态及电价差异，为降低社区用户用电成本，在社区内部建立共享储能电站，使得多个用户可以享受共享储能服务。居民社区共享储能电站总体运营模式如图1 所示。

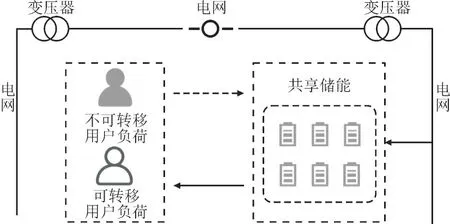
图1 居民社区共享储能电站总体运营模式Fig.1 Overall operation mode of residential community shared energy storage power station

居民社区共享储能电站总体运营步骤如下：

1）储能电站收集用户历史用电情况及未来各时段负荷用电预测信息等，通过匹配、优化制定分时电价。

2）社区用户通过对比电网和储能电站的价格进行选择。在电网电价较低时段，使用电网满足日常用电需求，同时共享储能电站选择在该时段进行充电。

3）在电网电价较高时段或用电高峰时段，共享储能进行放电，用户优先选择使用共享储能满足用电需求。同时，用户可根据储能电站提供的分时电价高低选择在该时段满充或仅满足最小用电负荷。

该模式中由于用电时段的负荷能否转移会直接影响用户各时段的用电功率和成本，故本文将用户负荷分为可转移负荷和不可转移负荷[22-24]。对于可转移负荷，如洗衣机和热水器等，在用电高峰（电价较高）时段，用户可选择对非必要负荷进行转移，在其他时段继续使用；而不可转移负荷，如居民的夜间照明和冰箱等，只能在一定程度上削减其负荷且要保证用户日常生活不受影响。

基于居民社区共享储能电站的应用场景，共享储能电站运营商需要制定各时段的电价，且其收入取决于用户各时段的用电功率，而用户各时段用电功率的决定权并非在于储能运营商，主要受到储能电站运营商给出的分时电价的影响。由于共享储能的电价还会受到电网电价的影响，若某时段电价高于电网电价，用户则会选择从电网购电，若某时段电价低于电网电价且储能设备存储有充足的电量，用户则会优先选择从共享储能购电，故而构成主从博弈关系。

1.2 共享储能-用户互动分析

在本文中，共享储能根据用户用电功率情况制定各时段的电价，在一定程度上提升用户用电高峰时期的电价，使储能收益最大化。而用户根据共享储能各时段的电价决定各时段的用电功率，在电价较高时段，用户可选择减少在该时段的用电功率，将该时段的可转移功率转移至电价较低时段使用，使得用户成本最小化。

这种共享储能用户的互动情况符合主从博弈模型架构。该博弈将共享储能和社区用户作为参与者，共享储能电站和社区用户的策略分别为分时电价和用电功率，支付分别为储能收益和用户成本。共享储能先做出决策，用户作为跟随者根据共享储能的策略做出对自己最有利的决策，然后博弈主导者再根据跟随者的策略优化自己的决策，两者相互影响，直至实现均衡。

2 社区共享储能电站主从博弈模型建模

2.1 储能电站博弈模型

作为主从博弈的主导者，储能电站参考用户的历史用电情况优先制定决策，决定分时电价，使收益最大。总收益Fs由向用户售电的收入、从电网购电的成本以及储能的投资Rini和运维成本Rop组成，可表示为：

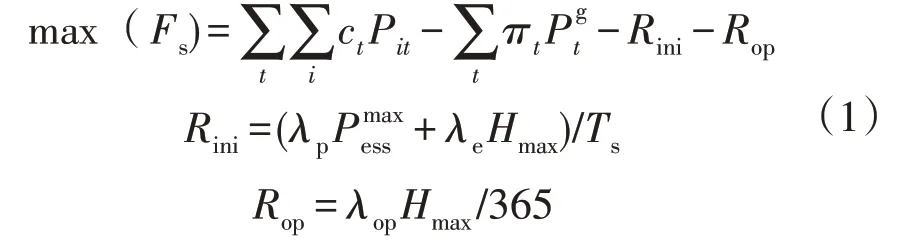
式中：ct为t时段的充电价格；Pit为t时段第i个用户的充电功率；πt为t时段共享储能的购电电价；为t时段的购电功率；λp和λe分别为储能设备的功率成本和容量成本；和Hmax分别为储能设备的最大充放电功率和最大容量；Ts为储能设备的预期寿命周期；λop为储能设备单位容量年运行维护成本。

储能电站模型约束具体如下。

1）储能电价约束：

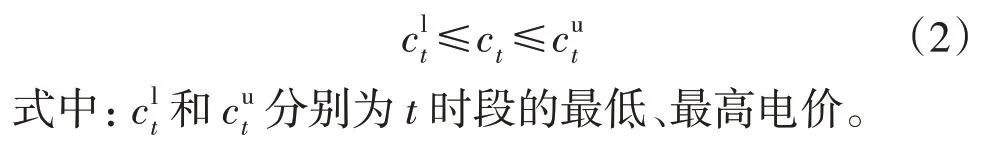
2）功率平衡约束：

3）储能设备充放电功率约束：

4）储能设备的荷电状态约束：

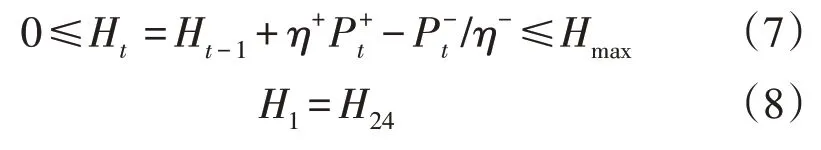
式中：η+和η-分别为储能设备的充、放电效率；H1为使用前储能设备的初始电量；H24为最后时刻储能设备的荷电量；Ht和Ht-1分别为t时段和t-1 时段储能设备的电量。

储能设备在各个工作周期（本文将全天划分为24 个时段）内的充放电量累计值应为0，从而保证储能电站稳定高效的运行。

2.2 用户侧博弈模型

用户作为主从博弈的跟随者，目标为最小化自身用电成本Fg，其由用户从共享储能购电费用和从电网购电费用组成，可表示为：

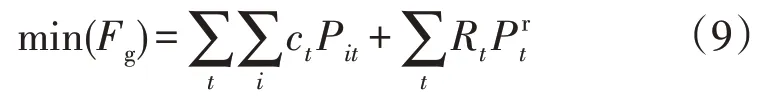
式中：Rt为t时段用户从电网购电的电价；为t时段用户从电网购电的功率。

用户侧模型约束具体如下。

1）用户侧充电功率约束：

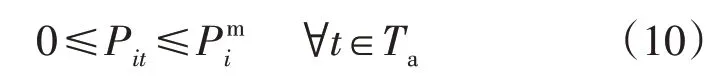
式中：Ta为用户的用电时间段；为第i个用户的最大充电功率。

2）用户总功率约束：

3 博弈问题分析与求解

3.1 双层规划建模

双层规划模型可用来描述该主从博弈问题。上层模型以共享储能分时电价为决策变量，以储能总收益最大为目标；下层模型将用户提供的用电功率作为决策变量，以用户用电成本最小为目标，上下层都有不同的约束条件。图2 是双层规划结构图，其中上层共享储能模型将下层社区用户模型作为约束条件，下层模型以上层模型的解为优化变量，上下层之间相互约束，彼此制约。

图2 双层规划结构图Fig.2 Double-layer planning structure diagram

3.2 非线性规划转化

在主从博弈中，用户基于既定的电价进行用电量的决策，可用Karush-Kuhn-Tucher（KKT）互补松弛条件将下层模型转换为上层模型的约束条件，求出变量{ct} 和{Pit} 的约束关系，解决该优化问题。将对偶变量分别记为和{ }μit，则线性规划式（9）—式（11）的KKT 条件为

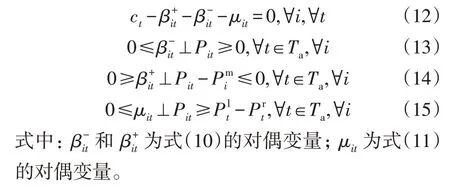
通过式（12）—式（15）处理，储能电站的目标函数式（1）和互补松弛条件式（13）—式（15）是非线性的。

3.3 互补松弛条件的线性化

将3.2 节中互补松弛条件下的非线性问题进行线性化，利用Big-M 法，通过引入布尔变量和δit将约束式（13）—式（15）转化为以下线性不等式：

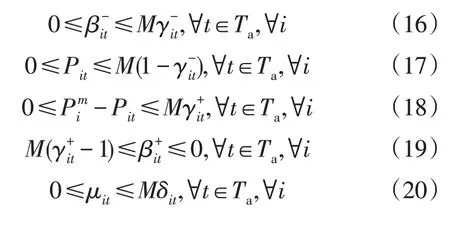
3.4 目标函数的线性化

在3.2 节和3.3 节一系列转化的基础上，还需采用布尔展开法对目标函数进行线性化，以消除电价和充电功率相乘形成的双线性项ct Pit。将用户各时段的用电功率Pit进行离散化处理，可表示为：

在此基础上，引入新约束如下：

通过对复杂的双层优化问题进行转化和处理，可将其变为混合整数二次规划问题并直接求解。

4 算例分析

4.1 系统配置

本文用电侧的主体为社区居民。算例中储能容量固定，提供给用户零售电价下限=0.8 πt，上限=1.2 πt，储能设备的功率成本和容量成本分别为800 元/kW 和400 元/kWh，储能年运行维护成本为30 元/kWh。储能设备的参数见表1[25]。

表1 储能设备参数Table 1 Energy storage equipment parameters

4.2 结果分析

运用Matlab 建模并调用CPLEX 优化软件对模型进行求解，得到共享储能的最大日收益为530.85元。共享储能的最优电价策略如表2 所示。

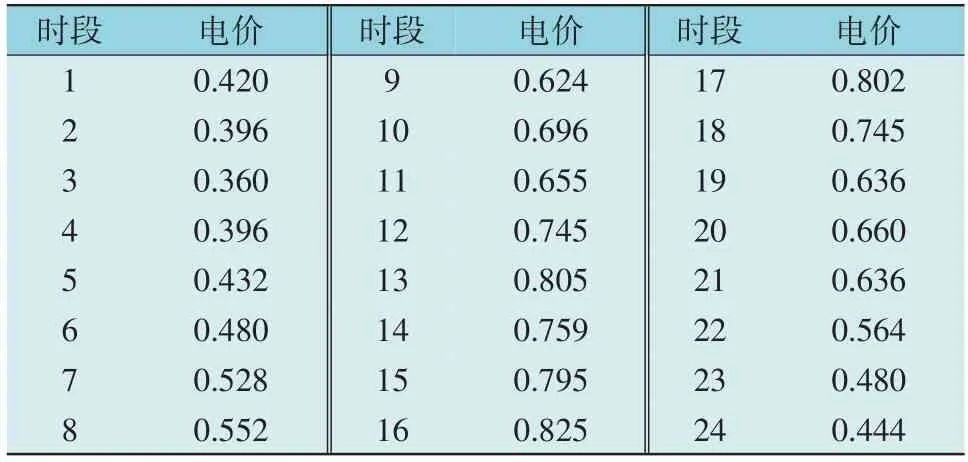
表2 共享储能最优电价Table 2 Optimum electricity price of shared energy storage 元·（kWh）-1

社区用户根据分时电价策略，在各时段选择满充或仅满足不可转移负荷，给出的最优用电功率如图3 所示。

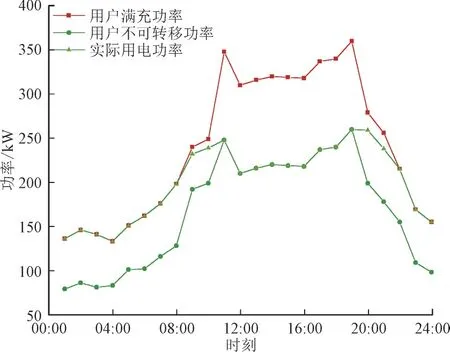
图3 用户实际用电功率图Fig.3 Actual user power consumption diagram

由表2 和图3 可以看出，在以共享储能收益最大和社区用户成本最小为背景下，该分时电价的制定策略仍能起到削峰填谷的作用。共享储能在20：00—24：00 和01：00—10：00 电价较低时段，提高其售电价格，倾向于选择充电，此时其售电价格高于电网零售价格，故用户在该时段选择使用电网满足自身用电需求，且由于该时段是电价较低时段，用户选择满充满足用电负荷；而在11：00—19：00 电价较高时段，共享储能倾向于放电以“低充高放”获得更多的收益，为了吸引用户改变购电渠道，故其选择以低于电网零售价格进行售电，此时由于共享储能提供的电价较低，为降低自身用电成本，用户优先选择使用共享储能满足该时段最小用电负荷。

储能系统荷电状态（State of Charge，SOC）各时段的状态如图4 所示。由图4 可以看出，储能系统的充电时间集中在夜间时段，在01：00—03：00 时段，电网的电价较低，储能设备以最大充电功率进行充电，直至达到系统的存储上限；而11：00—19：00时段为用户的用电高峰时段，且电网的电价比较高，故储能设备在该时段内进行放电。由此可知，共享储能的购售电策略符合常理。

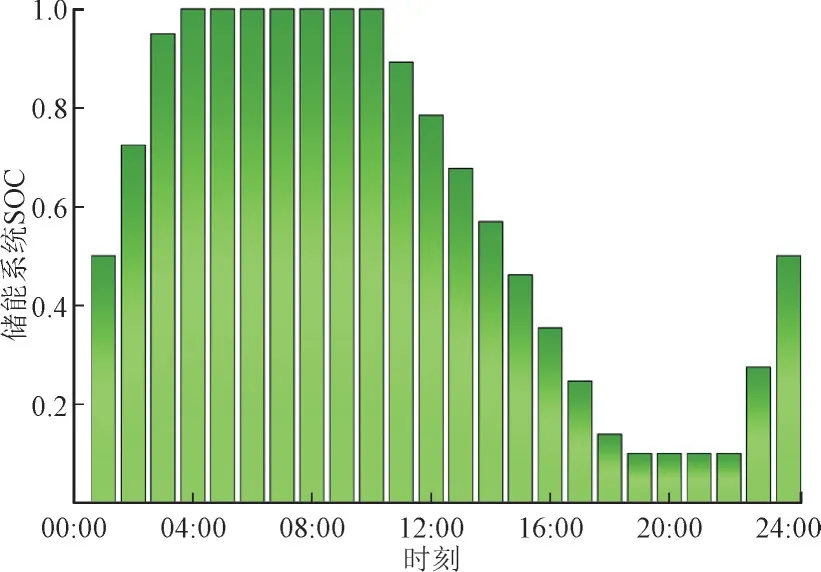
图4 储能系统SOC状态图Fig.4 SOC status diagram of energy storage system

接下来对有无博弈的用户成本进行分析，分析结果对比如表3 所示。

表3 有无博弈用户成本对比Table 3 Comparison of user costs with or without gaming

由表3 可以看出，用户在参与主从博弈策略时，其用电成本较未参与博弈时有所减少。由此可知，基于主从博弈的共享储能分时电价策略，在增加储能收益的同时也能减少用户用电成本。

4.3 不可转移负荷比例影响分析

在保证其他参数不变前提下，改变不可转移最小负荷，不可转移最小负荷在0.1 倍到0.9 倍间变化，用户从共享储能购电量和从电网购电量的变化如图5 所示。

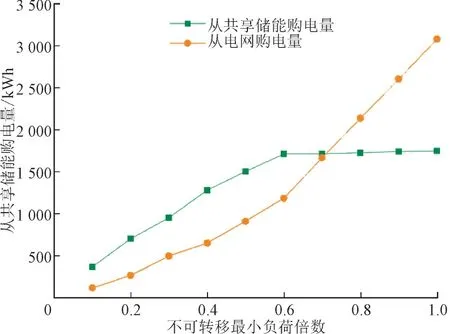
图5 不同不可转移负荷下用户购电量对比Fig.5 Comparison of user power purchases under different non-transferable loads

由图5 可知，随着用户不可转移负荷的增加，用户从共享储能和电网的购电量也都在增加，且电网的购电量相较于共享储能有明显的增加。这是因为随着不可转移最小负荷的增加，各时段可转移功率减少，故用户在各时段从共享储能和电网的购电量都有所增加，同时用户在电网电价较高时段选择转移到电价较低时段时使用共享储能的功率相对减少，用户从电网的购电量有更快的增速，从而导致用户的用电成本增加，共享储能此时的收益也有所增加。为了兼顾共享储能和用户两者的利益，不可转移的最小负荷应综合考虑选取适当值。

4.4 共享储能容量影响分析

假设共享储能容量从1 MWh 到2 MWh 变化，保持其余参数不变，共享储能各时段的电价变化如图6 所示。

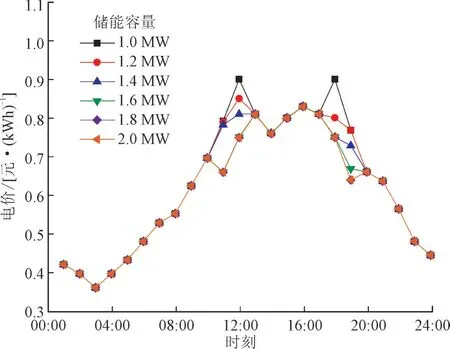
图6 不同储能容量下共享储能分时电价Fig.6 Comparison of time-sharing electricity price of shared energy storage under different capacity

由图6 可知，随着共享储能容量的增加，储能用电高峰时段的电价先下降，而后保持不变。因为储能的容量增加，使其可以在低电价时段购进更多电量进行储存，使储能的购电成本有所下降。同时，在高电价时段，储能可提供给用户的总电量有所增加，为了提高储能收益，使得更多用户选择使用该设备，在储能容量增加的同时，相对减少用电高峰时段的电价。由于受到共享储能的充放电速率和用户负荷需求的限制，随着储能设备容量的增加，其边际收益是逐步变小的。当边际收益趋于0后，共享储能的利润将达到峰值并保持不变。因此在设置储能容量时，需要从需求出发，合理设置边际成本（即储能容量配置）以实现利润的最大化。