振型分解法教学中柔度影响系数的应用
2022-07-25孙旭峰
孙旭峰
(扬州大学建筑科学与工程学院,江苏 扬州 225127)
在结构力学的动力学一章中,振型分解法(或振型叠加法)是求解任意动力荷载作用下线性体系响应的一种基本方法,其基本思路是利用结构主振型之间关于质量矩阵和刚度矩阵的正交关系,将具有n个振动自由度的动力方程组解耦,从而基于主振型的正则坐标线性组合求解结构响应[1][2]。
但在振型分解法中,仅假设动力荷载作用于质点的振动自由度方向,而对于存在非质点及非自由度方向动力荷载作用的求解(如图1所示)则鲜有涉及。
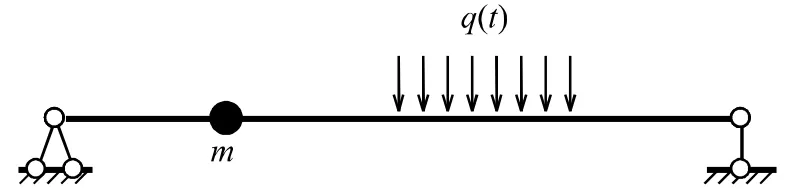
图1 动力荷载不作用于振动自由度方向的情形
文献[3]通过算例指出,如果将动力荷载作用的无质点位置计入振动自由度参与计算,则该自由度方向由振型分解法求得的位移结果是不正确的,其原因是零质量导致了无穷大的频率分量。
事实上对于此类问题,在振型分解法中引入柔度影响系数的概念即可解决。
1 引入柔度系数影响矩阵后的振型分解法
由结构力学中的柔度法可知,当不计阻尼的影响时,n个振动自由度结构在任意动力荷载作用下的振动微分方程为



由式(4)可知,在引入柔度影响系数后,只需将传统振型分解法方程的右端项左乘即可。若所有激振力均作用于质点的振动自由度方向,则,此时即退化为传统振型分解法的情形。
引入柔度影响系数矩阵后,振型分解法的求解步骤如下:
(2)计算广义质量和广义荷载

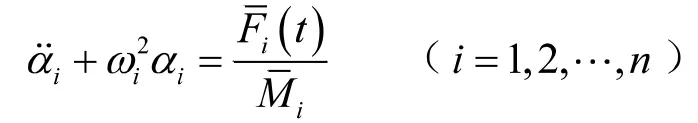
(4)计算几何坐标(质点位移)
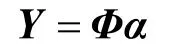
2 算例
图2所示结构在12杆及结点2处分别受到突加均布荷载及突加集中力偶作用
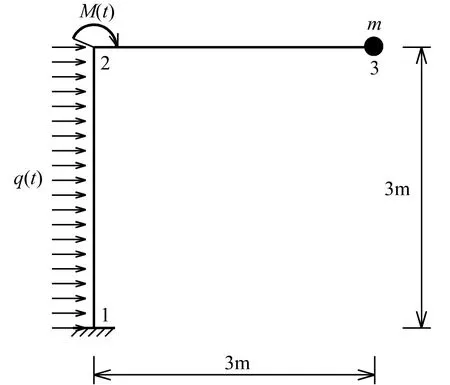
图2 算例
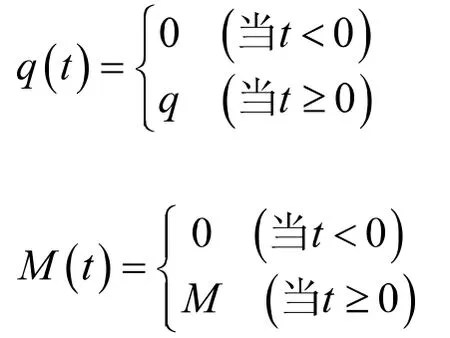
试求质点m的位移响应,设杆件的抗弯刚度EI为常数,不计杆件的质量及轴向变形。
对于该算例,若不计质点的转动惯量,则可知质点m存在水平和竖直两个方向的振动自由度y1和y2,而突加均布荷载及突加集中力偶均不作用于质点的振动自由度方向。若令,则由图 3(a)、(b)的弯矩图与图4(a)、(b)的弯矩图分别图乘,即可求得柔度影响系数矩阵为
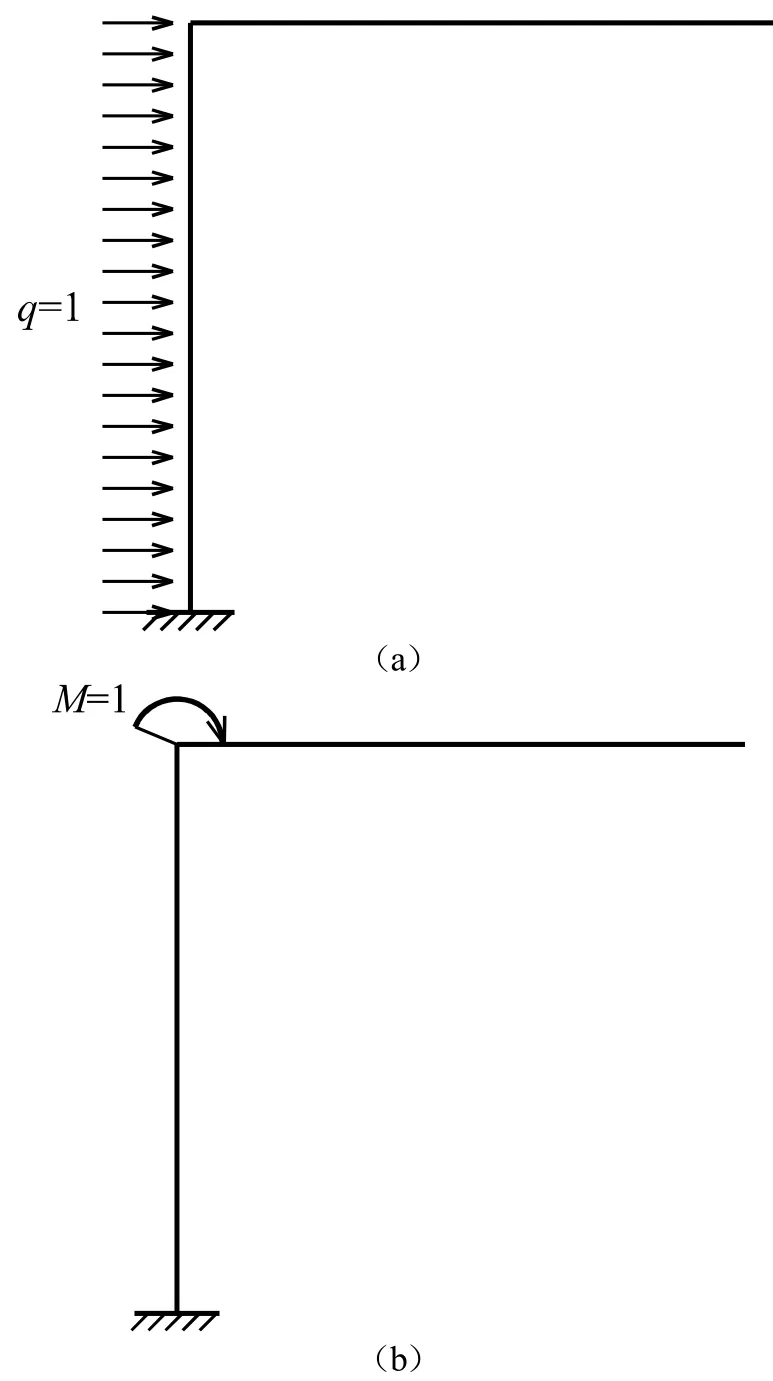
图3 单位激振力
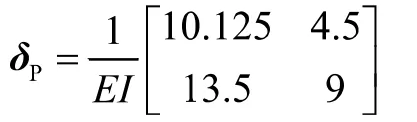
而由图4(a)、(b)的弯矩图图乘可求得结构的柔度矩阵为
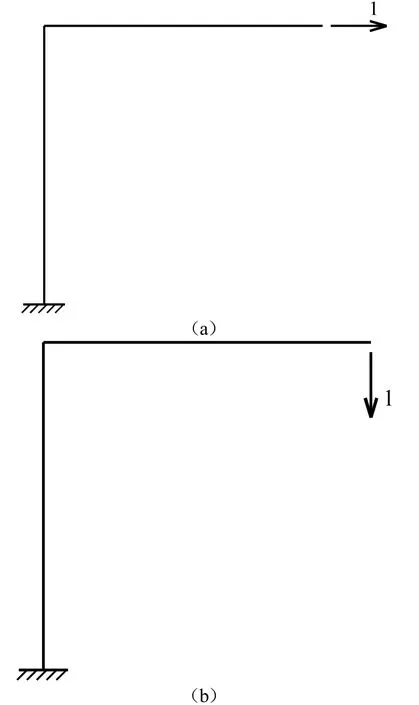
图4 振动自由度方向的单位力

其逆矩阵即为结构的刚度矩阵
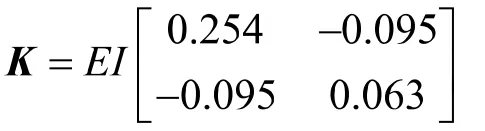
利用柔度法或刚度法可求得结构的自振频率及主振型分别为
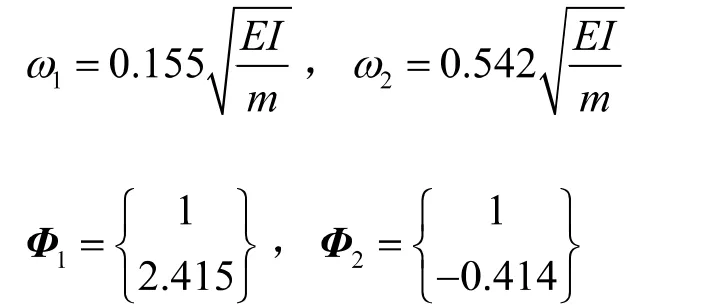
因此,该结构的广义质量和广义荷载分别为
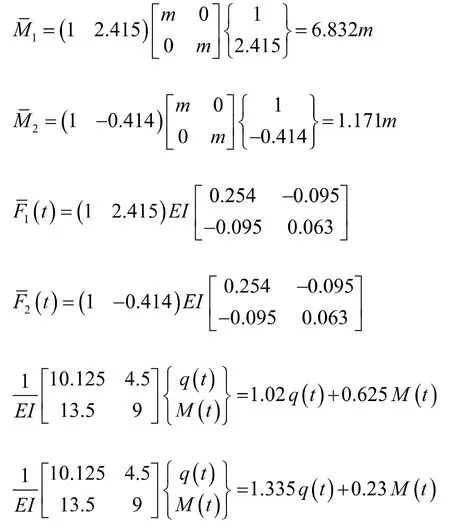
利用杜哈梅积分求解正则坐标的振动微分方程,可得

最终,可求得两个振动自由度方向的位移解为
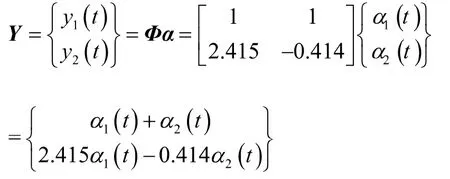
3 总结
振型分解法(或振型叠加法)可用于求解线性体系在任意荷载作用下的响应,但是在用刚度法推导其基本方程时,一般都是假设动力荷载作用于质点的振动自由度方向,而对于存在非自由度方向荷载,特别是分布动力荷载的情形则鲜有论述。
针对这一问题,本文基于柔度法,利用柔度影响系数的概念对振型分解法进行了修正,该方法只需在传统振型分解法方程的右端项左乘即可,而其求解过程与传统振型分解法基本一致。算例表明,经修正后振型分解法即可用于存在任意非质点非振动自由度方向荷载情形的精确计算。
