基于自编码LCD棋盘格的数码相机标定方法
2022-07-25李嘉欣张芳菲赵紫为
李嘉欣,张芳菲,赵紫为
(1.渤海大学 信息科学与技术学院,辽宁 锦州121013;2.中电太极(集团)有限公司,北京100083)
0 引言
随着计算机视觉、数字摄影测量理论的发展,各类摄像机经严格标定后,已经用于三维重构、视觉测量、机器人导航、遥感测绘等领域[1-27].基于靶标的摄像机标定是广泛应用的标定方法,与三维靶标相比,平面靶标制作简单,研究者们通常使用棋盘格、圆形、星点、格网等构成的二维标定场进行摄像机标定.摄像机标定旨在通过建立标志场图像坐标系和空间坐标系的变换关系,求解相机的内参、外参以及畸变系数.因此,摄像机标定精度很大程度取决于标定板的精度,大量标志点识别的自动化程度决定了摄像机标定的效率.
张正友提出的棋盘格相机标定法[11],标定精度可以满足普通相机的需求,且可以实现标定过程的自动化,但对于标定板的平面度要求较高,其制作成本较高.Opencv[12]提供了角点排序的方法,但在摄像机偏转角度大或者棋盘格的长宽数目相同的情况下,获得的影像角点排序是混乱的,降低了标定的效率.赵斌等[13]人提出了一种改进棋盘的角点自动检测与排序方法,确定角点原点和长、短轴,并通过距离对角点进行排序,具有旋转不变性,但该方法仅适用于畸变较小的图像.张维忠等[14]人提出了一种绕光轴旋转拍摄LCD上平面靶标的方式进行相机标定,利用LCD屏具有可视角度和极高平面等特性,通过较少图像即可得到较高的标定精度,但对于角点排序没有涉及.因此设计出一种低成本、高精度的标定板与排序算法是相机标定的关键.
LCD[1-5]具有较高的纯平面性和几何精度,其成本较低,所以本文设计了一种附有编码标志的LCD平面棋盘格,建立了棋盘格角点自动编码方法,以实现其像点与物点编号的自动对应;最后,基于该平面棋盘格实现了摄像机的自动高精度标定.
1 相机标定模型
假设空间中存在一点P,其对应像点为p;P的物方坐标为(xw,yw,zw),对于平面标定板,zw=0;p的像素坐标为p(u,v),则P点的物方空间坐标与其像平面的像素坐标的转换关系如式(1)所示:
(1)
其中:zF为比例因子;B1为内参数矩阵,如式(2)所示:
(2)
其中:f为焦距;dx、dy为像素的物理尺寸;(u0,v0)为图像主点坐标.B2为外参数矩阵,如式(3)所示:
(3)
其中:R代表旋转矩阵;T代表平移向量;Xw为物方齐次坐标向量,Xw=[xwywzw1]T,B为投影矩阵.
然而,相机的透镜加工、组装过程等产生的误差会带来不同程度的系统畸变,主要包括径向畸变和切向畸变,模型分别如式(4)、式(5)所示:
(4)
(5)
进而求得校正后的像点:
(6)
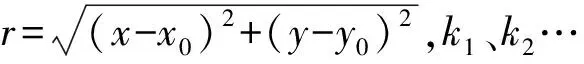
OpenCV库中的标定算法采用的是张氏标定法,即利用平面棋盘格作为标定板,标定摄像机内外参数和径向、切向畸变参数.
本文以LCD平面棋盘格替代精密棋盘格对摄像机进行标定.为求解最优参数,建立重投影误差为最小的目标函数,如式(7)所示.将式(1)求解的理想情况下的内参、外参以及利用最小二乘法求解的畸变系数作为初始值,通过Levenberg-Marquardt迭代算法使其最小化,优化求解相机内、外参数和畸变参数.
(7)
式中,n为拍摄的标定板图像数目,m为每张图像的角点数目,hij为第i幅图像第j个角点的实际坐标,Q为重投影方程,D为镜头畸变参数,Ri为第i幅图像从世界坐标系到相机坐标系的旋转矩阵,Ti为第i幅图像从世界坐标系到相机坐标系的平移向量,Sj为第j个角点的物方坐标.
2 基于LCD的棋盘格靶标设计与自动编码
传统的标定方法需要利用平面标定板等特定标定物,需要较高精度的加工工艺进行加工,若标定板平面度的误差达到1%时,都会导致较高的标定误差,而制作高精度的标定板非常困难并且成本较高.目前,LCD的使用越来越广泛,其制造工艺可以达到较高的几何精度,其平面度已经达到工业级水平.因此,本文设计一种显示于LCD上的棋盘格靶标.首先,根据LCD屏幕尺寸与分辨率,生成单元棋盘格边长为14.34 mm的棋盘格靶标;其次,为了实现自动编码,设计由三个红色圆组成的编码定位标志,如图1(a)~(b)所示.最后,根据设计的靶标,提取棋盘格特征点,并实现自动编码,用于摄像机标定.

图1 (a)附有标志圆的LCD 平面棋盘格标定板ꎻ(b)附有标志圆的LCD 平面棋盘格标定板(编码)
2.1 棋盘格角点的高精度提取
Harris角点检测[26]是常用的角点检测方法,其算子具有旋转不变性、尺度不变性等优点.令图像I以点(x,y)为中心的窗口为w(x,y),(u,v)为该窗口内的点,I(u,v)为其灰度值;将该图像窗口平移,使其中心平移至(u+Δx,v+Δy),I(u+Δx,v+Δy)为其灰度,将该窗口灰度的整体变化设为c(Δx,Δy),如式(8)所示:
(8)
其中,
ΔI(Δx,Δy)=I(u,v)-I(u+Δx,v+Δy)
(9)
根据邻域灰度连续性,如式(10)所示:
I(u+Δx,v+Δy)=I(u,v)+Ix(u,v)Δx+Iy(u,v)Δy+O(Δx2,Δy2)
(10)
其中,Ix,Iy是I(x,y)的偏导数,也就是图像在x和y方向的梯度;将式(10)带入式(8),对于局部微小的移动量(Δx,Δy),可近似为:
(11)
其中,
(12)
Harris角点响应函数则定义为:
R=detM-α(traceM)2
(13)
其中,detM=λ1λ2是M的行列式,traceM=λ1+λ2是M的迹,λ1、λ2是M的特征值,α是经验常数,R>t检测出的是角点,t为设定的阈值.显然,Harris角点检测的稳定性和α值有关,α不容易取得最佳值.
Shi-Tomasi角点检测算法[27]是对Harris角点检测算法的改进,该算法将角点响应函数即式(13)改进为R=min(λ1,λ2),若该函数大于设定的阈值,则该点是角点.
以上述Shi-Tomasi法检测的棋盘角点(对应像素级精度的角点)为初值,检测亚像素角点坐标,其原理如下[12]:
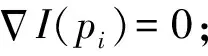
(14)
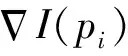
(15)
求解角点的亚像素精确位置即可转换成求解误差和S最小的问题.可通过迭代法求解得到亚像素点最优解.
2.2 棋盘格角点自动编码算法
为了实现相机的自动标定,本文提出了一种棋盘格角点自动编码方法,即通过自动识别3个红色定位圆对影像区域进行分割,从而对提取的每个棋盘格角点进行自动编码,实现角点和物方点编号的自动匹配.如图2所示,自动编码的原理如下:

图2 棋盘格角点自动编码流程图


(16)


5)分别计算V_left_up、V_right_up、V_left_down三个集合内的点P到O1的距离:
(17)
分别找到三个集合中距离O1最远的点A0(xa0,ya0)、A22(xa22,ya22)、M0(xm0,ym0),即确定棋盘格的左上角点、右上角点和左下角点;
6)将棋盘格的左上角点,即A0,存入行角点集合rowi(i=1,2,…,r)中,同时,将其存入起始点角点集合origin_node中,将A0从总集合V中剔除;

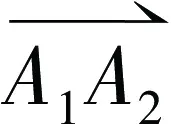
9)以row_head[0],即B0为起始点进行搜索,循环执行步骤6)7)8),直至排完第r-1行,停止执行;
10)将上述排完序的r-1行角点剔除后,剩余点即为第r行角点,计算角点距lA0M0的距离d,按照距离升序排序,并存入rowr中,排序结束.
3 实验分析
分别利用精密棋盘标定板和本文所述LCD棋盘标定板,结合OpenCV开源标定库函数,标定一款小蚁运动相机的内参、外参和畸变系数.
首先,准备好两个标定物,其一为精度达到0.01 mm的高精度棋盘格标定板,正方形小格边长为 12 mm;其二为显示在LCD液晶显示器上的棋盘格,正方形小格的边长为14.34 mm.将以高精度棋盘格为靶标的传统标定法作为方法A,将本文所述的基于LCD棋盘格标定法作为方法B.为评定两种方法的标定精度,分别以方法A、B进行标定实验,从不同角度和距离对精密棋盘格和LCD棋盘格分别摄取 24张影像,如图3~4所示,方法A选取均匀分布的224个特征点用于标定,48个特征点作为检查点;方法B选取均匀分布的260个特征点用于标定,39个特征点作为检查点(为避免检测特征点检测粗差对标定的影响,两种方法均采用Levenberg-Marquardt迭代计算逐步剔除粗差的方法),标定结果如表1所示.利用实验求解的摄像机内、外参数和畸变参数,计算各影像检查点的反投影均方根误差.如表2所示,方法A中,x轴方向的均方根误差dx_RMSE的平均值为0.544pixel,y方向的均方根误差 dy_RMSE的平均值为0.491pixel;方法B中,x轴方向均方根误差dx_RMSE的平均值为 0.569pixel,y方向的均方根误差dy_RMSE的平均值为0.543pixel,不考虑粗差的影响,方法B的标定精度与方法A相近.
此外,本文设计的标定板具有旋转不变性,如图4(a)~(d)所示,对于0~360度内旋转拍摄出的有畸变影像,本文提出的编码算法都可以唯一确定棋盘格角点的编号,有利于实现摄像机标定的自动化.

表1 标定结果
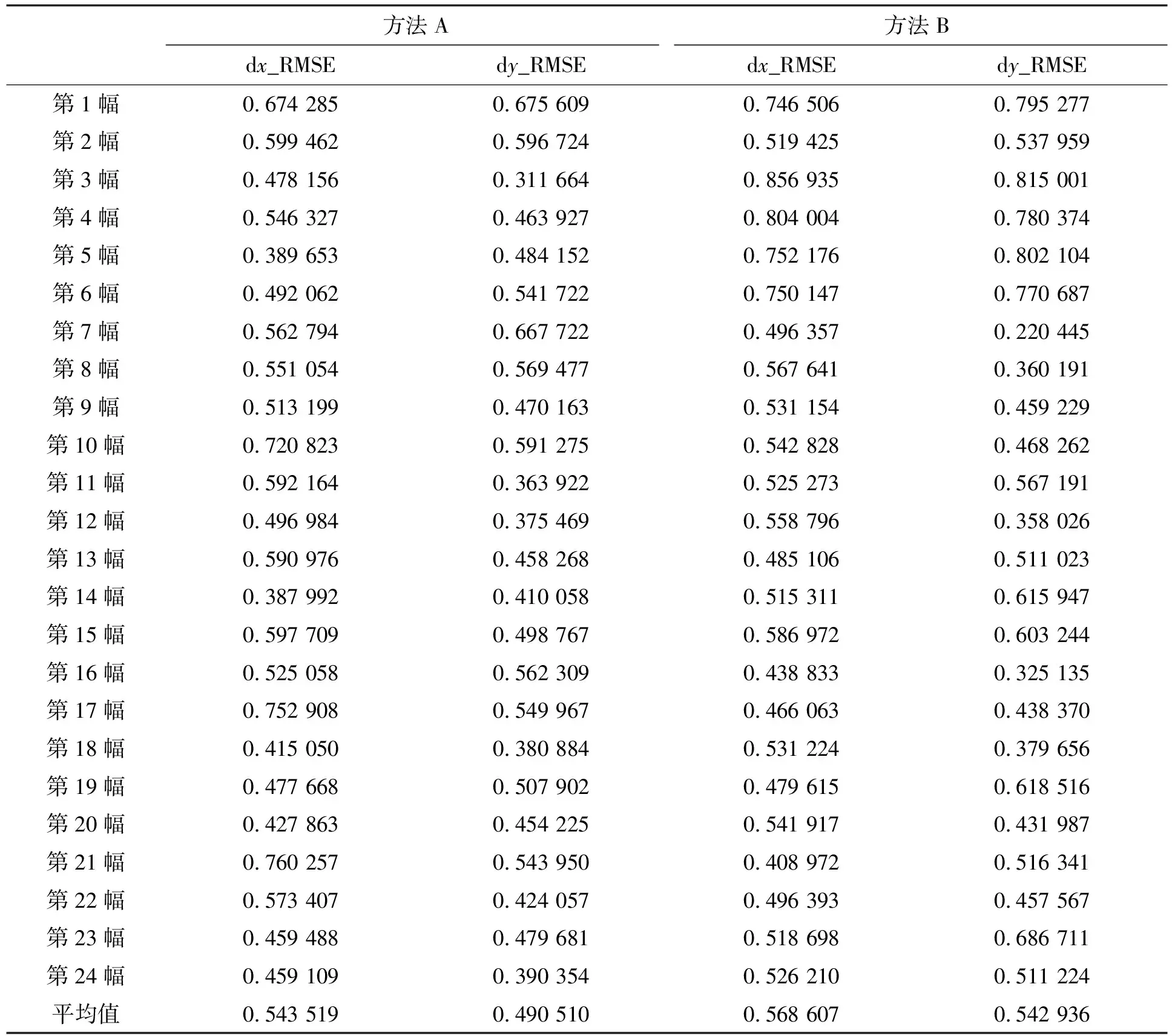
表2 标定精度

图3 精密棋盘格标定影像(部分)

图4 LCD棋盘格标定影像与角点编码(部分)
4 结论
传统棋盘格模板制作成本较高,制作工艺较复杂,LCD具有较高的纯平面性和几何精度,所以本文将棋盘格显示在LCD上作为摄像机标定的靶标,并在其附上三个定位圆,提出了一种适用于大畸变、大旋转影像的编码方法.实验表明,以LCD棋盘格为模板标定摄像机的精度接近于以精密棋盘格为模板的标定精度,精度较高;提出的棋盘格角点编码方法简单、实用且具有旋转不变性、鲁棒性强.
