基于连续图像消影点的视觉定位算法研究*

王 媛，刘小晗，王文杉，许忠雄

（中国电子科学研究院，北京 100041）

0 引言

移动智能终端的发展使其成为导航定位的研究对象，内置的卫星信号接收模块、摄像头和各种惯性传感器等硬件提供定位所需信息。一些学者发现，视觉传感器获得的图像可以用于定位，通过视觉设备获取场景信息，通过图像分析、目标识别等技术，计算载体局部相对位姿。图像能够提供丰富、准确、直观的环境信息，符合人的视觉观察习惯且易于理解，图像辅助智能终端定位价格低廉、使用方便，可以使定位系统具有更多源的数据和更多样的方式。

视觉定位中有很多常用的图像特征，如尺度不变特征转换（scale-invariant feature transform，SIFT）、Harris 角点以及消影点等。消影点是场景中平行线经过透视投影后在图像上汇聚的一点，它仅仅依赖于空间直线的方向，而与其位置无关，将消影点作为视觉定位中图像的描述特征具有独特的优势，有很多学者进行了相关研究。北京理工大学信息学院江泽民等，提出了基于平行线的摄像机参数标定和自主移动平台室内视觉导航算法，利用走廊左右踢脚线构成的一组平行线在视平面上的投影直线的斜率和消影点坐标，来标定摄像机线性模型的内、外参数，获得摄像机的相对位置。卡尔斯鲁厄理工学院系统优化研究所的Christoph Kessler 等利用消影点和消影线，提出基于视觉系统的室内长期稳定姿态估计的一种方法。该研究方向最具代表性的研究团队是芬兰地球空间研究所（原芬兰大地测量研究所）的Laura Ruotsalainen团队，他们讨论了视觉陀螺仪性能误差和避免误差传播的方法。2013年提出了一种基于概率霍夫变换的点提取方法，不仅提高了消影点提取的有效性，还提出了提取转角区域消影点的新方法。中国科学院光电研究院的公续平等，在视觉陀螺仪辅助的行人推算定位方法（KVisGyro aided PDR，KVISPDR）中，创新了消影点的提取方法，首先是提取图像区域直线，然后根据直线斜率将其分为3 类，为每类直线赋予不同的权重，使用直线交点加权的方式计算消影点的位置，提高了消影点的提取精度。

从图像成像特点以及消影点形成原理可知，消影点提取会受到多种因素的影响，包括图像质量、拍照角度、光照条件、动态物体、阴影、非结构建筑等，需要改进消影点提取算法来克服这些问题。本研究提出基于图像梯度场的消影点提取算法，然后根据计算机视觉中的多视图几何实现视觉陀螺仪和视觉里程计，通过位置推算得到视觉定位结果，并将其与行人航迹推算（pedestrian dead reckoning，PDR）估计结果及真实数据进行对比完成精度的验证与评价。通过采用新的消影点提取方法，提高消影点的提取精度及视觉陀螺仪和视觉里程计的性能。算法流程如图1 所示。

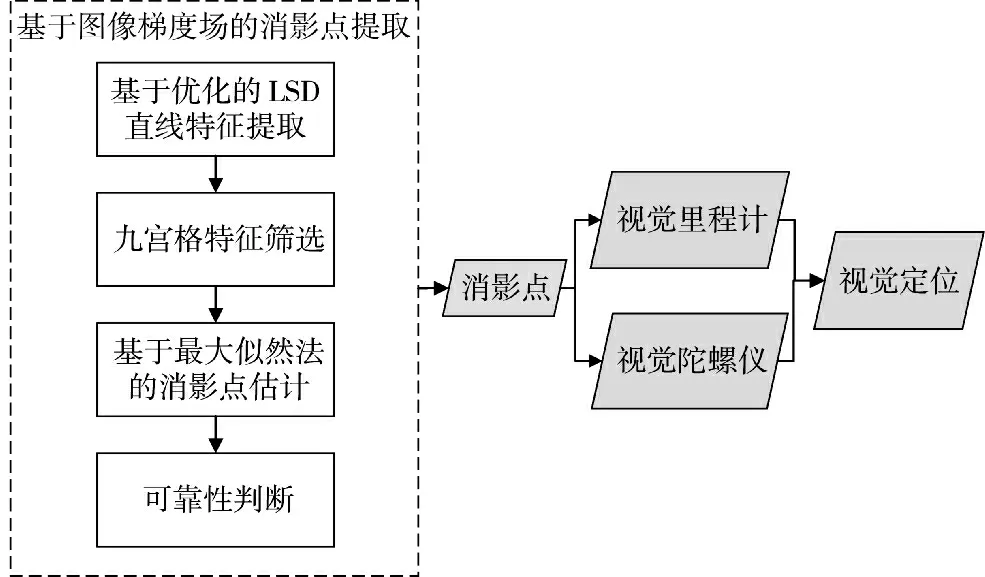
图1 视觉定位算法流程图

1 基于图像梯度场的消影点提取方法

本文提出了一种基于图像梯度场的消影点提取方法（vanishing point extraction based on gradient field，VP-GF），首先利用优化的直线检测算法（line segment detector，LSD）提取直线特征，然后采用双阈值方法筛选出符合条件的特征后利用最大似然法估计消影点，最后通过计算消影点精度因子去掉不可靠数据得到有效消影点。

1.1 基于LSD 优化的直线特征提取

直线检测是利用消影点进行视觉定位的基础工作，本文主要通过优化LSD 算法进行直线提取。LSD 是一种直线段检测算法，可以在线性时间内得出亚像素级别的检测结果。共包括9 个步骤，分别为图像高斯降采样、检测图像梯度、梯度伪排序、设置梯度阈值、区域增长、关联矩形估计、计算误检测数、计算类内点密度、关联矩形调整。整个算法过程共有5 个阈值，分别为高斯降采样尺度、梯度阈值、区域增长的容差、误检测数阈值、类内点密度阈值。本文主要针对室内图像进行直线特征提取，根据室内图像特点，优化以上5 个参数值。通过大量的实验验证，高斯降采样尺度、梯度阈值、误检测数阈值这3 个参数采用原算法的取值效果最好。考虑到程序的运行速度和定位算法的实时性，本文的区域增长容差取π/8。同时，讨论了不同环境（复杂环境和简单环境）中的类内点密度阈值，参考原算法取值并经过大量实验，简单环境中类内点密度阈值取0.7 效果最优，复杂环境取0.6 效果最优。

1.2 特定的直线特征筛选

根据中心消影点的概念及特征，只有在前进方向上延伸的直线对消影点有作用。实际场景中包含大量直线特征，提取到的直线特征包含对消影点无作用的特征；另外，场景中存在的阴影、动态物体、行人等非结构特征会导致直线提取错误，所以需要在估计消影点之前去掉无作用及错误的直线特征，从而提高消影点的可靠性。根据以上分析，本研究采用双阈值筛选直线特征的方法：

1）根据线段长度进行筛选，过短的直线可能是由于环境中无关物体或阴影形成，通过设定阈值过滤掉小于该值的直线段，取实验经验值为10 像素。

2）根据线段倾斜角度进行筛选，根据消影点形成原理可知，环境中沿运动方向延伸的直线对消影点有贡献，其余的线段为干扰特征，这些特征可以通过设定线段倾斜角度阈值过滤掉。根据透视投影的特点，在现实世界中平行的直线在图像上会有不同的倾斜角度，也就是说同样都是沿运动方向延伸的直线，它们在图像上的倾斜角度差异会非常大，所以在利用线段倾斜角度筛选特征的时候不能只设置一个阈值。本文将图像划分为九宫格，每格为一个区域，如图2 所示，按照直线特征所处的区域设定斜率阈值，根据成像特点，设定4 个阈值，在阈值范围内的线段被过滤，第1、3、7、9 区域阈值相同，取实验经验值为水平方向±20°，垂直方向±20°；第2、8 区域阈值相同，取实验经验值为水平方向±20°；第4、6 区域阈值相同，取实验经验值为垂直方向±20°；第5 区域阈值取实验经验值为水平方向±10°，垂直方向±5°。

图2 设置线段倾斜角度阈值的九宫格分区

直线特征筛选后，根据直线段的倾斜角度将其分为3 类，分别对应3 个轴的消影点，这里只关心对应中心消影点（Z 轴）的直线段。

1.3 基于最大似然法的消影点估计

本文使用最大似然估计算法（maximal likelihood estimation，MLE）来估计消影点，该算法是寻找一组通过某一点的直线，直线的数量与检测到的直线段数量相等，且直线段的两端点到这组直线的正交距离最小。用公式表达为：

1.4 消影点可靠性判断

理论上，场景中不同位置沿前进方向的平行线在图像上呈现为不同斜率的射线，且射线的端点均为消影点。所以，现实中平行且图中斜率差别越大的线相交得到的消影点越可靠，参考文献［6］中的方法，以消影点为原点，将图像分为4 个象限，本文将各个象限中过消影点的线段数与图像上经过消影点的线段总数的比值，作为消影点精度因子来判断消影点的可靠性。根据消影点形成原理及本文中消影点提取的方法，以下情况认为消影点可靠：1）4个象限都有穿过消影点的线段，如图3（a）所示；2）有任意3 个象限中都有穿过消影点的线段；3）相邻的两个象限中有穿过消影点的线段，如图3（b）所示。

图3 以消影点为原点将图像分割成4 个象限

以下情况认为消影点可靠性低或不可靠：

1）由相对的两个象限中的线段估计得到的消影点可靠性低，如果参与估计的线段数过少则认为该消影点不可靠，如图3（c）所示；

2）仅由一个象限中的线段估计得到的消影点不可靠，如图3（d）所示。

假设各个象限内参与消影点估计的线段数为l（i=1，2，3，4）（l为第一象限内参与消影点估计的线段数），图像上参与消影点估计的线段总数为L。根据以上描述，消影点不可靠时以下公式成立：

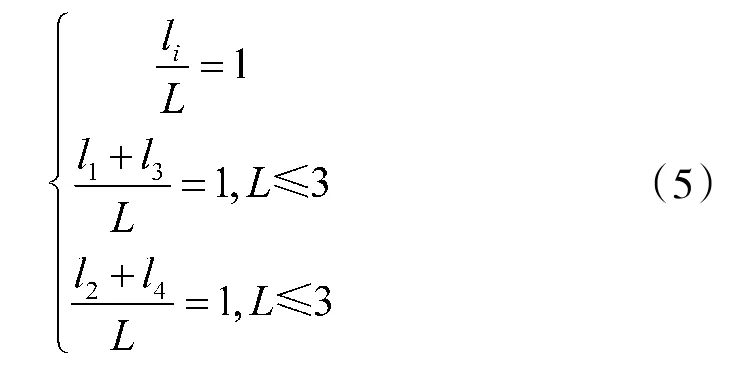
在进行视觉陀螺仪和视觉里程计的计算前将不可靠的消影点剔除。

2 基于连续图像消影点的视觉定位

2.1 视觉陀螺仪

利用连续图像特征的位置变化解算相机朝向、横滚和俯仰的方式，被称为视觉陀螺仪，即获得相机的外方位元素。根据对极几何关系，假设相机的标定矩阵为K，连续两幅图像对应的摄像机欧氏坐标系的旋转矩阵为R，令一条直线在第1 幅图像中经过的消影点为v，在第2 幅图像中为v'，消影点v在第1 个摄像机的欧氏坐标系中测量得到的方向为d，而对应的消影点v'在第2 个摄像机的欧氏坐标系中测量得到的方向为d'。用消影点来计算方向：d=Kv/‖Kv‖，方向d和d'通过摄像机的旋转d'=Rd相关联，这就给出了关于R 的两个独立约束。图像上相机消影点位置的变化可以用相机标定矩阵K 表示，标定矩阵K 包含相机的内参数，分别为焦距（f，f）和主点坐标（u，v）。图像中消影点的位置可以表示为V=［vvv］=KR，连续图像的相机朝向角变化为θ，俯仰角为φ，如果两个角同时发生变化，得到旋转矩阵R 为：

可以根据消影点位置变化得到：

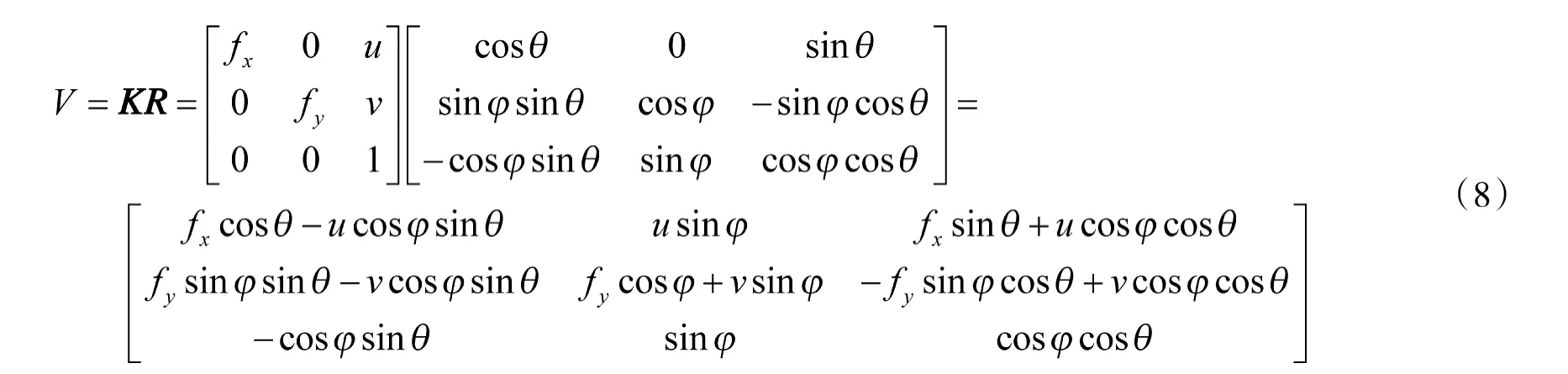
2.2 视觉里程计

视觉里程计利用连续图像之间的单应性恢复深度、距离信息。同一个现实世界的点在连续两幅图像上分别表示为x 和x'，由单应性得到两者关系：x'=K'RKx+K't/Z。其中，Z 表示相机到对象的距离，t 表示移动的距离，K 为相机的已知内参数，R 是旋转矩阵。根据单应性原理，得到相机到对象的距离Z，便可以计算得到平移距离t。相机到对象的距离Z 的计算方法：相机的高度h，焦距f，图像的高度H，相机的高度是已知的，焦距和图像的尺寸可以在相机校正时获得。物体的坐标为（X，Y，Z），投影到图像上的坐标为（x，y），相机与地面的倾角φ 由视觉陀螺仪求得。当图像高度和焦距的垂直分量已知，则垂直视场（vertical field of view，VFOV）为：

2.3 位置推算

得到视觉陀螺仪和视觉里程计后进行位置推

3 实验结果及分析

3.1 实验环境构建

实验区域选取在北京大学理科教学楼。这是一个典型的现代教学楼环境，包括较为开阔的大厅和狭长的走廊，在开阔的大厅中有沙发、桌椅、饮水机等基础设施，并且建筑的室内结构不明显，本文将其定义为复杂环境。狭长的走廊以墙壁、门窗、天花板、地板等建筑要素为主，本文将其定义为简单环境。这两种环境均为教学楼内常见环境。实验场景如图4 所示。图中实心圆点（含红点与蓝点）为路线点。

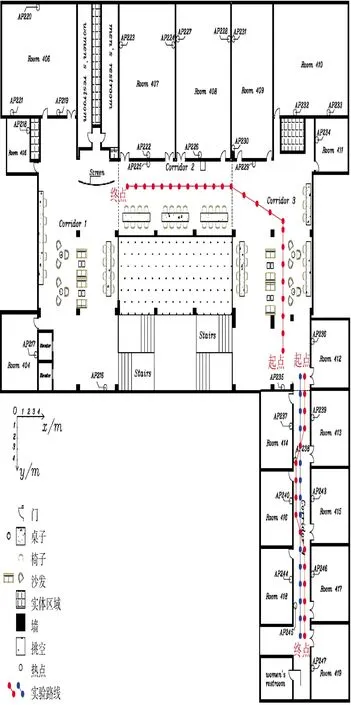
图4 视觉定位实验平面图

根据精度验证的需要，实验分为两部分：

1）简单环境实验，该实验在狭长的走廊完成，实验的路线在corridor4，包含两条实验路线，路线1为全部直行（蓝色），其长度约为24 m，路线2 包括转弯和直行（红色），其长度约为24.76 m；

2）复杂环境实验，该实验在开阔的大厅完成，实验的路线穿过corridor2 和corridor3，记为路线3，其长度约为41.32 m，包含两次转弯。

实验获得的数据为实时图像数据，获取频率约30 Hz；加速度、陀螺仪、磁力计数据，获取频率约200 Hz。

3.2 视觉陀螺仪性能评估

根据实验设计，路线1 和路线2 属于简单环境，路线3 属于复杂环境，且路线2 和路线3 中有转弯区域，在视觉陀螺仪性能评估中需要对不同情况进行分开讨论，并将其与真值和惯性测量单元（inertial measurement unit，IMU）得到的朝向值进行对比。本实验中描述精度的参数为：平均误差（mean error，MeanE）、均方根误差（root mean square error，RMSE）、最大误差（maximum error，MaxE）和最小误差（minimum error，MinE）。为了方便展示，本文为简单环境和复杂环境中的路线建立不同的角度参考系，路线1 中平面坐标系y 轴的负方向为0°，路线2和路线3 朝y 轴的正方向为0°。

图5 为路线1 中视觉陀螺仪与IMU 朝向和真实朝向的对比，从图中可以看出IMU 朝向比视觉陀螺仪朝向的误差更大。

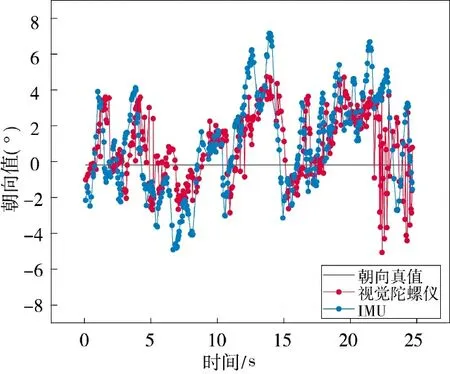
图5 路线1 中视觉陀螺仪与IMU、真实朝向的对比

图6 为路线2 中视觉陀螺仪与IMU 朝向和真实朝向的对比，可以看出视觉陀螺仪的朝向值更接近于真实值。图6 右图为左图虚线框中的转弯部分数据，可以看出视觉陀螺仪的值波动比较严重。

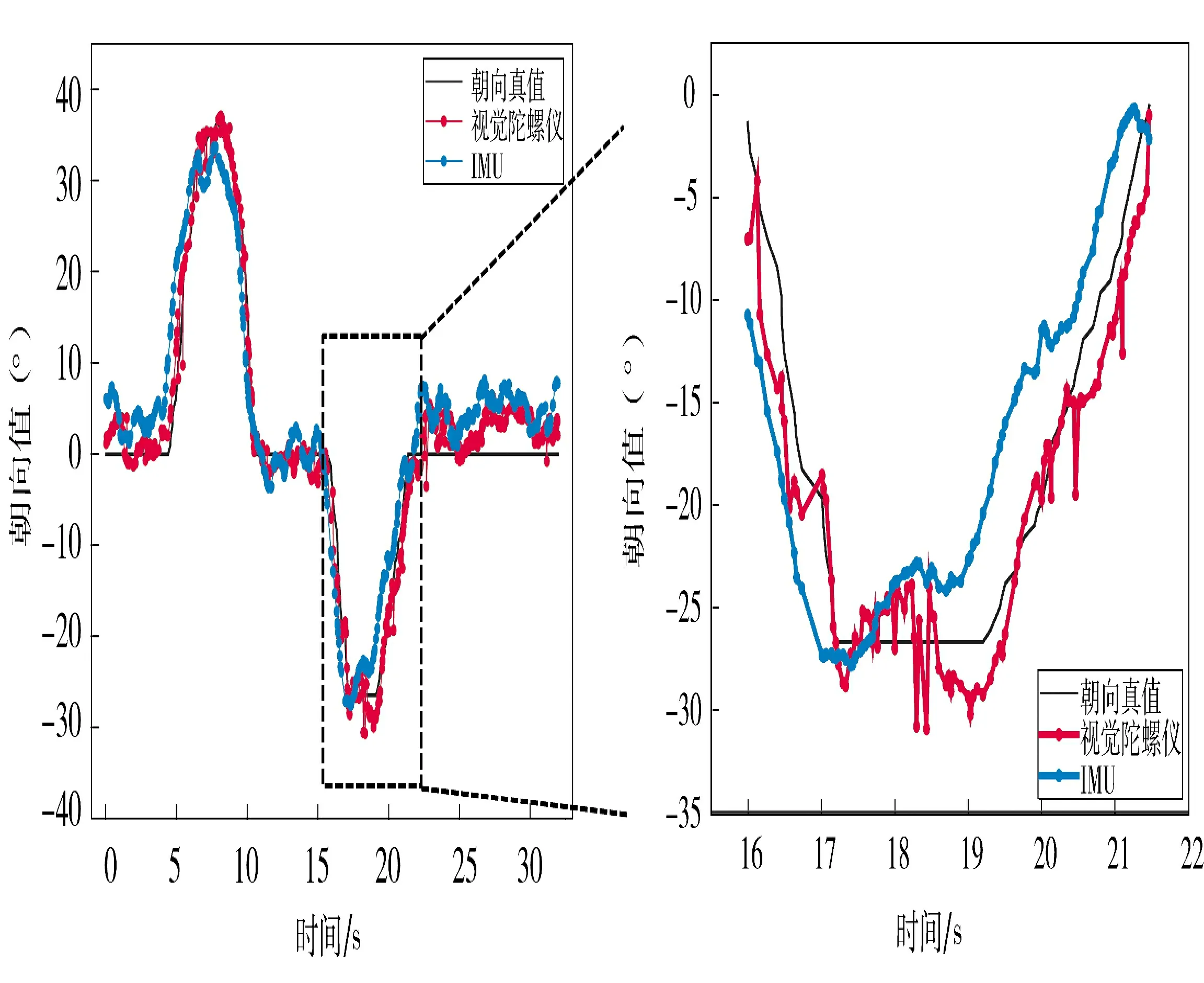
图6 路线2 中视觉陀螺仪与惯导、真实朝向的对比

图7 为路线3 即复杂环境中视觉陀螺仪与IMU 和真实朝向的对比，右图为左图虚线框中的转弯部分数据，类似于路线2 中的情况，视觉陀螺仪的朝向值更接近于真实值，准确度更高。当真实朝向为非0°和90°时，视觉陀螺仪的值波动严重，也就是精确度较低。

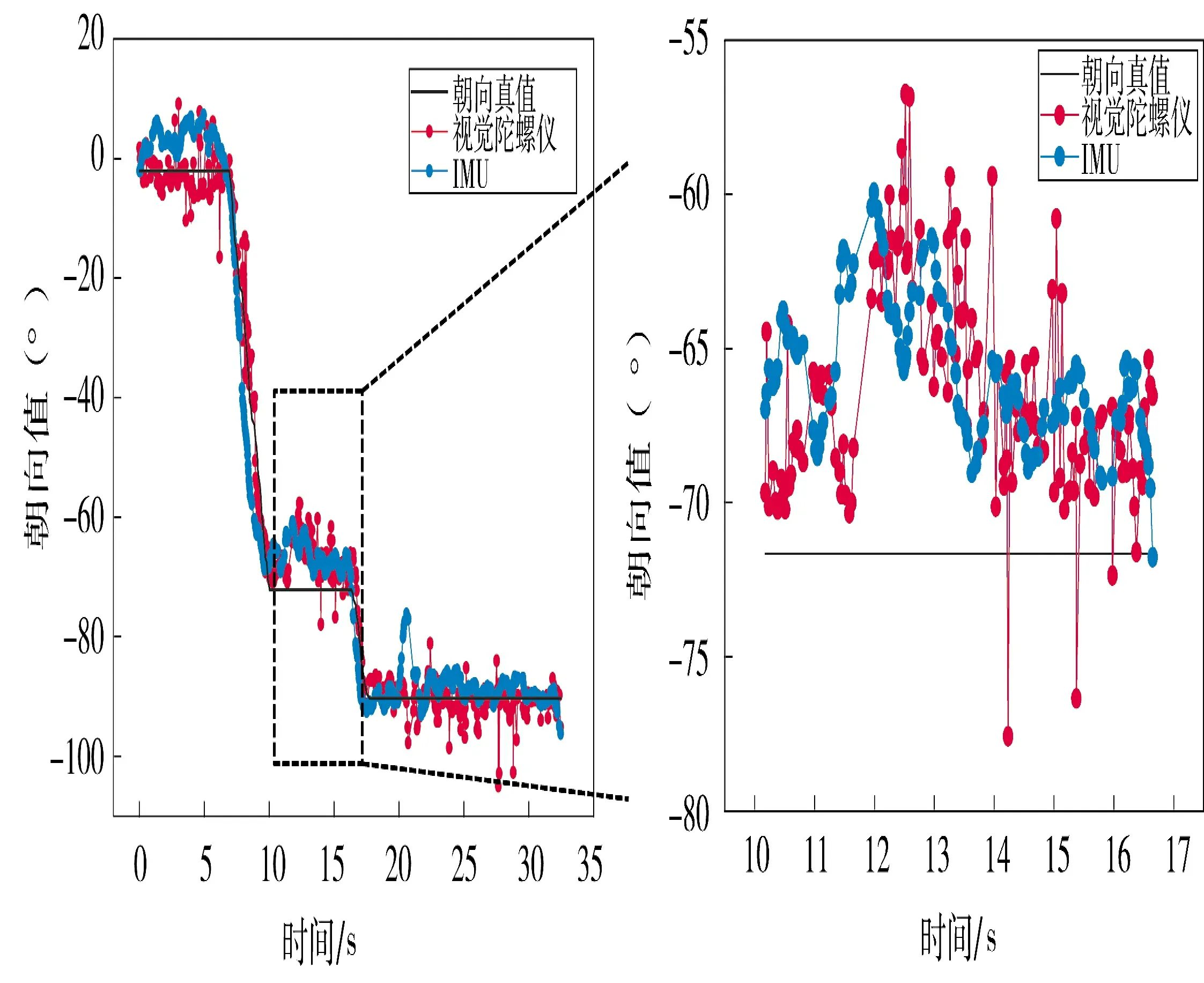
图7 路线3 中视觉陀螺仪与IMU、真实朝向的对比

为了能够定量化地比较视觉与IMU 估计朝向的精度，分别计算了不同情况下的性能参数，如表1 所示。

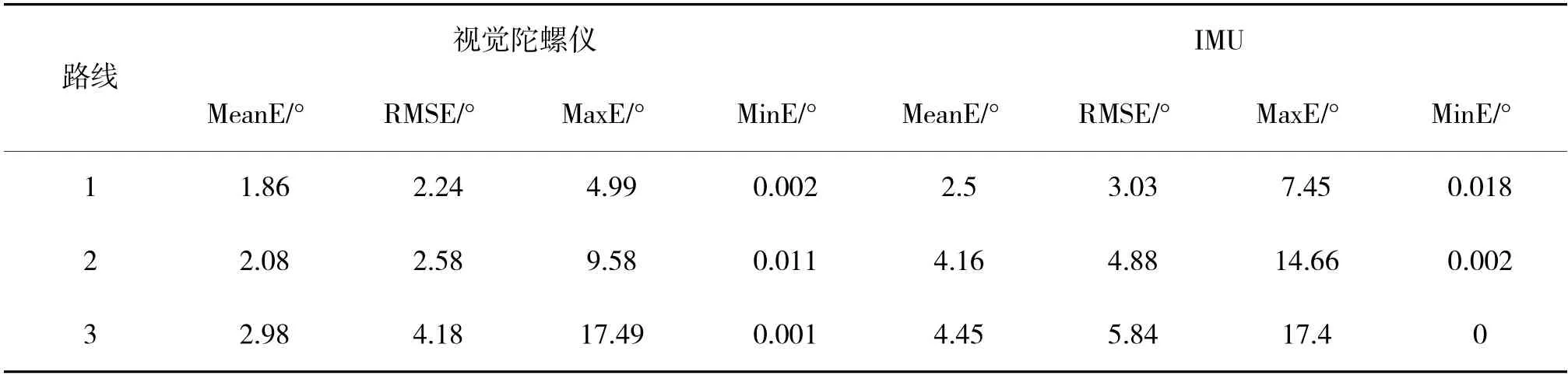
表1 各条路线的朝向估计误差

图8 为视觉陀螺仪和IMU 朝向估计的误差及其累积分布图。从图中可以看出，IMU 的误差累积比视觉陀螺仪更严重。

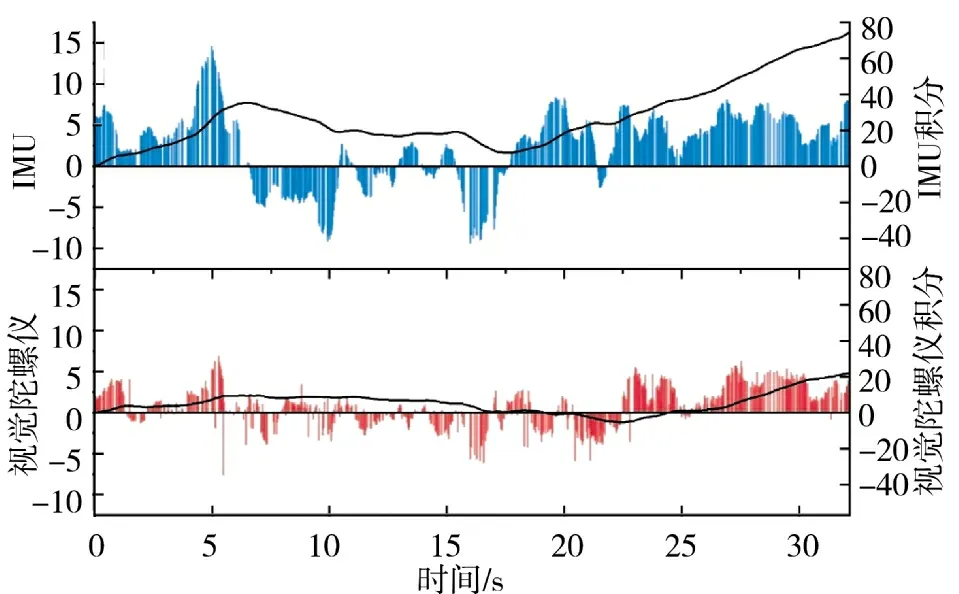
图8 路线2 中朝向误差及其累积

为了进一步验证本文中视觉陀螺仪的性能，选取了芬兰地球空间研究所Laura Ruotsalainen 团队的研究成果进行对比，同样也分为简单环境和复杂环境的情况。文献［16］在狭长的走廊中采用手持手机的姿势完成实验，与本文的简单环境实验相似，平均误差为2.1°，最大误差为9.9°，本文的视觉陀螺仪在简单环境中无论有无转弯其平均误差和最大误差均低于上述结果，误差对比如表2 所示。文献［17］在典型的教学区室内完成实验，与本文的复杂环境相似，其平均误差为4.4°，误差对比如表3所示，本研究的视觉陀螺仪平均朝向误差相比下降了32.3%。

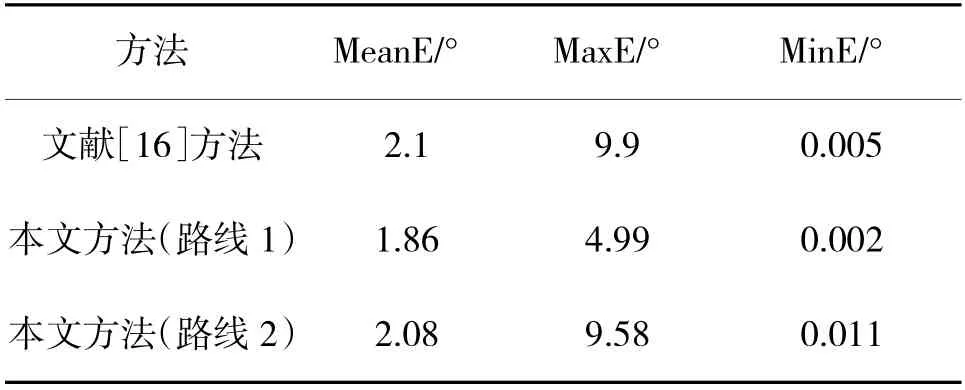
表2 简单环境中视觉陀螺仪与现有方法误差对比

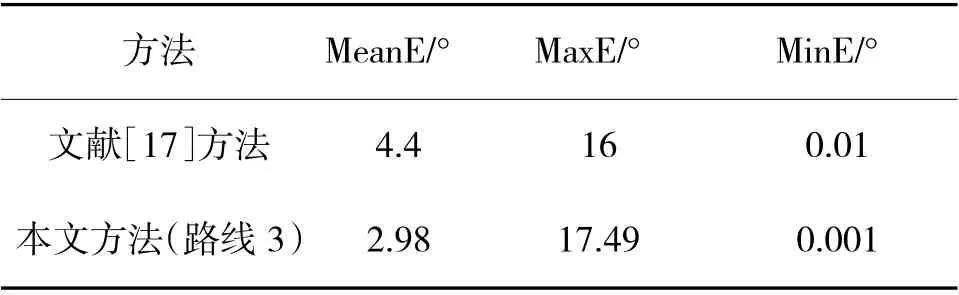
表3 复杂环境中视觉陀螺仪与现有方法误差对比

3.3 视觉里程计性能评估

因为行人在跨步时加速度呈现规律变化，所以加速度计常常被用于跨步检测，跨步检测时能够得到步频，通过公式得到步长后便可以得到跨步时的瞬时速度。视觉里程计得到的结果为相邻图像间的位移，为了方便与IMU 获得的瞬时速度进行比较，这里将视觉里程计的位移转换为瞬时速度，并与真实的全程平均速度进行比较。图9 和图10 分别为路线2 和路线3 视觉里程计与IMU、真实速度的对比，从图中可以看出，这两条路线中IMU 估计速度的整体精度要高于视觉里程计。

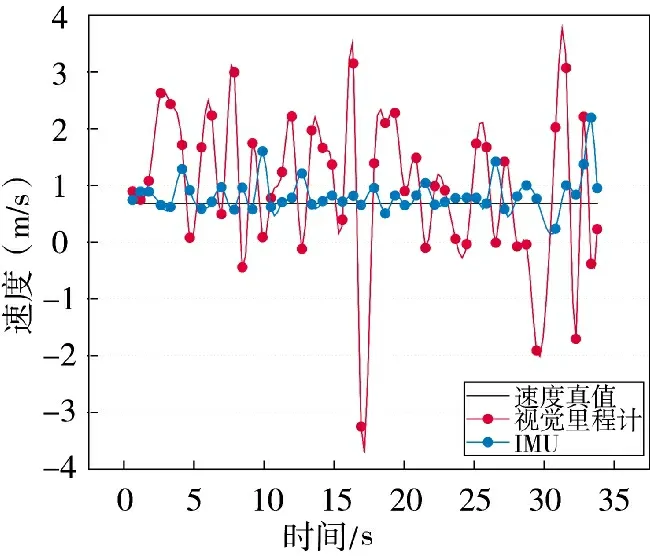
图9 路线2 中视觉里程计与惯导、真实速度的对比

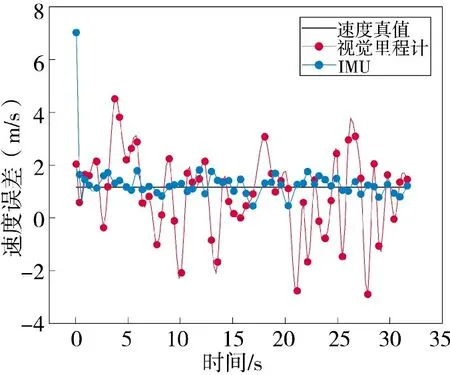
图10 路线3 中视觉里程计与惯导、真实速度的对比

为了比较与分析视觉里程计和IMU 在各个数据点的精度，本实验将误差进行单独展示，如图11和图12 所示，图中的红色误差棒表示视觉里程计的误差，蓝色误差棒表示IMU 的速度估计误差。虽然IMU 的整体精度要高于视觉里程计，但是也有一些数据点视觉里程计的精度更高，如图中黑色箭头所指的数据点。

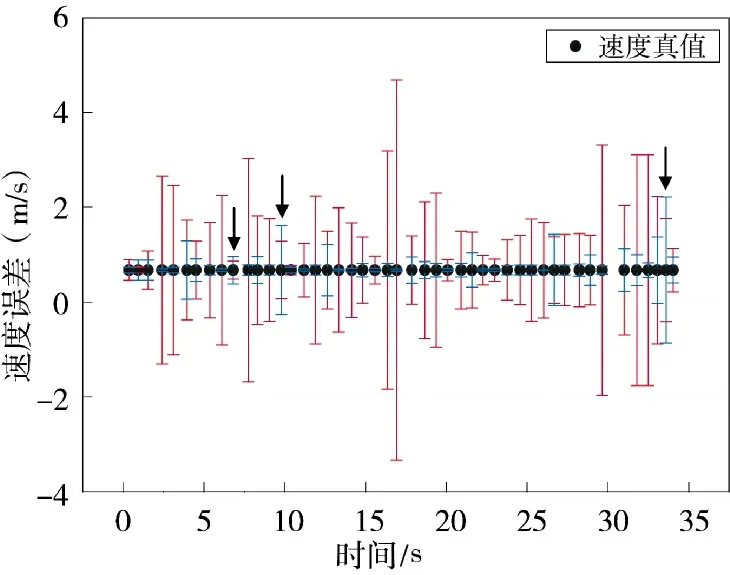
图11 路线2 中视觉里程计与惯导的速度误差比较

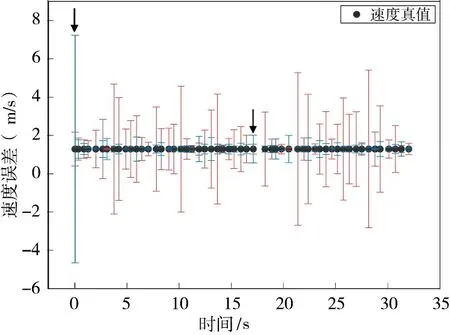
图12 路线3 中视觉里程计与惯导的速度误差比较

3.4 位置估计性能评估

本节从简单环境和复杂环境分别对视觉陀螺仪和视觉里程计推算的位置进行性能评估，图13和图14 分别为简单环境和复杂环境中的视觉定位结果。从图中可以看出，视觉定位的趋势与真实路线大致相符，说明视觉陀螺仪的准确度较高。但是估计位置与实际位置相差较大，定位点的分布不规则，主要是由于视觉里程计的准确度较低，且估计的每段位移差别较大。表4 为视觉定位的参数统计结果，可以看出，简单环境中视觉定位的精度高于复杂环境。

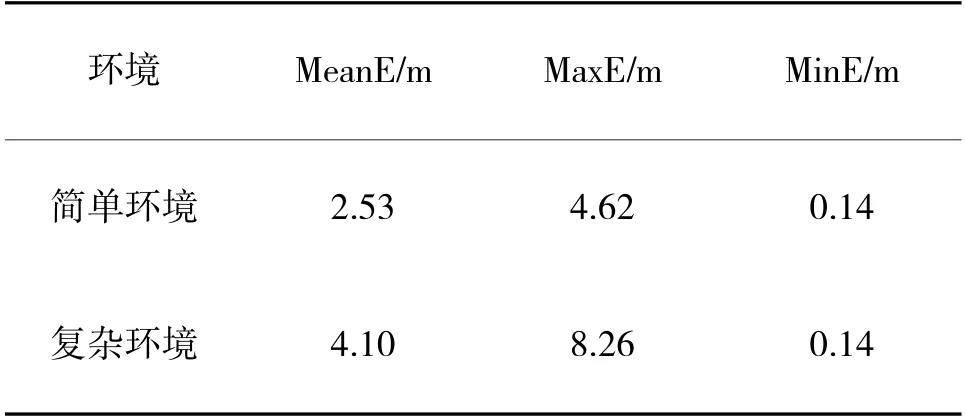
表4 不同环境中视觉定位精度

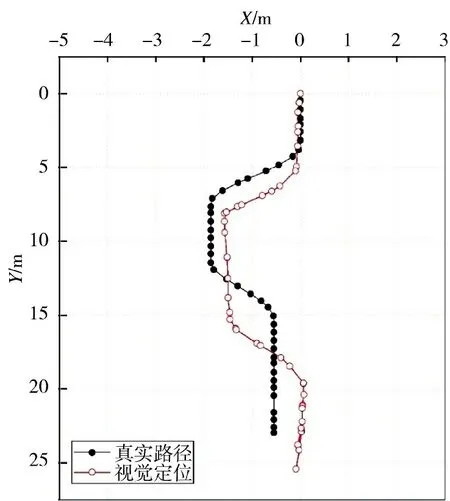
图13 简单环境中视觉定位结果图

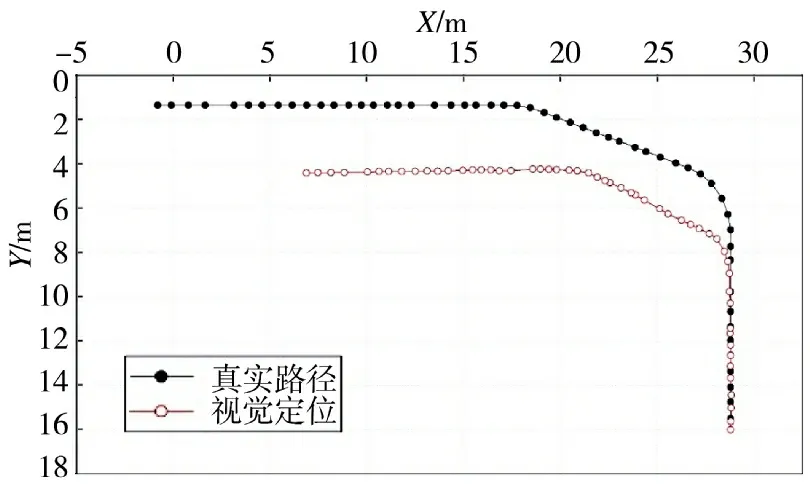
图14 复杂环境视觉定位结果图

4 结论

现有视觉定位算法复杂度高，容易受到图像质量、拍照角度、光照条件、动态物体及非结构建筑等影响。本文针对这些问题，将消影点作为图像的描述特征，首先利用LSD 算法提取直线特征，将室内环境分为简单环境和复杂环境进行参数讨论，使算法在这两种环境中达到最优状态；采用双阈值方法筛选直线特征，根据透视投影成像特点，提出了九宫格分区确定阈值的方法；然后利用最大似然法估计消影点，减少直线特征提取偏差的影响；最后通过计算消影点精度因子去掉不可靠数据，以保证在后续视觉陀螺仪和视觉里程计的计算中均利用了有效消影点。在实测实验中，分别就简单环境和复杂环境进行讨论，视觉陀螺仪整体准确度优于IMU朝向估计结果，简单环境中视觉陀螺仪的平均误差为1.86°（无转弯）和2.08°（有转弯），复杂环境中的平均误差为2.98°。通过与芬兰地球空间研究所Laura Ruotsalainen 团队对视觉陀螺仪的研究成果进行对比，本文的方法提升了视觉陀螺仪精度，复杂环境的平均朝向精度提升了32.3%。速度和累计距离估计中IMU 的整体准确度优于视觉里程计，但是在某些数据点视觉里程计的准确度反而更高，在多源数据融合定位中可以利用这些点的优势来辅助降低定位误差。本文研究主要面向同水平面场景，现实生活中存在很多非水平面场景，所以非水平面的视觉定位将成为下一步的研究方向。