求解电子对抗兵力规划问题的改进型混合遗传算法*

赵禄达，王 斌，2*，巴根那

（1.国防科技大学电子对抗学院，合肥 230037；2.国防科技大学第三学科交叉中心，合肥 230037；3.解放军77126 部队，云南 开远 661699）

0 引言

兵力规划问题的核心就是在作战全过程动态、变化地调整兵力的分配、部署和运用，以适应现代化作战需求，保持部队战斗力。电子对抗作为现代智能化战争的重要组成部分，其作战过程中的兵力规划就显得尤为重要。电子对抗兵力规划问题是武器目标分配问题（weapon target assignment，WTA）的一种拓展形式，且WTA 被证明是NP 难问题。近年来，许多中外学者对此问题进行了深入研究。主要集中在两个方面，即不同作战样式、武器下的建模问题和解决WTA 问题的算法研究。文献［3］建立了现代战争中密集型空对地武器的目标编成模型，并加入了干扰约束条件，但文章解法较为简单且推广性不够；文献［4］在总结一般WTA 的基础上推广了S-WTA 模型，并提出了加入修复机制的改进型遗传武器编成算法（GA-SWTA），得到了比较好的收敛解空间；在此基础上文献［5-6］将表征主观因素的信念熵和优化装备系统的数据进行融合研究，结合免疫算法提出了改进的分解协同算法（DCEA-AGWTA）和混合遗传算法（HGA），使算法性能在原模型基础上有所改进；文献［7］将启发式遗传算法和量子遗传算法相结合，提出了多目标量子启发式遗传算法（Mo-QIGA），较好地解决了战场武器规划问题；文献［8］将混合灰狼算法（DGWO）运用到WTA 问题的求解中，经验证算法收敛性较好。在研究电子对抗兵力规划问题上，文献［9-10］采用改进的自适应遗传算法对雷达对抗干扰系统进行了兵力分配问题的讨论；文献［11］采用量子遗传算法，研究了电子对抗兵力在地空反辐射群编组中的编成优化问题，但由于初始样本是随机产生的，有可能最终得不到全局最优解，算法的全局寻优能力需要进一步加强；文献［12］利用混沌搜索算法对雷达干扰兵力进行了优化分配，但由于算法中加入了雷达威胁主观系数因子，导致算法的客观实际应用性降低。

1 任务背景构建

在以任务为牵引的作战背景下，从作战实际出发将整个问题背景空间分为作战筹划空间、战斗实施空间和算法空间3 部分，如图1 所示。

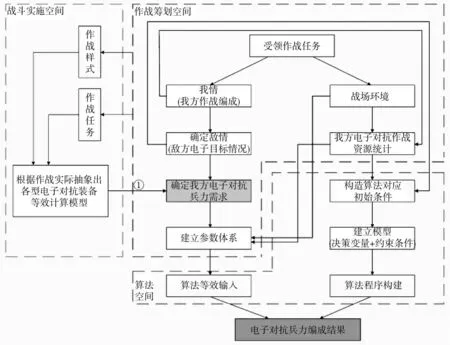
图1 作战任务背景空间组成示意图

作战筹划空间是指合成部队从受领作战任务开始的一系列作战准备工作，电子对抗分队需要从合成部队总体筹划中确定自身的初始情报和作战参数。在我方受领作战任务后，电子对抗分队需要确定我方任务中电子对抗兵力作战编成（装备数量、人员等），敌方电子目标相关情况（类型、数量等）以及作战地域战场环境相关参数（地形、天气等）。另外，在作战筹划的过程中需要确定战斗的作战样式及作战具体任务，为具体实施作战时能够正确选择恰当的作战模型。

战斗实施空间是指在战斗发起后（T 时后）电子对抗分队指挥员根据战场实际，结合我方作战任务和作战筹划选定的作战样式，选择电子对抗装备的等效计算模型，快速得出我方作战效能。另外通过改进的Lancherster 信息战模型（图1 中箭头①）得出敌我双方电子兵力比，从而得到兵力编成的初始兵力集合。

算法空间是指在作战筹划空间和战斗实施空间接续实施的并行空间，输入为战斗实施空间得出的兵力编成初始集合和作战筹划空间得出的模型构建初始条件。一方面建立初始条件作为约束的电子对抗兵力编成模型，另一方面建立改进型遗传算法结构，最终将模型输入带入算法进行解模，得到最终的电子对抗兵力编成结果，为电子对抗指挥员提供快速可靠的决策建议。

2 电子对抗兵力规划模型

2.1 模型符号说明

电子对抗兵力编成模型及本文中相关符号含义及其说明如下页表1 所示。

表1 符号含义及说明

2.2 模型构建

本文中电子对抗兵力编成模型建立如下：

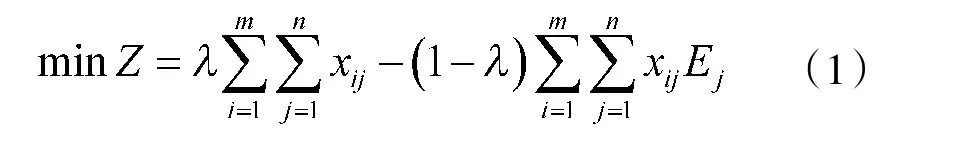
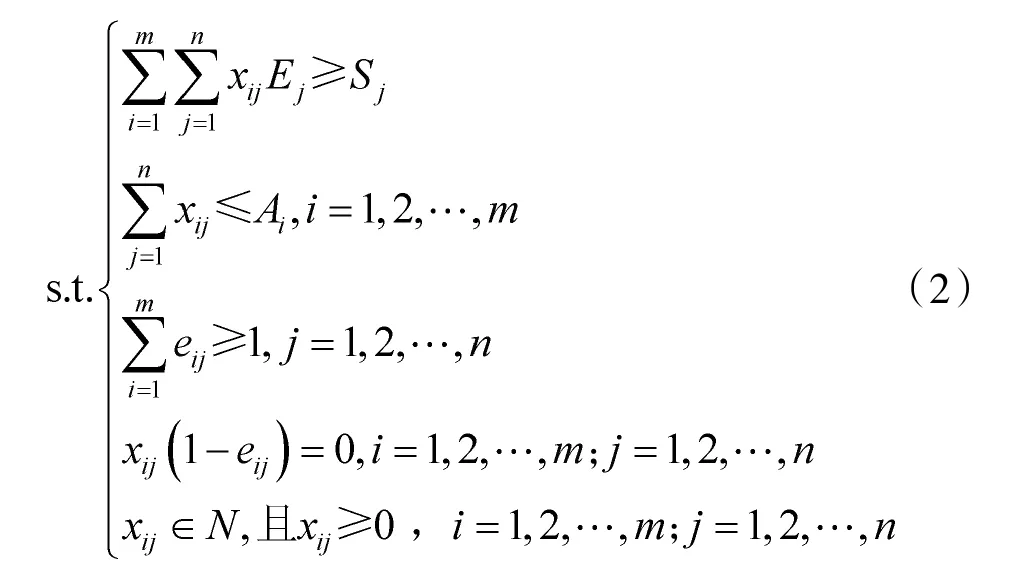
其中，式（1）为模型目标函数，表示电子对抗进攻的效能需求和装备的数量需求。式（2）为模型的约束条件，共有5 个约束，第1 个约束表示我方对敌方第j 类电子目标实施进攻的总效能不低于对敌方第j 类目标有效干扰的效能阈值；第2 个约束表示我方参与电子进攻的第i 型电子对抗装备数量不得超过我方编成内第i 型电子对抗装备总数量；第3 个约束表示将我方电子对抗装备利用率达到最大（至少有1 型电子对抗装备对敌第j 类目标实施进攻）；第4 个约束为等式约束，表示0～1 变量e与决策变量x之间的等式关系；第5 个约束为决策变量x的取值约束，要求其为大于等于0 的正整数。

3 基于改进型混合遗传算法的兵力规划模型解法

遗传算法模拟生物自然选择进化过程，进行不同代数解集的优胜劣汰，在规划寻优问题上得到了广泛应用。算法过程一般为确定初始种群、确定适应度函数和个体的适应度值、遗传操作（选择、交叉、变异等）、种群优化判断等步骤。本文将利用改进的Lanchester 信息战模型对初始种群进行初始化，改变传统的随机选择和自适应选择的种群不确定性，并将传统遗传操作进行改进，让遗传操作的种群与父代中延续的种群进行混合，增加父代个体的延续性，目的是提高模型算法的全局收敛能力和收敛速度。改进型混合遗传算法步骤如图2 所示。

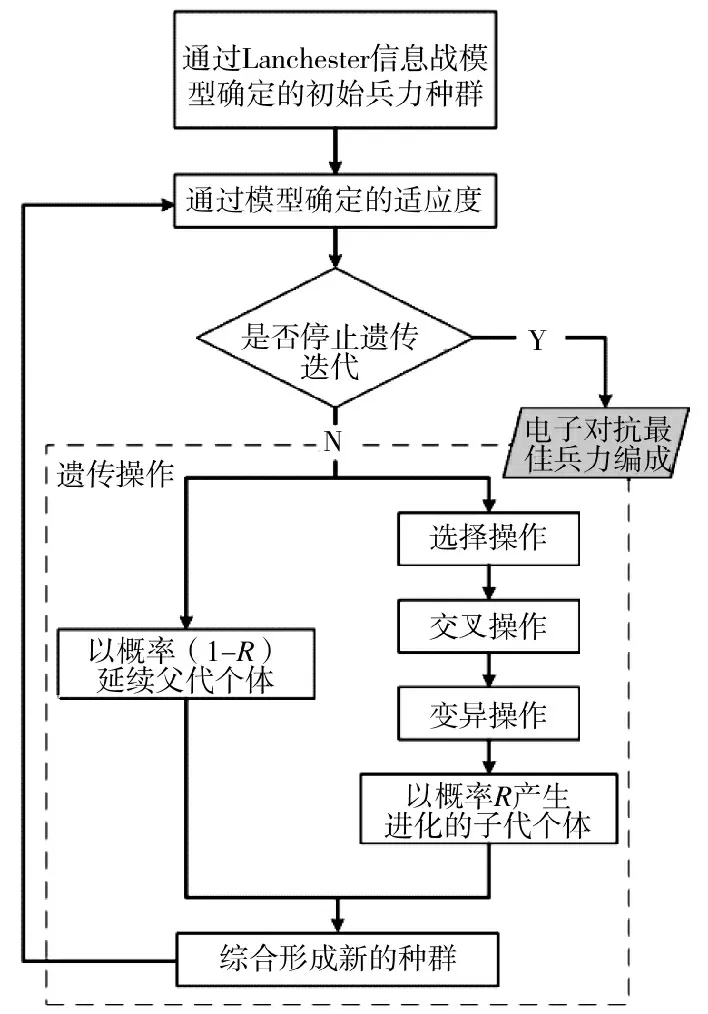
图2 算法步骤示意图

3.1 种群初始化

种群的初始化编码目的是为了建立满足约束条件的电子对抗兵力编成方案与便于遗传操作的染色体之间的关系，本文采用二进制编码手段对初始种群进行编码，如图3 所示。

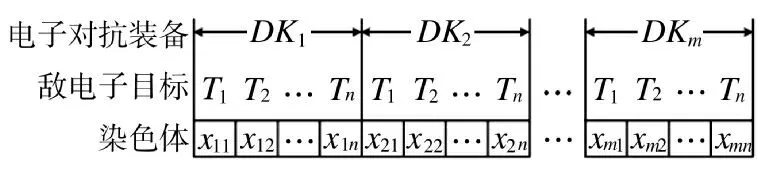
图3 种群编码方式

敌方电子目标数量为n，将染色体编码为m 段，每一段表示我方电子对抗装备的一个进攻组合（编成）方案，遗传操作（选择、交叉、变异）均在段内进行。可以得出，每个电子对抗装备对应的染色体基式中，r-r 和b-b 表示我方和敌方信息战总体能力的变化。由于双方的信息对抗，我方的信息量损耗率与我方信息损耗变化值和敌方信息对抗引起的信息量损耗率之积成比例，也和信息的自然损耗和补充有关。在信息战模型的基础之上，考虑电子对抗因素，加入由于电子对抗引起的信息量变化系数ε，得到改进的Lancaster 信息战模型，如式（4）所示。

3.2 适应度函数的确定

适应度函数是为了对初始种群和遗传操作后的种群进行目标函数值判断寻优而建立的。而文中建立的模型中目标函数为最小值目标，在算法过程中一般采用最大值进行寻优筛选，则将适应度函数定义为式（1）的相反函数，如式（5）所示。

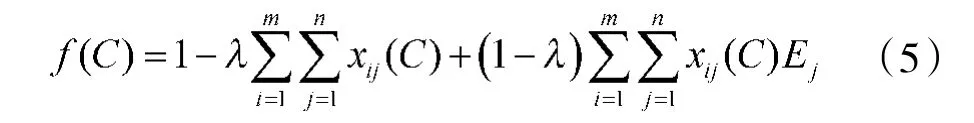
3.3 遗传操作

在确定了初始种群和适应度函数后，对种群进行选择、交叉、变异等遗传操作，在规定的最大遗传代数约束下最终停止遗传操作。现将其中的核心操作选择、交叉、变异简述如下，其操作如图4 所示。

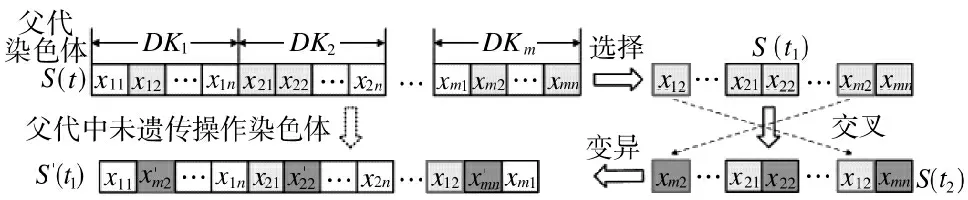
图4 模型遗传操作示意图

2）交叉：采取双点交叉的方式进行操作。在选择出的种群（染色体）中随机选择两处基因进行交叉互换操作，得到新的种群S（t）。

3）变异：采取有效基因突变方法进行。将交叉得到的种群进行随机基因位突变，由于编码采取二进制，突变基因只需进行0 或1 的变化，即得到新种群S（t），与父代中为进行遗传操作的基因进行综合就可得到最新的种群。

4）种群的综合：按照概率R 对父代种群和经过以上3 步后的变异种群进行混合，得到适应性函数求解的种群S（t）。

4 算例仿真与分析

这一部分主要分为以下两个方面：一是对本文建立的模型和提出的改进型遗传算法进行算例仿真，表明模型有效性和算法可行性；二是对算法进行性能对比仿真，通过与标准的遗传算法（GA）、免疫遗传算法（IGA）以及自适应遗传算法（AGA）进行对比，表明不同算法在解决相同模型上的优劣。仿真实验采用的仿真平台CPU 为i7-5580 H，2.60 GHz，16.0 GB RAM，操作系统为Windows10，仿真实验工具为Matlab R 2018a。

4.1 任务背景构建及仿真

首先根据任务背景构建作战筹划空间和实施空间数据：我方在任务中派遣光电对抗装备18 台，雷达对抗装备16 台，通信对抗装备12 台；根据先期情报敌方光电设施（装备）6 台，雷达设施（装备）5台，通信设施（装备）3 台；由于战场环境影响造成的双方电子信息损耗系数为μ=μ=0.5；不同类型电子对抗装备对应的电子战效能损耗ρ=0.4，ρ=0.5。其次设定遗传算法输入数据：种群数量为100；遗传代数为200；总变量个数为3×3=9 个；目标数量为3；选择概率为0.8；交叉概率为0.7；变异概率0.03；种群混合概率R 为0.3；假设双方没有信息支援力量，信息补充量V=0；电子对抗影响下的作战效能因子ε=0.8，ε=0.7。

仿真得到的结果如表2 所示，算法运行结果如图5 所示。其中图5（a）表示随着遗传代数的增加种群适应度值的变化，将每代种群中的最优、最差以及平均适应度值进行统计，绘制而成3 条曲线。可以看出，在遗传代数达到48 代之后，种群适应度趋于稳定，最优适应度值为13.086 2。图5（b）表示在种群达到了最优适应度值后的每一代最优适应度值连线，可以看出，除了第62 代和132 代以外，达到稳定后的各遗传代数均达到了全局最优的适应度值，使用改进型的遗传算法解决本模型获得很高的成功率。此外，对模型进行计算时对每一代进行程序调试，除第62 代和132 代以外，其余代数的迭代时间最多为4.61 s，最少为2.15 s，可见算法的效率很高。

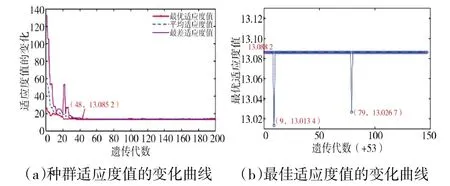
图5 算法运行仿真结果

表2 仿真得到的电子对抗兵力规划结果

表中，T代表敌光电目标，T代表敌雷达目标，T代表敌通信目标；DK代表我光电干扰装备，DK代表我雷达电干扰装备，DK代表我通信干扰装备。

4.2 算法性能对比

本节主要对本文建立的改进型遗传算法进行算法对比仿真，通过与GA、IGA 和AGA 3 种遗传算法进行对比，体现本文构建的算法在解决电子对抗兵力编成模型时的高效率和准确性。

首先按照对比试验的要求，生成5 个想定，如下页表3 所示。

表3 5 组想定对比仿真数据生成

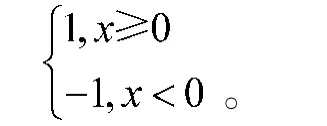
其次，设定作为对比的3 种遗传算法输入参数。为严格控制变量，参数与本文构设的改进型遗传算法输入数据与4.1 节中一致（种群数量为100；遗传代数为200；选择概率为0.8；交叉概率为0.7；变异概率0.03；信息补充量V=0；电子对抗影响下的作战效能因子ε=0.8，ε=0.7）。

对模型进行仿真得到的数据进行分析，取每种遗传算法适应度函数值趋于稳定后的数据（趋于稳定的代数为：本文算法48，GA 为59，IGA 为47，AGA 为51。综合选择60 代之后的数据），共4 组，每组160 个数据，进行方差分析，得到分析结果如表4 和下页图6 所示。

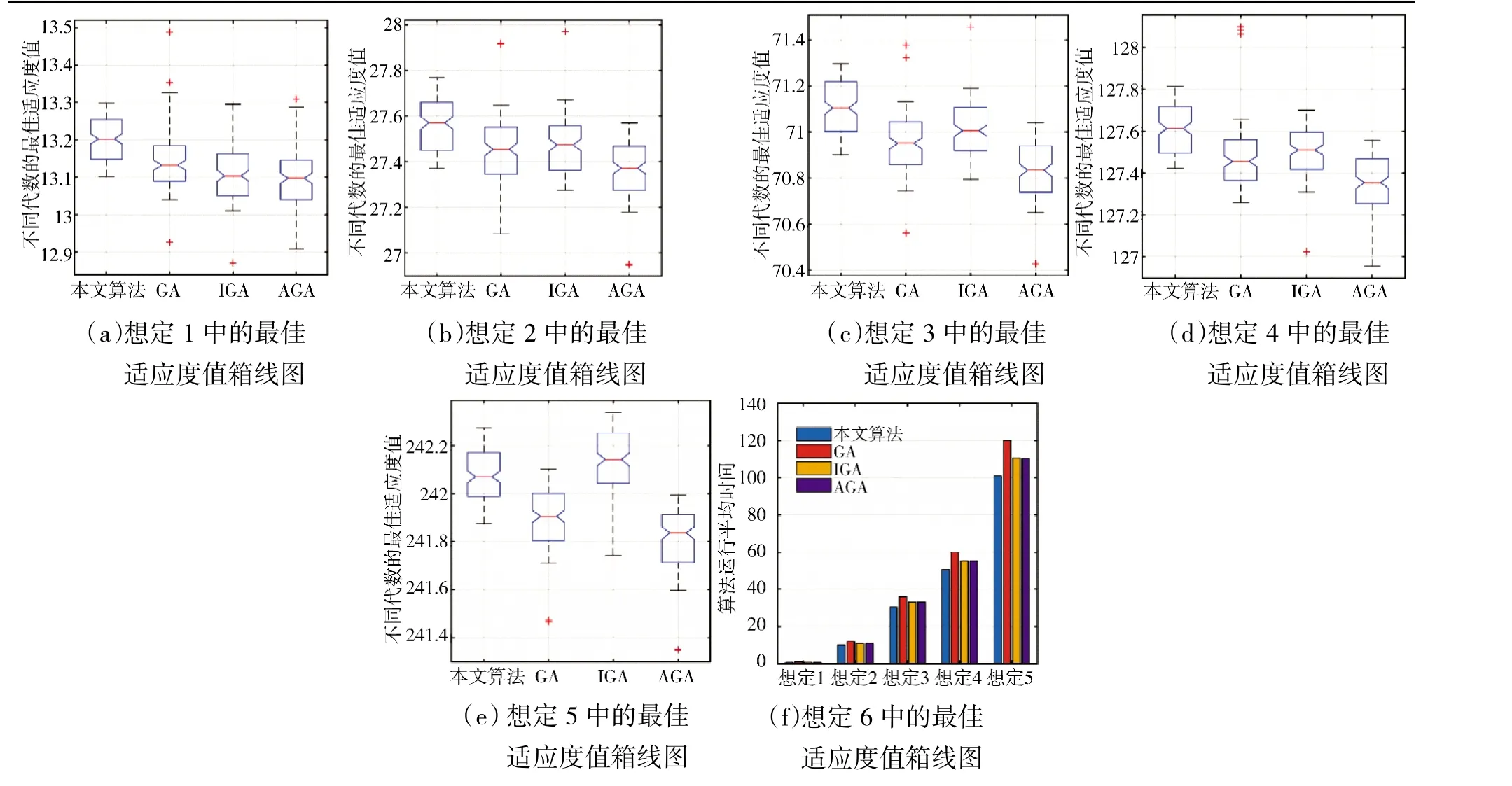
图6 算法运行仿真结果

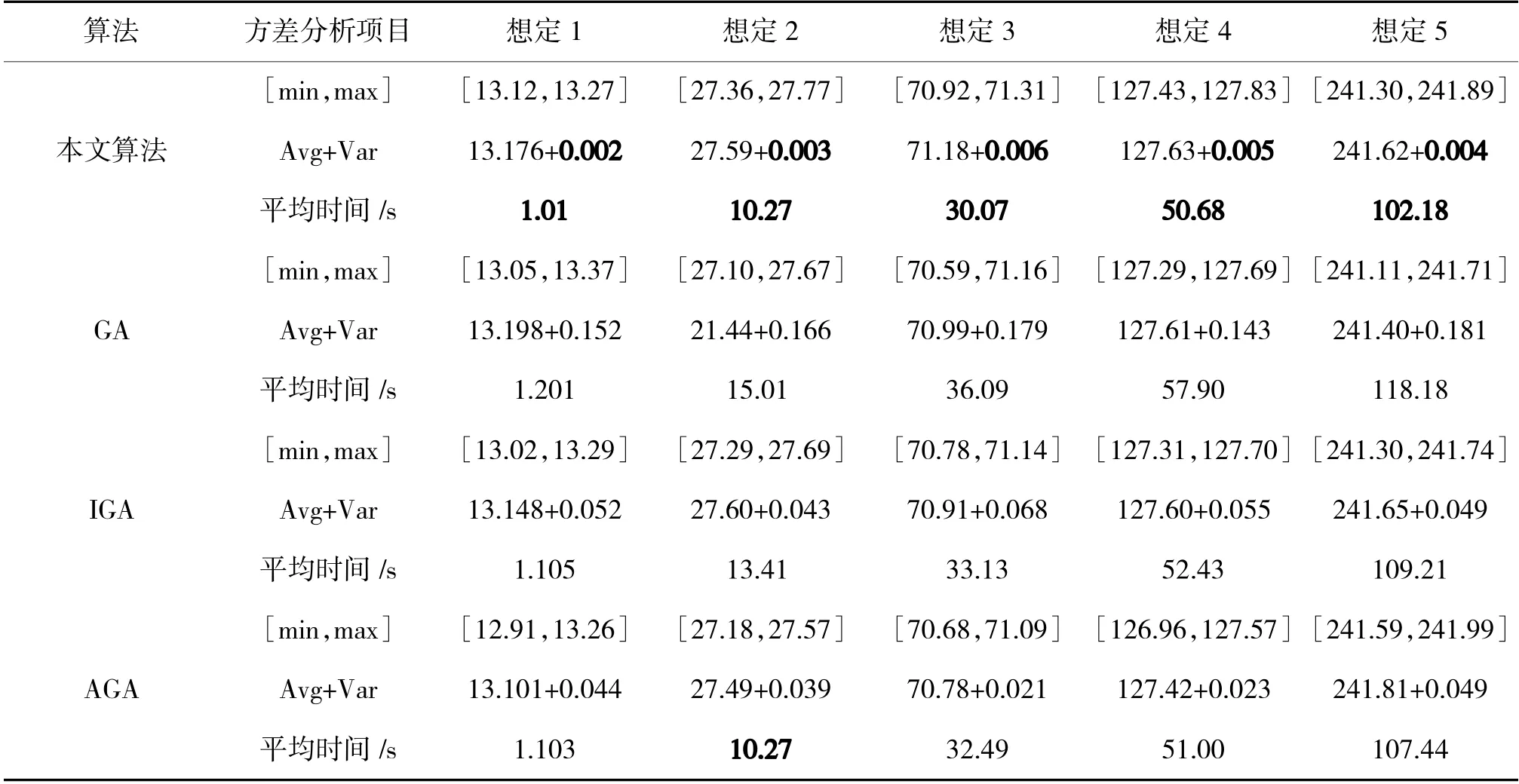
表4 仿真数据方差分析结果

表中共有3 个方差分析指标，分别为［最大值，最小值］、平均值+方差和算法平均运行时间。在每个想定下将方差和平均运行时间的最优值加粗表示，可以看出，本文构设的改进型混合遗传算法具有数据的绝对优势，在种群最佳适应度值达到稳定后波动很小，并且在进行遗传操作前将初始种群经过Lanchester 信息战模型的优化，使得每一代

的种群很快就能达到约束要求，算法运行时间也具有优势。

图6（a）～ 图6（e）是5 个想定条件下每代最佳适应度值的箱线图，反映出每个想定条件下每代最佳适应度值的方差关系；图6（f）是算法平均运行时间的柱状图，可以直观地看出对比的4 种算法之间的性能差异。通过以上对比说明，可以看出本文构设的改进型混合遗传算法能够有效解决电子对抗兵力规划问题，并且在同类型算法中性能较好。

5 结论

本文从作战指挥需求角度出发，通过作战筹划和作战实施过程的研究，对电子对抗运用提出具体需求，建立了电子对抗兵力的动态编成模型。在求解模型时将Lanchester 信息战模型运用到电子对抗兵力比的求解，进而优化了传统的遗传算法。通过合理设置5 个想定条件使用改进的算法对模型进行仿真求解，得到了电子对抗兵力编成结果，为直接指导作战指挥提供依据，并将本文算法与同类算法进行比较，说明了算法的可行性和优越性。在仿真实验过程中，仅通过计算机随机生成了一系列模型数据进行仿真，没有考虑实际作战过程中的适应性战场数据，为了解决这一问题，可以增加弹性作战知识库进行数据的自适应处理。下一步，要深入研究提出的问题，比如在具体作战实施中出现的兵力、环境和其余突发条件变化对模型带来的影响，求解模型时使用更加优越的算法等。