用于弹道组网测量布站评估的GDOP 拓展算法*
2022-07-25段鹏伟宫志华田家磊
段鹏伟,宫志华,岳 锐,田家磊
(解放军63861 部队,吉林 白城 137001)
0 引言
在武器系统试验靶场,获取高精度弹道参数是评定和分析武器打击精度的重要内容。随着测试设备的快速发展,多种设备组网的数据融合测量方式已经成为试验靶场的常规测量模式,在试前准备过程中构建更加科学的布站方案,已经成为提高目标测量精度的重要途径。很多学者对如何优化布站进行了深入研究,但其评估标准不尽相同。对于各项武器装备性能测试试验,已知目标的发射原点和方向、飞行速度以及理论轨迹等各种先验信息,在这些条件下,目标在理论轨迹上飞行的测量精度是评估布站方案优劣的标准。在各种定位系统中,几何精度因子(GDOP)常用来描述定位精度与布站几何的关系,因此,可以用GDOP 来评估布站方案。
GDOP 主要用于评估卫星与定位地点之间的几何关系的优劣,后来被引入到组网测量领域,以评估被测目标与测站形成的几何关系的优劣,但是对于组网测量,不同的数据融合的模型得出的GDOP 是不同的。受限于应用领域,很多学者在以等权重的多测距模型计算空间位置相对测站的GDOP,这种方法只考虑测站布站位置与空间形成的几何关系,没有考虑不同测站距离测元的测量精度是否相同。为了克服算法的应用缺陷,有的学者以不同精度作为权重的多测距模型计算GDOP,这种方法考虑了测元的精度指标,但是没有考虑测元的多样性。对于多种测元融合模型,主要有3 类GDOP 计算方法。第1 类是基于最大似然估计的GDOP 计算方法,简称最大似然法(ML),以不同精度的距离测元和角度测元获得了空间位置的GDOP,从而实现了更加精确的GDOP 求解。但是它的前提条件较为苛刻,很多时候无法满足,同时,对于有些测元无法求出其定位平面,这就导致虽然这些测元参与融合计算,但是无法给出其参与融合后的GDOP。第2 类是基于克拉美罗下界(CRLB)的GDOP 算法,简称克拉美罗法,这类算法可以拓展到任意测元,但是多数学者仍以距离测元和角度测元作为观测量,并且该算法需要已知所有测元与待估计状态量的联合概率密度分布函数,还要求测元的误差为相互独立的随机变量。第3 类是基于加权最小二乘估计的GDOP 计算方法,简称加权最小二乘法(WLS),以最小二乘法计算不同融合模型GDOP,没有约束条件,但是现有应用同样仅以距离和角度测元的融合模型计算GDOP,没有考虑其他测元是否对融合定位产生影响。
以上这些计算方法基本都是遍历空间的某些区域,逐个单点计算GDOP,因此,这些算法属于静态的GDOP 计算方法。在实际的弹道组网测量中,目标是运动的,目标定位的数据融合模型也是动态的,这时不仅静态的目标空间位置对布站方案的GDOP 有影响,动态的目标速度、加速度等与目标空间位置相关的参数也将参与到数据融合测量中,对目标定位精度产生影响,也可以认为对布站方案的GDOP 有影响。因此,本文以径向速度这一动态测元为例,将加权最小二乘法拓展到具有径向速度测元的动态融合模型中,使GDOP 能够更加准确地体现组网测量布站方案的优劣。
1 基于加权最小二乘估计的GDOP 拓展算法
弹道组网测量布站时,不仅可以获得目标的位置信息,还能够获得速度和加速度或者更多的先验信息。根据CRLB 计算过程中的Fisher 信息矩阵,增加与待估计状态量有关系的观测量数量,会降低CRLB,也就意味着提升了待估状态量的极限精度。以往算法仅仅利用了目标空间位置这些静态参数,而加权最小二乘法可以拓展到含有动态参数模型的GDOP 计算,属于动态的GDOP 计算方法。以含有径向速度测元的融合模型为例,将加权最小二乘法进行改进拓展。
1.1 建立误差模型
假定在组网测量系统中,第i 个测站的站址为(x,y,z),对目标测量值为距离测元R、方位测元A、俯仰测元E以及径向速度测元V一个或几个。不考虑站址误差时,对于空中位置为(x,y,z)的目标,由空间几何关系可得:

则可得到各测元对应的误差方程。
距离误差方程为:

方位误差方程为:

假定测量值中有i 个R,j 个A,k 个E,q 个V,则将全部测站的全部测元的误差方程联立,可用矩阵形式表示为:

1.2 GDOP 解算
根据加权最小二乘算法,可求得:

其中,P 为权系数矩阵,一般取测元误差的协方差矩阵。
弹道参数误差向量ΔX 的协方差矩阵为:
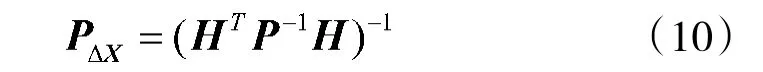
根据GDOP 定义,可得:

当各测元误差为互不相关的随机变量时,

该方法与以往的计算方法相比,模型的建立几乎不需要前提条件,不仅利用了雷达测量的距离测元和角度测元等静态测元,还利用了径向速度这个动态测元,而且还可以推广到更多类型的测元,极大限度地利用了测站的各种测元信息,计算得到的GDOP 能够更加切合实际数据融合结果。在各测元误差是互不相关的正态分布随机变量条件下,其结果即为克拉美罗下界,模型建立简单,拓展性强,适用范围广。
2 仿真分析
为了使仿真结果更加明了,静态GDOP 计算中仅使用距离测元,动态GDOP 计算中使用距离测元和径向速度测元。
2.1 加权最小二乘法与最大似然法比较仿真
在各测元误差是互不相关的正态分布随机变量条件下,加权最小二乘法与克拉美罗法等效,仅对加权最小二乘法与最大似然法做比较即可。
在相同布站方案和相同融合模型条件下,分别用最大似然法和加权最小二乘法计算相同区域的GDOP,以检验加权最小二乘法的正确性和准确性。
仿真条件:将4 个测站采用矩形布站,分别布设在(20 km,0,5 km),(20 km,0,-5 km),(-20 km,0,5 km),(-20 km,0,-5 km)这4 个高程为0 的点位上,采用4 测距融合模型,各测站测距精度为10 m,各测距误差是互不相关的正态分布随机变量。
用两种方法计算高度为10 km 的平面的GDOP等高线,如下页图1、图2 所示,图中*标记为测站点位。

图1 加权最小二乘计算GDOP 等高线图
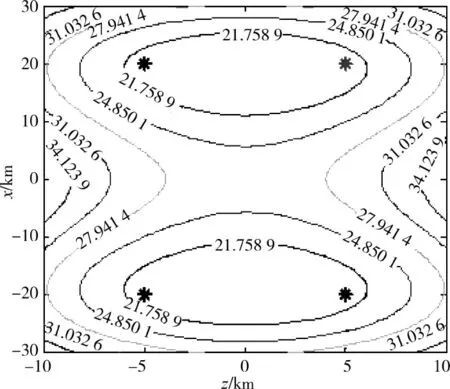
图2 最大似然法计算GDOP 等高线图
从GDOP 计算结果可以看出,在各测距误差是互不相关的正态分布随机变量的假定条件下,加权最小二乘法与最大似然法计算结果几乎完全相同,两种算法也是等效的。同时证明了3 种算法在假定条件下的等效性,验证了加权最小二乘法计算GDOP 的正确性、有效性和准确性。但是在各测元误差相关或者无法确定测元误差概率密度分布函数时,最大似然法和克拉美罗法无法计算GDOP,而加权最小二乘法不受假设条件限制。
2.2 弹道动态GDOP 仿真计算
在相同布站方案条件下,以加权最小二乘法及其拓展算法分别对空中弹道轨迹以不同的融合模型进行GDOP 计算,为了凸显径向速度的作用,模型尽量简化:以4 测距融合模型与4 测距4 测速融合模型进行对比仿真。
仿真条件:设计仿真弹道,包含时间、弹道三维坐标和速度等先验信息。以发射点为原点,发射方向为x 方向,竖直向上方向为y 方向,通过右手法则确定z方向。在这个坐标系下,将4 个测站采用常规的矩形布站,分别布设在(25 km,-4 m,-10 km),(120 km,-2 m,-10 km),(25 km,-3 m,10 km),(120 km,-5 m,-10 km)这4 个点位上。
以不同的测速精度进行两次仿真,各测站测距精度恒定为10 m,测速精度在两次仿真中分别设定为1 m/s 和0.1 m/s。
仿真弹道轨迹和布站方案示意图如图3 所示。图中曲线为弹道轨迹,以*标记了测站点位。

图3 仿真弹道轨迹与测站布站示意图
当各测站的测速精度设定为1 m/s 时,分别采用两种算法对弹道曲线的GDOP 计算结果分时显示,如图4 所示。
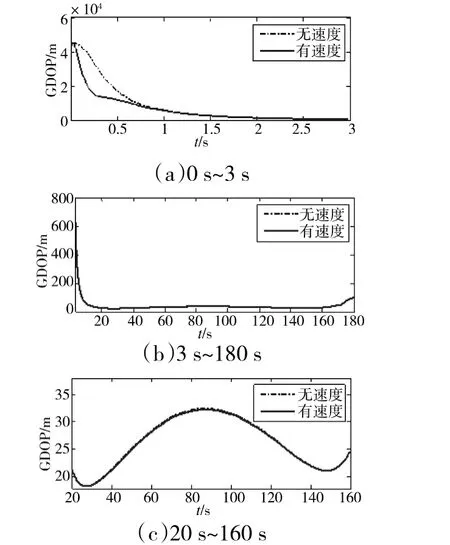
图4 两种算法的GDOP 计算结果(测速精度为1 m/s 时)
图4(c)为图4(b)放大后的弹道GDOP 计算结果曲线。
从图4(a)中可以看到,初始时刻由于目标与测站几乎在同一平面上,角度测元不参与融合时,GDOP 很大,意味着定位精度很低;但是含有径向速度测元的模型比没有径向速度的模型收敛要快一些。从图4(c)中可以看到,两条曲线基本重合,说明在各测站测速的相对精度较低时,虽然对GDOP 计算有影响,但是几乎可以忽略不计,也就是精度相对较低测元对融合定位精度的提升贡献很小。在这种条件下,两种算法对布站方案的评估结果相差不大,仅在弹道初始段稍有差别。
当各测站的测速精度设定为0.1 m/s 时,分别采用两种算法对弹道曲线的GDOP 计算结果如下页图5 所示。

图5 两种算法的GDOP 计算结果(测速精度为0.1 m/s 时)
从图5(a)中可以看到当测速精度提升,含有径向速度测元的模型计算的GDOP 收敛速度显著提高。从图5(c)中看到测速精度提升,GDOP 计算结果明显变小,融合定位后的精度也将更高。若测速精度进一步提高,GDOP 计算结果会变小,但是不会超过该融合模型的克拉美罗下界。因此,测元只要与关注的弹道参数有关联,就会对参数的测量精度产生影响,并且测元精度越高,GDOP 的计算结果越小,也就意味着融合精度越高。
在径向速度精度较高的条件下,两种算法对布站方案的评估结果相差比较明显,一是弹道初始段,两种方法的评价结果相差最大处相差超过一个数量级;二是在弹道中段,这时定位精度相对较高,但是两种方法的评价结果相差一倍左右。因此,经典加权最小二乘GDOP 算法在评估弹道组网测量的布站方案时未考虑动态参数,也同样具有一定的缺陷,本文提出的基于加权最小二乘的GDOP 拓展算法能够更加准确地评估布站方案。
3 结论
对于试验靶场现有的弹道组网测量模式,测站的布站方案对目标融合测量精度的影响较大,决定了对测站布站方案评估的研究具有重要的实际意义。本文在分析以往算法和经典的加权最小二乘GDOP 算法的优点和不足的基础上,以径向速度为例,将加权最小二乘法拓展到包含动态测元的模型中,提出了以基于加权最小二乘的GDOP 拓展算法计算结果为标准,对弹道组网测量布站进行评估的方法。
通过仿真分析,得到以下结论:
1)基于加权最小二乘的GDOP 拓展算法与以往的计算方法相比,模型的建立几乎不需要前提条件,只需测元数量冗余,因而可以利用更多动态测元,计算结果更加切合实际数据融合结果,能够更加准确地评估弹道组网测量布站方案。
2)在各测距误差是互不相关的正态分布随机变量的假定条件下,加权最小二乘法、最大似然法和克拉美罗法3 种方法等效,与3 种算法的理论基础相符合,验证了加权最小二乘法的正确性和准确性。
3)当测站与目标的几何关系较差时,包含更多动态测元的融合模型可以改善弹道的GDOP,且测元相对精度越高对融合结果精度影响越大,对组网测量布站评估的权重也越大。
本文提出的方法具有一定的应用推广价值,可以推广应用到组合导航定位、移动基站定位和水下声呐定位等其他定位测量系统的布站方案评估。
