低小慢目标拦截抗多径布儒斯特角弹道设计*

李 旭，叶继坤，唐 骁，李 炯

（空军工程大学，西安 710051）

0 引言

近年来，随着作战方式的进步与革新，以超低空巡航导弹、超轻型固定翼飞机、轻型直升机、滑翔机、低空无人机等为典型代表的低小慢新型对地打击武器进入了快速发展时期，特别是低空巡航导弹武器凭借其优秀的突防能力、出色的毁伤效能得到了世界军事强国越来越多的青睐，同时也成为了现行绝大多数防空体系的拦截难题。低小慢目标的主要特性有飞行高度低（10 m～100 m，最高不超过1 000 m）、雷达反射面小（RCS＜1 m）、飞行速度慢（一般在50 m/s 左右）。在低小慢目标的拦截过程中，导引头截获目标并实现对目标的稳定跟踪后，拦截弹转入末制导飞行，此时，真实目标回波和经地表反射的目标回波均落入导引头波束范围内，形成目标的多径效应，严重影响拦截弹的末制导精度。

目前，国内外学者主要从两个方面对低小慢目标拦截问题进行研究。一是分析低空目标对导引头雷达探测跟踪性能的影响，比如文献［2］中利用多路径回波模型，推导出低角目标的归一化场强，并定义了反映归一化场强起伏程度大小的场强波动因子，分析了各因素对雷达探测低空目标的影响权重，得到了利用短波雷达探测和增加天线的架设高度来对抗多径效应的雷达检测方法，但未从根本上解决低空目标的拦截难点；在文献［3］中基于多径散射模型在不同的外部电磁干扰环境下，分析推导了双门限检测器的检测性能，得到了雷达检测概率在多径环境下的表达式以及雷达信噪比的概率分布函数，通过仿真给出了短波雷达在多径环境下搜索跟踪低空目标的检测概率曲线（不同的双门限检测器在不同的虚警概率下），但未给出提高检测概率的具体措施。二是从改进制导律入手。如文献［4］中为了最大限度地减少杂波干扰，将弹目连线与水平面的夹角约束至布儒斯特角附近，基于FTSM 的设计思想，提出了一种非奇异FTSM 制导律，但实现该制导律的前提条件是需要知道准确的目标加速度，这无疑增加了技术难度；文献［5］中利用最优控制原理，结合线性二次型模型以及地海杂波的反射特性，设计出了一种能够有效对抗地杂波干扰和电磁干扰的最优导引律，并成功推导了特种弹道，但由于模型假设和简化过多，鲁棒性不佳。

低小慢目标拦截的最大困难在于多径与杂波的影响，而抗多径、杂波的根本途径就是变被动处理为主动抑制，其主要突破口之一就是采用布儒斯特角弹道。布儒斯特角弹道本质上是一个最佳角度问题，导引头按这个角度探测目标受到的多径干扰最小。本文以设计布儒斯特角弹道为出发点，在低小慢目标拦截末段使拦截弹的擦地角始终沿着布儒斯特角飞行，从而减小多径干扰对导引头探测目标的影响，使导引头能够准确跟踪、识别，并最终命中目标，其理想设计弹道如图1 所示。

图1 超低空目标拦截布儒斯特角理想弹道

1 具有布儒斯特角约束的弹目相对运动模型

为了简化弹-目运动方程，将末制导过程中的弹目相对运动解耦成俯仰平面和偏航平面两个分量的运动，如图2 所示。假设拦截弹速度和目标速度均为常量，且拦截弹速度大于目标速度；在攻击过程中攻角很小，则俯仰平面弹目运动方程为：

图2 拦截弹-目标相对运动关系

式中，V和V分别为拦截弹速度和目标速度；r 和r˙分别为拦截弹和目标相对距离与相对速度；θ和θ为拦截弹弹道倾角和目标弹道倾角；q 和q˙为拦截弹和目标之间的视线角和视线角速率；η和η为拦截弹前置角和目标前置角。

根据布儒斯特角的约束关系，拦截弹的擦地角必须时刻在布儒斯特角的约束范围内，因此，可得如图2 所示的弹目相对运动几何关系。图中，φ 为拦截弹的擦地角，该角度等于布儒斯特角。在图示ΔAMT 中，由正弦定理可得

则有

两边同时求微分，得

又因为

联合式（1）、式（2）、式（7）、式（8），可得

根据三角函数的二倍角公式可得

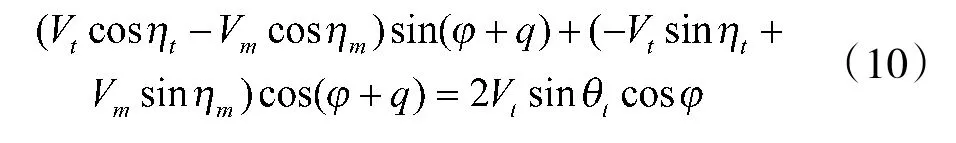
整理得

根据三角函数的两角和公式可得

联合式（3）、式（4）、式（12），可得

式（14）与式（1）～式（4）共同组成了超低空目标拦截抗多径布儒斯特角约束的弹目相对运动模型。

2 需用法向过载分析

根据需用法向过载的定义，有n=a/g，即需用法向过载等于法向加速度与重力加速度之比。拦截弹纵向平面的法向过载为n=Vθ˙/g，可见，通过分析拦截弹弹道倾角变化率θ˙的特性，即可得到法向过载的变化特性。

对式（14）求微分，即可得到拦截弹纵向平面的法向过载，令

有

两边同时求微分，得

其中

将式（18）代入式（17），可得拦截弹弹道倾角的变化率，有

可得

可见，拦截弹纵向平面的法向过载n与目标机动θ˙有关，在制导律设计时，应考虑目标机动对拦截弹道的影响。由于目标机动加速度不可测，因此，必须采用滤波算法或观测器等方法对目标的机动加速度进行估计。

3 扩张观测器设计

假设拦截弹在飞行过程中不发生滚转，将拦截弹在三维空间中的运动解耦成纵向平面运动和侧向平面运动。由于侧向平面的运动与纵向平面的运动类似，这里仅针对纵向平面拦截情况进行分析。纵向平面的弹目相对运动关系如图3 所示。图中V、V分别为拦截弹与目标的速度；a、a分别为拦截弹和目标的加速度矢量，θ、θ分别为拦截弹和目标的弹道倾角；r 为弹目相对距离；q 为弹目视线角；矢量i、j为惯性坐标系上的单位方向矢量。

图3 弹目相对运动关系

从而可以得到一阶不确定系统，即

其中，V为系统状态量；a为控制量；a为系统中的未知干扰；y 为系统的可测输出；若将a作为系统的扩张状态，则新系统为：

式中，g（t）是目标加速度的导数，a形式也是不确定的。当g（t）有界，即|g（t）|＜g时，可推导得到系统式（23）的二阶扩张观测器，即

4 布儒斯特角弹道的终止条件

拦截弹沿布儒斯特角弹道拦截目标，当弹目运动关系不再满足某些约束条件时，拦截弹将无法沿布儒斯特角弹道继续飞行，如图4 所示。拦截弹在轨迹点6 之前一直沿布儒斯特角弹道飞行；此后，如果继续沿布儒斯特角弹道飞行将导致拦截弹高度过低（甚至低于目标高度造成触地），拦截弹势必要拉高飞行，从而造成动力损失，且弹道需用过载变大，增加结构设计难度。因此，在轨迹点6（由弹目相对运动关系确定）之后，拦截弹将不再沿布儒斯特角弹道飞行。由于不再有布儒斯特角的约束，此时可采用修正比例导引等经典制导律。可见，拦截弹拦截低空目标并不能全程采用布儒斯特角弹道，在满足一定条件时必须由布儒斯特角约束制导律转为其他制导律。因此，需要计算分析拦截弹沿布儒斯特角弹道飞行的终止条件。终止条件取决两个因素：多径效应的影响和弹道需用过载。

图4 拦截弹的最小转弯半径

从弹道需用过载的角度考虑，BAC 制导律的终止及转其他制导律则越早越好；从多路径效应影响的角度考虑，BAC 制导律的终止及转其他制导律应越晚越好。因此，拦截弹沿布儒斯特角弹道飞行终止条件的确定需要综合考虑。

拦截弹纵向平面的法向过载为

可见，拦截弹纵向平面的法向过载与速度的平方成正比，与弹道的曲率半径成反比。要保证法向过载尽量小，在速度一定的情况下，弹道的曲率半径（即转弯半径）越大越好。如果限定拦截弹需用法向过载，则可得到拦截弹的最小转弯半径，如图5 所示，有

图5 拦截弹沿布儒斯特角弹道拦截目标的最小可分辨角

拦截弹沿布儒斯特角弹道拦截目标的最终目的是减小多路径效应对导引头跟踪识别目标的影响；拦截弹沿布儒斯特角弹道飞行，其真实目标、镜像目标与拦截弹的角度关系会随之增大；当该角度超过真实目标与镜像目标的最小可分辨角σ时，拦截弹导引头可以有效区分真实目标与镜像目标，从而削弱多路径效应对导引头跟踪识别目标的影响。

如图5 所示，根据正弦定理，有

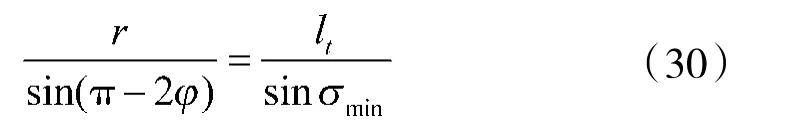
经整理，可得

即，当弹目距离小于r时，拦截弹导引头可以有效区分真实目标与镜像目标，从而可以终止BAC制导律。

综上，式（29）和式（31）就构成了约束BAC 制导律的终止及转其他制导律的条件。

5 仿真验证

以拦截战斧巡航导弹为例，假定战斧巡航导弹巡航高度为100 m，拦截区域地海杂波的布儒斯特角约为18°，仅考虑拦截弹的末制导拦截，且假定末制导的初始状态满足布儒斯特角约束关系，弹目相对运动关系如下：以拦截弹在地面的投影为坐标原点建立北天东惯性坐标系，仿真初始参数设计如表1 所示。

表1 BAC 制导律仿真参数

规定拦截弹的最大可用法向过载为40，最大可用横向过载为50，此外，在满足布儒斯特角弹道的终止条件后，末制导律由BAC 制导律转为经典比例导引律。针对巡航导弹做匀速直线运动、正弦型机动以及开关型机动3 种情况进行仿真分析。

5.1 情形1 来袭巡航导弹做匀速直线运动

假定来袭巡航导弹做匀速直线运动，按上述条件进行仿真可得来袭巡航导弹和拦截弹的三维弹道曲线、纵向平面交会曲线以及拦截弹的需用横向过载如图6～图8 所示。

由图6 可以看出在来袭巡航导弹不做机动时，拦截弹能够以较为平滑的弹道击中目标；从图7 纵向平面上的弹道投影来看，弹道十分平直，保证了拦截弹的机动能力，拦截弹的机动性能得到了充分体现和利用；从图8 可看出拦截弹的需用横向过载在允许范围内变化，变化趋势较为平缓，弹道比较容易实现，这是因为在制导律转换后，由于来袭巡航导弹不做机动，所以拦截弹不需要做转向机动或大角度抬头，需用过载变化不大。由仿真数据可得此时脱靶量为3.453 4 m，在大多数拦截弹的杀伤半径内，可以对巡航导弹造成有效杀伤。

图6 巡航导弹不机动时三维弹目交会曲线

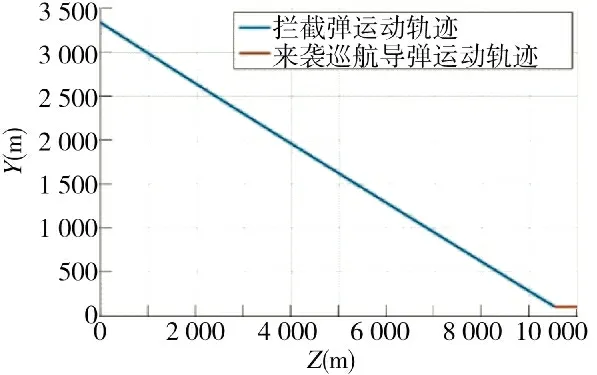
图7 巡航导弹不机动时纵向平面弹目交会曲线

图8 巡航导弹不机动时拦截弹需用横向过载

5.2 情形2 来袭巡航导弹做正弦型机动

假定来袭巡航导弹做变速运动，令其法向过载呈正弦函数变化趋势，nty=5·g·sin（0.02·i·ts）；横向过载亦按正弦函数变化趋势ntz=5·g·sin（0.02·i·ts）变化，其他条件不变，仿真结果如图9～图11 所示。

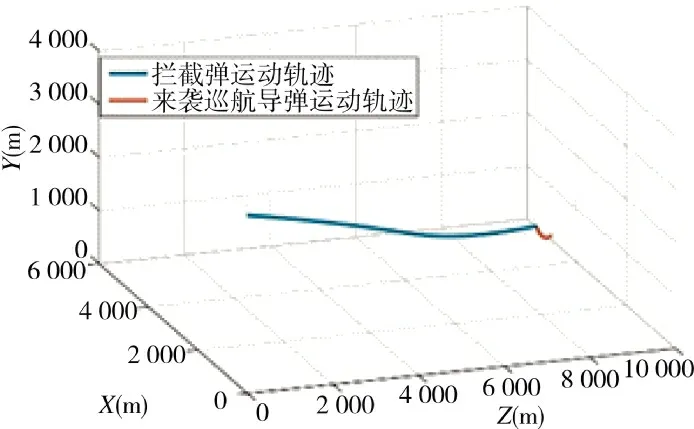
图9 巡航导弹机动时三维弹目交会曲线

图10 巡航导弹机动时纵向平面弹目交会曲线

图11 巡航导弹机动时拦截弹需用横向过载

由图9 和图10 可以看出，在来袭巡航导弹进行机动时，拦截弹仍能以较为平滑的弹道击中目标，拦截弹弹道有一定弯曲。但由于目标机动加速度较小，拦截弹没有发生大角度机动现象，所以弯曲程度在可接受范围内。从图11 可看出，拦截弹的需用横向过载在9 s 左右变化趋势由下降转为上升，这是因为在制导律转换后，由于来袭巡航导弹进行机动规避，拦截弹需要作出相应机动才能保证打击效果，需用过载会发生一定变化。由仿真数据得拦截弹的脱靶量为2.498 5 m，仍可对巡航导弹造成有效毁伤。

5.3 情形3 来袭巡航导弹做开关型机动

假定来袭巡航导弹做开关型机动，令其法向过载为nty=5·g·sign（sin（0.02·i·ts）），横向过载为ntz=5·g·sin（0.02·i·ts）变化，其他条件不变，仿真结果如图12～图14 所示。

图12 巡航导弹开关机动时三维弹目交会曲线

图13 巡航导弹开关机动时纵向平面弹目交会曲线

图14 巡航导弹开关机动时拦截弹需用横向过载

由图12 和图13 可以看出，在来袭巡航导弹做开关机动时，拦截弹按照BAC 制导律可以以平直弹道与目标交会，且由仿真数据可得此时的脱靶量为2.114 3 m，在杀伤半径内可以有效拦截巡航导弹；从图14 可以看出，由于来袭巡航导弹的大角度机动，导致拦截弹的需用过载也在上下波动，对拦截弹的机动性能提出了较高要求。

6 结论

本文立足于现有地空拦截武器制导体制和技术水平，瞄准未来武器装备发展需求，对拦截弹在导引飞行过程中为提高导引头抗干扰能力的关键飞行段实现布儒斯特角弹道的制导方法进行研究。设计了满足布儒斯特角约束的BAC 末制导律，对拦截弹需用过载进行了分析，设计了状态观测器来观测目标加速度，并进一步说明了布儒斯特角弹道的终止条件。仿真结果验证了所提低小慢目标拦截抗多径布儒斯特角弹道的有效性，为未来工程实践奠定了基础。