浙江省专升本高等数学考试向量代数与空间解析几何内容分析初探

金友良

（丽水职业技术学院，浙江 丽水 323000）

自从2005年起，浙江省全日制专升本考试试卷开始独立组卷，至今已有17年。通过全日制专升本统考统招，选拔优秀的高职应届毕业生到普通本科院校进行全日制两年制的继续深造，修完所有的规定课程，毕业时颁发普通高等本科院校的毕业证书和学士证书，这为高职院校优秀毕业生继续深造提供了一条快捷之路。

向量代数与空间解析几何是高等数学的一个重要组成部分，是学习多元函数微积分的基本，它通过坐标对空间曲线和空间曲面的性质进行运算和分析。这部分内容有在工程技术上有着广泛应用的向量及向量运算，然后利用向量为工具讨论空间的平面和直线，最后介绍空间曲面和空间曲线。考核向量代数与空间解析几何，每次有2个小题或1个计算题，小题题型要么是选择题，要么是填空题，分值一般在8分左右。本文对从2005年起至2021年浙江省专升本高等数学考试中向量代数与空间解析几何这部分考试题目进行了收集、归类和分析，整理总结出一定的规律，希望对有志参加全日制专升本考试的考生能起到一定的指导作用。

1 精细研读浙江省全日制专升本高等数学考试大纲，明确向量代数与空间解析几何内容的基本要求

（1）理解向量的概念，掌握向量的表示法，会求向量的模、非零向量的方向余弦和非零向量在轴上的投影。（2）掌握向量的线性运算（加法运算与数量乘法运算），会求向量的数量积与向量积。（3）会求两个非零向量的夹角，掌握两个非零向量平行、垂直的充分必要条件。（4）会求平面的点法式方程与一般式方程。会判定两个平面的位置关系。（5）会求点到平面的距离。（6）会求直线的点向式方程、一般式方程和参数式方程。会判定两条直线的位置关系。（7）会求点到直线的距离，两条异面直线之间的距离。（8）会判定直线与平面的位置关系。

2 分析历年向量代数与空间解析几何内容考试真题，筛查这部分内容考试热点

（1）求向量坐标。（2）向量运算。（3）两直线夹角题目。（4）直线与平面交点。（5）各种距离问题。（6）求平面方程。（7）求直线方程。

3 典型试题解析

3.1 求向量坐标

利用条件，先设所求向量的坐标，再根据条件求出坐标。

3.2 向量的运算

向量的运算有向量的线性运算，即加法运算与数量乘积运算，又有向量的数量积与向量积运算。

分析：直接利用向量积公式，以上可以求出

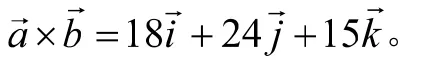
分析：利用向量运算的运算律，两向量垂直，数量积为0；同向量向量积为零向量，得：

3.3 求两直线的夹角

利用两直线方向向量的数量积，即可求出两直线的夹角。

3.4 求直线与平面的交点坐标

3.5 各种距离问题

3.5.1 两平行平面距离

先取出一个平面上的某一点，再用点到平面距离公式，即可求出两平行平面距离。

3.5.2 球面到平面之间的距离

这是求球面上的点到平面的最短距离。

3.5.3 异面直线之间距离

3.6 求平面方程

平面方程有点法式方程及一般式方程。

例10（2017年浙江省专升本考试计算题*22题）求过点且与直线平行的平面。

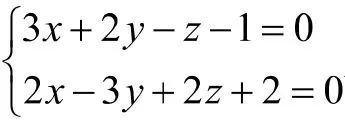
分析：由于已知直线是一般式方程，所以过此直线的平面束方程可以设为：

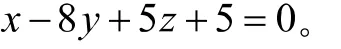
3.7 求直线方程

直线方程有点向式方程、参数方程及一般式方程。

例12（2007年浙江省专升本考试计算题*7题）求经过点且平行直线的直线方程。

分析：已知一点，关键求直线的方向向量。由题意，所求直线平行平面和平面，所以该直线的方向向量等于两平面法向量的向量积。

4 结语

通过上述分析，向量代数与空间解析几何考题不是很难，只要掌握考试大纲的基本要求，具有一定的空间想象力，尤其掌握向量的数量积、向量积、平面与直线的各种方式方程，就能很好地解决这部分内容的考题。