海洋大地电磁揭示了西太平洋苏达海山的电阻率结构
2022-07-23蔡晓仙吴招才
姜 杰,张 涛,蔡晓仙,吴招才
(1.山东科技大学测绘与空间信息学院,山东 青岛266000;2.自然资源部第二海洋研究所,浙江 杭州 310012;3.自然资源部海底科学重点实验室,浙江 杭州 310012)
0 引言
大地电磁法[1-2]采用天然电磁场作为场源,能反映不同深度范围的电阻率信息,是海底深部结构探测的主要手段。由于国外的技术封锁,我国海洋大地电磁的探测近几年才逐步兴起,成为海底探测的一个主要热点。国际上对海底火山的大地电磁探测与研究主要集中在洋中脊轴部火山区,并取得了对其深部电阻率结构的认识:高电导率地壳与软流层(5~50 Ω·m)由低阻岩石圈(50~100 Ω·m)连接,表明一小部分熔体从地幔的熔体源迁移到洋中脊轴部下的地壳岩浆室[3-4]。由于海洋板块内部火山(简称板内海山)形成于较老的岩石圈上,其岩浆深部侵入和喷出的方式及相应的结构都与洋中脊轴部火山不同[5]。目前对远离洋中脊的板内海山的电阻率结构还未见报道,需要进一步开展大地电磁探测工作以揭示其结构特征。
苏达海山位于马尔库斯-威克海山链,是典型的西太平洋板内海山。依托于“大洋号”科考船2020年的西太平洋海底精细地球物理调查航次,自然资源部第二海洋研究所用我国最新研制的大地电磁接收机对苏达海山进行了首次大地电磁测量。本次调查揭示了苏达海山的深部电阻率结构,对了解离轴板内海山的构建过程具有重要的意义。同时,由于苏达海山是我国锰结核的矿区,对其深部结构的了解也具有一定的资源意义。
1 地质背景及设备简介
2020年9月—11月在西太平洋苏达海山区域进行了海洋大地电磁的测量,实验区域及测点位置如 图1 所示。西太平洋区域发育了一系列的板内岩浆成因的海底山脉,包括马尔库斯-威克海山链、麦哲伦海山链和马绍尔海山链等。苏达海山位于马尔库斯-威克海山链北部,属于远离洋中脊的板内海山。

图1 测区地形图
近年来,我国大洋系列航次对苏达海山的部分区域进行了不规则的随船多波束测量,并进行了重力、磁力等地球物理调查和地质采样工作,但资料未见发表。KANEDA et al[5]利用OBS和多道地震资料揭示了位于苏达海山西侧的大型海山的地壳厚度可以超过15 km,岩浆侵入内核宽度小于30~40 km,内核与整体的体积比为15%~20%,表明大量的岩浆都通过喷发的形式释放,形成了内核周边的火山碎屑沉积物。马尔库斯-威克海山区内的海山沿NW—SE向散乱分布,整体形态并不呈现典型链状,且没有明确的年龄递进方向。前人使用40Ar/39Ar 定年法对马尔库斯-威克海山进行了定年[6-9],马尔库斯-威克海山的年龄范围在74~120 Ma之间,其中苏达海山南侧的拉蒙特海山的年龄为81.5~87.2 Ma。古地磁的研究也表明海山的形成过程没有明确规律[10]。这与夏威夷-皇帝海山链成因为典型地幔柱存在很大的不同。NATLAND et al[11]认为,包括岩石圈冷收缩、俯冲带拖曳、海山负载等5种应力的共同作用可能导致了古老岩石圈板块内的破裂,并使得地幔物质发生熔融并沿裂隙形成火山活动。
本次实验所用的仪器为OBEM-Ⅲ代海底大地电磁仪,是中国地质大学(北京)与广州海洋地质调查局联合研制的地球物理探测装备,装配2个电道、3个磁道,具有高可靠性、低噪声、大动态范围、低功耗、宽频带等优点[12-16],仪器参数见表1。
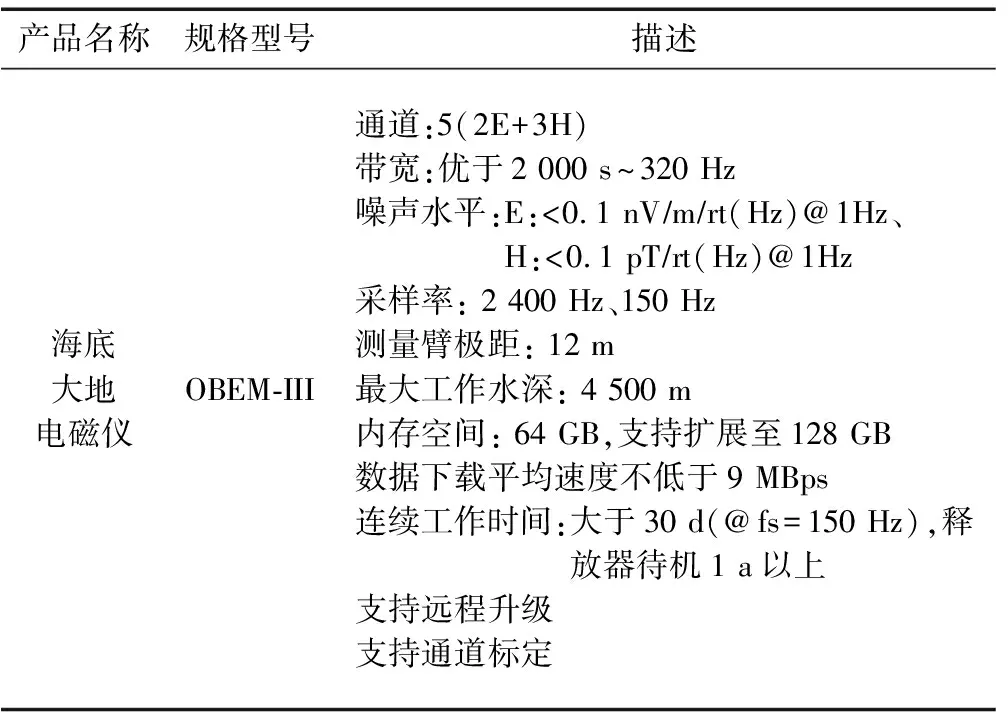
表1 OBEM Ⅲ仪器参数
2 数据处理及分析
大地电磁数据处理主要是将采集到的时间域序列数据转换为频率域序列数据,得到频率域序列数据之间的传递函数,最终获得高质量的阻抗张量、视电阻率和相位等参数的频率响应[17-19]。
海洋大地电磁数据处理的优势在于人为干扰所引起的电磁噪声影响较小,对人为噪音的处理可以忽略[20];但由于海底环境的复杂性、海水的“低通滤波”作用、海水运动等产生的电磁噪音等[21],也增加了海洋大地电磁数据处理的难度。
本文按照图2所示的数据处理流程,对海洋大地电磁接收机采集到的时间域原始数据进行处理。首先为时间域数据处理,包括时间域数据预处理以及时间域到频率域的转换。时间域数据预处理是指时间域数据的挑选、噪音的去除以及转换系数的校正;时间域到频率域的转换包括时间域数据时窗选择(根据目标频率)和时间域到频率域的转换。其次为频率域序列数据处理,包括选择目标频点,以目标频点为中心完成时窗内的数据叠加并进行时窗内的阻抗张量矩阵计算;进一步通过最小二乘或鲁棒(Robust)估计进行不同时窗阻抗张量矩阵的叠加得到阻抗张量矩阵[22-23];通过阻抗张量可以得到初步的视电阻率和相位曲线;最后,根据姿态棒记录的姿态数据对数据进行方位校正[20],得到最终的视电阻率和相位数据。
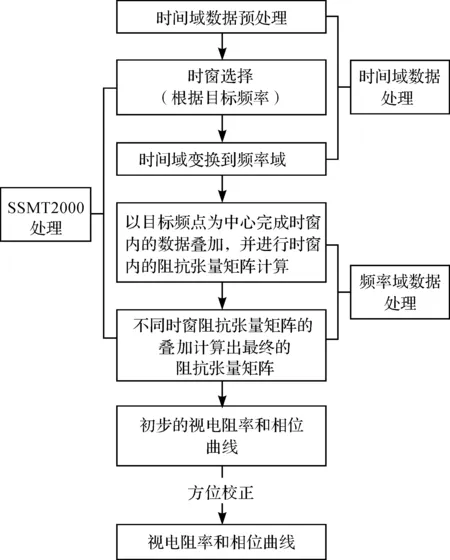
图2 海底大地电磁数据处理流程
2.1 数据预处理
图3a为测点的原始时间域数据,可看出Hx、Hy两个通道存在两种规律的周期性干扰信号,其分布特征分别为周期1 h、时长4 s以及周期6 h、时长2 s。这两种规律噪音是由于仪器读写数据产生的。对于这种周期和时长固定的干扰信号,在时间序列文件中手动定位首个噪音的初始时间,根据其周期和时长即可对干扰信号进行提取,进而实现信噪分离。按照这种信噪分离的思路,去除Hx、Hy两个通道中的规律噪音。随后按照下述原则选择数据:(1)曲线应具有很好的连续性,不连续的曲线,应去除凌乱、断档、飞点等数据;(2)Ex、Ey、Hx、Hy四个通道之间的数据曲线应具有良好的一致性。最终选择2020-10-01T18:58:07至2020-10-03T19:59:58区间(49 h)数据作为待处理数据。对选定数据进行衰减系数、极距和增益校正等预处理后的结果如图3b所示,数据曲线具有很好的连续性,各个通道间的曲线一致性良好。
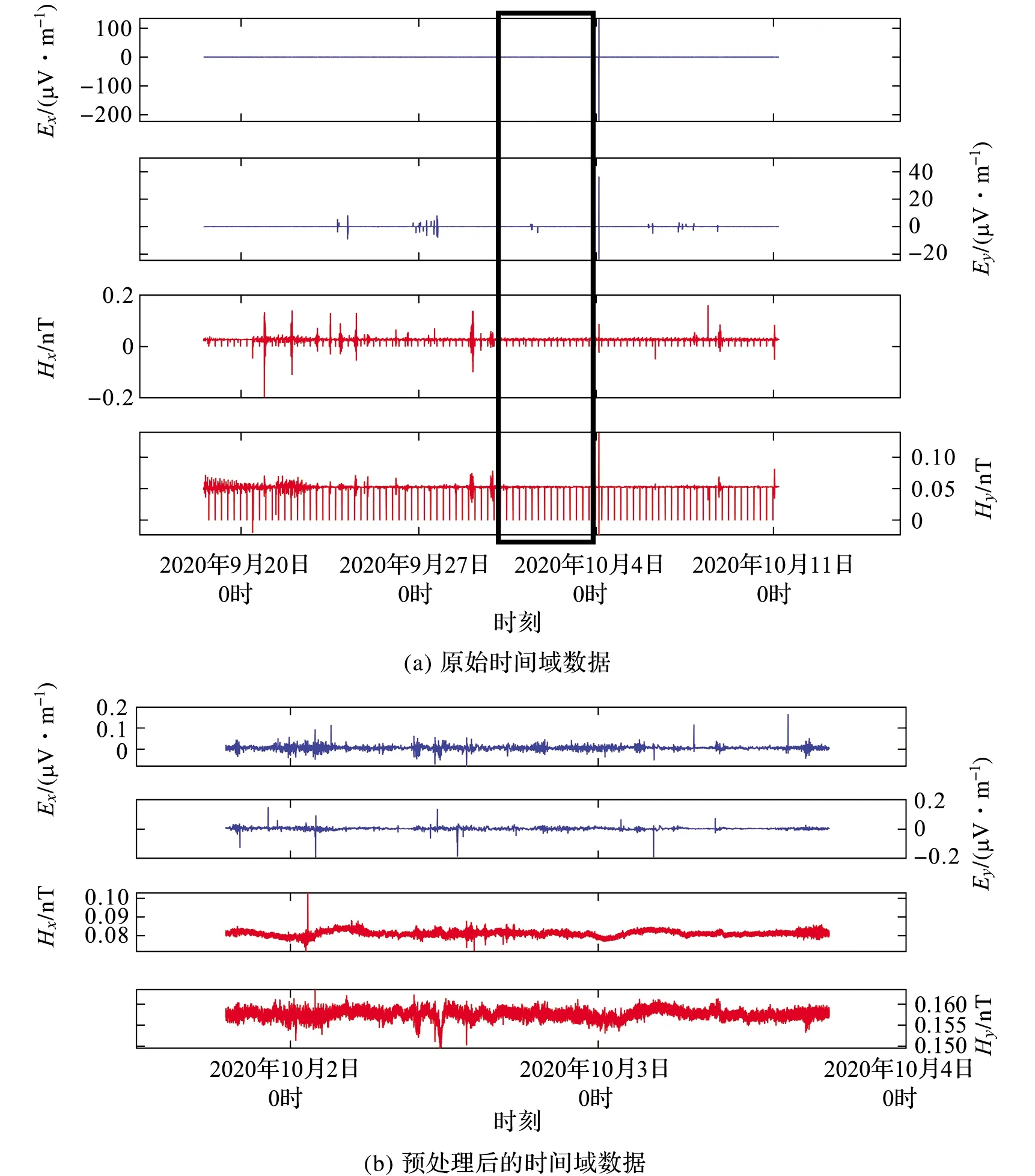
图3 时间域数据序列
2.2 数据处理
采用SSMT2000方法对预处理后的数据进行下一步处理。SSMT2000是加拿大凤凰地球物理公司生产的商用大地电磁处理软件,其时间域到频率域的转换采用传统的傅里叶变换方法[24],不同窗口的叠加采用鲁棒估算。鲁棒估算方法是根据观测误差的剩余功率谱大小对数据进行加权,突出未被干扰的数据,降低突变点数据的权,使突变点对阻抗估算值的影响最小,从而明显改善受电磁噪声污染的单站大地电磁资料[22-23,25-26]。此次处理具体采用的鲁棒估计形式为:比较电场和磁场的相干性,将相干性弱的去掉,去除各个通道的非相干噪音;权重方式为赋予磁场通道和电场通道之间一致性好的数据点更多的权重,可对数据进行更好的处理,降低误差棒的大小,使数据曲线更加光滑。
数据处理结果见图4。海水是良导体,具备“低通滤波器”的效应,能够压制测量数据的高频部分信号。假设海水的电阻率为0.3 Ω·m,根据趋肤定律,当站位水深为1 434 m,小于30 s周期的数据会被海水衰减掉,因此在后续数据处理和反演中去除小于30 s周期的短周期数据。

图4 SSMT2000方法处理结果
2.3 方位校正
海洋大地电磁测量在海底进行,仪器在海面释放,以自由姿态到达海底,因此测量方位是任意的。需要通过姿态棒记录的方位角θ对数据进行方位校正。按照公式(1),将阻抗张量Z旋转到磁北方向,旋转后的数据如图5所示。

图5 方位校正后的视电阻率(a)和相位(b)数据
(1)
式中:Zxx、Zxy、Zyx、Zyy为任意方位的阻抗张量;Zx′x′、Zx′y′、Zy′x′、Zy′y′为旋转后磁北方向的阻抗张量;θ为任意方位与磁北方向之间的夹角。
2.4 旋转不变量
大地电磁阻抗张量具有旋转不变的特性。目前研究表明,阻抗张量旋转不变量不受电性主轴的旋转和地形畸变等的影响,能够很好地解释三维构造特征[27]。本文采用两种旋转不变量,第一种为BERDICHEVSKY et al[28]提出的方案[公式(2)],通过平均有效电阻率(等效于由阻抗张量行列式导出的视电阻率),从畸变数据估计平均一维剖面模型,它能有效地协调复杂地点结构的方向特征。第二种为RUNG-ARUNWAN et al[29]提出的估算平均一维剖面模型的方法[公式(3)],该方法类似于使用BERDICHEVSKY et al[28]的平均值方法,但将旋转不变量定义为阻抗张量平方元素的和(ssq阻抗)。如图6所示,Zdet、Zssq的数据位于XY方向和YX方向数据范围内,并且两者基本一致,表明Zdet、Zssq数据是两个方向数据的综合。

图6 XY方向、YX方向、Zdet和Zssq的视电阻率(a)和相位(b)比较
(2)
(3)
3 数据一维正、反演结果及讨论
3.1 一维结构假设下MT响应测试
在一维反演前,需要先检验数据是否适合一维反演。采用Rho+算法对数据进行检验,该算法是对一维结构假设下MT响应函数一致性的测试[30],并通过设置视电阻率和相位的上下界限清除溢界值[31]。
对测点的XY方向、YX方向、Zdet、Zssq数据进行Rho+算法一致性测试,其结果如图7所示。除去高频段干扰后,4组视电阻率数据均与Rho+算法一致。相位数据方面,YX方向的一致性最好(图7b);Zdet和Zssq在80~140 s区间(图7c和7d),数据溢出较严重,其余数据一致性较好;XY方向(图7a)整体溢出较严重,与Rho+算法的一致性差。因此,采用对一维结构响应最好的YX方向数据进行一维反演。

图7 Rho+算法测试结果
3.2 反演模型及结果
反演采用OCCAM1DCSEM算法[31-34],针对反演的多解性,该算法通过正则化反演[30,34]确定与给定数据集兼容的电导率模型。在模型中,对应数据约束良好的特征被保留,而不受数据约束的特征将在模型中被平滑或者去掉[35-36]。
一维反演采用的模型如图8a所示:模型为各向同性;采用右手坐标系,Z轴垂直向下;从上到下分别为空气层、水层、海底以下的自由电阻率层。空气层为固定层,给定层宽10 km,电阻率1012Ω·m;水层为30层,层宽均匀分布,共1 434 m,每层海水电阻率值给定实际深度的电阻率值,避免海水层电阻率突变造成反演结果畸变[35],使用的海水电阻率值为太平洋圣选戈海槽区域的海水电阻率数据,为 OCCAM1DCSEM 算法程序包中自带的海水电阻率文件;海底以下的自由电阻率层为50层,从上到下层宽按对数分布,共100 km,允许数据的自由反演。对测点的YX方向数据进行一维反演的结果如图8b所示。海底下约2~3 km处存在电阻率突尖,可能反映出苏达海山表层沉积物较薄,电阻率较大的岩层接近海底面;海底向下15 km处电阻率最小,表明电阻率较大岩层下存在电阻率较小层;15 km以下电阻率逐渐变大,在 40~60 km处形成一电阻率高值,随后电阻率随着深度的增加而逐渐减小。这种变化特征符合地壳、地幔的电阻率分布特征:15 km以下的电阻率升高可以解释为地壳辉长岩向高电阻率的地幔橄榄岩的转换;60 km以下逐步降低的电阻率反映了橄榄岩电阻率随深度和温度的增加而逐渐变小。

图8 100 km反演模型及反演结果
实测数据周期最长可达到10 000 s(图5),对应趋肤定律计算的深度超过100 km。为进一步研究该地区的深部构造与岩石圈厚度,我们在保持其它参数不变的情况下,将反演模型加深到200 km(图9a)。结合图11可看出,在90 km以上的深度,2个模型的反演结果整体较为一致;90~110 km,电导率与深度之间的曲线斜率发生了显著转折,之后趋于稳定,我们由此推测此处为岩石圈-软流圈边界区域,即苏达海山的岩石圈厚度约为100 km。

图9 200 km反演模型的反演结果
3.3 苏达海山岩石圈结构讨论
为进一步确定海山的电阻率结构,本文结合YX方向反演结果与相关文献[5,37-39],建立理论电阻率结构模型,正演合成其数据后进行反演,并与YX方向反演结果对比,找出更相符的地下电阻率结构模型。
结合西北太平洋马尔库斯海山链的地震速度结构特征[5]、西南太平洋Tūranganui海山的电性结构特征[37],通过多次试验,得到最佳模型如下:海底至 5 km 深度为电阻率100 Ω·m的玄武岩层;5~13 km为火山碎屑岩层,电阻率为20 Ω·m; 13~18 km为火山碎屑岩层,电阻率为3 Ω·m; 18~23 km为辉长岩层,电阻率为300 Ω·m;结合MATSUNO et al[38-39]对马里亚纳区域一维深部地下电性结构的研究,给定23~100 km为橄榄岩层,电阻率为 1 000 Ω·m;100 km以下电阻率设为1 Ω·m(图10a)。模型的反演结果与观测值较为符合,可以复现海底下的电阻率突尖、15 km 左右的电阻率最小值、40~60 km间形成的电阻率高值(图10b和图11)。因此,3.5 km 厚的玄武岩层、13 km厚的火山碎屑岩以及5 km厚的辉长岩,可以解释苏达海山的观测电阻率。在15 km处电阻率值大于实测数据反演值以及在40~60 km处电阻率值小于实测数据反演值,说明实测数据反演结果可能存在过度拟合的情况。
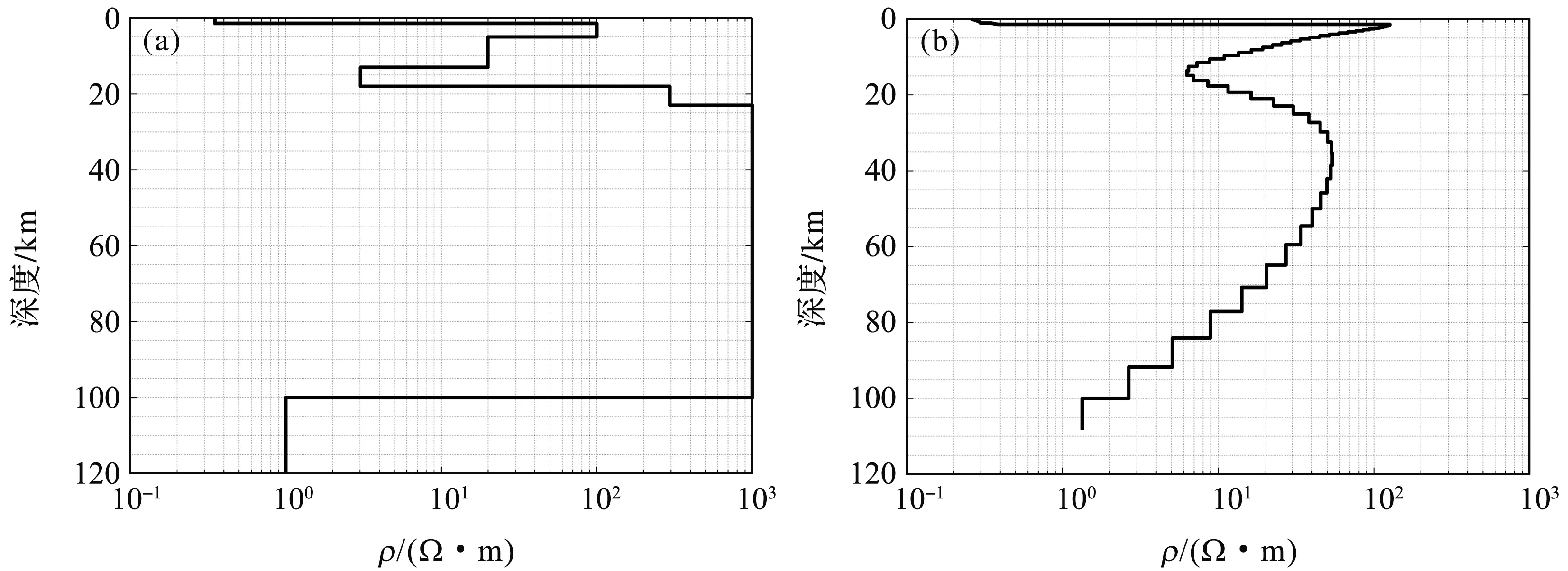
图10 最佳模型(a)与其对应的反演响应曲线(b)
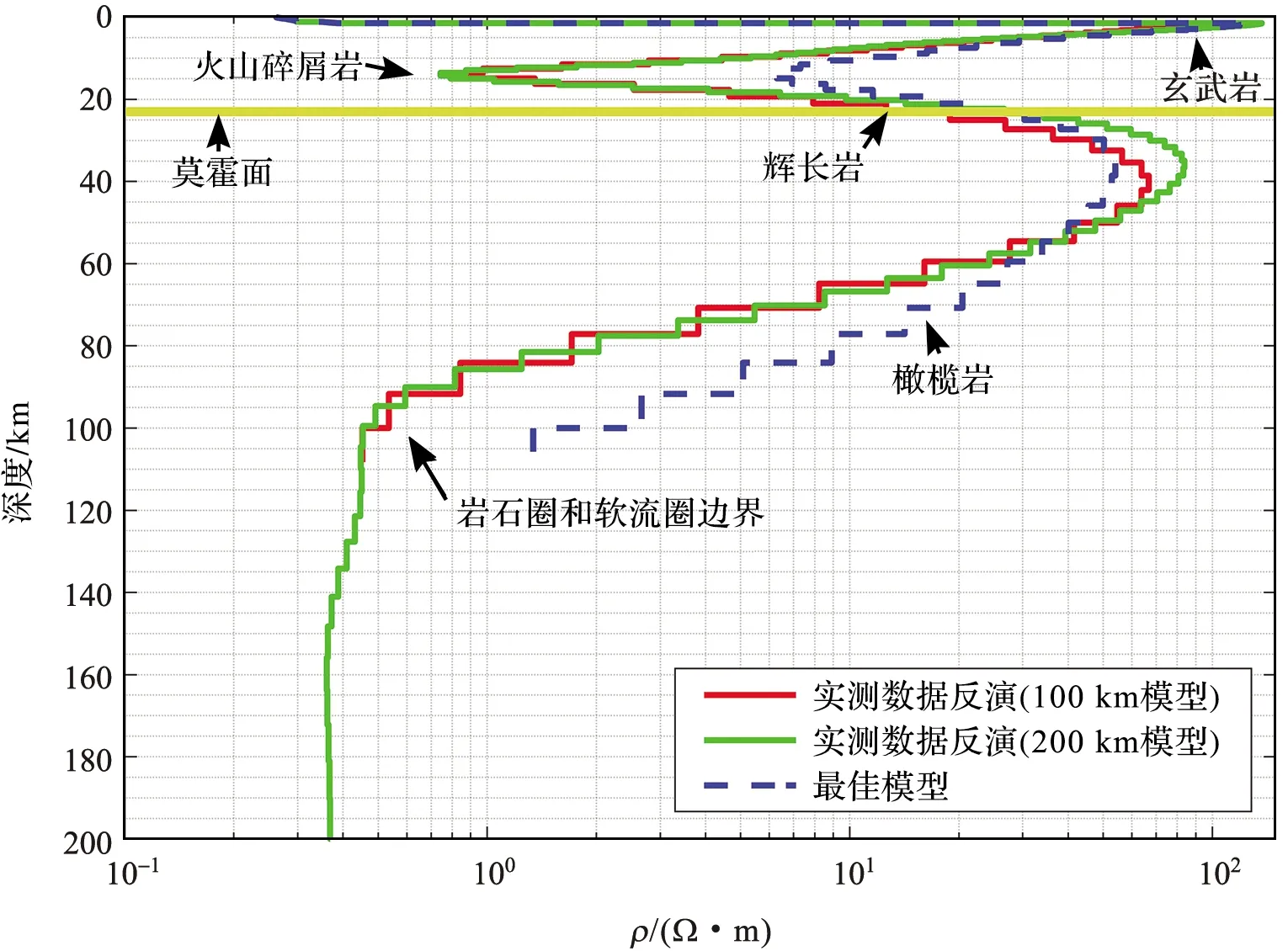
图11 反演结果对比图
苏达海山的平均水深为1 500 m,周边深海盆为 5 000 m,假定周边深海盆为洋壳,平均厚度为6 km,洋壳密度为2.8 g/cm3,地幔密度为3.3 g/cm3。基于艾里地壳均衡模型,苏达海山的地壳厚度约为 22 km,这与本文用电磁数据推断的21.5 km的地壳厚度较为一致。苏达海山较厚的火山碎屑岩说明其喷发部分占了主体,这可能与苏达海山喷发时的水深较浅、喷发压力较小有关,也可能是由于苏达海山的岩浆挥发性比较强,更易于喷发。同时,苏达海山的结构与马尔库斯-威克海山链上小规模火山的地震推断的地壳结构类似[5],表明这种小型海山的形成可能都具有以喷发性为主、侵入性较弱的模式。
4 结论
本文首次对板内海底火山——苏达海山的海洋大地电磁调查数据进行了处理,对旋转后的数据以及旋转不变量进行了一维反演,进一步通过一维正演来推断苏达海山的岩石圈结构。苏达海山的电阻率模型表明:海山表层覆盖着薄玄武岩层,厚度在 3.5 km 左右;薄玄武岩层下是低电阻率的火山碎屑岩,厚度为13 km左右;其下为5 km厚的辉长岩层。通过大地电磁数据推断的苏达海山地壳厚度约为 21.5 km,与艾里地壳均衡模型推断的22 km的地壳厚度相符。苏达海山较厚的火山碎屑岩层表明其喷发部分为主体,与地震推断的马尔库斯-威克海山链上小规模火山的地壳结构类似。
致谢感谢自然资源部第二海洋研究所2020年西太平洋海底精细地球物理调查航次的船长杨江志在数据采集过程中提供的帮助;感谢中国地质大学(北京)陈凯博士及其团队在仪器及数据预处理方面的指导;感谢自然资源部第二海洋研究所秦林江博士、南方科技大学赵云生博士在数据处理及正、反演方面提供的帮助;感谢山东科技大学赵俐红博士提供的浪潮TS10K集群的算力支持;感谢山东科技大学王飞燕博士在反演算法上的指导。
