权重不平衡有向网络下的分布式优化算法
2022-07-23夏俊,倪伟
夏 俊,倪 伟
(南昌大学数学系,江西 南昌 330031)
分布式优化系统是近几十年来的一个热门研究领域,在社会科学和工程等领域已有广泛的应用,如分布式电源配电网[1]、无线传感器网络[2]等。分布式优化主要是通过多智能体和邻居之间进行信息交流从而实现全局网络的最优决策,目前在相关方面已取得大量的研究成果。
分布式优化问题的早期工作主要是迭代离散时间算法,比如,Nedic等基于一致机制设计的分布式次梯度投影算法[3],以及Jakovetic和Xavier基于梯度提出的加速分布式算法[4]。Nedic和Duchi分别提出了分布式梯度下降算法[5]和分布式对偶平均算法[6],但是在算法[5-6]中使用了递减步长,其收敛速度会随着步长的减小而变慢。为了克服递减步长导致分布式优化算法收敛速度变慢这一问题,Yuan和Matei设计了固定步长的分布式优化算法[7-8]。虽然固定步长要比递减步长算法的收敛速度快,但文献[7-8]中提出的算法只能收敛到最优解的某一个邻域,因此,其不能获得精确的最优解。为了设计一个固定步长且能精确收敛到最优解的分布式优化算法,我们将梯度跟踪和比例积分策略[9]相结合,通过设计辅助变量跟踪梯度的平均值,从而避免了使用递减步长也使得算法能够精确收敛到问题的最优解。
目前,大部分分布式优化算法都是针对无向图网络提出的,对于有向图网络特别是权重不平衡有向网络获得的结果相对较少。在无向图网络下进行的分布式优化算法包括众所周知的分布式梯度下降算法[10],精确的一阶算法[11]以及镜面下降算法[12]。然而当通信网络是有向图时,算法[11-12]就不能收敛到优化问题的最优解。为了在有向网络下也能解决优化问题,Gharesifard和Kai分别提出了基于梯度的分布式优化算法[13]和离散时间的分布式自适应算法[14],另外,Lee和Ribeiro提出了基于鞍点动力学的分布式算法[15]。但是算法[13-15]都是在权重平衡的有向图网络下提出的,事实上,基于权重不平衡有向图的分布式优化算法在收敛性的分析上与无向图本质上没有很大区别,且权重平衡这一条件在一般有向图下不易达成。因此,将连续时间的分布式优化算法推广到权重不平衡的有向图具有重要意义和挑战。之所以在权重不平衡有向图网络下的分布式算法设计比较困难,是因为权重不平衡有向图对应的拉普拉斯矩阵是非对称的,而且在算法收敛性分析中不易选择合适的李雅普诺夫(Lyapunov)函数。于是,Nedic和Olshevsky基于push-sum在有向图网络下提出了一个离散时间的分布式优化算法[16]。此外,Li和Ding在权重不平衡有向图下提出了一个连续时间的分布式自适应优化算法[17]并且证明了其收敛到优化问题的最优解。但不足之处是分布式优化算法[17]直接用到了拉普拉斯矩阵零特征值的左特征向量,若不能提前获得拉普拉斯矩阵零特征值的左特征向量这一信息,则该算法就无法收敛到问题的最优解。为了解决这一问题,我们通过设计变量对拉普拉斯矩阵零特征值的左特征向量进行跟踪,从而提出了一种全新的连续时间分布式优化算法。
总而言之,在权重不平衡有向网络下,我们基于梯度跟踪[5]和比例积分策略[9]在连续时间下设计了一个固定步长的分布式优化算法。本文所设计算法的收敛速度不受递减步长影响,而且在通信网络是权重不平衡有向图且不能提前知道拉普拉斯矩阵零特征值的左特征向量这一信息的情况下也能解决多智能体系统的优化问题。之后选取适当的Lyapunov函数并结合凸分析理论证明了本文所提出的分布式优化算法能精确收敛到优化问题的最优解。
本文其余部分安排如下。第1节包含符号说明和数学理论,并提出分布式凸优化问题。在第2节中,在权重不平衡有向图下提出一个连续时间分布式优化算法,并分析其平衡点和收敛性。最后一节给出简要的总结和未来的工作。
1 预备知识
1.1 符号说明
1.2 代数图论
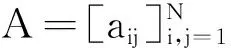
1.3 问题描述
我们考虑一个由N个智能体组成的网络系统,它们之间的通信网络由权重不平衡有向图G来描述。对于每个个体i∈…,N},令fi(x):n→是其局部成本函数,仅个体i和它的邻居j∈Ni知道fi(x)的信息。网络上的全局成本函数定义为这个网络的目标是解决优化问题
(1)
假设1有向图网络G是强连通的。
假设2对所有的i=1,2,…N,局部成本函数fi(x)强凸。且对某些li>0,其梯度∇fi(·)是li-Lipschitz连续的,即‖∇fi(x)-∇fi(y)‖≤li‖x-y‖,∀x,y∈n。
(2)
其中X=col(x1,x2,…,xN)∈nN,L∈N×N是通信图G对应的拉普拉斯矩阵。
本文将在权重不平衡有向图下设计连续时间的分布式优化算法来解决问题(1),即解决分布式优化问题(2),在下一节中将给出具体的算法。
2 权重不平衡有向图下的分布式优化算法
本节首先在权重不平衡有向图下设计一个连续时间的固定步长分布式优化算法,然后对所设计算法的平衡点和收敛性进行分析。现考虑一组个体I=1,2,…,N在通信网络是权重不平衡有向图的情况下解决优化问题(1),对于i∈I,实施如下分布式算法:
其中a、b是有待确定的正参数,vi∈N是辅助变量,vii是vi的第i个元素,且vi的初值满足
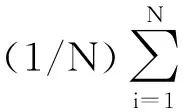
引理1[17]设L∈N×N是强连通有向图G对应的拉普拉斯矩阵,则有如下性质成立:
(1) 矩阵L有一个简单零特征值对应于右特征向量1N。且所有的零特征值都有正实部。

引理2[19]对于系统(3d),存在ε0>0使得ε0≤vii(t)≤1成立,对任意的i∈{1,2,…,N}和t≥0。
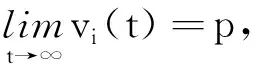
为了方便后续平衡点和收敛性的分析,设=L⊗In,D=d⊗In∈nN×nN,其中N×N,将算法(4)写成紧凑的形式如下:
(4)
其中X=col(x1,…,xN),Y=col(y1,…,yN),Z=col(z1,…,zN)∈nN,V=col(v1,…,vN)∈NN,G(X)=col(∇f1(x1),…,∇fN(xN))∈nN,且N=L⊗IN。
首先分析分布式优化算法(4)的平衡点,有如下引理。
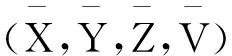
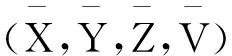
(5)
(7)
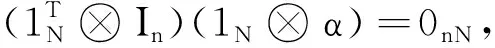
(8)
同样的在式(8)两边同时左乘p⊗In可得
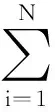
接下来这个定理分析了分布式优化算法(4)的收敛性,从而证明了该算法能够在权重不平衡有向网络下收敛到优化问题(1)的最优解。
定理1若假设1和假设2成立,个体间的通信由权重不平衡有向图G表示,且L是有向图G对应的拉普拉斯矩阵。对任意初始值X(0),Y(0),Z(0)∈nN,以及初值V(0)=col(v1(0),…,vN(0))∈NN,其中参数a和b分别满足如下不等式:
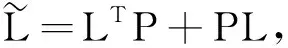
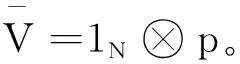
(9)
其中
接下来分析系统
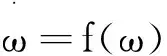
(10)
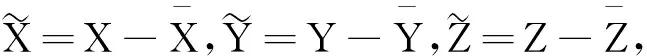
(11)
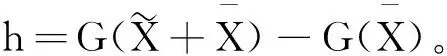
则V1关于式(11)的导数为
(12)
由Young不等式,可得如下不等式:
(13)
(14)
由Young不等式和∇fi(xi)的Lipschitz连续性,i=1,2,…,N。可得不等式
(15)
同理可得:
(16)
由Young不等式并结合0 (17) (18) (19) (20) 故,当 本文主要在权重不平衡有向网络下用分布式的方法解决了优化问题,通过梯度跟踪方法与比例积分策略相结合提出了一个连续时间分布式优化算法。通过设计变量对拉普拉斯矩阵零特征值的左特征向量进行跟踪,将分布式优化算法从无向图推广到了权重不平衡有向图。我们所设计的分布式优化算法是固定步长且没有直接用到拉普拉斯矩阵零特征值的左特征向量这一信息,并对其收敛性进行了分析,证明了该算法在权重不平衡有向网络下能精确收敛到优化问题的最优解。在之后的研究中,可以通过跟踪拉普拉斯矩阵零特征值的左特征向量这一方法将更多的分布式优化算法推广到权重不平衡有向网络,还可以与分布式博弈相结合,将其推广到有向网络。
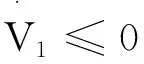
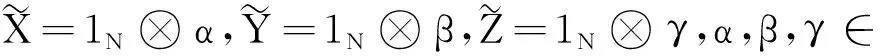
3 结论
