一维可压缩黏性辐射反应气体方程组强解的整体存在性
2022-07-23帅清清韩小敏
帅清清,韩小敏,王 滕*
(1.南昌大学数学系,江西 南昌 330031;2.南昌航空大学数学与信息科学学院,江西 南昌 330063)
1 引言与研究背景
一维空间上的可压缩黏性辐射反应气体方程组在Lagrange坐标下表示如下[1-2]
vt=ux
(1.1)
(1.2)
(1.3)
(1.4)
其中(x,t)∈×[0,+∞),(x,t)分别表示Lagrange空间坐标和时间变量;未知函数v(x,t)>0、u(x,t)、θ(x,t)>0、z(x,t)、e(x,t)>0和P分别表示气体的比容、速度、温度、反应物浓度、内能和压力;常数d>0和λ>0分别为物质扩散系数、反应物和生成物的热差系数;μ>0和κ>0分别表示黏性系数和热传导系数;反应速率函数φ=φ(θ)满足如下Arrhenius定律(见文献[1-2]):
(1.5)
其中正常数K和A分别是反应速率系数和活化能系数,b为非负常数。
将辐射当作连续场,高温辐射使液体处于热平衡状态,由Stefan-Boltzmann辐射定理知,压力P和内能e分别满足如下状态方程:
(1.6)
其中R、Cv和a分别是理想气体常数、比热和Stefan-Boltzmann常数。考虑黏性系数μ和热传导系数κ满足如下关系式:
(1.7)
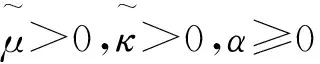
对方程组(1.1)-(1.7),考虑如下初始条件:
(v(0,x),u(0,x),θ(0,x),z(0,x))=(v0(x),u0(x),θ0(x),z0(x)),x∈
(1.8)
和无穷远处的渐近性态:
(1.9)
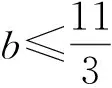
κ(v,θ)=κ1+κ2vθb
其中κ1,κ2和b为正常数。对于具有一般形式(1.7)的黏性系数μ和热传导系数κ,可压缩黏性辐射反应方程组光滑解的整体适定性问题有待进一步讨论。
对于热传导系数为温度的幂函数的情形,本文建立了一维全空间上可压缩黏性辐射反应气体方程组柯西问题大初值强解的整体存在性,主要结果如下:
a)定理1.1 假设α=0,β≥0,0≤b≤min{15,8+β},如果初值(v0(x),u0(x),θ0(x),z0(x))满足
(v0-1,u0,θ0-1)∈H1(),z0∈H1()∩L1(),

则问题(1.1)-(1.9)存在唯一的整体强解(v,u,θ,z),且对任意T>0有
(1.10)
注:定理1.1推广并改进了现有的若干结果:一方面,将文献[13]关于Navier-Stokes方程的结果推广到了含有反应方程的情形,并得到了类似的结论;另一方面,将文献[11]的结果推广到了更一般的具有退化的热传导系数情形。
2 定理1.1的证明
首先给出问题(1.1)-(1.9)强解的局部存在性结果,其证明见文献[14-16]。
引理2.1在定理1.1 的假设下,存在T*>0,使得问题(1.1)-(1.9)在×[0,T*]上有唯一的强解(v,u,θ,z)满足(1.10)。
为了完成定理1.1的证明,下面将建立光滑解的整体估计,进而可以将解的局部存在时间延续到任意时刻,从而得到整体解的存在性。
首先,给出如下基本能量估计。
引理2.2在定理1.1的假设下,对任意0≤t≤T有
(2.1)
(2.2)
(2.3)
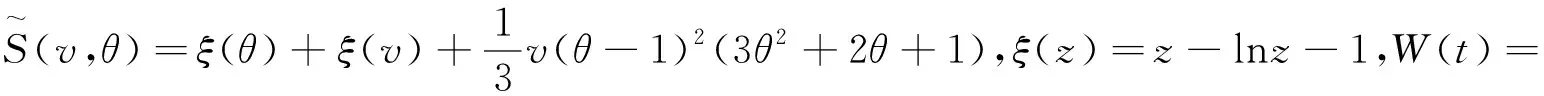
证明对(1.4)关于(x,t)在[0,t]×上积分可得,
联立(1.9)可得(2.1)成立。
在方程(1.4)两边同乘z,再关于(x,t)在[0,t]×上积分,联立(1.9)即可得(2.2)成立。
利用(1.1),(1.2)和(1.5),可将(1.3)改写为如下形式
(2.4)
在方程(1.1)和(1.2)两边分别乘以(1-v-1)和u,在(2.4)两边同乘(1-θ-1),将它们所得的结果相加可得
对上式关于(x,t)在[0,t]×上积分,再联立(1.9)可知(2.3)成立,引理2.2证毕。
类似于文献[17]的方法,可得如下z(x,t)的上下界估计:
引理2.3在定理1.1的假设下,对所有(x,t)∈×[0,T]有
0≤z(x,t)≤1
(2.5)
注意到文献[13]中关于v的上下界估计并不涉及到方程(1.3)和(1.4),从而可以根据文献[13]的结果直接给出如下估计。
引理2.4在定理1.1的假设下,对所有(x,t)∈×[0,T]有
C-1≤v(x,t)≤C
(2.6)
下面,我们将证明温度θ的下界。
引理2.5存在一个正常数C使得对于所有的(x,t)∈×[0,T]有
θ(x,t)≥C-1
(2.7)
证明记
(θ>2)(t)={x∈从(2.3)可得
从而对任意t∈[0,T]有
(2.8)
对任意的p≥0,在(2.4)两边同乘θ-5wp(其中w≜(θ-1-2)+),然后关于x在上积分,联合(2.6)和(2.8)可得
(2.9)
对上式运用Gronwall不等式可知
(2.10)
从而
(2.11)
注意到上式中的正常数C和p无关,在(2.11)上取极限p→∞可得
由上式可得(2.7),引理2.5证毕。
下面,我们给出ux的L2(×(0,T))范数估计。
引理2.6存在正常数C使得如下估计成立
(2.12)
证明在方程(1.2)两边同乘u,然后关于x在上积分可得
(2.13)
这里用到了(2.3)、(2.6)和如下估计
(2.14)
为处理(2.13)右边的两项,直接计算可得
(2.15)
联立(2.14)、(2.3)、(2.6)和(2.7)有
(2.16)
该式结合(2.6)、(2.3)和(2.14)可得
(2.17)
对(2.13)关于时间积分,结合 (2.16)和(2.17)即得(2.12),引理2.6证毕。
下面,我们给出ux和vx的L∞(0,T;L2)估计。
引理2.7存在正常数C使得
(2.18)
证明注意到
由此可将(1.2)重写为
(2.19)
(2.20)
由(2.3)、(2.6)和(2.7)可得
(2.21)
对(2.20)关于(x,t)在×[0,T]上积分,并利用(2.6)、(2.12)、(2.7)和(2.21)可得
(2.22)
注意到
该式联立(2.22)和(2.6)可得
(2.23)
分部积分结合(1.1)可得
(2.24)
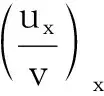
(2.25)
其中上式最后一个不等式用到了以下估计:
(2.26)
对(2.25)两边在[0,T]上积分,并利用(2.6)和(2.12)可得
(2.27)
利用(2.21)和(2.7)可有以下估计:
(2.28)
上式联立(2.23)和(2.27)可得
(2.29)
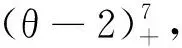
由0≤b≤β+8和如下估计
(2.30)
我们有
(2.31)
由(2.26)可得(2.31)右端第一项的如下估计
(2.32)
上式最后一个不等式用到了如下估计
(2.33)
将(2.32)代入(2.31)中,取η充分小,结合(2.6)、(2.7)和(2.12)可得
(2.34)
将(2.34)两边同乘C2=C1+1,将其结果和(2.28)相加,并选择适当小的ε可知
(2.35)
上式结合(2.12)、(2.16)以及Gronwall不等式可得
该式联合(2.6)可得(2.18)成立,引理2.7证毕。
下面,我们给出zx的L∞(0,T;L2)估计和zxx的L2(0,T;L2)估计。
引理2.8存在正常数C使得
(2.36)
证明将(1.4)重写为
(2.37)
在上式两边同乘zxx并在上积分可得
(2.38)
由(2.18)可得
(2.39)
另外,利用(2.18)可知对任意0≤b≤15有
从而有
(2.40)
对(2.38)两边关于t在[0,T]上积分,联立(2.39)、(2.40)、(2.2)、(2.4)、(2.16)以及(2.7),通过选择适当小的ε可得
(2.41)
由(2.2)、(2.37)、(2.40)和(2.41)可得
上式结合(2.41)即得(2.36),引理2.8证毕。
最后,我们给出θ的高阶导数估计,进而可以得到θ的上界估计。
引理2.9存在正常数C使
(2.42)
证明由分部积分和(1.1)可知
在(2.4)两边同乘θβθt后在上积分,类似文献[13]的估计方法,并利用上式可得
(2.43)
其中用到了(2.6)、(2.7)、(2.18)、(2.26)以及利用(2.8)、(2.7)和(2.31)所得到的如下估计:
和
(2.44)
利用(2.18)和(2.6)可得
(2.45)
因此,联合(2.43)、(2.45)、(2.18)和(2.36)可知,对任意0≤b≤15有
(2.46)
该式结合(2.44)可知,对任意(x,t)∈×[0,T]有
θ≤C
(2.47)
由(2.7)和(2.46)可知
(2.48)
最后,由(1.3)可得
该式结合(2.6)、(2.7)、(2.47)、(2.48)、(2.26)、(2.40)、(2.16)和(2.18)可得
联立(2.48)即得(2.42),引理2.9证毕。
