提升空间中渐近平均跟踪性和链回归点的研究

冀占江，贝彩霞，张更容

(1.梧州学院大数据与软件工程学院，广西高校图像处理与智能信息系统重点实验室，广西高校行业软件技术重点实验室，广西 梧州 543002；2.梧州职业学院卫生健康学院，广西 梧州 543002；3.湖南第一师范学院数学与计算科学学院，湖南 长沙 410205)

0 引言

研究n维环面等特殊流形上动力学性质时最常用的方法就是提升系统，因此一个系统与它的提升系统的动力学性质是否一致就成为研究的热点[13-14].考虑到渐近平均跟踪性和链回归点具有较高的应用价值且它们在提升空间中的研究成果较少，本文选择在提升空间中研究它们的动力学性质，所得结论弥补了提升空间中渐近平均跟踪性和链回归点理论的缺失.

1 预备知识

定义1 设X，Y是拓扑空间.称f是一个同胚映射，如果f：X→Y是一一映射且f和f-1都是连续的.

定义2[15]设(X，d1)和(Y，d2)是度量空间，f：X→Y是一一映射.称f是等距映射，如果对任意的x，y∈X，有d2(f(x)，f(y))=d1(x，y).

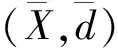
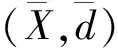
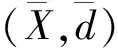
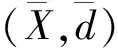
定义7[16]设J⊂N.称J是密度零集，如果

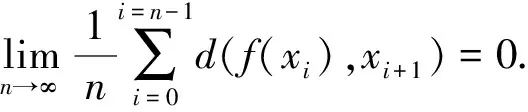
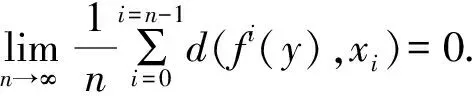
定义10 设(X，d)是度量空间，f：X→X连续.称f具有渐近平均跟踪性，如果{xi}i≥0是X中f的任意渐近平均伪轨，存在y∈X使得y渐近平均跟踪{xi}i≥0.

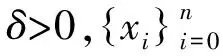
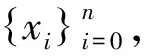
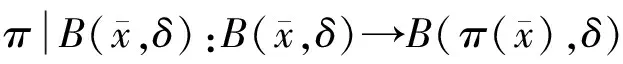
是等距同胚映射.

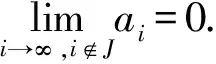
2 主要定理及证明

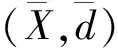
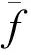
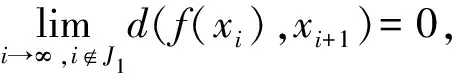
d(f(xi)，xi+1)<ε.

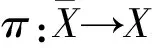
再由引理1可知，

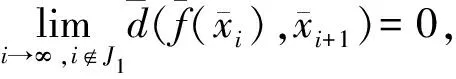
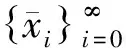
由引理2知，存在密度零集J2使

故∃N2∈N+，当i≥N2且i∉J2时，有

(1)

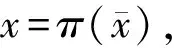
是等距映射，故

根据(1)式，当i≥N2且i∉J2时，有

d(fi(x)，xi)<ε.

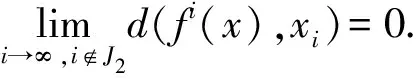
则f具有渐近平均跟踪性.

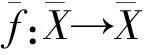
(2)

由引理2，存在密度零集J3使

故∃N3∈+，当i≥N3且i∉J3时，有

(3)

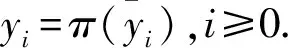
由(3)式，当i≥N3且i∉J3时，有

d(f(yi)，yi+1)<η.

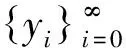
d(fi(y)，yi)<η.

(4)

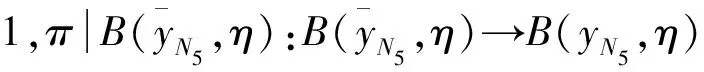
由(4)式可知，

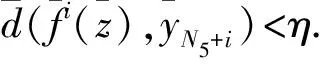
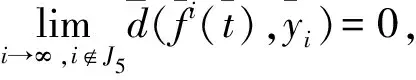
(5)

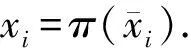
是等距映射，故

由(5)式有

d(f(xi)，xi+1)<ε.

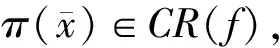
3 总结